前の記事
機械学習は平行四辺形を予測できるか?(1)外挿ってできるかな?
前の記事を書いて思ったのですが、あまりプログラムテクニックが書いてありませんでした。でも、一応pyhtonで計算しているので、タグはpythonにしてあります。pythonで機械学習している人も多いだろうから、qiitaへの投稿でも良いですよね。。。
この計算は、scikit-learnで計算しています。
さて、前の記事で外挿ができないことはわかりました。
じゃぁ、次のような問題は、どうなるでしょうか?
問3:小さい値と大きい値で学習して、その間は予測できるか?
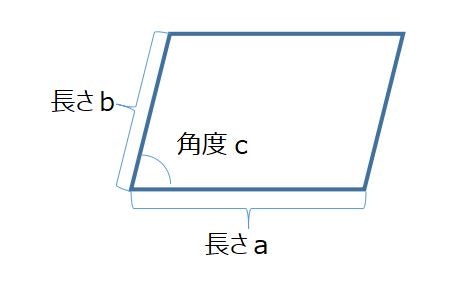
| a | b | 角度c | |
|---|---|---|---|
| 学習用 | 0~50 and 1000~1100 | 0~100 | 0~90 |
| 内挿?外挿? | 150~900 | 50 | 45 |
簡単な問題です。底辺の長さaを0~50、1000~1100で予測して、その間の150~900は予測ができるのでしょうか?
線形回帰のLassoは、たぶん予測できるのでしょう。でもランダムフォレストやニューラルネットワークは、どうなるのでしょうか?
このデータセットがあったら、0~1100まで予想できると、ついつい思ってしまいます。現実のデータは、こういう例がありそうです。
結果です。
まず、学習の結果の決定係数とグラフです。
| 決定係数 | 学習 | テスト |
|---|---|---|
| Lasso回帰 | 0.686 | 0.661 |
| ランダムフォレスト | 0.999 | 0.975 |
| ニューラルネットワーク | 0.997 | 0.997 |
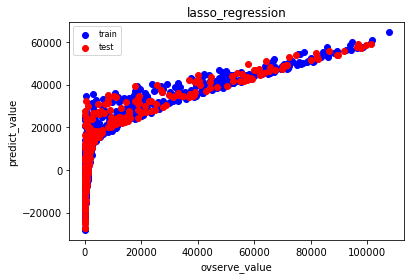
| Lasso | ||
 |
||
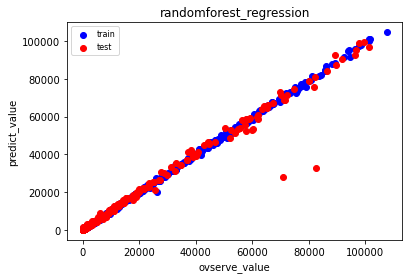
| ランダムフォレスト | ||
 |
||
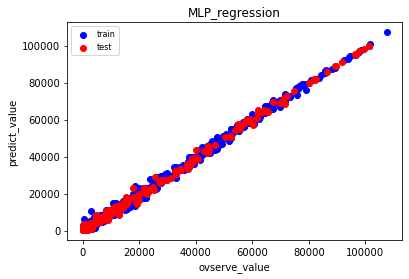
| ニューラルネットワーク | ||
 |
||
| 底辺aの値は、小さい値と大きい値にしてありますが、bと角度cがランダムに作られているため、面積のareaの領域はつながって見えます。 |
グラフで見ると、ランダムフォレストの2つのはずれ値がなぜ出たのかはわかりませんが、でも、これらのグラフと決定係数をみれば、Lassoを選ぶ必要はないと感じてしまいますし、ランダムフォレスト最高!ニューラルネットワーク最高!って思いますよね。
では、底辺aで学習した間の値を予測するとどうなるか?です。
とりあえずグラフを見てみましょう。
Lasso
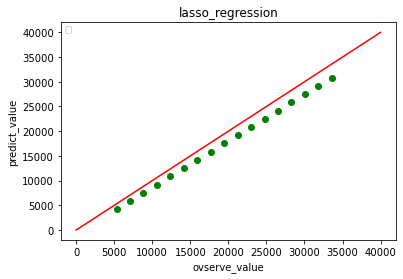
ランダムフォレスト
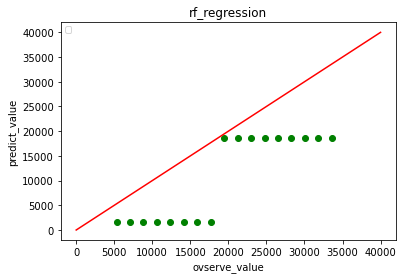
ニューラルネットワーク
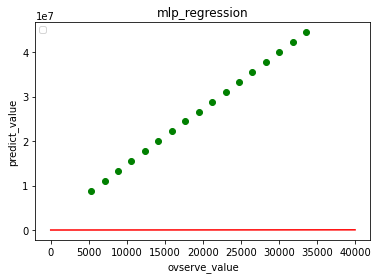
底辺aの数値を学習の間に入れていますが、ニューラルネットワークは全然ダメです。これを見ると、ディープラーニングでの回帰予測は、しっかり内挿で予測しないと危ないですね。
ランダムフォレストもそうです。内挿、外挿をしっかり見極めないといけません。
Lassoは、みてわかるように、近い値で予測できています。少しでも外挿の恐れがある場合は、線形回帰が良いということかもしれません。
結論
機械学習で外挿の予想はやめましょう。特に、内挿のように見える外挿が要注意です。少しで外挿の予想をしていると思ったら、線形であると仮定を立て、線形回帰で頑張りましょう。
ということかもしれません。
次は、記述子設計を検討してみます。