機械学習って外挿できるのか?
兵庫県マテリアルズ・インフォマティクス講演会(第4回)講演2「記述子設計手法」で兵庫県立大学高度産業科学技術研究所の藤井先生が、記述子の設計について講演をされていました。ランク落ちのところがまだ少し理解ができていませんが、とても良い講演だったと思います。勉強になりました。
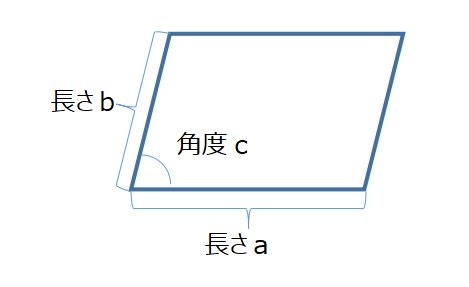
講演の途中に三角形の例があって、なるほどと思ったので、ちょっと平行四辺形を例に遊んでみました。
問題:平行四辺形の面積を2辺の長さと2辺の間の角度の3つの特徴量が与えられた時に、面積を予測できるか?また外挿は可能か?
まず、次の図形の平行四辺形の面積を出すために、2辺の長さと2辺の間の角度をランダムに1000個作成しました。辺の長さは100~1000の間、角度は90度以下です。
高校の数学くらいで考えると、平行四辺形の面積の公式は、底辺と高さをかければ出ることがわかっていますが、高さがわからないので、三角関数をつかって、高さを求めます。
height = b*sin(c)
高さが求まったら、それに底辺をかけます。
\begin{align}
area &= height*a\\
&=b*sin(c)*a
\end{align}
仰々しく書きましたが、まぁ、高校の数学レベルですので、簡単ですね。
これで、3つの特徴量(長さa,b、角度c)と目的変数の面積(area)のデータセットが出来ました。
ここで問題です。
問1.平行四辺形は機械学習できるでしょうか?また精度は?
問2.機械学習の結果から、外挿はできるでしょうか?辺の長さの学習で計算した外の数値が与えられた時に、予測できるでしょうか?
問2は、当然、機械学習だから外挿はできないはずですが、どんな感じになるか、示したものが意外とないので、計算してみました。平行四辺形くらいなら外挿できるのでしょうか?
問1.平行四辺形は機械学習できるでしょうか?また精度は?
3つの機械学習をつかってみました。
・LASSO回帰
・ランダムフォレスト
・ニューラルネットワーク
いずれもscikit-learnを使用しています。LASSOを使っているのは、後で記述子設計で特徴量を増やして特徴量選択して遊ぶために、特徴量が少ないですが、Lasooで計算しています。
ちなみにLassoのαは1、ニューラルネットワーク(MLP)の隠れ層は100で計算してみました・
結果です。決定係数は、こんな感じになりました。
| 決定係数 | 学習 | テスト |
|---|---|---|
| Lasso回帰 | 0.796 | 0.778 |
| ランダムフォレスト | 0.998 | 0.989 |
| ニューラルネットワーク | 0.919 | 0.913 |
これを見るとランダムフォレストがよくて、次にニューラルネットワークが良いように見えますが、グラフを見るとどうでしょうか?
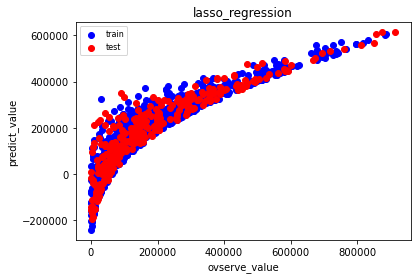
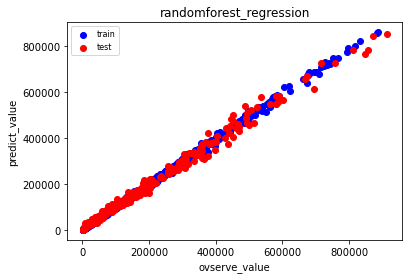
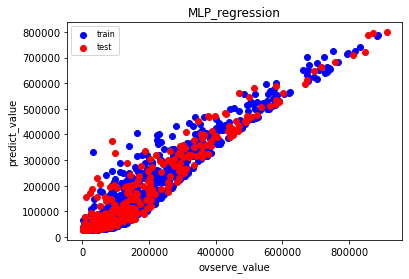
ランダムフォレストはきれいに予測できました。ニューラルネットワーク(MLP)も少しひろがっていますが、これもよく予測できています。Lasso回帰では、数値が大きい方はよく予測できていますが、小さい方は予測が広がっています。
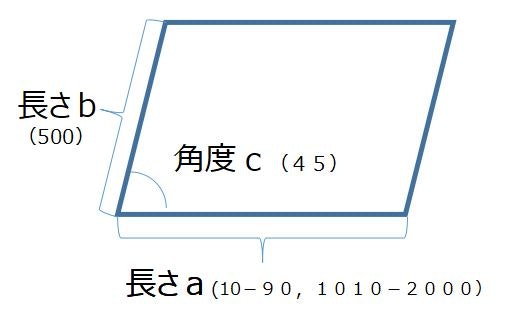
問2.機械学習の結果から、外挿はできるでしょうか?辺の長さの学習で計算した外の数値が与えられた時に、予測できるでしょうか?
この学習器を使って、数値の小さい領域と大きい領域は果たして予測可能でしょうか?
||a |b |角度c|
|---| -------------- | ---------- |---------- |--|
|学習用|100~1000|100~1000|0~90|ランダムに1000個作成|
|外挿下側検討用|10~90 |500|45|b,cを固定|
|外挿上限検討用|1010~2000 |500|45|b,cを固定|
これでどうなるでしょうか?
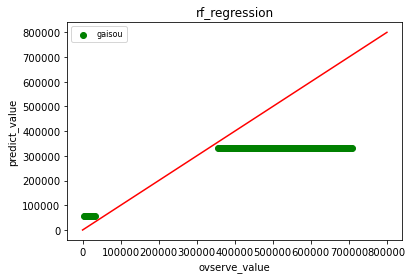
bとcは、内挿で、aのみ外挿です。一つだけならなんとかなるでしょうか?

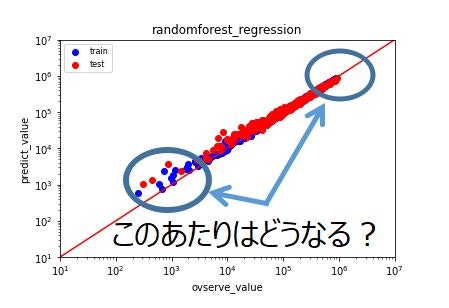
赤い線が対角線ですが、ランダムフォレストもニューラルネットワークも少しの外挿でも全然予測ができません。ニューラルネットワークなんか、見当違いの数値になっています。なんともなりませんでしたね。
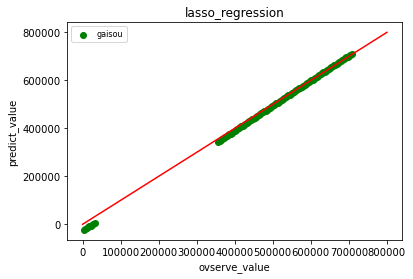
線形回帰のLasso回帰は、外挿の予測がよくできています。
数値予測の時の外挿は、よほど気をつけないといけないですね。3つのうちの一つだけが、学習の特徴量から外れているだけで、線形回帰以外は、こんな結果になってしまうから、気をつけましょう。
少しでも外挿しようと思ったら、線形回帰で外挿を使いましょう。
今日はここまでですが、逆に内挿に見えて外挿というのはどうなのでしょうか?
問3:小さい値と大きい値で学習して、その間は予測できるか?
想像すれば、これも線形回帰以外は予測できないよね、きっと。
これは次の記事で
機械学習は平行四辺形を予測できるか?(2)内挿みたいなのに外挿ってどうなるかな??
では、この平行四辺形辺は続きます。