はじめに
唐突ですが先日、下記のQiita記事が公開され一大ニュースとなりました。(主に私の中で。)
簡単に実行できた! "強化学習 DQN vs ゲーム 2048"
「簡単に実行できた!」のタイトルに偽りはなく、わずか30分程度で強化学習が動かせるようになり非常に感動しました。ありがとうMATLAB、ありがとう@HYCE さん。これでまた、MATLABを使ったお遊び科学技術の学習が一つ捗ります。
こちらの記事を参考に30分ほど頑張った結果、MATLABの強化学習が簡単に出来た!(中身を理解できたとは言ってない)https://t.co/8FxHChca3W
— モータ制御マン (@motorcontrolman) November 23, 2020
MATLABの強化学習ツールボックスは現状英語ドキュメントしかないので日本語での解説記事は本当に助かります。 pic.twitter.com/NrF3FguEKq
…しかしながらなぜかその心には、虚しさが感じられるのであった。
なぜか。それは、学習対象のゲーム「2048」のコードがボリュームありすぎて、好きにいじくり回せないからに他なりません。
なぜ「対象を好きにいじくり回すこと」に重きを置くかと言うと、それは強化学習ツールの対象を通してその特性を把握したいからです。強化学習ツールの中身は極めて高度&ブラックボックッスであり、これ自体を理解・分析するのは骨が折れます。なのでその対象をあーだこーだすることで間接的に理解したいのです。
前置きが長くなりました。「単振子」の単語でこのページを開いた方、お待たせしました。
本記事では、強化学習の題材として最もシンプルな「単振子」をMATLABのクラスで実装する方法について記します。
なぜクラスで実装するかというと、クラス化することで強化学習ツールの学習対象とした場合の見通しが良いからです。(詳細はおまけ②に記載)
また強調しておくと、本記事をきっかけにMATLABにおける物理モデルの強化学習に挑もうという方は、他の部分は読み飛ばしてもよいので 最大のポイント:ハンドルクラスを使用するをお読み下さい。正直ここだけ抑えておけば強化学習の対象を自分で簡単に作れます。
本記事を通して自分で強化学習の対象モデルを準備、そして強化学習ツールボックスにどしどし突っ込んで頂ければ幸いです。強化学習ツールボックスを所持する人まだ少なそうだけど…
なおMATLABのバージョンとしては2020bを使用していますが、これはあくまでReinforcement Learning Toolboxを利用するためです。
単振子の実装やクラス化はそれ以前のバージョンでも概ね同じと思います。また強化学習をしないのであれば特別なToolboxは不要です。
MATLABの強化学習で倒立振子を立たせたりしている(立ったとは言っていない) pic.twitter.com/WbwT6x89Sm
— モータ制御マン (@motorcontrolman) December 13, 2020
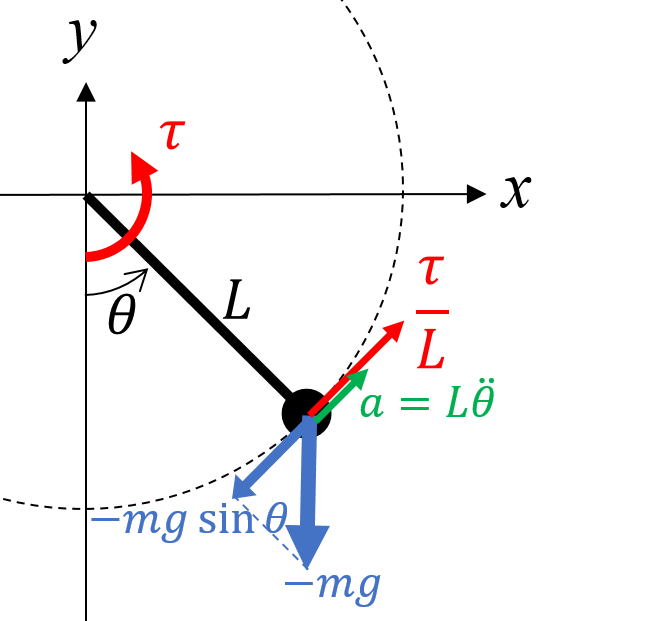
1. 運動方程式の導出
基本的には下記のページに書いてある通りですが、著者の学習目的でここに導出式を示します。
KIT物理ナビゲーション 単振り子:運動方程式
並進運動における運動方程式は一般に下記にて与えられます。
ma(t) = F(t)
上記においてmは質点の質量[kg]、a(t)は加速度[m/s^2]、F(t)は力[N]を意味します。
単振子においては、質点の接線方向の運動方程式を考えるものとします。このとき、速度v(t)[m/s]は下記にて表されます。
v(t) = L\omega(t)=L\dot{\theta}(t)
ここで、Lは棒の長さ[m]、ω(t)は角速度[rad/s]、θ(t)は角度[rad]を意味します。
加速度a(t)は速度v(t)の時間微分であるため下記のように表されます。
a(t) = \frac{d}{dt}v(t) =L\ddot{\theta}(t)
一方で、接線方向にかかる力F(t)は下記にて表される。
F(t) = -mg\sin\theta(t) +\frac{1}{L}\tau(t)
gは重力加速度[m/s^2]、τ(t)はトルク[Nm]を意味します。
並進方向の運動方程式にa(t)、F(t)を代入すると下記式を得ることができます。
mL\ddot{\theta}(t) = -mg\sin\theta(t) +\frac{1}{L}\tau(t) \\
上記式を整理することで、単振子の運動方程式が得られます。
\ddot{\theta}(t) = -\frac{g}{L}\sin\theta(t) +\frac{1}{mL^{2}}\tau(t)
2. 運動方程式を離散時間表現する
本来であれば、二輪台車シミュレーションをMATLABで実装する でやったようにラプラス変換→離散化の順を追って式を導出すべきですが、下記簡略化した方式を示します。(結構これでやっている人も多いのでは?)
連続時間系の式を離散時間系の式に置き換えることで下記が得られます。θの2階微分はそのままにしておきます。
\ddot{\theta}(n) = -\frac{g}{L}\sin\theta(n) +\frac{1}{mL^{2}}\tau(n)
θ(n)とその2階微分値は同時に得ることができないため、妥協案としてθ(n-1)を使います。
\ddot{\theta}(n) = -\frac{g}{L}\sin\theta(n-1) +\frac{1}{mL^{2}}\tau(n)
上記よりθの2階微分が求まるので、後退差分による積分を用いることでθの1階微分、およびθを下記求めます。
\dot{\theta}(n)=\dot{\theta}(n-1) + \ddot{\theta}(n)T_s \\
\theta(n)=\theta(n-1) + \dot{\theta}(n)T_s
ここでTsは離散時間を意味する。
やや乱暴ですが、上記によって離散化された単振子のモデル式が得られました。
3. 単振子のクラスを作成する
最大のポイント:ハンドルクラスを使用する
冒頭でも言及したように、本記事で最も伝えたい内容はこれです。
私自身、今までにもMATLABのクラスを作成したことはあったのですが「値クラス」と「ハンドルクラス」を明確に使い分けたことがなく、このため今回のクラス作成にて躓きました。
値クラス、ハンドルクラスについては、Mathworksの公式ドキュメントにて下記のように紹介されています。
https://jp.mathworks.com/help/matlab/matlab_oop/comparing-handle-and-value-classes.html
値クラスについて:
"value" クラス コンストラクターは、代入先の変数に関連付けられたオブジェクトを返します。この変数を代入し直すと、MATLAB® は元のオブジェクトの独立したコピーを作成します。
ハンドルクラスについて:
handle クラス コンストラクターは、作成されたオブジェクトへの参照であるハンドル オブジェクトを返します。MATLAB にオリジナル オブジェクトのコピーを作成させないで、ハンドル オブジェクトを複数の変数に割り当てたり、あるいはそれを関数に渡したりすることができます。
上記、直訳すぎて何を言っているかやや分かりにくい(少なくとも私にとって)ですが、要するに「値クラス」だと変数を代入する度にオブジェクトのコピーが作成されます。
これの何が問題かと言うと、前回値に対し今回値を加算すると言った処理が出来ないということです。すなわち、物理モデルはハンドルクラスとして定義しておかないと期待通りに動かないということです。
なおこれは物理モデルに限ったことではなく、今回値=前回値+αという措置が必要な対象において全般的に言えることなのでクラス作成の場合は注意しましょう。
ところで、MATLAB/Simulinkアドベントカレンダー2020にてこの「ハンドルクラスの使用」を強調した記事が他2本もあります。
MATLAB with オブジェクト指向 への乗り換えガイド
全天球イラスト作画補助ツール(VRビューア)をMATLABで作った話
あえて繰り返そう。
MATLABのクラスはとりあえずハンドルクラス使っときゃええねん。
アドベントカレンダー19日目、 @larking95 さんによる
— モータ制御マン (@motorcontrolman) December 19, 2020
MATLABにおけるオブジェクト指向の詳細解説!
クラスって多様性やSetter・Getter出来たんですね…。ここまで分かり易く書いて頂いたおかげで理解できました。とりあえずハンドルクラス使っときゃええねんは強く同意。https://t.co/b2Sarx5aUO
実際に作成した単振子のクラス
1行目に< handleと書くことでハンドルクラスとして定義されます。
classdef classPendulum < handle
properties
L = 1;
m = 0.5;
Theta = 0;
AngVelocity = 0;
AngAccel = 0;
Ts = 0.05;
X;
Y;
Energy = 0;
end
properties (Access = private)
hVec;
hText;
g = 9.8;
end
methods
% クラスの初期化処理
function obj = classPendulum(L, m, Theta, AngVelocity, Ts)
obj.L = L;
obj.m = m;
obj.Theta = Theta;
obj.AngVelocity = AngVelocity;
obj.Ts = Ts;
% figureの作成
obj.X = obj.L * sin(obj.Theta);
obj.Y = -obj.L * cos(obj.Theta);
obj.hVec = quiver(0, 0, obj.X, obj.Y,'k','LineWidth', 0.5 ,'MaxHeadSize',0.4);
obj.hText = text(0.5,-1, '0','FontSize',14);
axis([-1.5 1.5 -1.5 1.5]);
end
% 離散時間表現したモデル式の更新
function pstep(obj, tau)
obj.AngAccel = - obj.g/obj.L * sin(obj.Theta) + 1/(obj.m * obj.L^2) * tau;
obj.AngVelocity = obj.AngVelocity + obj.AngAccel * obj.Ts;
obj.Theta = obj.Theta + obj.AngVelocity * obj.Ts;
% 位置エネルギー + 運動エネルギーの計算
obj.Energy = obj.m * obj.g * (obj.Y + obj.L) + 1/2 * obj.m * ( obj.L * obj.AngVelocity ) ^2;
% Figureの更新
obj.X = obj.L * sin(obj.Theta);
obj.Y = -obj.L * cos(obj.Theta);
obj.hVec.UData = obj.X;
obj.hVec.VData = obj.Y;
obj.hText.String = "tau: " + num2str(tau) + newline + ...
"Y: " + num2str(obj.Y) + newline + ...
"Energy: " + num2str(obj.Energy);
drawnow
end
end
end
上記の単振子クラスを、下記簡単なコードにて動作検証します。内容としては、θ=30deg条件からトルク0Nmで動作させたものとなります。詳細については割愛。
clear all;
close all;
% 単振子のパラメータ
L = 1;
m = 2;
Ts = 0.02;
% 時間設定
Tfin = 5;
t1 = [0:Ts:Tfin];
% 単振子クラスの作成
pendulum = classPendulum(L, m, pi/6, 0, Ts);
%% 振り子の動作
for i = 1:length(t1)
Trq = 0;
pendulum.pstep(Trq);
end
関数 pendulum.pstep(Trq) にて、Trqを入力トルクとした振子モデルの離散時間が1つ進みます。ポイントとして、クラス定義時はfunction pstep(obj, tau)のように書きますが、オブジェクト自らを引数とする場合はobjを省略可能です。
テストの結果については下記。
単振子クラスの動作テスト①ハンドルクラスの場合 pic.twitter.com/dkX0ceVOlg
— モータ制御マン (@motorcontrolman) December 13, 2020
ハンドルクラスにしなかった場合、すなわち< handleを書かなかった場合は下記。
単振子クラスの動作テスト②値クラスの場合(動きません) pic.twitter.com/a0jLhbbXEp
— モータ制御マン (@motorcontrolman) December 13, 2020
おあとがよろしいようで。
おまけ① 強化学習(DQN)のための最小限のコード
簡単に実行できた! "強化学習 DQN vs ゲーム 2048" を大いに参考に作成。なくても動作上問題ない設定とかは省略しています。
報酬の定義はステップ関数内に書いていますので、遊ばれる方はこちらをいじってみて下さい。
強化学習の実行コード
clear all;
close all;
L = 1;
m = 2;
Ts = 0.02;
pendulum = classPendulum(L, m, pi/6, 0, Ts);
%% 状態のサイズと上下限を定義
ObservationInfo = rlNumericSpec([2 1],'LowerLimit',[-pi; -10],'UpperLimit',[pi; 10]);
%% 行動の定義
% トルク= -3Nm、0Nm、3Nmを行動として定義
ActionInfo = rlFiniteSetSpec([-3 0 3]);
%% ステップ関数、リセット関数の定義
ResetHandle = @()myResetFunction(pendulum);
StepHandle = @(Action,LoggedSignals) myStepFunction(Action,LoggedSignals,pendulum);
% 環境、エージェントの定義
env = rlFunctionEnv(ObservationInfo, ActionInfo, StepHandle,ResetHandle);
agent = rlDQNAgent(ObservationInfo,ActionInfo);
%% エージェントの詳細設定
agent.AgentOptions.EpsilonGreedyExploration.Epsilon = 0.95;
agent.AgentOptions.EpsilonGreedyExploration.EpsilonDecay = 0.0001;
agent.AgentOptions.EpsilonGreedyExploration.EpsilonMin = 0.1;
%% 学習のオプション設定
opt = rlTrainingOptions("MaxEpisodes",15000,...
"MaxStepsPerEpisode",550,...
"StopTrainingCriteria","AverageReward",...
"StopTrainingValue",50000,...
"UseParallel", false,...
"ScoreAveragingWindowLength",50);
%% 学習の実施
trainStats = train(agent,env,opt);
リセット関数
LoggedSignal.State = state;
InitialObservation = LoggedSignal.State;
end
</div></details>
<details><summary>ステップ関数</summary><div>
```matlab:myStepFunction.m
function [NextObs,Reward,IsDone,LoggedSignals] = myStepFunction(Action, LoggedSignals,pendulum)
% State before move 操作する前の状態を取得
statePre = [0;0];
statePre(1) = pendulum.Theta;
statePre(2) = pendulum.AngVelocity;
Energy_pre = pendulum.Energy;
% Move
pendulum.pstep(Action);
% State update 操作後の状態を取得
state = [0;0];
state(1) = pendulum.Theta;
state(2) = pendulum.AngVelocity;
Energy = pendulum.Energy;
LoggedSignals.State = state;
% Next Observation
NextObs = LoggedSignals.State;
% Check terminal condition
IsDone = false; %強化学習修了条件なし
%% 報酬の計算
% エネルギーの増減
dEnergy = Energy - Energy_pre;
% Yがある程度まで降り上がっていれば高報酬
if pendulum.Y > pendulum.L * 0.8
Reward = 100;
else % それ以外は、ネルギーの増減から報酬を決定
if dEnergy > 0.005
Reward = 300 * dEnergy;
elseif dEnergy < 0
Reward = 500 * dEnergy;
else
Reward = 0;
end
end
end
おまけ②Mathworks公式の倒立振子×強化学習のサンプル
下記2つが準備されています。
a. 台車倒立振子×強化学習
よく見てみると、倒立振子をクラス化せずにステップ関数内で更新かけてますね。
前回の状態に対し、微分した状態にTsをかけて加算しているので後退差分による離散化の匂いがしますね。
% Apply motion equations.
ThetaDotDot = (Gravity*SinTheta - CosTheta*temp) / ...
(HalfPoleLength*(4.0/3.0 - PoleMass*CosTheta*CosTheta/SystemMass));
XDotDot = temp - PoleMass*HalfPoleLength*ThetaDotDot*CosTheta/SystemMass;
% Perform Euler integration.
LoggedSignals.State = State + Ts.*[XDot;XDotDot;ThetaDot;ThetaDotDot];
b. 単振子×強化学習 画像による状態監視ver
題材としては本記事と同じく単振子ですが、状態監視に角速度だけでなく画像を使っているようです。深層学習コテコテすぎて「ひゃ~」という感じがしますね。
おわりに
世の中、オープンソースだなんだと騒がれており0からプログラミングをする機会は減っていると思います。
が、私個人の趣味趣向としては、その中身を全く理解せずに使うのはなんだか気持ち悪くてできません。せめて、「多分こうなってるんだろうなぁ」というところまでは辿り着き、納得した上でやっとこれらを使う気持ちになれます。
「多分こうなってるんだなぁ」となるために必要なことは、やはり0から構築してきた経験の積み重ねだと思います。単振子モデルに限らず、簡単なもので良いので制御対象モデルおよび制御器を自分で書いてみることをオススメします。