この記事は Akerun Advent Calendar 2019 の11日目です。
目的
前回の記事ではPostgreSQLでt分布の累積分布関数を実装し、t検定を行いました。
そうなると逆の操作もやってみたくなるのが人情です。
t分布に基づく信頼区間の推定もSQLで実装できないでしょうか。
信頼区間を計算するには、t分布の累積分布関数の逆関数が必要です。
%点を返す関数なので、パーセンタイル関数とも呼ばれます。
たとえばEXCELなら T.INV 関数で呼び出すことができます。
しかしSQLにはそういった便利な関数がありません。
nが十分大きい場合は(よく言われるのは30以上なら)t分布を正規分布で近似できますが、SQLには正規分布の累積分布関数の逆関数も用意されていません。
仕方がないのでt分布の累積分布関数の逆関数をSQLで自作することにします。
SQLはPostgreSQLを使います。
SQLにこだわるのは、MetabaseのようなBIツール上で動作させたいからです。
有意水準αや、標本となる値の絞り込み条件をGUI上で操作しながら統計処理を実行できれば、無償のソフトウェア(Metabase, PostgreSQL)だけで高度なGUI・統計処理・柔軟なDBの3つを同時に実現できます。
実装方針
近似式を使う方法
インターネット上を探し回った結果、C言語による実装例やJavaScriptによる実装例を見つけました。
しかしいずれも、コードの根拠となる近似式の数式や説明を見つけられませんでした。インターネットではなく数学書や論文をあたらないとダメなんでしょうか。
これらの実装をSQLに移植して動作させることはできるかもしれませんが、なぜその実装で良いのかを自分で説明できないので、記事にするには向かない気がしました。
なにより、どちらも魔法の数字が複雑に乱れ飛ぶコードであり、実行速度や計算精度は良いだろうと思いますが、自分で書いていて楽しくなさそうなので、近似式を用いる方法はボツにしました。
ニュートン法を使う方法
というわけで、前回もお世話になったPascalによるt分布の実装のページを参考に、ニュートン法を用いて逆関数を実装することにしました。
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
累積分布関数と、累積分布関数の微分である確率密度関数があれば、ニュートン法で解を求めることができます。
前回作成した関数が活用できるのが気持ちいいですね。
実装
以下のコードはPostgreSQL v12.1 とMetabase v0.33.6 で動作確認しています。
{{}} はMetabaseのSQLパラメータ表記です。
Metabseを使わない場合は、実際の値か変数に置き換えてください。
Metabaseの制約上、SQLはワンクエリでなくてはいけないので、CTE(WITH句)を多用します。
t分布の確率密度関数
自由度vのt分布の確率密度関数はベータ関数を用いて表すことができます。
P(x) = \frac{1}{\sqrt{v}B(\frac{1}{2},\frac{v}{2})}\Bigl(1+\frac{x^2}{v}\Bigr)^{-(\frac{v+1}{2})}
前回の記事で作成したベータ関数を少し改造すれば、t分布の確率密度関数が完成します。
パラメータはv, xの2つです。
WITH
t_b1 AS (
WITH RECURSIVE t(n, pn) AS (
VALUES (0.0, 1.0::float)
UNION ALL
SELECT
n + 1.0 AS "n",
pn * ((0.5+n) * (1.0-({{v}}/2.0)+n)) / ((1.5+n) * (1.0+n)) AS "pn"
FROM t
WHERE n < 1000 AND ABS(pn) > 1e-20
),
t2 AS (
SELECT sum(pn) AS "2F1(a,1-b,a+1;1)"
FROM t
)
SELECT "2F1(a,1-b,a+1;1)" / 0.5 AS "B(1/2,v/2)" FROM t2
)
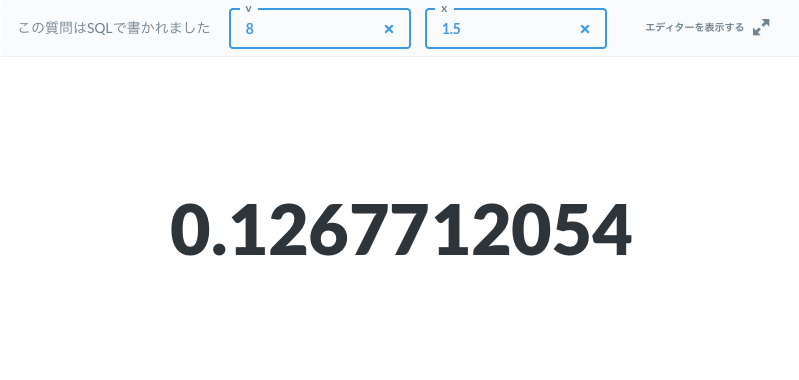
SELECT (1 + (({{x}}^2) / {{v}})) ^ ((-{{v}}-1.0)/2.0) / ("B(1/2,v/2)" * SQRT({{v}})) AS "P(x)"
FROM t_b1
実行結果
t分布の累積分布関数の逆関数
確率密度関数$pdf(x)$を、前回作成したt分布の累積分布関数$cdf(x)$と合体させてニュートン法を実行します。
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - \frac{cdf(x_n)}{pdf(x_n)}
収束は比較的早いようで、以下の例ではニュートン法のループを10回で打ち切っています。
パラメータは自由度vと確率pの2つです。
WITH RECURSIVE tinv(m, px) AS (
VALUES (0.0, 1.0::float)
UNION ALL
SELECT
m + 1.0 AS "m",
px - (
(
-- 累積密度関数 CDF
WITH
t_params AS (
SELECT
(px + SQRT(px^2.0 + {{v}})) / (2.0 * SQRT(px^2.0 + {{v}})) AS "z",
{{v}} / 2.0 AS "v/2"
),
t_bz AS (
WITH RECURSIVE t(n, pn) AS (
VALUES (0.0, 1.0::float)
UNION ALL
SELECT
n + 1.0 AS "n",
pn * z * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
FROM t, t_params
WHERE n < 1000 AND ABS(pn) > 1e-20
),
t2 AS (
SELECT sum(pn) AS "2F1(a,1-b,a+1;z)"
FROM t
)
SELECT "2F1(a,1-b,a+1;z)" * (z)^("v/2") / ("v/2") AS "Bz(v/2,v/2)" FROM t2, t_params
),
t_b1 AS (
WITH RECURSIVE t(n, pn) AS (
VALUES (0.0, 1.0)
UNION ALL
SELECT
n + 1.0 AS "n",
pn * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
FROM t, t_params
WHERE n < 1000 AND ABS(pn) > 1e-20
),
t2 AS (
SELECT sum(pn) AS "2F1(a,1-b,a+1;1)"
FROM t
)
SELECT "2F1(a,1-b,a+1;1)" / "v/2" AS "B(v/2,v/2)" FROM t2, t_params
)
SELECT ("Bz(v/2,v/2)" / "B(v/2,v/2)") - {{p}} AS "pd" FROM t_bz, t_b1
)
/
(
-- 確率密度関数 PDF
WITH
t_b1 AS (
WITH RECURSIVE t(n, pn) AS (
VALUES (0.0, 1.0::float)
UNION ALL
SELECT
n + 1.0 AS "n",
pn * ((0.5+n) * (1.0-({{v}}/2.0)+n)) / ((1.5+n) * (1.0+n)) AS "pn"
FROM t
WHERE n < 1000 AND ABS(pn) > 1e-20
),
t2 AS (
SELECT sum(pn) AS "2F1(a,1-b,a+1;1)"
FROM t
)
SELECT "2F1(a,1-b,a+1;1)" / 0.5 AS "B(1/2,v/2)" FROM t2
)
SELECT (1 + ((px^2) / {{v}})) ^ ((-{{v}}-1.0)/2.0) / ("B(1/2,v/2)" * SQRT({{v}})) FROM t_b1))
FROM tinv
WHERE m < 10
)
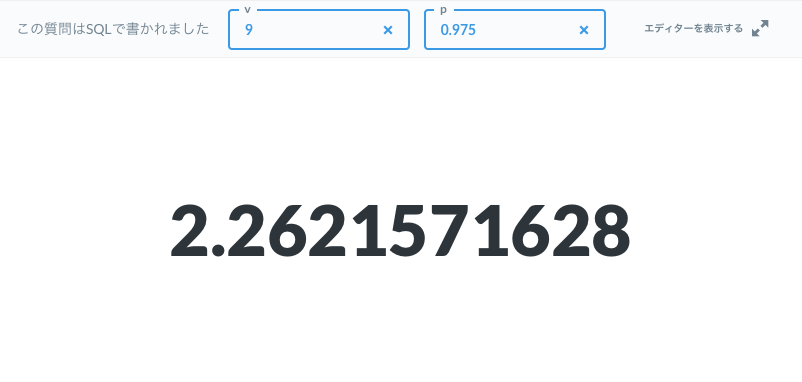
SELECT px FROM tinv ORDER BY m DESC LIMIT 1
WITH RECURSIVE が入れ子になる、かなり見苦しいコードになっていますが、どうにか実装できました。
実行結果
信頼区間を計算する
t分布の累積分布関数の逆関数が実装できたので、実際に使ってみましょう。
テーブル t_samples のカラム num に、母平均の信頼区間を推定したい値が保存されているとします。
以下の例では VALUES でサンプルデータを作成していますが、実際に使用する際はこの箇所でDBから実データを取得してください。
自由度vは入力データから計算されるので、パラメータは有意水準α(alpha)のみです。
WITH
t_samples AS (
SELECT *
FROM (
VALUES (2.33), (2.13), (0.45), (1.34), (4.27), (2.10), (3.12), (-2.09), (2.49), (-0.32)
) AS t(num)
),
t_input AS (
SELECT
AVG(num) AS "avg",
STDDEV(num) AS "s",
STDDEV(num) / SQRT(COUNT(num)) AS "se",
COUNT(num) - 1 AS "v"
FROM t_samples
),
t_ppf AS (
WITH RECURSIVE tinv(m, px) AS (
VALUES (0.0, 1.0::float)
UNION ALL
SELECT
m + 1.0 AS "m",
px - (
(
-- 累積密度関数 CDF
WITH
t_params AS (
SELECT
(px + SQRT(px^2.0 + v)) / (2.0 * SQRT(px^2.0 + v)) AS "z",
v / 2.0 AS "v/2"
FROM t_input
),
t_bz AS (
WITH RECURSIVE t(n, pn) AS (
VALUES (0.0, 1.0::float)
UNION ALL
SELECT
n + 1.0 AS "n",
pn * z * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
FROM t, t_params
WHERE n < 1000 AND ABS(pn) > 1e-20
),
t2 AS (
SELECT sum(pn) AS "2F1(a,1-b,a+1;z)"
FROM t
)
SELECT "2F1(a,1-b,a+1;z)" * (z)^("v/2") / ("v/2") AS "Bz(v/2,v/2)" FROM t2, t_params
),
t_b1 AS (
WITH RECURSIVE t(n, pn) AS (
VALUES (0.0, 1.0)
UNION ALL
SELECT
n + 1.0 AS "n",
pn * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
FROM t, t_params
WHERE n < 1000 AND ABS(pn) > 1e-20
),
t2 AS (
SELECT sum(pn) AS "2F1(a,1-b,a+1;1)"
FROM t
)
SELECT "2F1(a,1-b,a+1;1)" / "v/2" AS "B(v/2,v/2)" FROM t2, t_params
)
SELECT ("Bz(v/2,v/2)" / "B(v/2,v/2)") - (1-{{alpha}}/2.0) AS "pd" FROM t_bz, t_b1
)
/
(
-- 確率密度関数 PDF
WITH
t_b1 AS (
WITH RECURSIVE t(n, pn) AS (
VALUES (0.0, 1.0::float)
UNION ALL
SELECT
n + 1.0 AS "n",
pn * ((0.5+n) * (1.0-(v/2.0)+n)) / ((1.5+n) * (1.0+n)) AS "pn"
FROM t, t_input
WHERE n < 1000 AND ABS(pn) > 1e-20
),
t2 AS (
SELECT sum(pn) AS "2F1(a,1-b,a+1;1)"
FROM t
)
SELECT "2F1(a,1-b,a+1;1)" / 0.5 AS "B(1/2,v/2)" FROM t2
)
SELECT (1 + ((px^2) / v)) ^ ((-v-1.0)/2.0) / ("B(1/2,v/2)" * SQRT(v)) FROM t_b1, t_input))
FROM tinv
WHERE m < 10
)
SELECT px AS "ppt" FROM tinv ORDER BY m DESC LIMIT 1
)
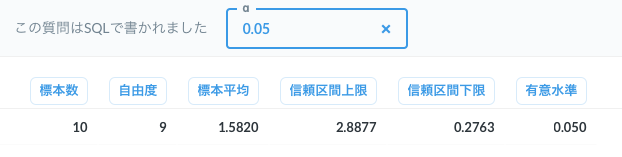
SELECT
v + 1 AS "標本数",
v AS "自由度",
avg AS "標本平均",
avg + (ppt * se) AS "信頼区間上限",
avg - (ppt * se) AS "信頼区間下限",
{{alpha}} AS "有意水準"
FROM t_input, t_ppf
感想
精度
自由度vがかなり小さい時、特にv=1の場合の精度が悪いです。
これはベータ関数の収束が悪いためで、nを増やしてもなかなか精度が上がりませんでした。
実用上は、そこまで小さなデータセットに対して信頼区間を求めたいことは少ないとは思いますが。
複雑さ
クエリがかなり長く、分かりにくくなってしまいました。
実用上は、ストアド関数にしたほうが良いかも知れません。
実用性
あると思います。
前回と今回の記事を書いていて思いましたが、SQL標準でt分布の関数が用意されていれば、使う場面は多そうです。
ExcelやOracleには搭載されているものなので、PostgreSQLにも標準で実装されると嬉しいです。そうなれば、こんな大変なSQLを書く必要はなくなります。