PostgreSQLでt検定を実装する

この記事は Akerun Advent Calendar 2019 の4日目です。

目的

以前の記事ではMetabaseを使ってカプラン・マイヤー推定量を計算し描画しました。

MetabaseとSQLの力を使えば、他にもさまざまな統計処理ができそうな気がします。

例えば、有名な統計的検定のひとつにt検定があります。
現在ではRやPython, Excelなど、統計専門のソフトウェアでなくてもt検定は簡単に実施することができます。

t検定を行うにはt分布の累積確率を計算する必要があります。
たとえばExcelであれば T.DIST 関数でt分布の累積分布関数を呼び出し、t分布の累積確率を計算できます。

しかしSQLにはそういった便利な関数がありません。
nが十分大きい場合は（よく言われるのは30以上なら）t分布を正規分布で近似できますが、SQLには正規分布の累積分布関数も用意されていません。

仕方がないので、t分布の累積分布関数をSQLで自作することにします。
SQLはPostgreSQLを使います。

SQLにこだわるのは、MetabaseのようなBIツール上で動作させたいからです。

有意水準αや、標本となる値の絞り込み条件をGUI上で操作しながら統計処理を実行できれば、無償のソフトウェア(Metabase, PostgreSQL)だけで高度なGUI・統計処理・柔軟なDBの３つを同時に実現できます。

実装方針

自由度$v$のt分布の累積分布関数は以下の数式で表されます。

\int_{-\infty}^{t}f(u)du = I_z(\frac{v}{2} ,\frac{v}{2})

ただし、

z = \frac{t+\sqrt{t^2+v}}{2\sqrt{t^2+v}}

$I_z(a,b)$ は正則ベータ関数（正則不完全ベータ関数）と呼ばれる関数で、

I_z(a,b) = \frac{B_z(a,b)}{B(a,b)}

です。

ここで $B_z(a,b)$ は不完全ベータ関数、$B(a,b)$ は（通常の）ベータ関数と呼ばれる関数です。ベータ関数 $B(a,b)$ は不完全ベータ関数 $Bz(a,b)$ の $z=1$ の場合なので、不完全ベータ関数 $B_z(a,b)$ を実装できればベータ関数も同時に実装できそうです。

不完全ベータ関数は以下の積分で定義されます。

B_z(a,b) = \int_{0}^{z}t^{a-1}(1-t)^{b-1}dt

しかしこの積分はそのままでは計算できないので、超幾何級数（ガウスの超幾何関数）による式を使います。

B_z(a,b) = \frac{z^a}{a}{_2F_1(a,1-b,a+1;z)}\\

ここで、

_2F_1(a,b,c;z) = \sum_{n=0}^{\infty} P_n(a,b,c;z)\\
P_0(a,b,c;z) = 1\\
P_{n+1}(a,b,c;z) = \frac{(a+n)(b+n)}{(c+n)(1+n)}zP_n(a,b,c;z)

です。
これなら、再帰を使えば計算できそうです。
さいわい、PostgreSQLは再帰計算ができます。
それではSQLを書いてみましょう。

実装

以下のコードはPostgreSQL v12.1 とMetabase v0.33.6 で動作確認しています。

{{}} はMetabaseのSQLパラメータ表記です。
Metabseを使わない場合は、実際の値か変数に置き換えてください。
Metabaseの制約上、SQLはワンクエリでなくてはいけないので、CTE(WITH句)を多用します。

Step 1: ガウスの超幾何関数

_2F_1(a,b,c;z) = \sum_{n=0}^{\infty} P_n(a,b,c;z)\\
P_0(a,b,c;z) = 1\\
P_{n+1}(a,b,c;z) = \frac{(a+n)(b+n)}{(c+n)(1+n)}zP_n(a,b,c;z)

n = 0, pn = 1 を初期値とし、 nを∞に向けて大きくしながら$P_n$を再帰計算します。実際には無限には計算できないので、途中で打ち切ります。最後に$P_n$を SUM します。

以下の例では n = 1000 、または、アンダフローを回避するために項の値が1e-20以下になった時点で打ち切っています。

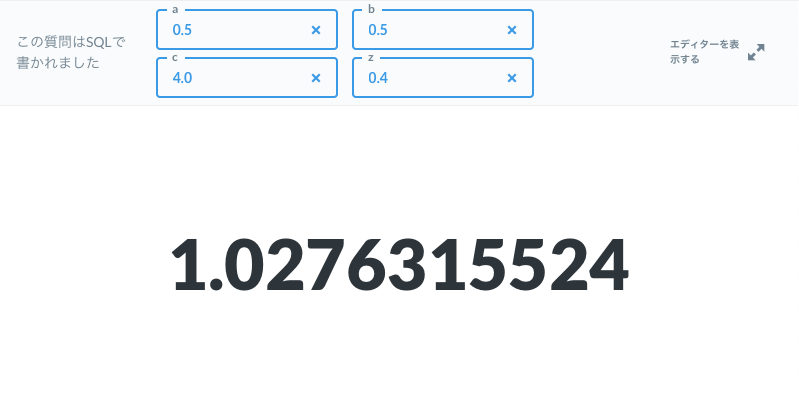
パラメータはa, b, c, zの4つです。

WITH RECURSIVE t(n, pn) AS (
    VALUES (0.0, 1.0::float)
    UNION ALL
    SELECT
        n + 1.0 AS "n",
        pn * {{z}} * (({{a}}+n) * ({{b}}+n)) / (({{c}}+n) * (1.0+n)) AS "pn"
    FROM t
    WHERE n < 1000 AND ABS(pn) > 1e-20
)
SELECT sum(pn) AS "2F1(a,b,c;z)" FROM t

実行結果

Step 2: 不完全ベータ関数とベータ関数

B_z(a,b) = \frac{z^a}{a}{_2F_1(a,1-b,a+1;z)}\\

超幾何関数に少し手を加えるだけで完成です。
パラメータはa, b, zの3つです。

WITH RECURSIVE t(n, pn) AS (
    VALUES (0.0, 1.0::float)
    UNION ALL
    SELECT
        n + 1.0 AS "n",
        pn * {{z}} * (({{a}}+n) * (1.0-{{b}}+n)) / (({{a}}+1.0+n) * (1.0+n)) AS "pn"
    FROM t
    WHERE n < 1000 AND ABS(pn) > 1e-20
)
SELECT sum(pn) * {{z}}^{{a}} / {{a}} AS "Bz(a,b)" FROM t

通常のベータ関数はこれの $z=1$ の場合なので、より簡単に書くことができます。
パラメータはa, bの2つです。

WITH RECURSIVE t(n, pn) AS (
    VALUES (0.0, 1.0::float)
    UNION ALL
    SELECT
        n + 1.0 AS "n",
        pn * (({{a}}+n) * (1.0-{{b}}+n)) / (({{a}}+1.0+n) * (1.0+n)) AS "pn"
    FROM t
    WHERE n < 1000 AND ABS(pn) > 1e-20
)
SELECT sum(pn) / {{a}} AS "B(a,b)" FROM t

Step 3: 正則ベータ関数

I_z(a,b) = \frac{B_z(a,b)}{B(a,b)}

2種類のベータ関数を割り算するだけです。
Step 2で作ったSQLを合体させましょう。
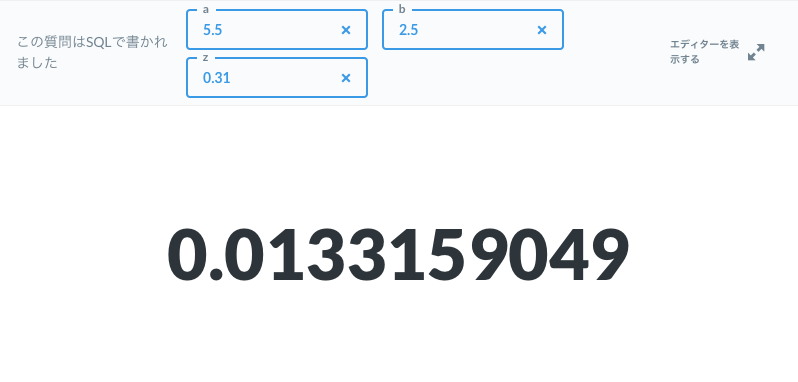
パラメータはa, b, zの3つです。

WITH
t_bz AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0::float)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * {{z}} * (({{a}}+n) * (1.0-{{b}}+n)) / (({{a}}+1.0+n) * (1.0+n)) AS "pn"
        FROM t
        WHERE n < 1000 AND ABS(pn) > 1e-20
    )
    SELECT sum(pn) * {{z}}^{{a}} / {{a}} AS "Bz(a,b)" FROM t
),
t_b1 AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * (({{a}}+n) * (1.0-{{b}}+n)) / (({{a}}+1.0+n) * (1.0+n)) AS "pn"
        FROM t
        WHERE n < 1000 AND ABS(pn) > 1e-20
    )
    SELECT sum(pn) / {{a}} AS "B(a,b)" FROM t
)
SELECT "Bz(a,b)" / "B(a,b)" AS "Iz(a,b)" FROM t_bz, t_b1

実行結果

Step 4: t分布の累積分布関数

\int_{-\infty}^{t}f(u)du = I_z(\frac{v}{2} ,\frac{v}{2})\\
z = \frac{t+\sqrt{t^2+v}}{2\sqrt{t^2+v}}

a, bが自由度$v$に置き換わり、$z$は$v$と$t$から計算した値に置き換わります。よってパラメータはv, tの2つです。

WITH
t_params AS (
    SELECT
        ({{t}} + SQRT({{t}}^2.0 + {{v}})) / (2.0 * SQRT({{t}}^2.0 + {{v}})) AS "z",
        {{v}} / 2.0 AS "v/2"
),
t_bz AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0::float)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * z * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
        FROM t, t_params
        WHERE n < 1000 AND ABS(pn) > 1e-20
    ),
    t2 AS (
        SELECT sum(pn) AS "2F1(a,1-b,a+1;z)"
        FROM t
    )
    SELECT "2F1(a,1-b,a+1;z)" * (z)^("v/2") / ("v/2") AS "Bz(v/2,v/2)" FROM t2, t_params
),
t_b1 AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
        FROM t, t_params
        WHERE n < 1000 AND ABS(pn) > 1e-20
    ),
    t2 AS (
        SELECT sum(pn) AS "2F1(a,1-b,a+1;1)"
        FROM t
    )
    SELECT "2F1(a,1-b,a+1;1)" / "v/2" AS "B(v/2,v/2)" FROM t2, t_params
)
SELECT "Bz(v/2,v/2)" / "B(v/2,v/2)" AS "Iz(v/2,v/2)" FROM t_bz, t_b1

t検定を行う

ついに累積分布関数が完成しました！
とても計算できそうに見えなかった積分も、最終的に加減乗除と平方根、冪乗だけで計算できることがわかりました。

それでは実際にt検定をやってみましょう。

1群のt検定

t検定の最も単純なパターンです。

テーブル t_samples のカラム num に、検定したい値が保存されているとします。numの平均値が0と有意に異なるかを検定します。

以下の例では VALUES でサンプルデータを作成していますが、実際に使用する際はこの箇所でDBから実データを取得してください。

簡単のためt値の絶対値をとって計算していますが、 SIGN で正負を保持し、最後の出力ではt値を本来の符号に復元しています。

PostgreSQLの stddev 関数は標本分散ではなく不偏分散の平方根を返すことに注意です。

WITH
t_samples AS (
    SELECT *
    FROM (
        VALUES (-6.3), (-2.1), (0.4), (1.4), (-4.8), (2.1), (-5.1), (-2.0)
    ) AS t(num)
),
t_input AS (
    SELECT
        ABS(AVG(num)) / (stddev(num) / sqrt(COUNT(num))) AS "t_abs",
        SIGN(AVG(num)) AS "t_sign",
        COUNT(num) - 1 AS "v"
    FROM t_samples
),
t_params AS (
    SELECT 
        ("t_abs" + SQRT("t_abs"^2.0 + v)) / (2.0 * SQRT("t_abs"^2.0 + v)) AS "z",
        v / 2.0 AS "v/2"
    FROM t_input
),
t_bz AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0::float)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            CASE 
            WHEN true THEN pn * z * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) 
            ELSE 0 
            END AS "pn"
        FROM t, t_params
        WHERE "n" < 1000 AND ABS(pn) > 1e-20
    ),
    t2 AS (
        SELECT sum(pn) AS "2F1(a,1-b,a+1;z)" 
        FROM t
    )
    SELECT "2F1(a,1-b,a+1;z)" * (z)^("v/2") / ("v/2") AS "Bz(v/2,v/2)" FROM t2, t_params
),
t_b1 AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
        FROM t, t_params
        WHERE n < 1000 AND ABS(pn) > 1e-20
    ),
    t2 AS (
        SELECT sum(pn) AS "2F1(a,1-b,a+1;1)" 
        FROM t
    )
    SELECT "2F1(a,1-b,a+1;1)" / "v/2" AS "B(v/2,v/2)" FROM t2, t_params
)
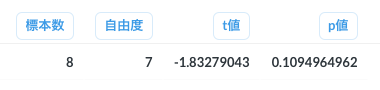
SELECT 
    v + 1 AS "標本数",
    v AS "自由度",
    "t_sign" * "t_abs" AS "t値",
    (1.0 - ("Bz(v/2,v/2)" / "B(v/2,v/2)")) * 2.0 AS "p値"
FROM t_bz, t_b1, t_input

実行結果

対応のある2群のt検定も、numを2群の差に置き換えることで同様に実行できます。

対応のない2群のt検定

対応のない2群の検定（分散が等しい場合）です。

sample_group	num
1	1.5
1	-2.5
2	4.0
2	0.5
...	...

上記のようなテーブルに検定したいデータがあるとします。sample_group 1と2のnumの平均値が有意に異なるかを検定します。

FILTER句を使って1行に展開するときれいに処理できます。
PostgreSQLの variance は標本分散ではなく、不偏分散を返すことに注意です。

WITH
t_samples AS (
    SELECT *
    FROM (
        VALUES 
            (1, 6.3), (1, 8.1), (1, 9.4), (1, 10.4), 
            (2, 4.8), (2, 2.1), (2, 5.1), (2, 2.0)
    ) AS t(sample_group, num)
),
t_samples_summary AS (
    SELECT
        COUNT(num) FILTER (WHERE "sample_group" = 1) AS "n1",
        COUNT(num) FILTER (WHERE "sample_group" = 2) AS "n2",
        VARIANCE(num) FILTER (WHERE "sample_group" = 1) AS "var1",
        VARIANCE(num) FILTER (WHERE "sample_group" = 2) AS "var2",
        AVG(num) FILTER (WHERE "sample_group" = 1) AS "avg1",
        AVG(num) FILTER (WHERE "sample_group" = 2) AS "avg2"
    FROM t_samples
),
t_input AS (
    SELECT
        ABS("avg1" - "avg2") / SQRT((((("n1"-1.0)*"var1")+(("n2"-1.0)*"var2")) / ("n1"+"n2"-2.0)) * ((1.0/"n1") + (1.0/"n2"))) AS "t_abs",
        SIGN("avg1" - "avg2") AS "t_sign",
        "n1" + "n2" - 2.0 AS "v"
    FROM t_samples_summary
),
t_params AS (
    SELECT 
        ("t_abs" + SQRT("t_abs"^2.0 + v)) / (2.0 * SQRT("t_abs"^2.0 + v)) AS "z",
        v / 2.0 AS "v/2"
    FROM t_input
),
t_bz AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0::float)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * z * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
        FROM t, t_params
        WHERE n < 1000
    ),
    t2 AS (
        SELECT sum(pn) AS "2F1(a,1-b,a+1;z)" 
        FROM t
    )
    SELECT "2F1(a,1-b,a+1;z)" * (z)^("v/2") / ("v/2") AS "Bz(v/2,v/2)" FROM t2, t_params
),
t_b1 AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
        FROM t, t_params
        WHERE n < 1000
    ),
    t2 AS (
        SELECT sum(pn) AS "2F1(a,1-b,a+1;1)" 
        FROM t
    )
    SELECT "2F1(a,1-b,a+1;1)" / "v/2" AS "B(v/2,v/2)" FROM t2, t_params
)
SELECT 
    "n1" AS "標本数1",
    "avg1" AS "平均1",
    "n2" AS "標本数2",
    "avg2" AS "平均2",
    "v" AS "自由度",
    "t_sign" * "t_abs" AS "t値",
    (1.0 - ("Bz(v/2,v/2)" / "B(v/2,v/2)")) * 2.0 AS "p値"
FROM t_bz, t_b1, t_input, t_samples_summary

実行結果

Welchのt検定

対応のない2群の検定（分散が等しくない場合）です。
検定に使うデータは分散が等しい場合と同じです。

自由度が非整数になるため数表での計算は困難ですが、今回作成した関数は最初から浮動小数点数に対応しているため何も問題はありません。等分散の検定から、t値と自由度の計算式を変更するだけでOKです。

WITH
t_samples AS (
    SELECT *
    FROM (
        VALUES (1, 2.0), (1, 0.0), (1, 3.0), (1, -3.0), (1, 4.0), (1, 1.0), (1, -1.0), (1, 4.0), (2, 5.0), (2, -1.0), (2, 2.0), (2, -1.0), (2, 7.0), (2, 3.0), (2, 4.0), (2, 5.0) 
    ) AS t(sample_group, num)
),
t_samples_summary AS (
    SELECT
        COUNT(num) FILTER (WHERE "sample_group" = 1) AS "n1",
        COUNT(num) FILTER (WHERE "sample_group" = 2) AS "n2",
        VARIANCE(num) FILTER (WHERE "sample_group" = 1) AS "var1",
        VARIANCE(num) FILTER (WHERE "sample_group" = 2) AS "var2",
        AVG(num) FILTER (WHERE "sample_group" = 1) AS "avg1",
        AVG(num) FILTER (WHERE "sample_group" = 2) AS "avg2"
    FROM t_samples
),
t_input AS (
    SELECT
        ABS("avg1" - "avg2") / SQRT(("var1"/"n1") + ("var2"/"n2")) AS "t_abs",
        SIGN("avg1" - "avg2") AS "t_sign",
        (("var1"/"n1") + ("var2"/"n2"))^2.0 / ((("var1"^2.0)/(("n1"^2.0)*("n1"-1.0))) + (("var2"^2.0)/(("n2"^2.0)*("n2"-1.0)))) AS "v"
    FROM t_samples_summary
),
t_params AS (
    SELECT 
        ("t_abs" + SQRT("t_abs"^2.0 + v)) / (2.0 * SQRT("t_abs"^2.0 + v)) AS "z",
        v / 2.0 AS "v/2"
    FROM t_input
),
t_bz AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0::float)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * z * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
        FROM t, t_params
        WHERE n < 1000 AND ABS(pn) > 1e-20
    ),
    t2 AS (
        SELECT sum(pn) AS "2F1(a,1-b,a+1;z)" 
        FROM t
    )
    SELECT "2F1(a,1-b,a+1;z)" * (z)^("v/2") / ("v/2") AS "Bz(v/2,v/2)" FROM t2, t_params
),
t_b1 AS (
    WITH RECURSIVE t(n, pn) AS (
        VALUES (0.0, 1.0)
        UNION ALL
        SELECT
            n + 1.0 AS "n",
            pn * (("v/2"+n) * (1.0-"v/2"+n)) / (("v/2"+1.0+n) * (1.0+n)) AS "pn"
        FROM t, t_params
        WHERE n < 1000 AND ABS(pn) > 1e-20
    ),
    t2 AS (
        SELECT sum(pn) AS "2F1(a,1-b,a+1;1)" 
        FROM t
    )
    SELECT "2F1(a,1-b,a+1;1)" / "v/2" AS "B(v/2,v/2)" FROM t2, t_params
)
SELECT 
    "n1" AS "標本数1",
    "avg1" AS "平均1",
    "n2" AS "標本数2",
    "avg2" AS "平均2",
    "v" AS "自由度",
    "t_sign" * "t_abs" AS "t値",
    (1.0 - ("Bz(v/2,v/2)" / "B(v/2,v/2)")) * 2.0 AS "p値"
FROM t_bz, t_b1, t_input, t_samples_summary

実行結果

感想

• 値の範囲にもよりますが、手元で試した限りでは小数点以下5~10桁程度の精度は実現しているので、それなりに実用的なものができたと思います。nを増やせば精度は上がります。
• PostgreSQLの再帰（WITH RECURSIVE）やFILTER句など、存在は把握していても実際に使う場面が思いつかなかった機能をうまく使えたのがなんだか嬉しいです。
• 信頼区間の推定に必要な、累積分布関数の逆関数が欲しい場合は全く異なる実装が必要なようです。これは次の課題です。
• 人生で初めてTeXを書きましたが、Qiitaのエディタが優秀なので書いていて楽しかったです。

参考記事

• 実装と数式については、こちらのPascalによるt分布の実装を大変参考にさせていただきました。
• 超幾何級数の説明としては、こちらの記事が分かりやすいです。
• Wikipedia t分布
• PostgreSQL 再帰クエリ