LoginSignup
0
0

More than 1 year has passed since last update.

@morinota(morinota)

Matrix Factorizationって何ぞや?Explicitデータに対するALS

Last updated at Posted at 2022-03-30

はじめに

1 年前に Kaggle に登録しましたが、今回初 Competition として、「H&M Personalized Fashion Recommendations」に参加してみようと思いました(1 ヶ月おくれですが笑)。
データセットはテーブルデータを基本としているようで、画像データやテキストデータに疎い私の様な人にも比較的取っつきやすい気がします。
また、**最終的な成果物(提出物)が"顧客へのレコメンド"**という点がよりビジネス的というか、実務(?)に近いような気がする(一学生の偏見かもしれません笑)ので、個人的に楽しみです：）

今回は、レコメンドエンジンにおける一手法の「協調フィルタリング」、の一手法である行列分解(Matrix Factorization)について自分なりにまとめます。また、行列分解のアルゴリズムの 1 つである ALS(Alternate Least Squares)についても理論をまとめ、スクラッチ実装してみます。

ざっくり調べただけなので恐らく正確ではありませんが、レコメンド手法の樹形図みたいなものを作成してみました。
行列分解(Matrix Factorization)は右下にありますね。
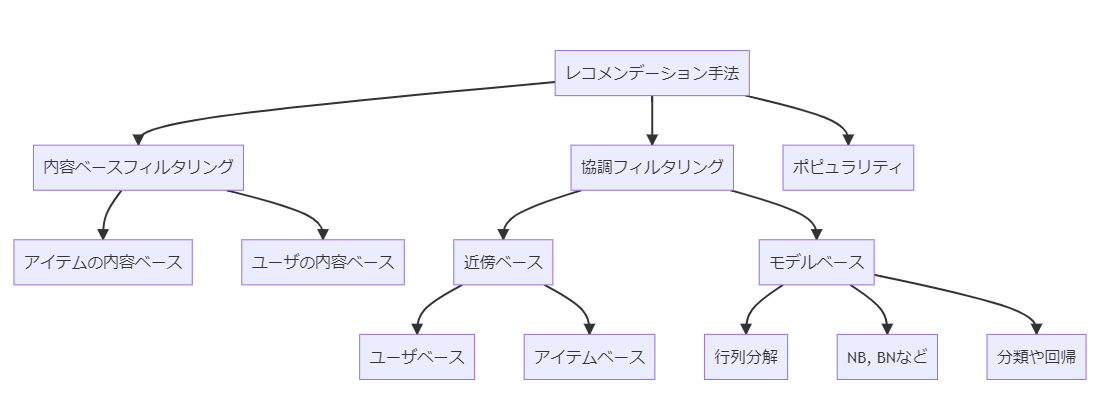
image.png

行列分解(Matrix Factorization, MF)って何ぞや？

行列分解とは、アイテムに対するユーザーの評価値を行列にした評価値行列を、各ユーザーのベクトルからなるユーザー行列と、各アイテムのベクトルからなるアイテム行列の積に分解することを意味します。
(本文では)
行列分解がやっている事を数式にすると以下です。

$$
X \approx W^T \cdot H = \hat{X}
$$

$$
X, \hat{X} \in R^{m\times n}, W \in R^{k\times m}, H\in R^{k \times m}
$$

ここで、

  • m はユニークなユーザの数。n はユニークなアイテムの数。
  • X は行がユーザ、列がアイテムである評価行列(Rating Matrix)。
    • 行インデックス i と列インデックス j がそれぞれ一人のユーザ、1 個のアイテムと対応。
    • 行列の$i, j$成分の値$x_{i, j}$は、ユーザ i がアイテム j に対して下した評価(explixit データの場合)
  • W は行がユーザ、列が潜在変数であるユーザ行列。
  • H は行がアイテム、列が潜在変数であるアイテム行列。
  • k は、指定された潜在変数の数。

行列分解では、潜在変数の個数(=グルーピングの数)k を与えた時、評価行列 X を W と H の積に分解します。
正確には、X にできる限り近い(近似した)$\hat{X}=W^T\cdot H$を推定しています。

得られた$\hat{X}$によって、ユーザがまだ評価していないアイテムの評価値(Explicit データの場合)を予測したり、ユーザの好みを定量化する事ができます。
元々の評価行列$X$ではゼロ(=未評価)だった要素が、推定された$\hat{X}$では補完されているイメージですかね！(Explicit データの場合！)

また、評価行列の推定値$\hat{X}$の各要素(=ユーザ u によって得られるアイテム u の評価)は以下の様に、$W_u$(＝行ベクトル)と$H_i^T$(＝列ベクトル)の内積として表せますね。

$$
\hat{x}{u, i} = \mathbf{w}u^T \cdot \mathbf{h}i \
= \sum{f=0}^{k}{w{u, f} h{f, i}}
$$

ここで、

  • $\mathbf{w}_u^T, \mathbf{h}_i \in R^{k\times 1}$(長さ k の列ベクトル)。
  • $w_{u, f}, h_{i, f}$:それぞれ $\mathbf{w}_u$及び$\mathbf{h}_i$の f 番目の要素。

行列分解における目的関数

さて、行列分解を実施する、言い換えれば、$X \approx W^T \cdot H = \hat{X}$を満たす$W$と$H$を推定する為の目的関数を上の式から考えると、「真の評価行列と推定された評価行列の誤差を最小限に抑えること」って思ってしまいます。この場合にパッと思いつく、最小化したい目的関数(誤差関数)は、

$$
\argmin_{H, W}||X-\hat{X}|| \
= \argmin_{H, W}||X-W^T\cdot H||
$$

ですね。もしくは絶対値は扱いづらいので、二乗して

$$
\argmin_{H, W}(X-\hat{X})^2 \
= \argmin_{H, W}(X-W^T\cdot H)^2
$$

でしょうか。しかし実際にこれらの目的関数で最小化してしまうと、評価行列$X$のゼロ要素(=)もゼロに近い値で推定されてしまいます。
あれ、元々の評価行列$X$ではゼロ(=未評価)だった要素が、$\hat{X}$でもゼロに近い値だったら、そのユーザの好みを予測できませんね...。

つまりレコメンデーションタスクでの行列分解における目的は、「評価行列$X$を正確に近似できるような、$W^T \cdot H = \hat{X}$を推定する」事ではなく、「評価行列$X$におけるゼロ要素(=未評価、穴あきの箇所)を補完(予測)できるような、$W^T \cdot H = \hat{X}$を推定する」ことなんですよね！

なので、レコメンデーションでの行列分解(Matrix Factorization)における目的関数は以下の様になります。

$$
Loss = \sum_{(u,i) \in I} (x_{ui} - \mathbf{w}_u^T \mathbf{h}_i)^2
$$

ここで$I$は評価行列における非ゼロ要素の index の集合です。
つまり、評価行列$X$の非ゼロ要素のみを対象に、$\hat{X}$との誤差を最小化していく、という事ですね！
そうすれば、評価行列$X$におけるゼロ要素は、$\hat{X}$ではゼロに近い値にはなりません。これにより、評価行列では未知だった、「あるユーザの、未評価のあるアイテムに対する嗜好度合い」が予測できそうですね！

なお、実際の行列分解アルゴリズム(ex.ALS)では、上式の二乗和誤差に正則化項(ALS の場合は L2 正則化項)を加えたものを目的変数とします。

まとめると、「W と H の各列ベクトル」、言い換えれば「各ユーザ、各アイテムに対する$\mathbf{w}_u$及び$\mathbf{h}_i$」を既知の評価値(疎行列 X の非ゼロ要素)から学習するのが 行列分解(Matrix Factrozation)であるようです。

ALS（交互最小二乗法、Alternating Least Square）アルゴリズムの理論:

行列分解(行列因数分解)アルゴリズムで、最も有名なものの 1 つが ALS（Alternating Least Squares, 交互最小二乗法）です。

ALS を用いた行列分解における目的関数は、以下の通りです。

$$
Loss = \sum_{(u,i) \in I} (x_{ui} - \mathbf{w}u^T \mathbf{h}i)^2 + L2\
= \sum{(u,i) \in I} (x{ui} - \mathbf{w}_u^T \mathbf{h}i)^2 + \lambda \Biggl(\sum_u n{w_u}|\mathbf{w}u|^2 + \sum_i n{h_i}|\mathbf{h}_i|^2\Biggr)
$$

ALS では、L2 正則化項が追加されていますね。ここで、

  • $I ：評価値が格納されているインデックスの集合。$
  • $ x_{u, i}：評価行列 X の u 行目 i 列目の要素。$
  • $ \lambda：正則化項の強さを指定する値(ハイパラ?)$
  • $ n_{w_u}：I の u 行のランク(=ユーザ u が評価したアイテムの数)$
  • $ n_{h_i}：I の i 行のランク(=アイテム i を評価したユーザの数)$

また、ALS では2 つの目的関数を交互に最小化し、2種のパラメータを交互に更新します。

  • 最初にユーザ行列を固定し、アイテム行列の値$H$を更新。
  • 次にアイテム行列を固定し、ユーザ行列の値$W$を更新。

これを繰り返します。
目的関数を最小化するパラメータを探す為の更新式は以下の通りです。

  • $$ e_{u, i} = x_{u, i}-\mathbf{w_u}^T \mathbf{h_i} $$
  • $$ w'{u, k}= w{u, k} + 2 \times \alpha \cdot e_{u, i} \cdot h_{k, i}$$
  • $$ h'{i, k}= h{u, k} + 2 \times \alpha \cdot e_{u, i} \cdot w_{u, k}$$

学習率$\alpha$の勾配降下法かな？
$\alpha$以降は、目的関数を各パラメータで一回微分したら出てきそう...な気がしますね。また時間があれば導出してみようと思います：）

ALSによるExplicitデータの行列分解をスクラッチ実装

以下、コードになります。
とはいっても、https://qiita.com/ysekky/items/c81ff24da0390a74fc6c 様の記事を読みながら、自分でコメントアウトを大量に挟みつつ、真似して書いただけです！笑
(関数の説明文を最近書くようにしてみているのですが、書き方がおかしかったらすいません笑　指摘していただければ喜びます：）)

from distutils.log import error
from tkinter import W
import numpy as np
import numpy


def get_rating_error(x, w, h):
    '''
    行列内の各要素の誤差の値を計算する関数

    parameters
    ------------
    x: 評価行列Xの各要素X_ui
    w:ユーザ行列Wのu列目(列ベクトル)
    h:アイテム行列Hのi列目(列ベクトル)

    Return
    ---------
    X_uiとX_ui_hat(wとhの内積)の誤差.
    '''
    return x - numpy.dot(w, h)


def get_error(X: np.ndarray, W: np.ndarray, H: np.ndarray, beta):
    '''
    ALSによる行列分解における誤差関数の値を計算する関数

    parameters
    -----------
    X:観測された評価行列.
    W:ユーザ行列(潜在変数×ユーザ)
    H:アイテム行列(潜在変数×アイテム)
    beta:L2正則化における罰則項のハイパーパラメータlambda

    Return
    -------
    ALSによる行列分解における目的関数(誤差関数)の値.
    '''
    # 目的関数(誤差関数)の初期値(数式のΣ)
    error = 0.0
    # 2重(各アイテム、各ユーザ)のforループでXの各要素に対して処理を実行する.
    for u in range(len(X)):
        for i in range(len(X[u])):
            # もし要素がゼロなら
            if X[u][i] == 0:
                # 次のループ処理へ
                continue
            # 目的関数(誤差関数)へ、2乗和誤差の足し合わせ
            # pow()関数はべき乗を計算する関数
            error += pow(get_rating_error(x=X[u][i], w=W[:, u], h=H[:, i]), 2)

    # 全ての要素で誤差を計算=>2乗和誤差を算出し終えたら...
    # L2正則化項を追加
    # np.linalg.norm()関数:行列やベクトルのノルム(原点からの距離)を計算する関数
    error += beta/2.0 * (np.linalg.norm(x=W, ord=2) +
                         np.linalg.norm(x=H, ord=2))
    return error


def matrix_factorization(X: np.ndarray, len_of_latest_variable, steps=5000, alpha=0.0002, beta=0.02, threshold=0.001):
    '''
    ALSによる行列分解を実行する関数

    parameters
    -----------
    X:実際に観測された評価行列.
    len_of_latest_variable:潜在変数の数.
    alpha:勾配降下法の学習率
    beta:L2正則化における罰則項のハイパーパラメータlambda
    threshold:学習を終了するかどうかを判定する、誤差関数の値の閾値.

    Return
    -----------
    分解されたユーザ行列W(潜在変数×ユーザ)とアイテム行列H(潜在変数×アイテム)
    '''

    # WとHの初期値を設定
    W = np.random.rand(len_of_latest_variable, len(X))
    H = np.random.rand(len_of_latest_variable, len(X[0]))

    # ループ処理でパラメータ更新を繰り返していく
    for step in range(steps):
        # 2重(各アイテム、各ユーザ)のforループでXの各要素に対して処理を実行する.
        for u in range(len(X)):
            for i in range(len(X[u])):
                # もし要素がゼロなら
                if X[u][i] == 0:
                    # 次のループ処理へ
                    continue
                # 更新に必要なeを求める
                err = get_rating_error(x=X[u][i], w=W[:, u], h=H[:, i])
                # 行列WとHの、X_uiに関わる要素の更新
                for k in range(len_of_latest_variable):
                    W[k][u] += alpha * (2 * err * H[k][i])
                    H[k][i] += alpha * (2 * err * W[k][u])

        # 更新後の目的関数(誤差関数)の値を確認
        error = get_error(X, W, H, beta)
        # 誤差関数の値が、設定した閾値を下回っていれば...
        if error < threshold:
            break

    return W, H


def main():
    # サンプルの評価行列を生成
    X = numpy.array([
        [5, 3, 0, 1],
        [4, 0, 0, 1],
        [1, 1, 0, 5],
        [1, 0, 0, 4],
        [0, 1, 5, 4],
    ]
    )

    # 行列分解
    W_hat, H_hat = matrix_factorization(X, len_of_latest_variable=2)
    # WとHから、Xの推定値X\hatを生成.
    X_hat = np.dot(a=W_hat.T, b=H_hat)
    print(X_hat)


if __name__ == '__main__':
    main()

おわりに

今回の記事では、レコメンドエンジンにおける一手法の「協調フィルタリング」、の一手法である行列分解(Matrix Factorization)について、自分なりにまとめてみました。また、行列分解のアルゴリズムの 1 つである ALS(Alternate Least Squares)についても理論をまとめ、スクラッチ実装してみました。

実際に自分で数式を記述したりスクラッチ実装したりしてみると、理解しやすい気がします！やって良かったですね：）
今回、Explicit データの評価行列に対する行列分解の流れが何となく掴めた気がします。
次回は、Implicitデータの評価行列に対する行列分解について勉強しようと思います！H&M Personalized Fashion RecommendationsはImplicitデータですし！

参考

以下の記事を参考にさせていただきました！良記事有り難うございました！

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0