n週連続推薦システム系 論文読んだシリーズ28週目: (RecSys2023の論文を読むために!)Sequential推薦にはuni-directionalではなくbi-directionalなモデルが適しているぞ!というBERT4Recの論文を読んだ

BERT4Rec: Sequential Recommendation with Bidirectional Encoder Representations from Transformer

published date: 21 August 2019,
authors: Fei Sun, Jun Liu, Jian Wu, Changhua Pei, Xiao Lin, Wenwu Ou, Peng Jiang
url(paper): https://arxiv.org/abs/1904.06690
(勉強会発表者: morinota)

---

どんなもの?

• RecSys2023のAmazonのBERT4Recを継承した事前学習済み推薦モデルの論文が読みたかったので、先に読んでみた。
• Amazonの2019年のbi-directionalなSequential推薦モデル BERT4Rec を提案した論文。
• sequential推薦タスクにおけるいくつかのベンチマークデータセットで、当時のSOTAを達成。
• Transformer Encoderのモデルアーキテクチャや、既存研究との関連性も丁寧に述べてくれていて、長いけど有り難い論文だった感。

先行研究と比べて何がすごい?

Sequential推薦についての説明:

• ユーザの興味を正確に把握する事は、効果的な推薦システムを作る上で重要。
• しかし多くの実世界のアプリケーションでは、ユーザの現在の興味は、過去の過去の行動に影響され、本質的にdynamicでevolivingである。
• このようなdynamicに変化するユーザの興味をモデル化する為に、ユーザの過去のinteractionsに基づいてsequentialな推薦を行う手法が提案 = Sequential推薦。

Sequential推薦の既存研究における、手法の発展の流れ:

手法の発展の流れは以下の様な感じ

• マルコフ連鎖モデルを活用(推薦を逐次最適化問題とみなす)
• -> MF(=協調フィルタリング手法の一つ)とMCモデルの合せ技(Factorizing Personalized Markov Chains, etc.)
• -> RNN系手法(ex. GRU4Rec, DREAM, user-based GRU, attention-based GRU, etc. )やCNN系手法(ex. Carser)で、ユーザ行動履歴をベクトル(=user preference representation)にencode
  • GRU4RECやCaserは他のsequential recommenderの論文のベースラインとして出てきた気がする
  • attenitionメカニズムをオリジナルモデルのattitional componentとして採用する手法も出てきてる。
• -> self-attentionに基づく手法(ex. SASRec)
  • (SASRecはself-attentionを使ったsequential recommenderで有名なやつ! Transformter decoderを使った手法で、本論文時点でいくつかのベンチマークデータセットでSOTAを達成してる)
• しかし、上記の既存研究はいずれも、uni-directionlな(left-to-rightな)sequentialモデルである。

Sequential推薦はuni-directionlモデルは最適ではないという話

• 本論文では、以下の２つの制限から、uni-directionalなモデルは逐次推薦タスクに適したuser preference表現を学習するには不十分であると主張。
  • 制限1: uni-directionalなモデルでは、各interactionがそれよりも過去のinteractionsからの情報しか考慮できないため、hidden representationの品質が制限される。
  • 制限2: uni-directionalなモデルは、**rigid order assumption (厳密な順序の仮定??)**を満たすテキストデータや時系列データ等には有効。しかし、実アプリケーション上のユーザ行動は必ずしもその仮定を満たさない。
    • (テキストや時系列データと比べて、実アプリケーション上のユーザ行動は、Sequence内のノイズがとても多く含まれているから、ridgidly ordered sequenceを前提としたuni-directionalなモデルは最適ではない、みたいな話かな)
• よって本論文では、uni-directionalではなくbi-directionalなモデル(要はBERTのような bi-directional self-attention model)を採用したBERT4Recを提案し、Sequential推薦タスクにより適したuser preference 表現の学習を目指す。
  • モデルの学習には、Clozeタスク(=要は、BERTの事前学習タスクの1つ、masked-item-predictionの認識)を採用。

技術や手法の肝は？

BERT4Recのモデルアーキテクチャ

(論文より引用)

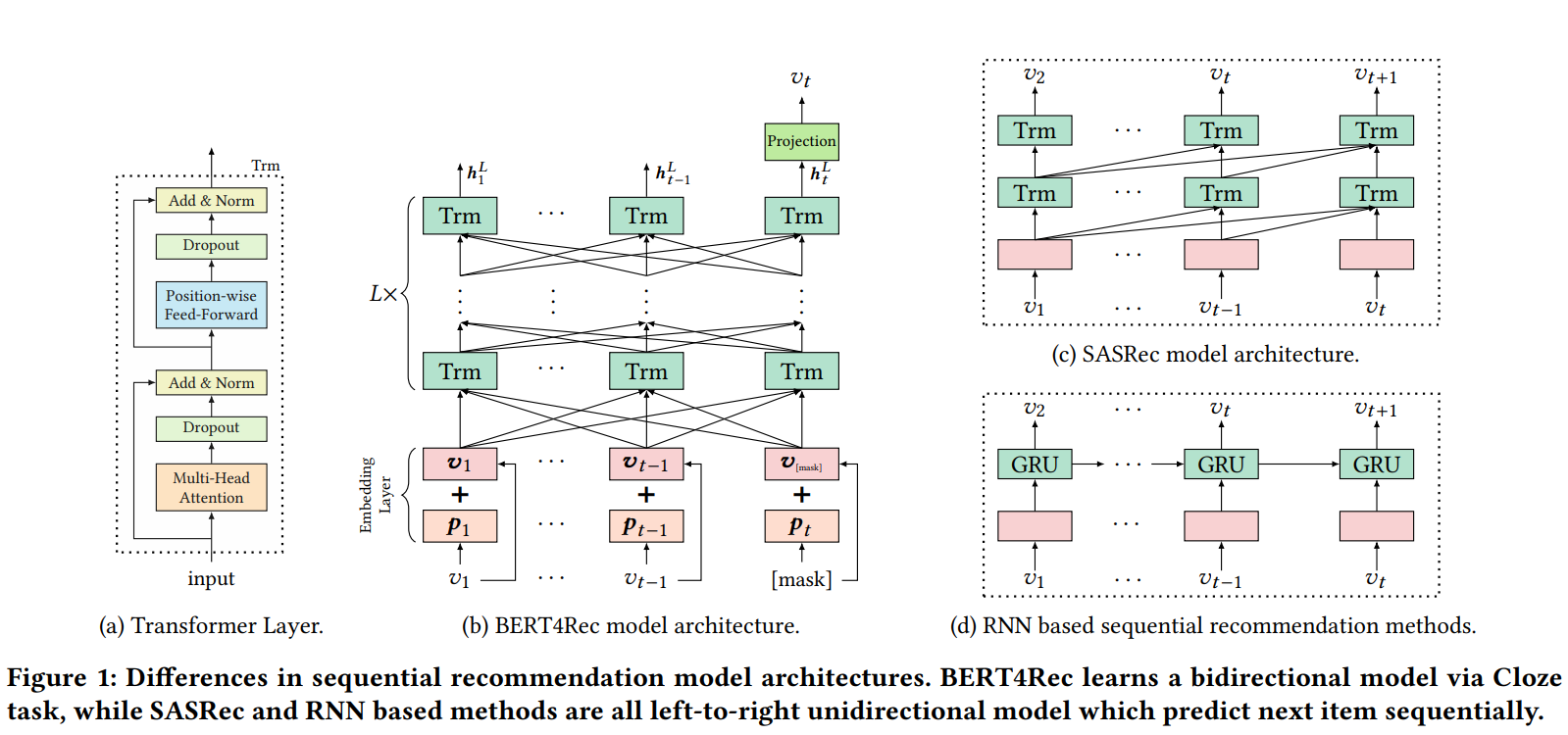
• BERT4Recは、図1bの様に $L$ 個のTransformer層(ブロック?)を重ねた Transformer Encoder で構成される。(要はBERTと同じモデルアーキテクチャ)
• 図1dのRNNベースの手法との違い:
  • 図1dのRNNベースの手法ではsequence内の各位置の情報を段階的に前方に伝えて学習させる。一方で図1bのBERT4Recや図1cのSASRecのような self-attention ベースの手法はsequence内の各位置の情報を直接補足する。
  • またRNNベースの手法と比較してself-attentionは並列化が簡単。
• 図1cのSASRecとの違い:
  • 同じself-attentionベースの手法でも、SASRecはleft-to-rightなuni-directionalなself-attentionを採用しており、BERT4Recはbi-directionalなself-attentionを採用している。

以下で、Transformerブロックの説明をまとめておく(論文にも書かれてたので復習も兼ねて!)

Transformer layer (Block?)

• 図1bに示す様に、長さ $t$ の入力sequenceが与えられると、Transformer層の適用によって、sequence内の各position $i$ に対して、各Transformer層 $l$ で hidden representation $\mathbf{h}^{l}_{i}$ を計算する。
  • $\mathbf{h}^{l}_{i} \in \mathbb{R}^{d}$ を積み重ねた行列を $\mathbf{H}^{l} \in \mathbb{R}^{t \times d}$ と表記。
• 図1aに示す様に、Transformer層 ($Trm$ と表記) は 2つのsub layersを含む: Multi-Head Self-Attention 層 ($MH$ と表記)と Position-wise Feed-Forward Network 層($PFFN$ と表記)。

Multi-Head Self-Attention 層

• attentionメカニズムは、様々なタスクにおける sequence modeling の不可欠な要素。sequence内の距離に関係なく、ペア間の依存関係を捉えることができる。
• 既存研究から、異なる位置にある異なるrepresentation subspaces(表現部分空間?)からの情報に共同で注意を向けることが有益である事が示されている為、単一のattentionよりもmulti-head attentionが採用される事が多い。(これがmulti-head attetionを採用する理由なのか...!)
• multi-head attentionの振る舞い:
  • まず、入力表現 $\mathbf{H}^{l}$ を学習可能な異なる $h$ 個のlinear projection層 (i.e. 3h個の投影行列)に通して、$h$ 個の部分空間に線形投影する。($l$ 番目の隠れ表現が入力ってことは、$l+1$ 番目のTransformerブロクを想定してる??)
  • 次に、$h$ 個のself-attetion関数を並列に適用して $h$ 個の出力表現を生成する。
  • 最後に、$h$ 個の出力表現を連結した上で、1個のlinear projection層に通し、最終的な出力表現 $MH(\mathbf{H}^{l})$ を得る。

MH(\mathbf{H}^l) = [head_1;head_2; \cdots, ;head_{h}] \mathbf{W}^{O}

head_i = Attention(\mathbf{H}^l \mathbf{W}^Q_{i}, \mathbf{H}^l \mathbf{W}^K_{i}, \mathbf{H}^l \mathbf{W}^V_{i})
\tag{1}

• ここで、各headの投影行列 $\mathbf{W}^Q_i \in \mathbb{R}^{d × d/h}$, $\mathbf{W}^K_i \in \mathbb{R}^{d × d/h}$, $\mathbf{W}^V_i \in \mathbb{R}^{d × d/h}$ と、全headの出力表現を結合したあとに通す投影行列 $\mathbf{W}^O \in \mathbb{R}^{d×d}$ は学習可能なパラメータ。

  • (注意: ここの添字 $i$ はsequence内のpositionではなく、各headを識別する為の添字!)
  • (注意: 各Transformer層で、これらの投影行列は共有していない! 簡略化の為に省略しているが、実際には添字 $l$ が付く!)

• $Attention$ 関数にはScaled Dot-Product Attentionを採用:

$$
Attention(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = softmax(\frac{QK^T}{\sqrt{d/h}}) V
\tag{2}
$$

• ここで、Query $\mathbf{Q}$、Key $\mathbf{K}$、Value $\mathbf{V}$ は、各headの投影行列によって同じ行列 $\mathbf{H}^l$ から線形投影されるもの。
• 温度 $\sqrt{d/h}$ は、極端に小さな勾配を避けるために、よりソフトなattention分布を作り出すために導入されている[16, 52]。(うんうん、Transformer論文でやったやつ。softmax関数の温度パラメータみたいな...!)

Position-wise Feed-Forward Network 層

• 上述した通り、self-attentionサブレイヤーは主に線形投影(linear projection)に基づいている。(このパートだけだと線形モデル...!)
  • -> モデルに非線形性と、異なる次元間(=$d$ 次元の隠れ表現の各次元の意味!)の相互作用を持たせるために、self-attentionサブレイヤーの出力に対して、PFFNを適用する。
  • (Position-wise = sequence内の各positionで別々に、かつ同一に!)
• PFFNは、2つのアフィン変換と、その間のGELU(Gaussian Error Linear Unit)活性化関数からなる。
  • (アフィン変換 = 線形変換と平行移動の組み合わせによる図形や形状の変形方法らしい...! 要は重みを乗じてbias項を足す、って話か!)
  • (GELU活性化関数: Gaussianなので正規分布の累積分布関数を使って入力を0 ~ 1の範囲に滑らかにするやつっぽい。じゃあ形はsigmoid関数と似てそう??) (BERTとOpenAI GPTの論文に従って採用したらしい。)

$$
PFFN(\mathbf{H}^l) = [FFN(\mathbf{h}^l_1)^T; \cdots; FFN(\mathbf{h}^l_t)^T]^T
$$

$$
FFN(\mathbf{x}) = GELU(\mathbf{x}\mathbf{W}^1 + \mathbf{b}^1)\mathbf{W}^2 + \mathbf{b}^2
$$

$$
GELU(x) = x \Phi(x)
\tag{3}
$$

• ここで、$\Phi(x)$ は標準ガウス分布の累積分布関数。
• $W^(1) \in \mathbb{R}^{d \times 4d}$, $W^(2) \in \mathbb{R}^{4d×\times d}$, $\mathbf{b}^(1) \in \mathbb{R}^{4d}$ および $\mathbf{b}^(2) \in \mathbb{R}^{d}$ は学習可能なパラメータであり、すべてのposition(=sequence内のposition $1 ~ t$!!)で共有される(=これがPosition-wiseな点!)。
• (注意: 各Transformer層でこれらのパラメータは共有していない! 簡略化の為に省略しているが、実際には添字 $l$ が付く!)

サブレイヤー間の接続

• self-attentionのレイヤーを重ねる事で、より複雑な表現を学習できる。しかし、ネットワークが深くなるにつれて学習が難しくなる。
• そこで図1aのような工夫を行う:
  • 2つのサブレイヤーそれぞれの周囲に**残差接続(residual connection)[9]**を採用。
  • **レイヤー正規化[1]**を使用し、同じレイヤーにあるすべての隠れユニットの入力を正規化する(大きさを揃えるってこと??)。
  • 正規化する前に、各サブレイヤーの出力にドロップアウトを適用。
• よって、各サブレイヤーの出力は $LN(x + Dropout(sublayer(x)))$ となる.
  • $sublayer(\cdot)$ はサブレイヤー自身の関数。$LN$ はレイヤー正規化関数。
  • (3つの工夫が何もない場合は、出力は $sublayer(x)$ だけになるはず。じゃあ $x$ を足しているのがresidual connectionなのか )
• 要するに、BERT4Rec は各層の隠れ表現を以下のように洗練する:

$$
\mathbf{H}^{l} = Trm(\mathbf{H}^{l-1}), \forall i \in [1, \cdots, L]
\tag{4}
$$

(↑前のTransformerブロックの出力が、次のTransformerブロックの入力になる)

$$
Trm(\mathbf{H}^{l-1}) = LN(A^{l-1} + Dropout(PFFN(A^{l-1})))
\tag{5}
$$

(↑PFFNサブレイヤーの出力表現に、DropoutとResidual Connectionとレイヤー正規化を適用したものが、ある1つのTransformerブロックの出力表現になる。)

$$
A^{l-1} = LN(\mathbf{H}^{l} + Dropout(MH(\mathbf{H}^{l-1})))
\tag{6}
$$

(↑MHサブレイヤーの出力表現に、DropoutとResidual Connectionとレイヤー正規化を適用したものが、PFFNサブレイヤーへの入力表現になる)

Embedding LayerとPositional Embeddingの話

• RNNやCNNと異なり、attention自体は入力sequenceの順序を意識しない。
• だからpositional embeddingが必要!
• 与えられたitem $v_i$ に対して、その入力表現 $\mathbf{h}^{0}_{i}$ は、対応するitem埋め込みと位置埋め込みを合計することによって構築される。

\mathbf{h}^{0}_{i}= \mathbf{v}_{i} + \mathbf{p}_{i}

• ここで、$\mathbf{v}_i \in \mathbf{E}$ はitem $v_i$ の $d$ 次元埋め込み、$\mathbf{p}_i \in \mathbf{P}$ はposition index $i$ の$d$ 次元位置埋め込み。
• BERT4Recでは、より良い性能を得るために、固定正弦波埋め込みに代えて、学習可能な位置埋め込みを採用しているらしい。

Output Layerの話

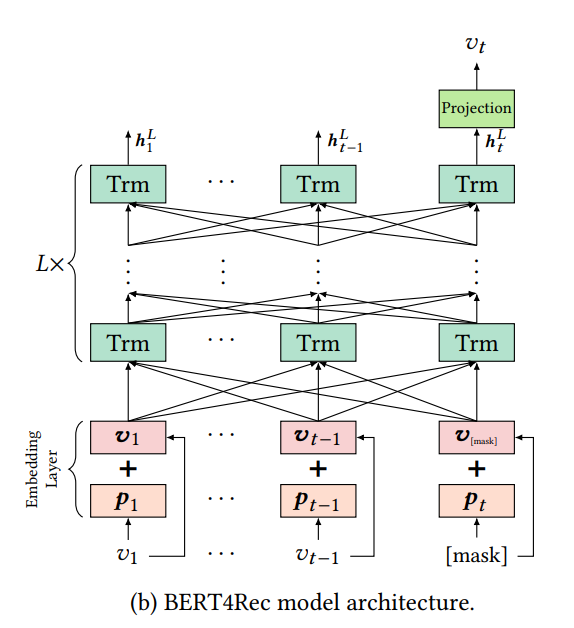
(論文より引用)

• L個のTransformerブロックの後、入力sequenceのすべてのpositionのitemに対する最終的な出力表現 $\mathbf{H}^{L}$ が得られる。
• 図1bに示すように、マスクされたアイテム $v_t$ (i.e. $v_{[mask]}$) の出力表現 $\mathbf{h}^L_t$ に基づいて、time step $t$ のアイテムを予測する。
  • 入力sequenceの最後尾に $v_{[mask]}$ を追加するのはBERT4Recの推論の為の工夫!
• 具体的には、GELU活性化関数を挟んだ2層のFFNを適用し、推薦候補アイテムに対する出力分布(=確率質量関数みたいなやつ!)を生成する:

$$
P(v) = softmax(GELU(\mathbf{h}^L_{t} W^P + \mathbf{b}^P) \mathbf{E}^T + \mathbf{b}^O)
\tag{7}
$$

• ここで、$W^P$ は学習可能な投影行列、$b^P$ と $b^O$ はbias項である。
• $\mathbf{E} \in \mathbb{R}^{|V|\times d}$ は推薦候補アイテム集合 $V$ の埋め込み行列。
  • BERT4Recでは、overfittingを緩和し、モデルサイズを小さくするために、入力層と出力層で共有item埋め込み行列を使用する。($\mathbf{E}$ は基本的にはSequential推薦とは共同で学習しないような、固定値なのかな 入力層と出力層で同じパラメータを使うと言っているだけで、一緒に学習する想定なのかな。)

BERT4Recの学習(Clozeタスクについて)

• bi-directionalなモデルなので、next-item-predictionタスクが有効でない話:

  • RNNやSASRec等のuni-directionalなSequential推薦モデルは、図1cや図1dの様に、入力Sequenceの各positionに対してnext-item-predictionタスクを学習させるのが一般的。
  • ex) 入力sequence $[v_1, \cdots ,v_t]$ のターゲットは、シンプルにshiftされた $[v_2, \cdots, v_{t+1}]$ になる。
  • その一方で、bi-directionalなモデルであるBERT4Recは、これは非常に簡単なタスクとなり、学習が意味をなさない。(双方向なので未来の情報を使えてしまうので! 無意味なパラメータに最適化されてしまう!)

• BERT4Recを効率的に学習させる為に、新しい学習タスクとしてClozeタスクを適用する (i.e. Masked Language Model。要はmasked-item-predictionってことか!) (BERTの事前学習タスクの一つ!)

  • まず各学習stepにおいて、入力sequenceの全itemのうち $\rho$ の割合をランダムにmaskする。(i.e. 特別なトークン"[mask]"で置き換える)
  • 次に、maskされたitemの元のIDを、その左右のcontextのみに基づいて予測する。

• 例えば以下。

$$
Input : [v_1, v_2, v_3, v_4, v_5] \rightarrow^{randomly_mask} [v_1, [mask]_1, v_3, [mask]_2, v_5]
$$

$$
\
Labels:[mask]_1 = v_2, [mask]_2 = v_4
$$

• “[mask]”に対応する最終的な隠れ表現は、従来のSequential推薦と同様に、推薦候補アイテム集合に対する出力ソフトマックスに供給される。
• 最終的に、mask済みの入力Sequence $\mathcal{S}'_{u}$ (=あるユーザ $u$ の一部mask済みの行動sequence) に対する損失を、maskされたターゲットの負の対数尤度として定義する(これがClozeタスクの損失関数):

\mathcal{L}
= \frac{1}{|\mathcal{S}^m_u|}
\sum_{v_m \in \mathcal{S}^m_u} - log P(v_m = v^{*}_{m}|\mathcal{S}'_{u})
\tag{8}

• ここで、

  • $\mathcal{S}'_{u}$ は、あるユーザ $u$ の行動sequence $\mathcal{S}_u$ の一部がmaskされたversion。
  • $\mathcal{S}^{m}_{u}$ は、その中のランダムにmaskされたitem集合。
  • $v^{*}_{m}$ は、maskされたitem $v_m$ の真のitem。
  • 確率 $P(\cdot)$ は式(7)で定義したやつ。

Clozeタスクの利点

• モデルを訓練するためのサンプルをより多く生成できること(ランダムにmaskするから??)
• 長さ $n$ の入力sequenceを想定すると...
  • 従来のnext-item-predictionタスクを学習させる場合は、学習用に $n$ 個のユニークなサンプルが生成される。(epoch毎に学習サンプルは基本同じ?)
  • BERT4Recのようなmasked-item-predictionタスクを学習させる場合、複数回のepochで、nCk 個のサンプルを得られる。(ランダムに$k$ 個のitemをmaskする場合)

BERT4Recの推論

• Clozeタスクの欠点: 最終タスクと整合性がない事。
  • BERT4Recの学習はmasked-item-predictionで行うのに対し、実アプリケーション上で運用させたいのはnext-item-predictionであり、学習と最終的なusecaseの間にミスマッチが生じる。
  • (うんうん、代理学習問題的な??)
• 対応策:
  • 推論時は、ユーザの行動sequenceの最後尾に特別なtoken “[mask]” を追加し、このtokenの最終的な隠れ表現 $\mathbf{h}{t} = \mathbf{h}{[mask]}$ に基づいてnext-itemを予測する。(sequenceの先頭の"[cls]"トークンじゃなくて最後尾なんだ...!!)
  • 学習時にも、ミスマッチを緩和させる為、入力sequenceの最後のitemだけをmaskするサンプルも作り、学習データに含ませる。(このサンプルだけmasked item prediction = next item predictionになるのか...!)
    • これはSequential推薦のfine-tuningのように機能し、推薦性能をさらに向上させることができる。

NLPタスクにおけるBERTと異なる点:

• BERT4Recは、NLPタスクにおけるBERTに関連しているが、いくつか違いがある:
• 違い1: 「BERTはsentence表現の為の事前学習モデルだが、BERT4RecはSequential推薦のためのend-to-endなモデルである」
  • BERT は、タスクに依存しない大規模なコーパスを活用して、様々な下流タスクの為の初期値となるsentence表現モデルを学習する。
• 違い2: 「BERTと比較して、BERT4Recは next-sentence-predictionタスク を学習しない。また segment embeddingを使用しない。」
  • ユーザの過去の行動を1つのsequenceとしてモデル化するので、↑が意味をなさない?

どうやって有効だと検証した?

• 4種のベンチマークデータセットによる、オフライン実験で評価してた。
  • Amazon Beauty
  • Steam
  • MovieLens 1m
  • MovieLens 20m

For all datasets, we convert all numeric ratings or the presence of a review to implicit feedback of 1 (i.e., the user interacted with the item).

各データセットはexplicitなデータだが、やや強引(?)にimplicit feedbackと見做して実験してる感じ...!

• 評価方法:

  • Sequential推薦で広く知られる leave-one-out 評価(i.e., next item recommendation)タスクを採用した。
    • leave-one-out = 各ユーザについて、行動sequenceの最後のitemをテストデータセットとして抜き出し、最後のitemの直前のitemを検証データセットとして扱い、残りのitemを学習に利用する。

• 評価指標:

  • 推薦タスクで一般的なaccuracy-metrics: Hit Ratio (HR), Normalized Discounted Cumulative Gain (NDCG), Mean Reciprocal Rank (MRR), etc.

• ベースラインのモデル:

  • 非パーソナライズ手法: most popular items (POP)
  • パーソナライズ 且つ 非Sequential手法: BPR-MF と NCF (ともに協調フィルタリング手法)
  • パーソナライズ 且つ Sequentialモデル: FPMC (MC系手法), GRU4Rec(RNN系手法), Caser(CNN系手法), SASRec(uni-directionalなself-attention系手法. Sequential推薦のSOTA)

議論はある？

BERT4Rec vs ベースライン手法の推薦性能の比較

(論文より引用)

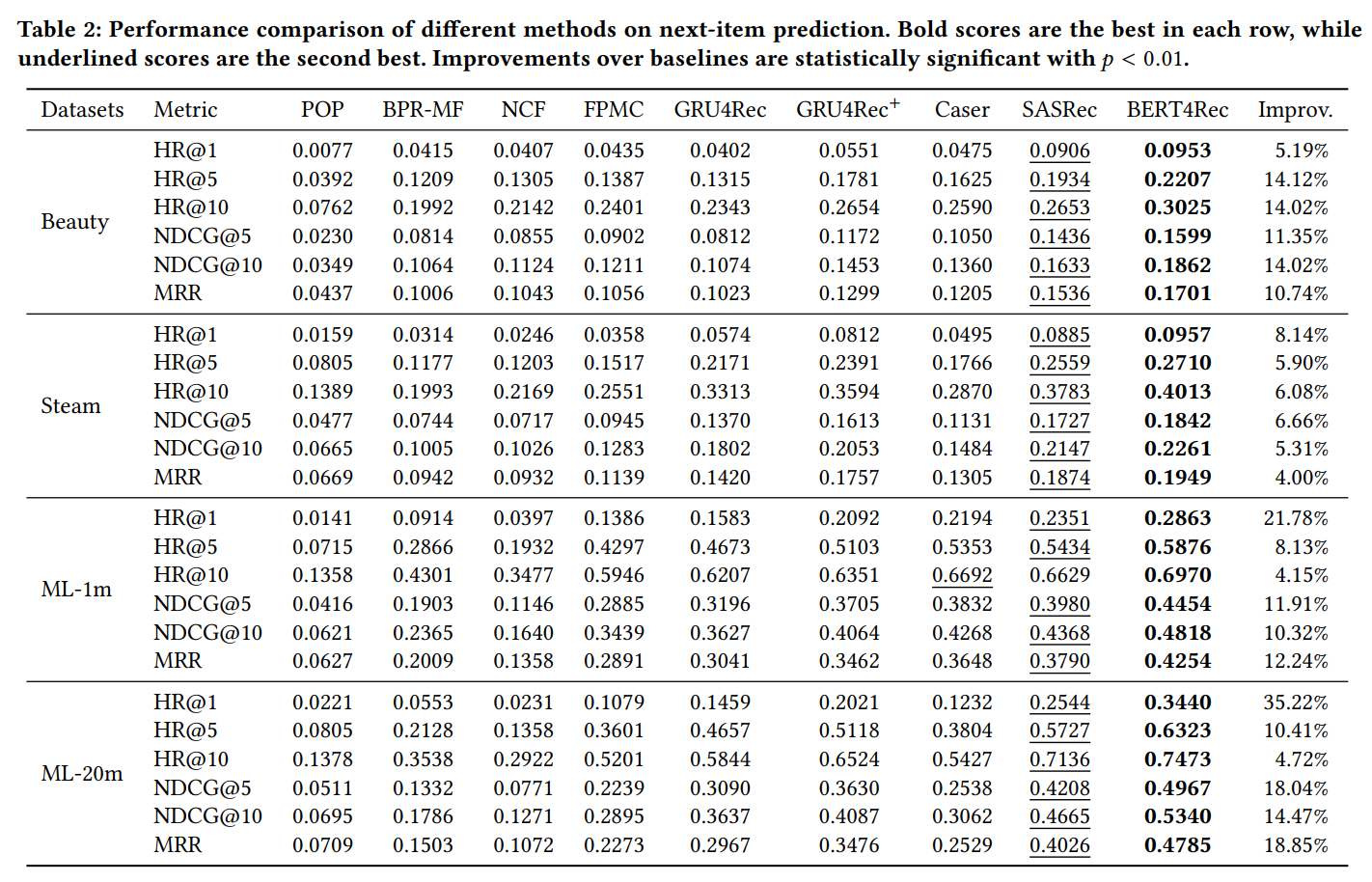
• 表2は、4つのベンチマークデータセットにおける全モデルの最良の結果をまとめたもの。
• 結果1: 非パーソナライズ手法(POP) は、一貫して最低の性能だった。
• 結果2: Sequential手法は、一貫して非Sequential手法を上回る。
  • (まあleave-one-outの評価方法が、Sequenttial手法に有利な評価方法だからだよなぁ...。)
• 結果3: Sequential手法の中で、SASRecは他のMC, RNN, CNN系手法よりも良い結果を示した。
  • ->self-attentionメカニズムは、sequential推薦タスクにおいて有効...!
• 結果4: BERT4Recは、一貫して全ての手法の中で最も優れた結果を示した。
  • sequential推薦タスクbi-directionalなモデルの有効性...!
  • (論文では、BERT4Recの性能の高さはbi-directionalモデルだから? それともClozeタスクを学習させてるから? のablation実験もやってた。)

なぜ、どのようにbi-directionalモデルはuni-directionalモデルよりも性能が良いのか??

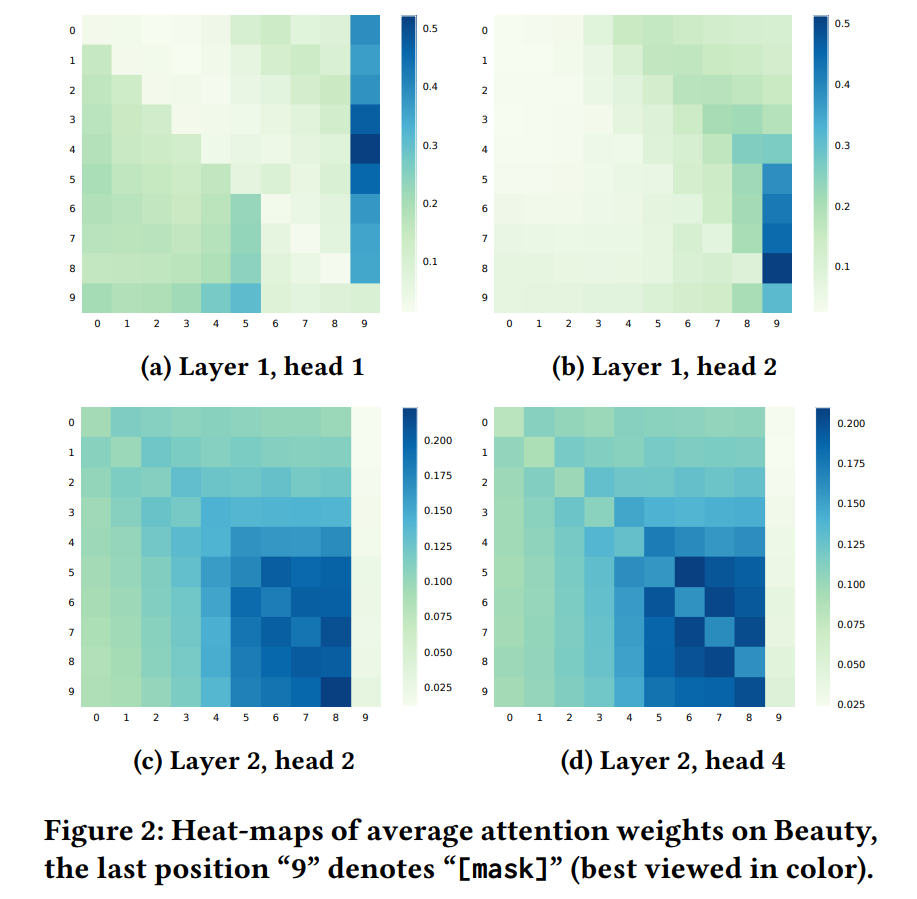
(論文より引用)

• 図2は、Beautyデータセットの実験にて、入力sequenceの最後の10item(=最後のitemは"[mask]"token)の平均attention wwightを可視化したもの。(見解、なんとなくしか分からなかった...!)
• 見解1: attentionは各headによって異なる。
  • ex) 1つ目のTransformer層では、head1は左側のitemに注目し、head2は右側のitemに注目していた。
• 見解2: attentionは各layerによって異なる。
  • ex) 2つ目のTransformer層では、より右側(i.e. 最近の)のitemに注目する傾向がある。
• 見解3: uni-directionalモデルが左側のitemにしかattentionできないのと異なり、BERT4Recのitemは左右両側のitemにattentionする傾向がある。

その他の実験

各種ハイパーパラメータの影響の検証や、モデルアーキテクチャの各componentの影響を調査するablation実験の結果が論文で報告されていた。

• 各種ハイパーパラメータの影響:
  • 隠れ表現の次元数 $d$:
    • モデル性能は、$d$ が大きくなるにつれて収束する傾向にあった。
    • 特に疎なデータセットでは、$d$ を大きくしてもモデル性能は必ずしも工場しなかった。(たぶんoverfittingが原因)
    • 特にBERT4Recの場合は、$d$ が比較的小さい( $d \geq 64$)場合でも、一貫して他のベースラインを上回った。->BERT4Recは $d = 64$ で満足のいく性能を達成できる。(d=64、小さい...! ID-basedの手法はそれくらいで良いのかも...! でも以前、「MFをハイパラチューニングすればdeep系手法にも負けない」旨の論文を見た際には $d =300$ とかにしてた気もする)
  • Clozeタスク学習時のmask比率 $\rho$:
    • mask比率 $\rho$ はモデル学習における重要な要素であり、損失関数(式8)に直接影響する。
    • 全てのケースで、$\rho=0.2$ が $\rho=0.1$ よりも性能が良かった. -> まず $\rho$ は小さすぎてはならない。
    • sequence長が短いデータセットでは $\rho = 0.4 ~0.6$ がベストの性能だった。一方で、長いデータセットでは 小さな $\rho$ (0.2) が適していた。
    • $\rho > 0.6$ の範囲では $\rho$ が大きくなるにつれて性能が低下する一般的なパターンがあった。
  • sequence最大長 $N$:
    • 適切な最大長Nは、データセットの平均配列長に大きく依存する。
    • Nを大きくすると、余分な情報とノイズが増える傾向があるため、Nを大きくしてもモデル性能は必ずしも向上しない。
• ablation実験:
  • positional embedding:
    • PEを削除すると、特にsequence長が長いデータセットにおいて、BERT4Recの性能が劇的に低下した。
  • PFFN:
    • sequence長が長いようなデータセットで特に効果的だった。
  • レイヤー正規化、residual connection, Dropout:
    • これら3つの工夫は、主にoverfittingを緩和する為に導入されたもの。
    • 小さなデータセットで特に有効だった。
  • Transformer層の数 $L$:
    • $L$ を大きくするほど、特に大規模なデータセットで性能を向上できた。
    • (大きくすると言っても、NLPのタスクと異なり、Sequential推薦においては $L = 2$ 前後で十分飽和する、という結果が他の論文で主張してた気がする。本論文でFも $L = 1 ~ 4$ の範囲での実験だし)
  • multi-head attentionのhead数 $h$:
    • sequenceが長いデータセットほど大きな $h$ が有効。
    • multi-head self-attentionで長距離の依存関係を捉えるには、大きなhが不可欠であるという既存研究の経験的な結果と一致。

今後の拡張性:

• 1. BERT4Rec自体は、ID-basedな(ID-onlyな)手法。様々なアイテムの特徴量を組み込む事で表現力の向上が見込める。
• 1. ユーザが複数のセッションを持っている場合、user componentをモデルに導入する事で、ユーザモデリングの能力の向上が見込める。(同一ユーザの複数のsessionの関連性を考慮するって事か...!)

次に読むべき論文は？

• RecSys2023のAmazonのBERT4Recを継承した事前学習済み推薦モデルの論文