活性化関数とは何か
活性化関数とはニューラルネットワークにおいて入力から出力を決定するための関数のことです。機械学習を理解するうえで活性化関数の知識は必須項目だと思います。この記事では代表的な活性化関数の性質の説明と可視化に取り組みます。
線形パーセプトロン
単体のニューロン(神経細胞)をモデル化したものをパーセプトロンと言います。特に、単純に入力の線形結合を出力として返すようなものを線形パーセプトロンと呼ぶことがあります。入力数$N$、入力ベクトル$x_i$、シナプスにかかる重みがそれぞれ$w_i$であるような線形パーセプトロンは出力を$u$とすれば、
$$
u = \sum_{i=1}^N w_i x_i
$$
となります。適当な閾値を定めてあげれば、入力が2のパーセプトロンでAND回路を作ることもできます。以下はAND回路を再現する線形パーセプトロンを可視化するコードです。
import numpy as np
import matplotlib.pyplot as plt
def perceptron(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.8
return 1 if x1 * w1 + x2 * w2 > theta else 0
def fillcolor(val):
return "salmon" if val > 0 else "skyblue"
def plot_perceptron(func):
XX, YY = np.meshgrid(
np.linspace(-0.25, 1.25, 200),
np.linspace(-0.25, 1.25, 200)
)
XX, YY = XX.flatten(), YY.flatten()
results = [func(x, y) for x, y in zip(XX, YY)]
colors = [fillcolor(r) for r in results]
plt.figure(figsize=(6, 6))
plt.scatter(XX, YY, c=colors, s=10)
plt.xlim(-0.25, 1.25)
plt.ylim(-0.25, 1.25)
plt.xlabel("X1")
plt.ylabel("X2")
plt.text(0.5, -0.4, "Perceptron Visualization",ha="center", va="top")
plt.show()
plot_perceptron(perceptron)
結果は、
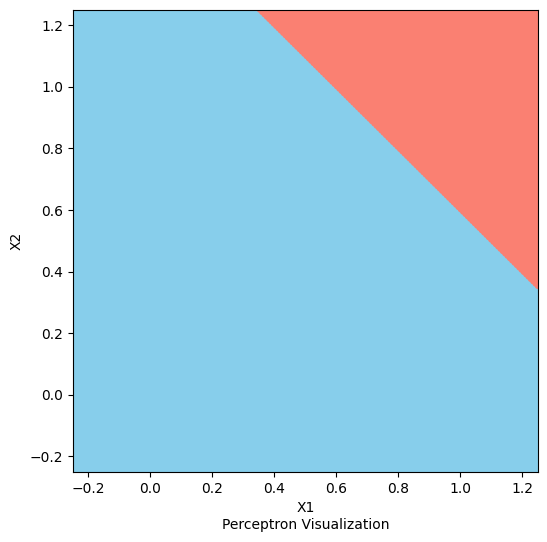
となります。青い領域を出力0、赤い領域を出力1だと思ってみるとこれがAND回路であること分かると思います。この方法で重みを変えればor回路も作ることができます。気になった方はぜひトライしてみてください。
より複雑な非線形のモデルでは出力を$y$として
$$
y=\varphi \left( \sum_{i=1}^N w_i x_i + b\right)
$$
における$\varphi$を弄っていきます。以降の活性化関数はここでの$\varphi$のことだと思って読んでください。
複雑なニューラルネットワークは活性化関数でできた巨大な合成関数です。これは厳密な表現ではありませんが、線形な関数の合成関数はまた線形です。したがって、ニューラルネットワークの複雑性のためには活性化関数は計算が容易であることと非線形であることが求められます。
シグモイド関数(Sigmoid function)
最も古典的な活性化関数にシグモイド関数があります。シグモイド関数は
$$
f(x)=\frac{1}{1+e^{-x}}
$$
です。Pythonでこの式を定義すると、
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
となります。これをmatplotlib.pyplotを使って可視化するには次のように書きます。
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10, 500)
plt.plot(x, sigmoid(x))
plt.legend(["sigmoid"], loc = "best")
plt.yticks(np.arange(0, 2, step = 0.5))
plt.xlabel("x")
plt.ylabel("y")
plt.show()
結果はこのようになります。
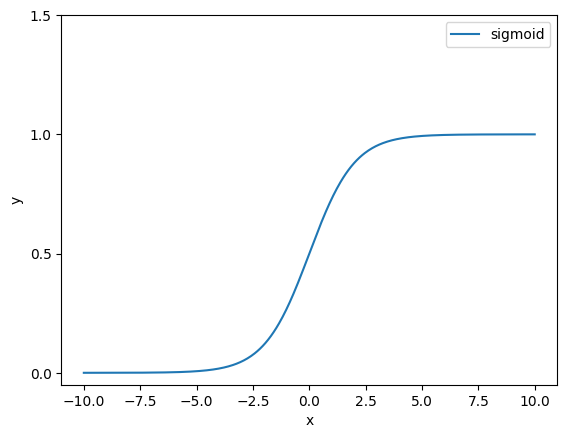
$x \to \infty $で$y = 1$、$x \to -\infty $では$y = 0$となる様子が分かります。
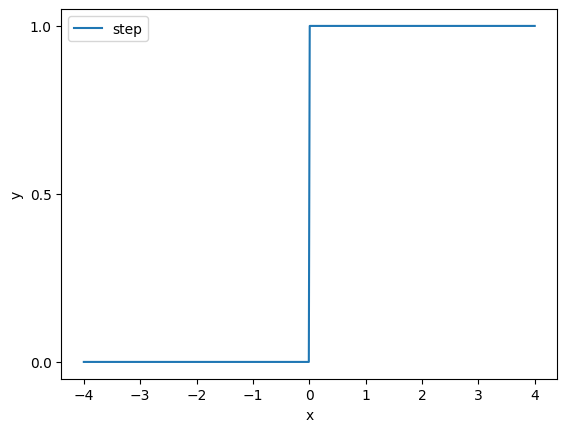
ステップ関数(Step function)
ステップ関数は非連続な関数です。機械学習でステップ関数と言えば、
$$
f(x) = \begin{cases}
1 & (x \geq 0) \\
0 & (x < 0)
\end{cases}
$$
を意味します。Pythonでこの式を定義すると、
import numpy as np
def step_func(x):
return np.where(x >= 0, 1, 0)
となります。これをmatplotlib.pyplotを使って可視化するには次のように書きます。
import numpy as np
import matplotlib.pyplot as plt
def step_func(x):
return np.where(x >= 0, 1, 0)
x = np.linspace(-4, 4, 500)
plt.plot(x, step_func(x))
plt.legend(["step"], loc = "best")
plt.yticks(np.arange(0, 1.2, step = 0.5))
plt.xlabel("x")
plt.ylabel("y")
plt.show()
双曲線正接関数(tanh fanction)
双曲線正接関数(tanh fanction)も代表的な活性化関数の一つです。定義は、
$$
f(x) = \tanh{x} =\frac{e^x-e^{-x}}{e^x+e^{-x}}
$$
です。Pythonでこの式を定義すると、
import numpy as np
def tanh(x):
return np.tanh(x)
となります。幸いにも双曲線正接関数はNumPyに含まれています。これをmatplotlib.pyplotを使って可視化するには次のように書きます。
import numpy as np
import matplotlib.pyplot as plt
def tanh(x):
return np.tanh(x)
x = np.linspace(-10, 10, 500)
plt.plot(x, tanh(x))
plt.legend(["tanh"], loc = "best")
plt.yticks(np.arange(-1.5, 2, step = 0.5))
plt.xlabel("x")
plt.ylabel("y")
plt.show()
結果は、
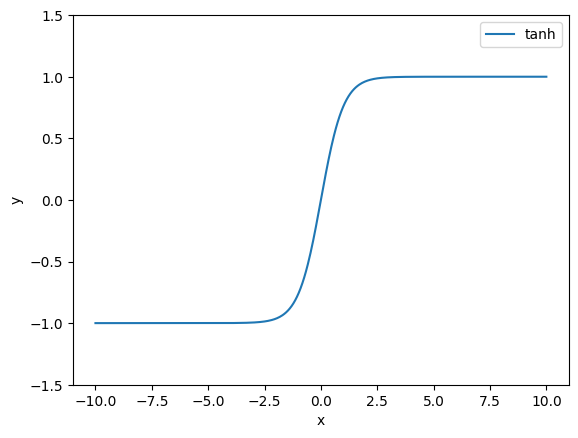
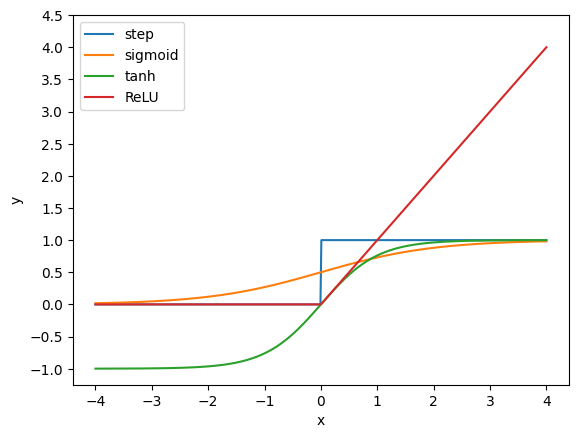
となります。形はシグモイド関数に似ていますが、$x \to \infty $で$y = 1$、$x \to -\infty $では$y = -1$となります。0近傍での傾きがシグモイド関数より大きいというのも相違点です。
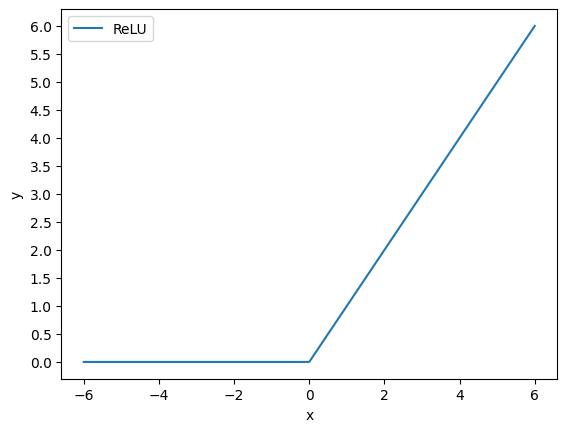
ReLU関数(ReLU function)
ReLU関数は非線形かつ計算コストが低いという、これまであげた活性化関数のいわばいいとこ取りをしたような関数で、比較的モダンな活性化関数です。定義は決して複雑でなく、
$$
f(x) =
\begin{cases}
x & (x \geq 0) \\
0 & (x < 0)
\end{cases}
$$
です。この定義は、入力$x$と定数$0$の大きいほうを出力として返す関数と言い換えることができます。したがって、Pythonでこの式を定義すると、
import numpy as np
def relu_func(x):
return np.maximum(0, x)
となります。これをmatplotlib.pyplotを使って可視化するには次のように書きます。
import numpy as np
import matplotlib.pyplot as plt
def relu_func(x):
return np.maximum(0, x)
x = np.linspace(-6, 6, 500)
plt.plot(x, relu_func(x))
plt.legend(["ReLU"], loc = "best")
plt.yticks(np.arange(0, 6.5, step = 0.5))
plt.xlabel("x")
plt.ylabel("y")
plt.show()
まとめ
これまでの活性化関数すべて同時に可視化してみましょう。これまでのコードを組み合わせて、
import numpy as np
import matplotlib.pyplot as plt
# ステップ関数
def step_func(x):
return np.where(x > 0, 1, 0)
# シグモイド関数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# tanh関数
def tanh(x):
return np.tanh(x)
# ReLU関数
def relu_func(x):
return np.maximum(0, x)
x = np.linspace(-4, 4, 500)
plt.plot(x, step_func(x))
plt.plot(x, sigmoid(x))
plt.plot(x, tanh(x))
plt.plot(x, relu_func(x))
plt.legend(["step", "sigmoid", "tanh", "ReLU"], loc = "best")
plt.yticks(np.arange(-1, 5, step = 0.5))
plt.xlabel("x")
plt.ylabel("y")
plt.show()