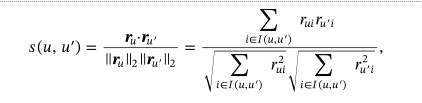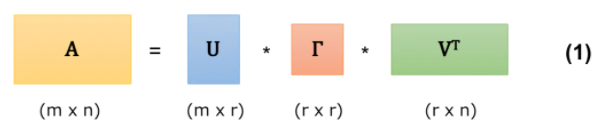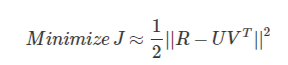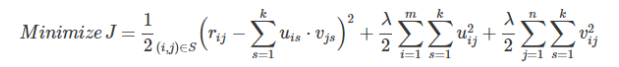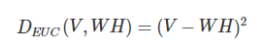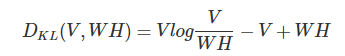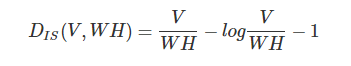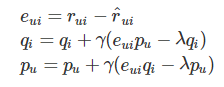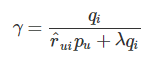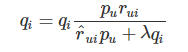【推薦システム】レコメンドアルゴリズムまとめ①【入門/協調フィルタリング/NMF】

協調フィルタリング

• 一言で表すと、ユーザーの行動履歴に基づいた推薦アルゴリズム。
• メモリベースの手法とモデルベースの手法の二種類があります。

メモリベース手法

ユーザ間の類似性やアイテム間の類似性に着目して推薦を生成する手法です。
このうち、さらにユーザーベースの手法とアイテムベースの手法に分類されます。

特徴

• ドメイン知識を必要としない(商品の内容を知らなくてもレコメンドできる)
• 異なるジャンルをまたいだ推薦ができる
• 利用者が多い場合に有利
• 推定の都度全データに対して計算を行う(類似度を計算する)アプローチをとるのでデータのサイズに比例して計算コストが高くなる。

ユーザーベース

対象となるユーザーと類似した嗜好を持つユーザーのグループを調べることによって、各ユーザーに適したレコメンデーションを提供する手法です。

• メリット

  • アルゴリズムがシンプル、データセットが頻繁に変更されても対応できる。

• デメリット

  • 巨大なデータセットを用いると時間がかかる。ユーザ（製品）が増えるほど時間がかかる。

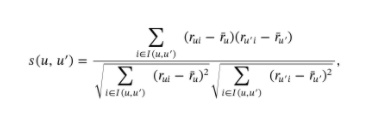
(補足)代表的なユーザーの類似度を評価する方法

• ピアソン相関係数

いわゆる相関係数というやつ。ユーザー同士の線形な関係が強いほど大きな値をとり、ユーザー同士の類似度を図ることができる。

• コサイン類似度

ユーザー同士の評価ベクトル r (あるユーザーのそれぞれのアイテムに対する評価値を表現したベクトル)の類似度をベクトルのなす角の余弦の値によって評価する。

• その他
  • 強制ピアソン相関係数
  • スピアマン相関係数
  • ケンドールのτ相関係数
  • 調整済みコサイン類似度

アイテムベース

あるユーザーのアイテムに対する評価値をそのアイテムと似ているアイテムに付けられた評価値を利用して予測する手法です。Amazonで採用されているらしい。
類似度の計算をオフラインで行うことでスケーラビリティを確保している。

• メリット

  • 疎なデータセットに対して性能が優れている（高速）。
  • 事前に共起情報をチェックすることで計算時間を短縮することが可能

• デメリット

  • アイテムの類似度のディクショナリの管理をする必要がある。
  • すべてのユーザーに同じ商品が推薦される。

推薦手順

1. ユーザーの嗜好データを取得する(ユーザー×アイテム行列)
2. 1で得た嗜好データに基づいてユーザー間の類似度を計算
3. ターゲットのユーザーに対して似ているユーザーを抽出
4. 似ているユーザーが購入している商品をレコメンド

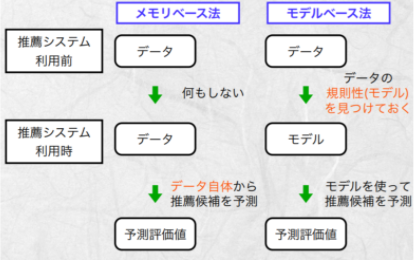
モデルベース手法

決定木、ルールベース推論、ナイーブベイズ分類器、行列因数分解技術などの機械学習やデータマイニング技術を用いて、対象となるユーザーに適したアイテムを予測する手法です。メモリベース手法が蓄積したデータを推薦時に直接用いて予測するのに対して事前に調べておいたデータの規則性(モデル)を使って予測します。

Cold Start問題

とは？

協調フィルタリング手法ではメモリベースでは特に、ユーザーとアイテムの嗜好に関するデータがある程度集まらないと有意な推薦ができないという問題が生じます。ユーザーがアイテムを評価しないと協調フィルタリングでは新しいユーザーにアイテムを推薦したり新しいアイテムをユーザーに推薦することができません。

対処方法

• 新規ユーザーに対して

  • 新規ユーザーの属性(性別や年齢などの特徴)を用いて似ているユーザーが過去に高い評価を与えたアイテムをおすすめする。

• 新規アイテムに関して

  • 新規アイテムの属性(カテゴリや値段などの特徴)を用いて似ているアイテムに高い評価を与えたユーザーに新規アイテムをおすすめする方法。

• その他参考事例

  • LINE( https://logmi.jp/tech/articles/322247)
  • バンディットアルゴリズムとよばれる手法を用いてユーザーの行動ログ・行動パターンが不足している新しいアイテムの推薦にデータを取得して予測精度を上げることと一番良いアイテムを選ぶことの2つを同時に行うとで高性能な推薦を実現してる様子

特異値分解(SVD)

とは？

• スパースな行列を密な表現に変換する次元削減手法の一つ。
• 以下のように m × n の行列 A を三つのベクトルに分解します。
  

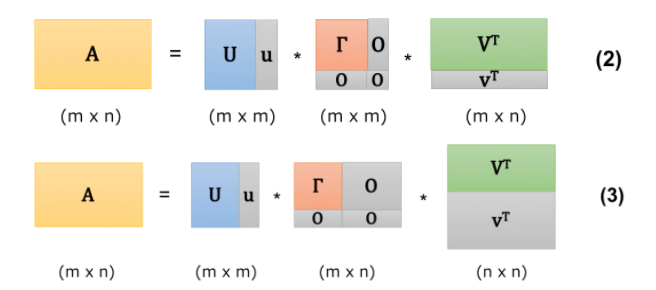
詳細に書くと以下のようになります。(以下では次元数は r ⇒nとなっている)

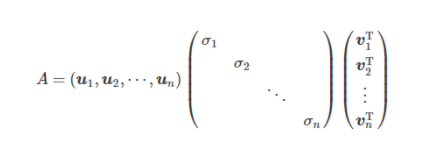
ここでU、Vはそれぞれ直交行列(転置行列がそのまま逆行列になるような行列)であり、Γは対角成分上に上か降順で特異値と呼ばれる値が並んでいる正方行列です。

• U,Vの列ベクトルをそれぞれ左特異ベクトル、右特異ベクトルと呼ぶ。
• 行列Aの特異値の二乗 = 行列AAT 、ATAの固有値が成立
• 分解の方法には一般に以下の二つがある
  

(2)の表記では 0 を特異値に入れてΓをm×mの形に成型し,0の特異値の分の得意ベクトルをそれぞれU,Vに追加している。
(3)でも同様に０を特異値に入れるがこちらではΓをm × n に成型しています。追加した０の特異値の分の特異ベクトルをそれぞれU、Vに追加しています。
(2),(3)いずれもグレーの部分はかけ合わせて0 になるのでΓの成型方法の選択による実質的な影響はありません。

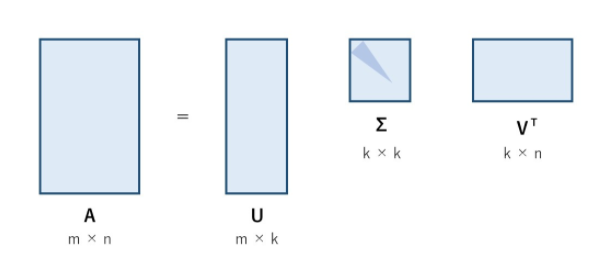
どう使うのか?

• 降順に並んでいる特異値のうち、任意の上位n個だけについて行列積を計算する
  

上の画像であれば、k個の特異値のうち上から l 個(上図の濃い青)についてだけ考えると U はm × l 、Vはk ×n の重要な部分(特異値が大きい部分)だけを取り出して考えることができる。(ここで l < k)

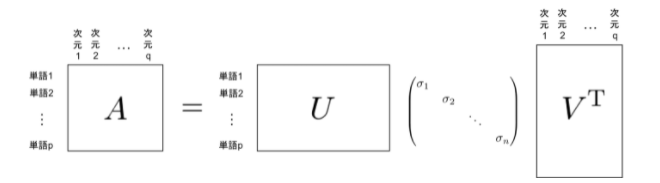
• 具体的に自然言語処理で単語の分散表現を扱う例を考えると、分散表現Aにたいして特異値分解を用いると以下のように三つの行列に分解できます。

ここで次元数を見てみると最終的に出てくる単語の表現ベクトルはUの各行ベクトルであることがわかります(行数が単語数に相当しているため)。ここで特異値σについて、上から任意のk ( < n)個だけを見てやると、行列 U の行ベクトルは以下のようにより小さい次元に圧縮できることがわかります(図の赤い部分)

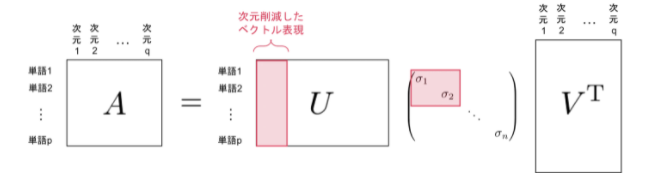
このようにして、特異値分解を用いてより密な分散表現を得ることができました。

固有値分解との違い

• 固有値分解(A = PDPt、Dは固有値を対角成分に持つ対角行列、大学のテストとかでAnを求めさせる問題でよく出るやつ)は正方行列にしか使えないが、特異値分解は長方行列にも可能。

Matrix Factorization

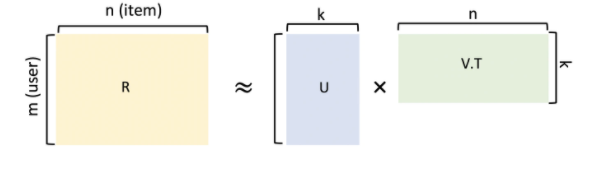
• SVD同様、ユーザー×アイテム行列の次元削減のために取られる手法。
• ユーザーアイテム行列R (m×n)が R ≒ UVTのように二つの行列の積に近似することを考えます。(ここで一見U,Vがそれぞれユーザー、アイテムのそれぞれの相関を表しているように思えますが、U,Vの各要素は単なる潜在因子なので必ずしも解釈可能だとは限りません。)

ここで考えたいのは当然近似した二つの行列積とRそのものの誤差を小さくするために損失関数を考えます。ここでは行列同士の距離としてユークリッド距離を採用します。

実際のデータには欠損値が数多く含まれているため、このままではうまく最適化できないため、実際に観測されたユーザーアイテムペア(i, j)∈Sの評価値 ri,jを用いて書き直します。

右辺の後半二項は正則化項です。

• 重みの更新自体はSGD,ALSを用いて更新することが多い。

NMF(Nonnegative Matrix Factorization)

• Matrix Factorizationのうちで、元行列Vと分解したW,Hの要素の値がすべて非負値であるものの行列分解を指してNonnegative Matrix Factorizationと呼んでいる(?)。

• レコメンドで用いるユーザーによるアイテムの評価値は非負で表すことが一般的であり、また基底ベクトルと係数を非負に限定することで、係数が疎になりやすくなって理解しやすくなるらしい。

• NMFで用いる行列間の距離いろいろ

  • ユークリッド距離
    
  • カルバック・ライブラー距離(KLダイバージェンス)

  

  • Itakura-Saito距離（IS）
    

• どのようにして非負の値に分解していくのか

  • 「最初の値がすべて非負」と「更新式に引き算がない」という条件を満たせば原理的にすべての要素が非負の行列に分解できる。
  • ruiをユーザーuによるアイテムi の評価値,、p,qをそれぞれ分解した行列P,Qの各要素だとすると更新式は以下のようになります。

  

更新式から引き算を消すために真ん中の式から学習率を以下のように表して

代入すると以下のように、引き算の無い形で更新をおこなうことが出来、非負の行列に変換することができます。