1. はじめに
この記事は、ゼロから作るDeep Learning④強化学習編の備忘録です。詳細なコードは、書籍のサンプルコードを参照ください。
本記事では、強化学習の状態空間と行動空間に関するテーブル形式の解法について説明します。関数近似による解法は別の記事で説明する予定です。
2. マルコフ決定過程
マルコフ決定過程(Markov Decision Process: MDP)について説明します。
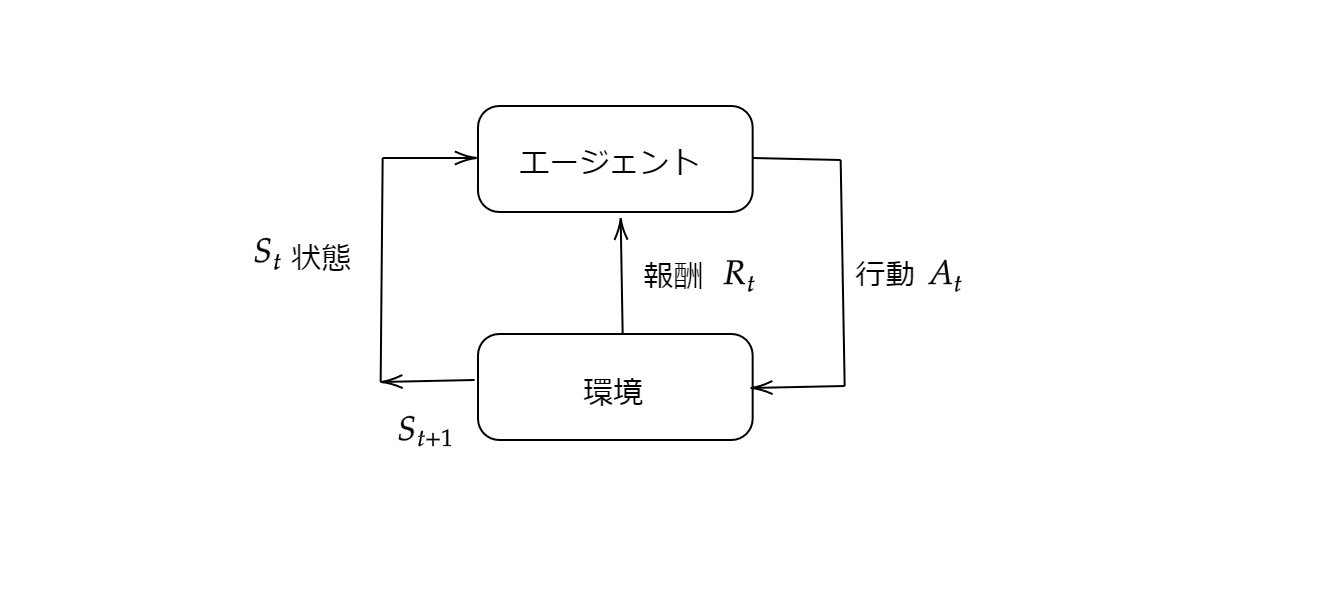
マルコフ決定過程を導入することで、強化学習問題を正確な理論的記述が可能となります。意思決定者はエージェントと呼ばれ、エージェントと相互作用するものは環境と呼びます。エージェントが状態$S_t$で行動$A_t$することで、環境から報酬$R_t$と次の状態$S_{t+1}$について教えてもらいます。
マルコフ決定過程とエージェントは、ともに次のように始まる系列を生成します。
S_0, A_0, R_1, S_1, A_1, R_2 \cdots
このときの状態遷移確率は$p(s^\prime|s,a)$であり、報酬関数は$r(s,a,s^\prime)$であり、エージェントの方策は$\pi(a|s)$です。
エージェントの目標は獲得する報酬の総和である収益$G_t$を最大化することです。
G_t = R_{t+1}+R_{t+2}+R_{t+2}+\cdots
終端の時刻が長い連続タスクでは、簡単に収益$G_t$が無限大になってしまいます。そこで、割引率$\gamma$を導入した割引収益を最大化することを考えることにします。
G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+2}+\cdots
割引収益は式変形をすれば以下を得ることができます。
G_t = R_{t+1}+\gamma G_{t+1}
割引収益$G_t$を最大にすることが、エージェントの目標です。しかしながら、確率的に行動し状態遷移するので、収益を決定論的に最大化するのは不適切です。そのため、収益の期待値として状態価値関数$v_\pi(s)$を定義します。
v_\pi(s)=\mathbb{E}[G_t|S_t=s,\pi]=\mathbb{E}_\pi[G_t|S_t=s] \tag{1}
状態価値関数$v_\pi(s)$を最大化するように、エージェントは行動$a$を選択すればよいことがわかります。
状態価値関数に行動$a$の条件を付加したのが行動価値関数$q_\pi(s,a)$です。
q_\pi(s)=\mathbb{E}[G_t|S_t=s,A_t=a,\pi]=\mathbb{E}_\pi[G_t|S_t=s,A_t=a] \tag{2}
3. ベルマン方程式
3.1 ベルマン方程式
ベルマン方程式について説明します。
ベルマン方程式より、状態価値関数$v_\pi(s)$と行動価値関数$q_\pi(s,a)$が与えられます。
v_\pi(s)=\sum_a\sum_{s^\prime}\pi(a|s)p(s^\prime|s,a)\lbrace r(s,a,s^\prime)+\gamma v_\pi(s^\prime)\rbrace \tag{3}
q_\pi(s,a)=\sum_{s^\prime}p(s^\prime|s,a)
\lbrace r(s,a,s^\prime)+\gamma v_\pi(s^\prime)\rbrace\tag{4}
状態価値関数$v_\pi(s)$の導出についてみていきましょう。
\begin{eqnarray}
v_\pi(s)
&=&\mathbb{E}_\pi[G_t|S_t=s]\\
&=&\mathbb{E}_\pi[R_t+\gamma G_{t+1}|S_t=s]\\
&=&\sum_a\sum_{s^\prime}\pi(a|s)p(s^\prime|s,a)\lbrace r(s,a,s^\prime)+\gamma v_\pi(s^\prime)\rbrace
\end{eqnarray}
最後の等式、少しはしょってますよね。以下の関係を用いました。
\begin{eqnarray}
\mathbb{E}_\pi[G_{t+1}|S_t=s]
&=&\sum_a\sum_{s^\prime}\pi(a|s)p(s^\prime|s,a)\mathbb{E}_\pi[G_{t+1}|S_{t+1}=s^\prime]\\
&=&\sum_a\sum_{s^\prime}\pi(a|s)p(s^\prime|s,a)v_{\pi}(s^\prime)
\end{eqnarray}
式(3)の状態価値関数$v_\pi(s)$の意味についてみていきましょう。
状態$s$が与えられたとき、$a$と$s^\prime$が同時に起こる確率$\pi(a|s)p(s^\prime|s,a)$と、現時刻の報酬$r(s,a,s^\prime)$と$\gamma\in(0,1)$で割り引いた将来の状態価値関数$v_\pi(s^\prime)$の期待値です。
式(4)の行動価値関数$q_\pi(s)$の意味についてみていきましょう。
状態$s$と行動$a$が与えられたとき、$s^\prime$が起こる確率$p(s^\prime|s,a)$と、現時刻の報酬$r(s,a,s^\prime)$と$\gamma\in(0,1)$で割り引いた将来の状態価値関数$v_\pi(s^\prime)$の期待値です。
状態価値関数と行動価値関数には以下の関係があります。式(5)に式(4)を代入すれば、式(3)が得られることからも確認できます。
v_\pi(s) = \sum_{a}\pi(a|s)q_\pi(s,a) \tag{5}
3.2 ベルマン最適方程式
最適方策がわかったときのベルマン方程式について説明します。
最適方策は、式(5)を眺めてみれば、行動価値関数$q_\pi(s,a)$が最大となる行動$a$を100%の確率で選択すれば、状態価値関数$v_\pi(s)$を最大化できることがわかります。式(6)をベルマン最適方程式といいます。
v_\ast(s) = \max_{a}q_{\ast}(s,a) \tag{6}
ただし、方策が決定論的に定まるので、行動価値関数$q_\pi(s,a)$と状態価値関数$v_\pi(s)$は、行動価値関数$q_\ast(s,a)$と状態価値関数$v_\ast(s)$と表記してます。
行動価値関数を最大化することを考えることは、状態価値関数を最大化するように行動$a$を選択すれば、行動価値関数の最適値は状態価値関数の最適値と一致することがわかります。
最適行動価値関数(Optimal Action-Value Function)はどうなるでしょう。式(6)を式(4)に代入すれば求まります。
q_{\ast}(s,a)=\sum_{s^\prime}p(s^\prime|s,a)
\lbrace r(s,a,s^\prime)+\gamma v_\ast(s^\prime)\rbrace\tag{7}
最適方策$\mu_{\ast}(s)$は、以下の式で得られます。
\mu_{\ast}(s) = \underset{a} {\operatorname{argmax}} q_\ast(s,a) \tag{8}
4. 動的計画法
最適方策を直接得ることは難しいです。最適方策を推定する方法として、方策反復法や価値反復法があります。
4.1 方策反復法
方策$\pi(a|s)$と状態価値関数$V_\pi(s)$を交互に更新することで、最適方策$\mu_\ast(s)$とベルマン最適方程式$V_\ast(s)$を求めます。
- step 1. 初期化
方策$\pi(a|s)$に適当な確率を割り当てます。
0,1,2,3が行為であり、割り当てられた各確率は1/4です。
pi[state]={0:1/4, 1:1/4, 2:1/4, 3:1/4}
- step 2. 方策評価
状態価値関数$V_\pi(s)$を更新します。
方策$\pi(a|s)$に基づいて、状態価値観数$V_\pi(s)$が求まります。
更新前と更新後の$V_\pi(s)$の差が$\epsilon$未満になるまでstep2を実行。
while True:
old_V = V
new_V = 0
th = 1e-3
for state in states:
for action,action_prob in pi[state].items():
next_state = f(state,action)
r = reward(state,action,next_state)
new_V += action_prob*(r+gamma*V[next_state])
V[state] = new_V
delta = 0
for state in states:
t = abs(V[state]-old_V[state])
if delta<t:
delta = t
if delta < th:
break
- step 3. 方策改善
方策$\pi(a|s)$を更新します。
いまある状態価値観数$V_\pi(s)$に基づいて、各状態$s$における最適方策を求めます。
更新前と更新後の方策が一致していれば、これ以上方策を改善できないので計算終了。
while True:
old_pi = pi
for state in states:
Q = {}
for action in actions:
next_state = f(state,action)
r = reawrd(state,action,next_state)
Q[action] = r+gamma*V[next_state]
max_action = argmax(Q)
pi[state] = {0:0, 1:0, 2:0, 3:0}
pi[state][max_action] = 1
- step 4. step 2.に戻ります。
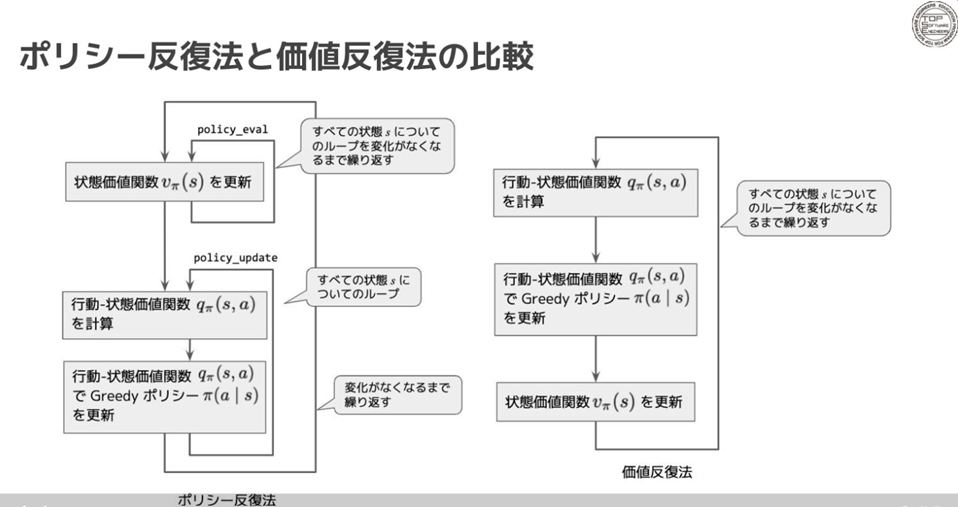
4.2 価値反復法
方策反復法は方策評価のステップが終了するまで方策は固定です。一方で、状態価値関数を更新する度に逐次的に方策を更新するアルゴリズムが価値反復法になります。
5. MC法
前章のアルゴリズムでは、次の状態や報酬が決定論的にわかっていました。これは、環境のモデルが既知であることを想定しています。確率的にしか次の状態や報酬がわからない環境では、前章の方策反復法は適用できないです。
next_state = f(state,action)
r = reawrd(state,action,next_state)
次の状態や報酬が確率的にしかわからない環境でも、強化学習を適用できるようにするために、モンテカルロ法(MC法)を新たに導入します。モンテカルロ法は、データから期待値を直接推定することが出来ます。そのため、前章の方策評価のところで、状態価値関数$V_\pi(s)$および行動価値関数$Q_\pi(s,a)$を、モンテカルロ法を用いて直接推定すれば、確率的にしか次の状態や報酬がわからない環境でも、方策反復法を適用することが出来るようになります。
6. TD法
TD法は、動的計画法とMC法のアイディアを組み合わせたもので、強化学習の中でも斬新なアイデアのひとつです。
6.1 TD法とMC法の比較
時間的差分学習法(Temporal Difference法:TD法)は、MC法を改善した手法です。
MC法は、収益$G_t$の加重平均で状態価値関数$V_\pi(S_t)$を更新します。
V_\pi^\prime(S_t)\leftarrow V_\pi(S_t)+\alpha (\color{red}{G_t}-V_\pi(S_t))
TD法は、収益$G_t$の推定値$R_t+\gamma V_\pi(S_{t+1})$の加重平均で状態価値関数$V_\pi(S_t)$を更新します。
V_\pi^\prime(S_t)\leftarrow V_\pi(S_t)+\alpha (\color{red}{R_t+\gamma V_\pi(S_{t+1})}-V_\pi(S_t))
-
MC法では、収益$G_t$を用いる必要があり、ゴールの最後まで計算する必要がありました。しかし、TD法では、ブーストラップ(推測から推測すること)を導入することで、動的計画法のように価値関数を逐次更新できるようになり、より速く学習が進められるようになりました。
-
MC法と同じく、次の状態や報酬に関する環境モデルを使用せず、サンプリングしたデータから価値関数を更新することが出来ます。
6.2 SARSAとQ学習
前節で紹介した状態化値関数$V_{\pi}(S_t)$を行動価値関数$Q_{\pi}(S_t,A_t)$に置き換えたアルゴリズムとして、SARSAとQ学習があります。
SARSAは、ベルマン方程式に着目して行動価値関数の更新式を設計してます。
Q_\pi^\prime(S_t,A_t)\leftarrow Q_\pi(S_t,A_t)+\alpha (\color{red}{R_t+\gamma Q_\pi(S_{t+1},A_{t+1})}-Q_\pi(S_t,A_t))
Q学習は、ベルマン最適方程式に着目して行動価値関数の更新式を設計してます。
Q_\pi^\prime(S_t,A_t)\leftarrow Q_\pi(S_t,A_t)+\alpha (\color{red}{R_t+\gamma \max_{a}Q_\pi(S_{t+1},A_{t+1}=a)}-Q_\pi(S_t,A_t))
6.3 DQN
Q学習は、ベルマン最適方程式に着目して行動価値関数の更新式が設計されていました。
Q_\pi^\prime(S_t,A_t)\leftarrow Q_\pi(S_t,A_t)+\alpha (\color{red}{R_t+\gamma \max_{a}Q_\pi(S_{t+1},A_{t+1}=a)}-Q_\pi(S_t,A_t))
それでは、DQNのメインアイディアを紹介します。
まず、パラメータ$\theta$を固定して、最適方策$A_t$を行動価値関数$Q_{\hat{\theta}}(S_t,A_t)$から選択します。最適方策$A_t$に基づいて行動し、環境から次の状態$S_{t+1}$を観測します。
行動価値関数$Q_{\theta}(S_t,A_t)$のパラメータ$\theta$を探索します。どうすればよいでしょうか?
ターゲットを$R_t+\gamma \max_{a}Q_{\hat{\theta}}(S_{t+1},A_{t+1})$とします。ターゲットに対して、行動価値関数のニューラルネットワーク$Q_{\theta}(S_t,A_t)$との誤差が最小になるようにニューラルネットワークのパラメータ$\theta$を更新すればよさそうです。
\theta \leftarrow \arg \min_{\theta} \|R_t+\gamma \max_{a}Q_{\hat{\theta}}(S_{t+1},A_{t+1}=a)- Q_{\theta}(S_t,A_t)\|
他にも、経験再生など多くの工夫を組み込むことで、飛躍的に性能が向上しました。
7. おわりに
方策反復法がなぜ最適解に収束するのかはわからなかったです。
おすすめの文献があればご教示頂ければ幸いです。
これがおすすめらしい。
8. 参考文献
- ゼロから作るDeep Learning④ 強化学習編、斎藤 康毅
- Reinforcement Learning: An Introduction Second Edition、Richard S. Sutton、Andrew G. Barto