前回の復習
1.2.4 ガウス分布
ガウス分布(正規分布)とは
- 連続変数の確率分布の中の一種類
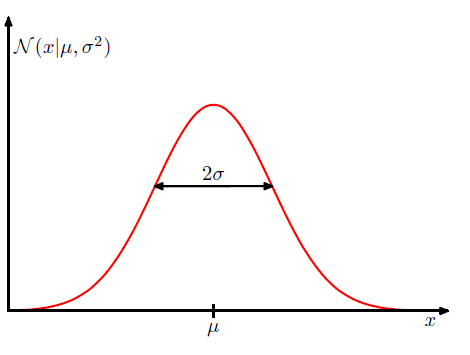
- 平均付近が一番高く、平均から離れるにつれて緩やかに低くなっていく、左右対称な釣り鐘型の分布(下図参照)
変数$x$に対し、ガウス分布を式で表すと以下のようになる
\mathcal{N}(x |\mu,\sigma^2)=\frac{1}{(2\pi\sigma^2)^{1/2}}\exp\biggl\{-\frac{1}{2\sigma}(x-\mu)^2\biggr\}
$\mu$・・・平均
$\sigma^2$・・・分散
$\sigma$・・・標準偏差
$\beta=1/\sigma^2$・・・精度パラメータ
図示すると
以下の条件を満たす
\mathcal{N}(x |\mu,\sigma^2)>0
図からも分かるし変数$x$が指数であることから分かる
\int_{-\infty}^{\infty}\mathcal{N}(x |\mu,\sigma^2)=1
ガウス積分の公式をつかって計算すればできる
http://mathtrain.jp/gauss
詳しい計算は割愛
→確率密度の条件を満たしている
ガウス分布の期待値(平均値)
期待値の定義より
\boldsymbol{E}[x]=\int_{-\infty}^{\infty}\mathcal{N}(x |\mu,\sigma^2)x\mathrm{d}x=\mu\ \ \ \ \ \ \ \ \ ①
詳しい計算は割愛(http://mathtrain.jp/gaussdistribution)
ガウス分布の分散
先週やった分散の定義より
var[x]=\boldsymbol{E}[x^2]-\boldsymbol{E}[x]^2
$\boldsymbol{E}[x]^2$は①を2乗すれば求められる
$\boldsymbol{E}[x^2]$を求めたい
\boldsymbol{E}[x]=\int_{-\infty}^{\infty}\mathcal{N}(x |\mu,\sigma^2)x^2\mathrm{d}x=\mu^2+\sigma^2\ \ \ \ \ \ \ \ ②
詳しい計算は割愛(http://mathtrain.jp/gaussdistribution)
①と②より
var[x]=\boldsymbol{E}[x^2]-\boldsymbol{E}[x]^2=\sigma^2
また、分布の最大値を与える$x$はモード(最頻値=一番よく出る値みたいな)と呼ばれ、ガウス分布においてはピークの$x$がそれになる。
ここまでのまとめ
- ガウス分布は左右対称な釣り鐘型の分布
\mathcal{N}(x |\mu,\sigma^2)=\frac{1}{(2\pi\sigma^2)^{1/2}}\exp\biggl\{-\frac{1}{2\sigma}(x-\mu)^2\biggr\}
- ガウス分布の分散はその期待値によって、
var[x]=\boldsymbol{E}[x^2]-\boldsymbol{E}[x]^2=\sigma^2
で表される
補足
p25見てると確率分布と確率密度がごっちゃになってきた
確率密度関数
\mathcal{N}(x |\mu,\sigma^2)=\frac{1}{(2\pi\sigma^2)^{1/2}}\exp\biggl\{-\frac{1}{2\sigma}(x-\mu)^2\biggr\}
を満たす確率分布がガウス分布
確率分布関数と確率密度関数
http://www.na.scitec.kobe-u.ac.jp/~yamamoto/lectures/computationalfinance/chapter3.PDF
ここで言ってる確率分布関数はPRMLの累積分布関数のようにみえっる
D次元ベクトルの連続変数xに対して定義されるガウス分布
D次元ベクトルの連続変数は以下の式で与えられる
\mathcal{N}(\mathrm{x} |\boldsymbol{\mu},\boldsymbol{\Sigma})=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\boldsymbol{\Sigma}|^{1/2}
}\exp\biggl\{-\frac{1}{2\sigma}(x-\mu)^2\biggr\}
ここに2次元での例で説明は載っている
http://mathtrain.jp/tahenryogauss
- 全空間で積分すると1になること
- 期待値が μ であること
- 分散共分散行列が Σ であること
2.3節でやるとのことなので、ここでの説明は割愛
xがデータ集合の場合
次はデータ集合$\boldsymbol{x}$の場合を考える。
一番最初に説明した$x$は単一の観測における$x$。今回は複数観測した場合において考えてみる
\boldsymbol{x}=(x_1,x_2,x_3,......,x_N)^T
データ店が同じ分布から独立に生成されるとき、独立同分布(i.i.d.)という。
今回の$\boldsymbol{x}$もその条件を満たす
- 同じ分布(ガウス分布)から生成されている
- それぞれ($x_1,x_2,...,x_N$)は独立。(ある一つの結果がほかの結果に影響しない)
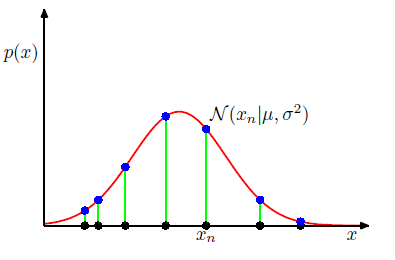
以上よりデータ集合の確率は以下の式で表される
p(\boldsymbol{x}|\mu,\sigma^2)=\prod_{n=1}^{N}\mathcal{N}(x_n|\mu,\sigma^2)
尤度関数については前回やりました(http://mathtrain.jp/mle)
ここから尤もらしいp(一番確かだろうと思われるp)を考えることで、$\mu$と$\sigma^2$をきめて確率分布の形を導き出したい(とんがってるのか、そうでないのか、ピークがどこにあるのかなど。)
μとσ^2を求めていく
尤度関数を対数化して最大化することで値を決める。最尤法
→尤度関数を単調増加関数である対数にして、最大化(微分して傾きが0になる部分(ピーク)を求める)することで値を決める
尤度関数を対数化すると、(時間あれば計算式を)
\ln p(\boldsymbol{x}|\mu,\sigma^2)=-\frac{1}{2\sigma^2}\sum_{n-1}^{N}(x_n-\mu)^2-\frac{N}{2}ln \sigma^2-\frac{N}{2}ln (2\pi)
両辺$\mu$で微分して左辺0として最尤推定の$\mu$が得られる
\mu_{ML}=\frac{1}{N}\sum_{n=1}^{N}x_n
これは観測値の平均を意味している。
$\sigma^2$について最大化してあげると、
\sigma_{ML}^2=\frac{1}{N}\sum_{n=1}^{N}(x_n-\mu_{ML})^2
これは観測値の平均に対する観測値の分散になっていることが分かる
ここで$\mu_{ML}$、$\sigma_{ML}^2$に関しての期待値を考える。
つまり、Nをどんどん増やしていった時の平均値。
簡単な計算(http://prml.2apes.com/1-12-%E6%A8%99%E6%9C%AC%E5%88%86%E6%95%A3%E3%81%AE%E8%87%AA%E7%94%B1%E5%BA%A6/)
で以下のように求まる
\boldsymbol{E}[\mu_{ML}]=\mu
\boldsymbol{E}[\sigma_{ML}^2]=\Bigr(\frac{N-1}{N}\Bigr)\sigma^2
真の分散は$(N-1)/N$倍過小評価されることが分かる
この現象をバイアスという。
直感的にみてみると
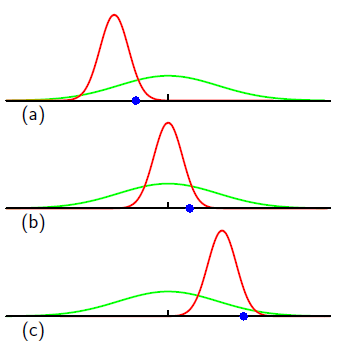
つまり、サンプル数が少なかったら確率分布の形を変に見積もっちゃうということ。
ここまでのまとめ
- データ集合$\boldsymbol{x}$に関して最尤法をつかってもっともらしい$\mu$と$\sigma^2$を求めた。
\mu_{ML}=\frac{1}{N}\sum_{n=1}^{N}x_n
\sigma_{ML}^2=\frac{1}{N}\sum_{n=1}^{N}(x_n-\mu_{ML})^2
- サンプル数が少ない場合は最尤推定は使えない
補足
① シグマは総和、パイは総乗なので注意。掛け算しまくってるやつがパイ
②データ集合の確率がピンと来ない→N回試行してそれぞれの値が$x_1$かつ$x_2$かつ$x_3$かつ$...x_N$だった時の確率
③単調増加関数などhttp://mathtrain.jp/tantyou
1.2.5曲線フィッティング再訪
1.1の復習
進む前に軽く復習
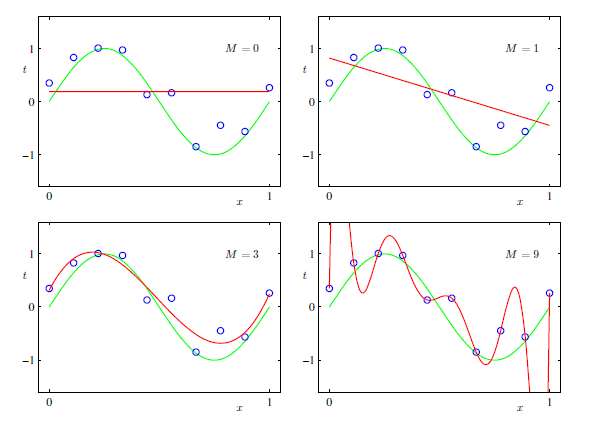

観測値に対して、多項式曲線(1.1)でフィッテングして次の値を予測した。
その際、代表的な誤差関数である二乗和誤差(1.2)が最小になるようにいろいろやった。
N個の入力値で構成される訓練データの集合$\boldsymbol{x}=(x_1,...,x_N)^T$とそれに対する目標値$\boldsymbol{t}=(t_1,...,t_N)^T$があった。上図参照
また、過学習への対策として正則化項を導入することでM=9のときもまともな形に見れることも学んだ。
1.1で行った曲線フィッティングを最尤推定で解いていく
1.1と同じようにN個の入力値で構成される訓練データの集合$\boldsymbol{x}=(x_1,...,x_N)^T$とそれに対する目標値$\boldsymbol{t}=(t_1,...,t_N)^T$を考える。
この値に基づいて新たな入力値$x$に対する目標関数$t$の予測ができるようにする。
前提として、入力値$x$に対し、対応する$t$は平均が式(1.1)で与えられる多項式曲線$y(x,\boldsymbol{w})$に等しいガウス分布に従うものとする
式で表すと
p(t|x,\boldsymbol{w},\beta)=\mathcal{N}(t|y(x,\boldsymbol{w}),\beta^{-1})
$\beta$は精度パラメータ($1/\sigma^2$)
模式的に表した図が以下の図
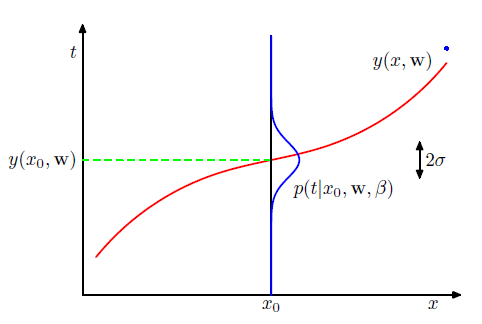
真の曲線上に並ぶはずのデータがノイズにより、ガウス分布に従って散らばっていることを表している。
ここで訓練データ{$\boldsymbol{x},\boldsymbol{t}$}を使って未知のパラメータ$\boldsymbol{w},\beta$を最尤推定で求めていく
独立同分布なので尤度関数は以下のようになる
p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)=\prod_{n=1}^{N}\mathcal{N}(t_n|y(x_n,\boldsymbol{w}),\beta^{-1})\ \ \ \ \ \ \ ①
データ集合$\boldsymbol{x}$に対して最尤推定を行った時と同様に対数を最大化(対数とって微分して)して、$\boldsymbol{w}_{ML}$、$\beta$ _MLを求める
①にガウス分布の式を代入して対数尤度関数にすると
\ln p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)=-\frac{\beta}{2}\sum_{n=1}^{N}\{y(x_n,\boldsymbol{w})-t_n\}^2+\frac{N}{2}\ln \beta-\frac{N}{2}ln (2\pi)
この式を$\boldsymbol{w}$について最大化すると、$\boldsymbol{w}_{ML}$が求まる
その時に微分をするので$\boldsymbol{w}$が含まれない項(右辺の最後の二つの項)は無視できる。
また、正の定数倍(なぜ正のみなのだろうか?)しても$\boldsymbol{w}$の最大値の位置は変わらないので、$\beta/2$を$1/2$で置き換えることができる。
対数尤度を最大化する
\frac{d}{d\boldsymbol{w}}\ln p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)=\frac{d}{d\boldsymbol{w}}\Bigr(-\frac{\beta}{2}\sum_{n=1}^{N}\{y(x_n,\boldsymbol{w})-t_n\}^2\Bigr)=0
は
二乗和誤差の最小化
-\frac{d}{d\boldsymbol{w}}\ln p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)=\frac{d}{d\boldsymbol{w}}\Bigr(\frac{1}{2}\sum_{n=1}^{N}\{y(x_n,\boldsymbol{w})-t_n\}^2\Bigr)=0
と等価
MAP推定
$w$の事後分布を最大化することで、尤もらしい$w$を導き出す。
まず、多項式の係数$w$に関する事前分布を適当にガウス分布(平均0、分散α^{-1})と仮定して導入する
p(\boldsymbol{w}|\alpha)=\mathcal{N}(\boldsymbol{w}|\boldsymbol{0},\alpha^{-1}\boldsymbol{I})=\Bigr(\frac{\alpha}{2\pi}\Bigr)^{(M+1)/2}exp\Bigr\{-\frac{\alpha}{2}\boldsymbol{w}^T\boldsymbol{w}\Bigr\}
$\alpha$は分布の精度パラメータであり、M+1はM次多項式に対する$\boldsymbol{w}$の要素数である。
$\alpha$のようにモデルパラメータの分布を制御するパラメータを超パラメータという。
$\boldsymbol{w}$の事後分布は事前分布と尤度関数との積に比例し、
p(\boldsymbol{w}|\boldsymbol{x},\boldsymbol{t},\alpha,\beta)\propto p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)p(\boldsymbol{w},\alpha)
これで与えられたデータに基づいてもっとも確からしい$\boldsymbol{w}$の値を見つける
→事後分布を最大化する$\boldsymbol{w}$を決めることができる
→このテクニックをMAP(maximum posterior)推定と呼ぶ
もろもろ組み合わせて計算して
\frac{\beta}{2}\sum_{n=1}^{N}\{y(x_n,\boldsymbol{w})-t_n\}^2+\frac{\alpha}{2}\boldsymbol{w}^T\boldsymbol{w}
ここから事後分布の最大化は二乗和誤差の最小化と等価であることが分かる。
また正則化パラメータを$\lambda=\alpha/\beta$で与えられる。
1.1で正則化項を導入した二乗和誤差と酷似
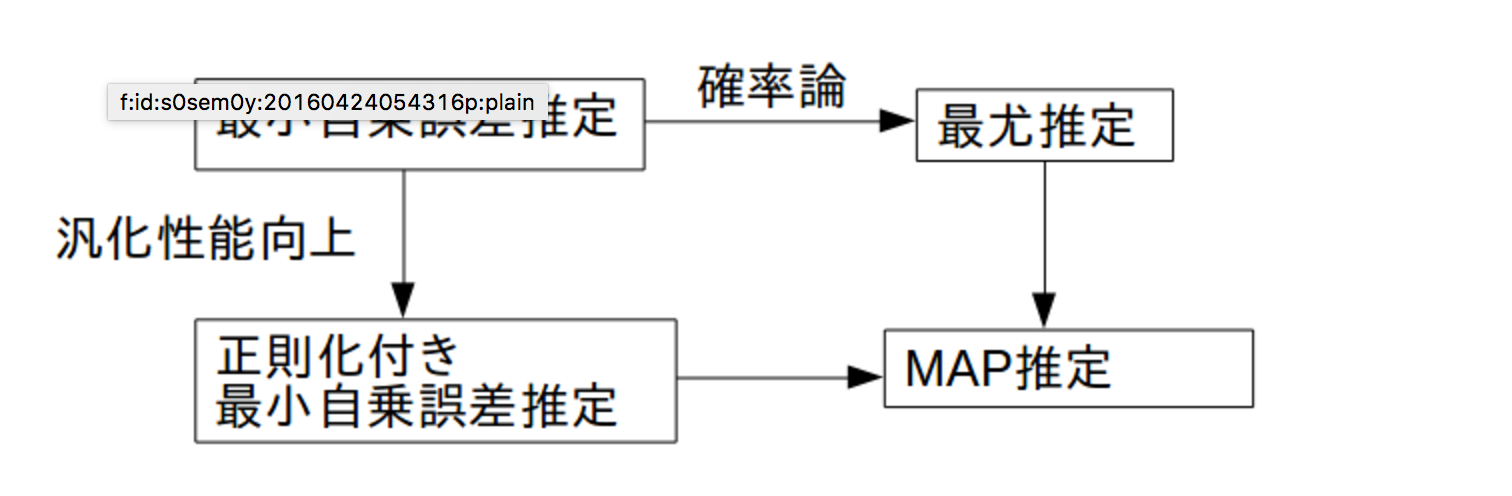
最尤推定、MAP推定は、二条和誤差推定、二条和誤差推定+正則化項を確率論へ落とし込んだものと考えても良い。
from : http://s0sem0y.hatenablog.com/entry/2016/04/24/055832
1.2.6 ベイズ曲線フィッティング
MAP推定では事後確率が最大となるパラメータを点で決めて予測分布の式に代入していた。
ベイズ推定によるフィッティングは$\boldsymbol{w}$に関して周辺化して予測分布を求めるのが特徴。
予測分布は
p(t|x,\boldsymbol{x},\boldsymbol{t})=\int p(t|x,\boldsymbol{w})p(\boldsymbol{w}|\boldsymbol{x},\boldsymbol{t})d\boldsymbol{w}=\mathcal{N}\bigr(t|m(x),s^2(x)\bigr)
で与えられる
平均と分散は
m(x)=\beta\boldsymbol{\phi(x)}^T\boldsymbol{S}\sum_{n=1}^N\boldsymbol{\phi(x_n)}t_n
s^2(x)=\beta^{-1}+\boldsymbol{\phi(x)}^T\boldsymbol{S}\boldsymbol{\phi(x)}
となり、行列$\boldsymbol{S}$は
\boldsymbol{S}^{-1}=\alpha\boldsymbol{I}+\beta\sum_{n=1}^N\boldsymbol{\phi(x_n)}\boldsymbol{\phi(x_n)}^T
で与えられる。
ここで$\boldsymbol{I}$は単位行列で、$\boldsymbol{\phi(x)}$は$\phi_i(x)=x^i(i=0,...,M)$という要素を持つベクトルを定義した。
予測分布の分散や平均は$x$に依存していることがわかる。
以下は人工的に作った正弦曲線の回帰問題の予測分布である。
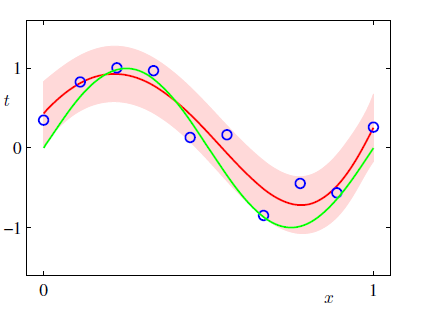
点ではなく予測分布の形になっている。
http://aidiary.hatenablog.com/entry/20100404/1270359720
1.3 モデル選択
最小二乗法で多項式曲線をあてはめた例で、最も良い汎化性能を示した最適な次数の多項式があることを見た(p7:図1.5など)。多項式の次数($\boldsymbol{w}$)はモデルの複雑さに対応していて、正則化係数$\lambda$は複雑さを制御している。また混合分布やニューラルネットワークなどはさらにそのパラメータが多い。
我々はデータに対して最も良い予測をするために、適切なパラメータの値を決めなければならない。
過学習の問題に対応するため、訓練のためのデータで学ばせモデルを作った後、検証用のデータを使ってそのモデルを評価する必要がある。
しかしデータは限られており、沢山訓練させると、検証用データが少なくなりそのモデルがイケてるものか判別しづらくなる。
どないしよ→交差確認という方法がある
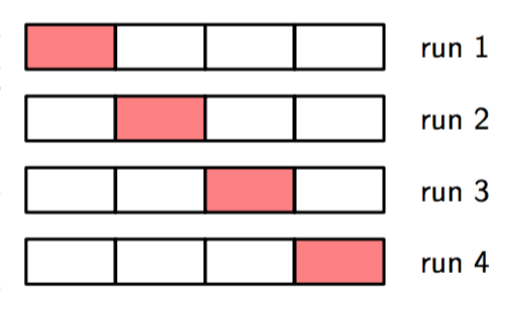
すべてのデータを1/Sに分割して訓練と検証をローテーションさせてく方法
欠点は訓練回数がSに比例して増えること。
また、複数の複雑さパラメータをもつ(データの次元数が多いときなど)場合、指数関数的に訓練回数が増える可能性がある。
→1回の訓練だけで複数の超パラメータとモデルのタイプを比較できたら最高!
→よりよいモデルを選択するための規準→「情報量規準」
わかりにくい!
例として)章1.1において、$M=9$だとよろしくなさそうと直感的にわかった。それをよろしくなさそうと示してくれるのが情報量規準。
AIC(赤池情報量規準)
http://www.sigmath.es.osaka-u.ac.jp/shimo-lab/ja/research-new/model-selection/
http://takashiyoshino.random-walk.org/memo/keikaku2/node5.html
その変種のBIC(ベイズ情報量規準)もある
→4.4.1でやるようです。
1.4 次元の呪い
次元の呪いとはデータの次元数が大きいと効率的に機械学習をさせることが難しくなることをいう。
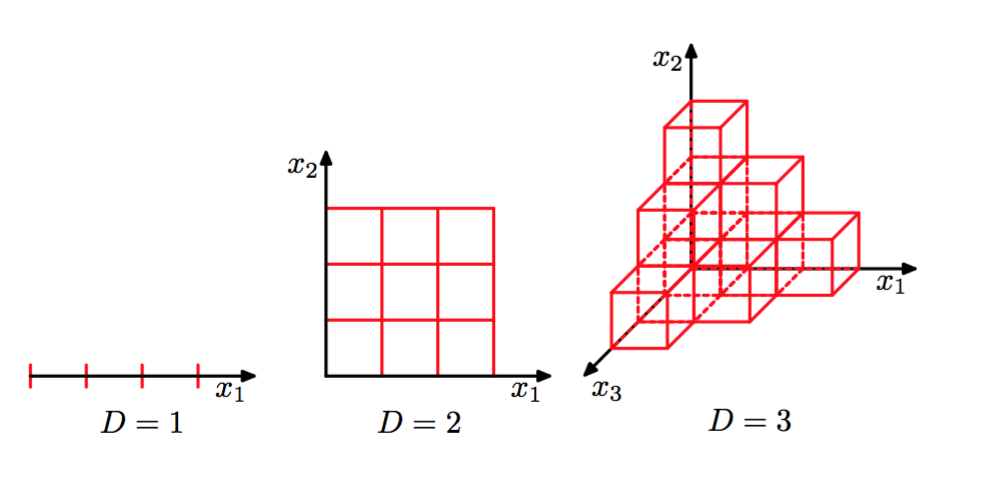
ココらへん見ていきましょう。
http://s0sem0y.hatenablog.com/entry/2016/04/15/004738
https://www.techcrowd.jp/machinelearning/dimensions/
http://roadtomachinelearning.blogspot.jp/2012/10/blog-post_24.html
引用
PRML