pytorchを使った関数のフィッテング

はじめに

以下で、pytorchを使って線形回帰をやってみたが、もう少し複雑な関数を使って、自動微分と最適化の動作を確認する。

求める関数

以下のような、二次関数($5x^2+6x+7$に乱数を加えたもの)を再現できるか試してみる。

コード

import numpy as np
import torch
import matplotlib.pyplot as plt

xi = np.arange( -10, 11, 1. )
yi = 5*xi**2 + 6*xi + 7 + np.random.normal( loc=0 , scale=50, size=len(xi) )
Xi = torch.tensor( xi )
Yi = torch.tensor( yi )

plt.scatter( xi, yi )

関数の定義

今回は、pytorch.nn.Moduleを使う。
$y=ax^2+bx+c$という二次関数でフィッテングするために、
パラメタは3つを持つ以下のようなクラスを作った。

class MyModule( torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.A = torch.nn.Parameter( torch.rand(1) )
        self.B = torch.nn.Parameter( torch.rand(1) )
        self.C = torch.nn.Parameter( torch.rand(1) )
    def forward(self, x):
        return self.A*x**2 + self.B*x + self.C

ポイントは、torch.nn.Paramete()で、パラメタとなる変数を登録するところ。

これにより、自動微分で傾き(grad)が求まるので、オプティマイザが変数の最適化を実行することができるようになる。

学習については、イデオム通り。

# モデルの生成
net = MyModule()

# オプティマイザにパラメタを登録
optim = torch.optim.RMSprop(net.parameters(), lr=0.001)

# 誤差計算用
mseloss  = torch.nn.MSELoss()

# 学習
for i in range(7000):
    # パラメタ(A,B,C)に格納されている、傾きをゼロクリア
    optim.zero_grad()

    # 予測値を計算
    Y = net(Xi)

    # 予測値(Y)と正解ラベル(Yi)の誤差を計算
    loss = mseloss( Y, Yi )

    # 自動微分で各パラメタ(A,B,C)の傾きを計算
    #  → A,B,Cの微小変化がlossにどう影響するか算出
    loss.backward()

    # 求まった傾きを使って、パラメタ(A,B,C)を更新
    optim.step()

print( net.A , net.B , net.C )

Parameter containing:
tensor([5.0715], requires_grad=True) Parameter containing:
tensor([4.6012], requires_grad=True) Parameter containing:
tensor([6.2303], requires_grad=True)

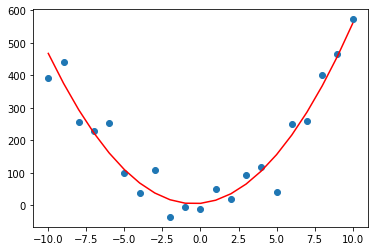
元の関数は、A=5,B=6,C=7なので少しずれているが、グラフにすると以下なので大体あっていそう。(摂動を与えた分のずれが見えている様子)

結果表示

plt.scatter(xi,yi)
Y = net(Xi)
plt.plot( xi , Y.detach().numpy() , color="red" )