この記事は統計・機械学習の数理 Advent Calendar 2023 の1日目の記事です。

1.背景

ベイズ統計学を勉強する際に基本となる条件付き確率$$P(A|B) = \frac{P(A\cap B)}{P(B)}\label{1}\tag{1}$$とそれを式変形して導かれる確率の乗法定理$$P(A\cap B) = P(A|B)P(B)\label{2}\tag{2}$$これらの式は当たり前のように道具として使用しているのですが、ふとした瞬間に「この式は何を意味しているのだろうか？」と疑問になることがありました。
ベン図を用いて$(\ref{1})$, $(\ref{2})$ を整理するとそれぞれの式のイメージが掴めた気がするので自分なりの理解をメモとして残しました。
この記事を投稿するにあたって、既に同じような内容を書いてる方がいらっしゃるのではと思い検索したところ、Qiitaでは既に、わかりやすい記事が存在したため、わざわざ自分が記事にする必要はないとも考えたのですが

Web上に何か記事を残してみたい
アドカレに参加してみたい
他の条件付き確率の記事も読んでみるきっかけになるかもしれない

の理由から記事として残すことにしました。(似た内容の記事は他にもあるかも)

2. この記事を読むにあたって

以下の知識を前提としています。

高校数学で学ぶ "場合の数"の分野
数理統計学の基礎の部分

また、解釈を重視した結果、文章中に数学的に正しくない表現をしているであろう箇所があります。「こういう注釈をつけた方がいいよ」と教えていただける方がいらっしゃいましたら、コメントいただけますと幸いです。
また、表現についても「こっちの方がわかりやすいのでは？」と提案していただける方がいらっしゃいましたら気軽にコメント下さい。

3. 条件付き確率のイメージ

再掲しますが、条件付き確率$P(A|B)$は、ある事象$B$が起こったという条件のもとで、別の事象$A$が起こる確率を表し、以下の式で定義されます$$P(A|B) = \frac{P(A \cap B)}{P(B)} \tag{1}$$この定義式ではなぜ$P(B)$で割り算を行っているのでしょうか？確率の割り算とは何を表しているのでしょうか？
この記事では確率$P(B)$で割るとはどういう意味なのかを考えて見たいと思います。

3.1. 確率を場合の数で考える

問題提起のために先に確率を登場させてしまいましたが、標本空間$\Omega$における、事象Aが起こる確率を以下のように確率を定義します。¹
$$P(A) = \frac{n(A)}{n(\Omega)} \label{3}\tag{3}$$ここで、$n(A) =事象Aの場合の数$ とします。
ベン図を用いて表すと、確率$P(A)$は、赤い斜線部分 / 青い塗りつぶし部分となります。(見えにくいですが、赤い斜線部分にも青の塗りつぶしはされています)

3.2. 条件付き確率を場合の数で考える

($\ref{3}$) のように場合の数で条件付き確率の式($\ref{1}$)を考えてみましょう。以下のように書けます。
$$P(A|B)= \frac{P(A\cap B )}{P(B)} = \frac{\frac{n(A\cap B)}{n(\Omega)}}{\frac{n(B)}{n(\Omega)}} = \frac{\frac{n(A\cap B)}{\cancel{n(\Omega)}}}{\frac{n(B)}{\cancel{n(\Omega)}}} =\frac{n(A\cap B)}{n(B)} \label{4}\tag{4}$$($\ref{4}$) では、$n(\Omega)$が打ち消されることで、分母が$n(B)$となっています。

こちらもベン図を用いて表すと以下のようになります。確率$P(A)$の時と同じく、確率$P(A|B)$は、赤い斜線部分 / 青い塗りつぶし部分になります。

($\ref{4}$)とベン図をよく照らし合わせてみて欲しいのですが、確率$P(A|B)$の分母は$n(B)$なので、青の塗りつぶし部分が標本空間全体の$\Omega$でなく、事象$B$になっています。

誤解を恐れずにイメージを言うと、分母が$n(B)$であるということは、$B$ を基準とした確率であると考えられます²。 同様に、確率$P(A)$のように分母が$n(\Omega)$であるということは、$\Omega$を基準とした確率であると考えられます。

以上を踏まえると、$P(A|B)$の定義である「Bの元で、Aがおきる確率」という状態のイメージをなんとなく掴めるのではないでしょうか？

4. 確率の乗法定理のイメージ

$P(A|B)$のイメージをベン図を用いて掴めたところで乗法定理 $$P(A\cap B) = P(A|B)P(B)\label{5}\tag{5}$$ についても考えてみたいと思います。

$P(A|B)$と$P(A\cap B)$の関係を図示すると以下のようになっています。
左のベン図が$P(A|B)$、右のベン図が$P(A\cap B)$です。

relation_prob_a_given_b_and_prob_b_given_a

($\ref{5}$)より、$P(A\cap B)$は$P(A|B)$と$P(B)$の積で得られますが、$P(A|B)$は事象$B$が基準となっている確率であり$\Omega$が基準の確率でないから、$\Omega$が基準となっている確率$P(A\cap B)$にするためには、$P(B)$をかけて基準を変えてあげる必要があります。(青の塗りつぶし部分を$\Omega$全体に広げてあげる必要がある)
式で考えると以下のような感じでしょうか。分母が$n(B)$である$P(A|B)$に$P(B)$をかけることで、分母を$n(\Omega)$にしています。
$$P(A|B)P(B) = \frac{n(A\cap B)}{\cancel{n(B)}} \cdot \frac{\cancel{n(B)}}{n(\Omega)} = \frac{n(A\cap B)}{n(\Omega)}=P(A\cap B)\label{6}\tag{6}$$

逆に$P(A\cap B)$から$P(A|B)$を手に入れる場合³、$P(A\cap B)$は$\Omega$が基準となっている確率であるため、$B$が基準である$P(A|B)$にするためには、$P(B)$で割って基準を変えてあげる必要があります。(青の塗りつぶし部分をBに縮めてあげる必要がある)
こちらも式で考えると以下のようになります。$P(B)$で割ることによって分母を$n(B)$にしています。

$$\frac{P(A\cap B)}{P(B)} = \frac{n(A\cap B)}{\cancel{n(\Omega)}}\cdot \frac{\cancel{n(\Omega)}}{n(B)} = \frac{n(A\cap B)}{n(B)} = P(A|B)\label{7}\tag{7}$$

5. ベイズの定理のイメージ

$A_1, \cdots,A_n$を標本空間 $\Omega$ の分割であるとします⁴。
$\Big($つまり、全ての$k \neq l$で$A_k\cap A_l = \phi$ かつ、$\bigcup_{k=1}^n A_k=\Omega$ が成立するとします$\Big)$
このとき、事象$B$を与えたときの$A_k$の条件付き確率$P(A_k|B)$は以下の式で求めることができ、これをベイズの定理と言います。
$$P(A_k|B) = \frac{P(B|A_k)P(A_k)}{\sum^n_{k=1}P(B|A_k)P(A_k)}\label{8}\tag{8}$$この式もベン図を用いてイメージを掴んでみたいと思います。

5.1. ベイズの定理の証明

この章の流れとしてはまず、ベイズの定理を証明し、その後証明で登場する式のイメージをベン図で表しながらベイズの定理の主張がどのようなイメージになるかを考えたいと思います。(なるべく省かずに記述するので、必要ない部分は適宜読み飛ばして下さい)

証明

\begin{align}
&証明は条件付き確率の定義\ P(A_k|B) = \frac{P(A_k\cap B)}{P(B)}から出発します。 \tag{A}\\\\
&確率の乗法定理より、P(A_k \cap B) = P(B|A_k)P(A_k)が成立します。 \tag{B}\\\\
&A_1\cap B, A_2\cap B, \cdots , A_n\cap B\ はそれぞれ排反であるから、\\
&P(B) = \sum^n_{k=1} P(A_k\cap B) = \sum^n_{k=1}P(B|A_k)P(A_k)が成立します。\tag{C}\\\\
&(A),(B),(C)より、P(A_k|B) = \frac{P(A_k\cap B)}{P(B)} = \frac{P(B|A_k)P(A_k)}{\sum^n_{k=1}P(B|A_k)P(A_k)}が得られます。
\end{align}

証明とイメージの照らし合わせ
証明文の(A)からイメージしてみましょう。条件付き確率$P(A_k|B)$をベン図で表すと以下のようになります。
くどいですが、$P(A_k|B)$は赤い斜線部分 / 青い塗りつぶし部分です。

なお、$P(A_k|B) = \frac{P(A_k\cap B)}{P(B)}$なので、$P(A_k|B)$を求めるには、$P(A_k\cap B)$と$P(B)$の値がわかれば良いことになります。

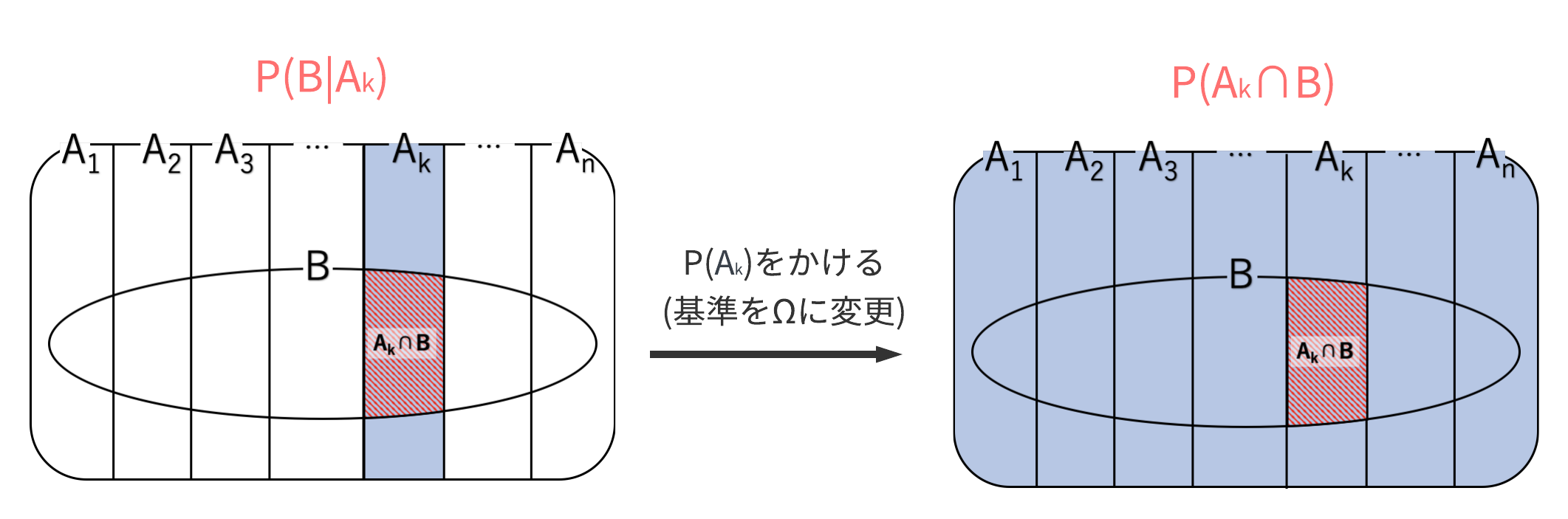
次に(B)についてイメージして見ましょう。$P(B|A_k)$から$P(A_k\cap B)$を手に入れますが、$P(B|A_k)$は$A_k$を基準とした確率であるため、$\Omega = \bigcup_{k=1}^n A_k$が基準である$P(A_k\cap B)$にするためには$P(A_k)$をかけて基準を変えてあげる必要があります。
$$P(B|A_k)P(A_k) = \frac{n(B\cap A_k)}{\cancel{n(A_k)}} \cdot \frac{\cancel{n(A_k)}}{n(\Omega)} = \frac{n(A_k\cap B)}{n(\Omega)}=P(A_k\cap B) \label{9}\tag{9}$$

最後に(C)について考えましょう。複雑そうに見えますが、やっていることは$P(B)$を計算しているだけです。
ここで、まず$P(B)$がどうなっているかをベン図で図示してみましょう。

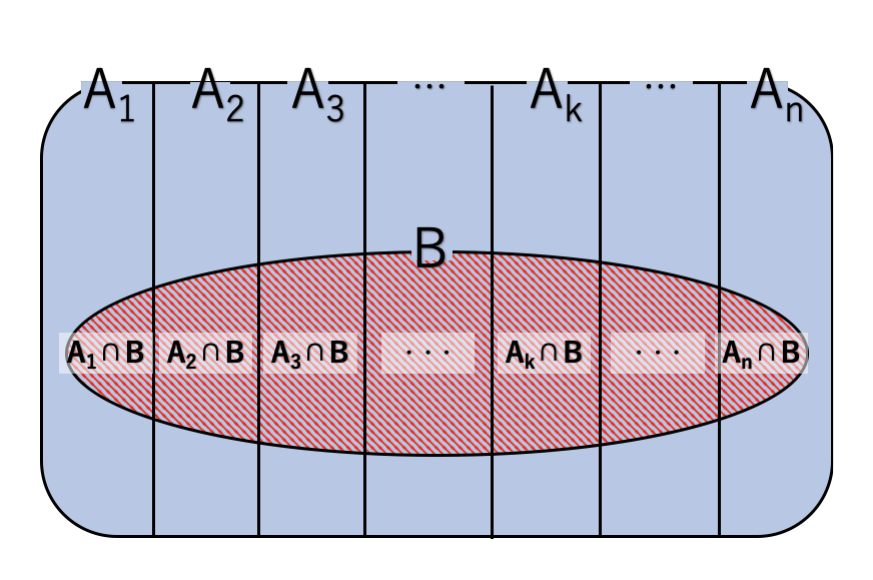
ここで、図で表している通り、$B = \bigcup_{k=1}^n A_k \cap B$が成立し、全ての$k\neq l$について、$A_k\cap B$と$A_l\cap B$は排反であるから、
$$P(B) = P(A_1\cap B) + P(A_2\cap B) + \cdots P(A_n\cap B) = \sum^n_{k=1}P(A_k\cap B) \label{10}\tag{10}$$が成立します。

ここで、($\ref{9}$)でより、$k\in [1,...,n]$について、以下が成立しているので、
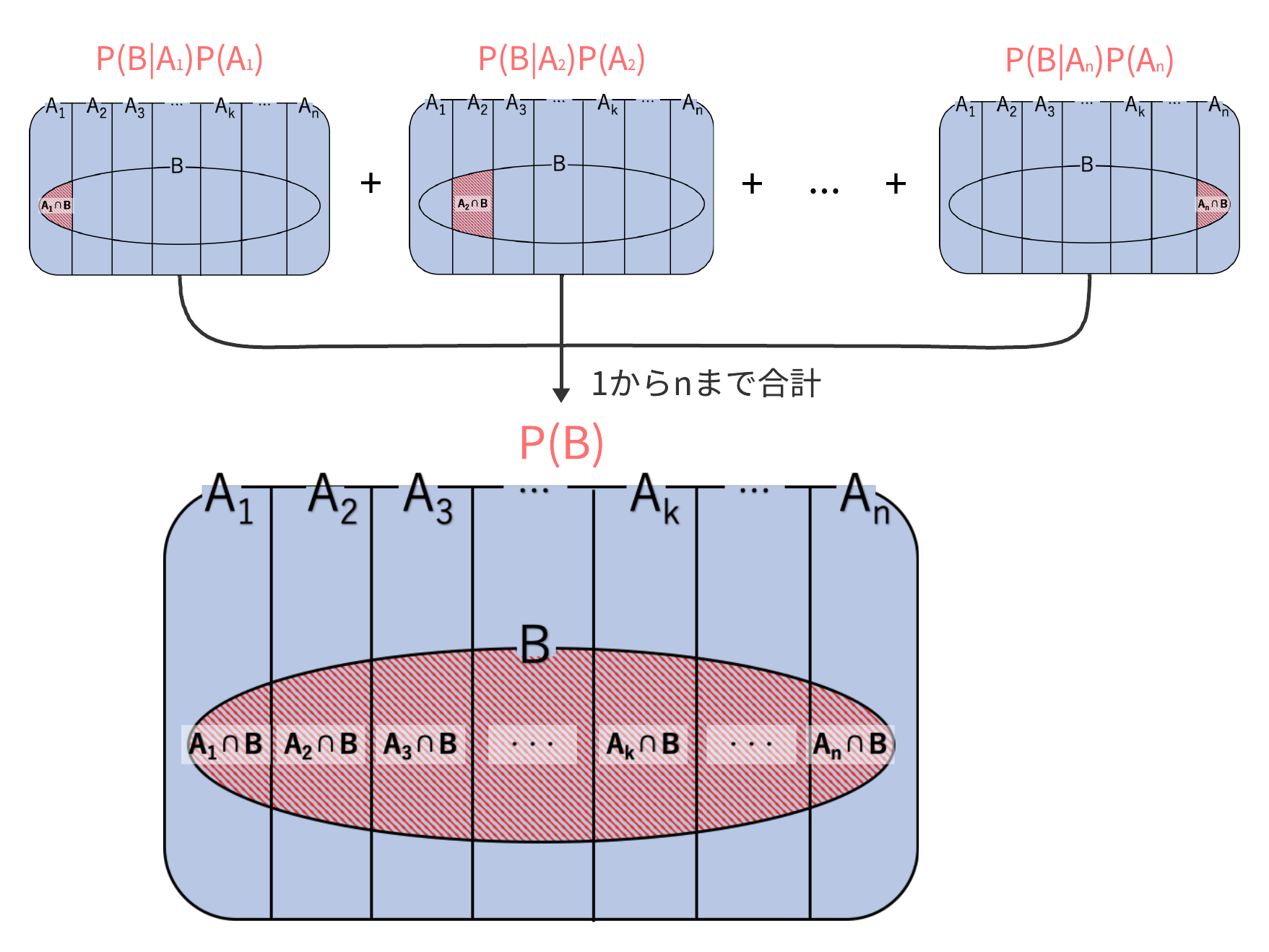
$$P(A_k\cap B) = P(B|A_k)P(A_k)$$$P(B)$を次のように書き換えることができます。
$$P(B) = \sum^n_{k=1}P(A_k\cap B) = \sum^n_{k=1}P(B|A_k)P(A_k)\label{11}\tag{11}$$ 式($\ref{11}$)のイメージは以下のようになります。$A\cap B$を$n$個に区切ったものを全て足し合わせているイメージです。

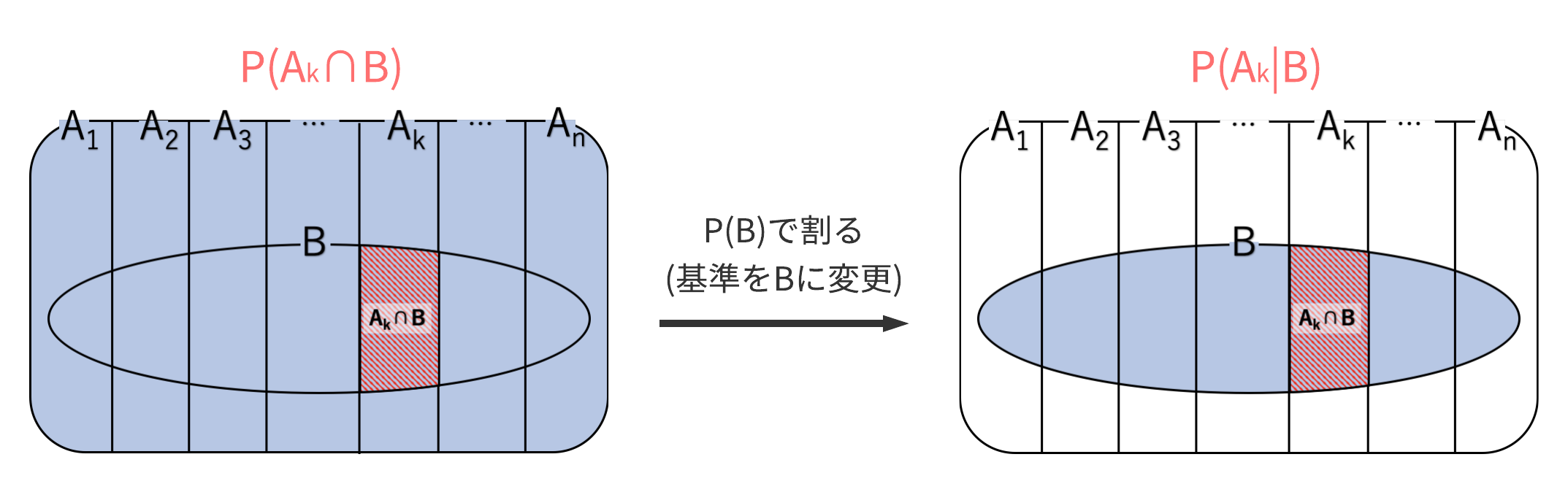
(B),(C)より、$P(A_k\cap B)$の値と、$P(B)$の値がわかったので、$P(A_k\cap B)$を$P(B)$で割ることで
$$P(A_k|B) = \frac{P(A_k\cap B)}{P(B)}$$が得られます。

おわりに

いかがだったでしょうか？
わかりやすくしようと色々と書いた結果、逆にわかりにくくなってしまったかもしれませんが、少しでも条件付き確率に関するイメージが湧けば嬉しいです。
機会があれば次は条件付き確率密度関数についても同じような記事が書ければいいなと思っています。

確率木という考え方があるらしいですね。計算するならこっちのほうが簡単そうです。(去年の統計学 Advent Calendar 2022)

参考

以下の記事、書籍を参考にしました。

現代確率論だともっと厳密な定義されているそうです。いつか測度論も勉強しなければ。 ↩
別のイメージとしては「$P(A\cap B)$を$P(B)$で割ることで、標本空間を$\Omega$から$B$に変更、事象$A$を事象$A\cap B$に変更したと考えられる」ということでしょうか(本文に書いたイメージもこのイメージも数学的に合っているのかはわかりません) ↩
= 条件付き確率の定義なので3.2.の内容と同じですが、一応メモ ↩
標本空間$\Omega$を重なりがないように分割するイメージ ↩

条件付き確率と確率の乗法定理のイメージを掴みたい