はじめに
E資格対策のため、応用数学を勉強していたのですが、「条件付き確率」がなかなか覚えられませんでした。（どちらがAかBか分からなくなる)
ベン図を使って視覚的に理解すると忘れにくそうなので、理解過程をメモしておきます。
条件付き確率の公式
事象Aが起こる条件で、事象Bが起こる確率は、次のような式になります。
$$ P(B|A) = \frac{P(A \cap B)}{P(A)} $$
事象Bが起こる条件で、事象Aが起こる確率は、次のような式になります。
$$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$
AとBが入り乱れて、数式で覚えられませんでした。
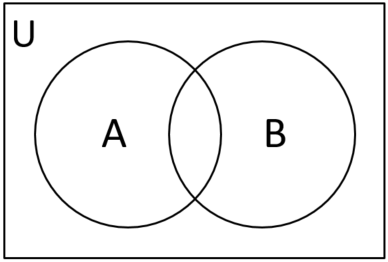
ベン図で理解する
全事象をU、各事象をA,Bとしたベン図です。
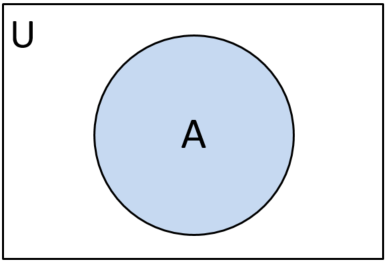
事象Aの確率
事象Aの確率 $ P(A)$ は、$ 事象A \div 全事象U $ なので、
$$ P(A) = \frac{A}{U} $$
となります。
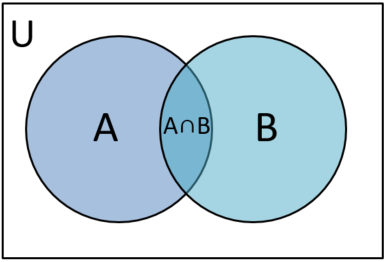
事象Aと事象Bの積集合の確率
積集合の確率 $ P(A\cap B)$ は、$ 積集合 \div 全事象U $ なので、
$$ P(A\cap B) = \frac{A\cap B}{U} $$
となります。
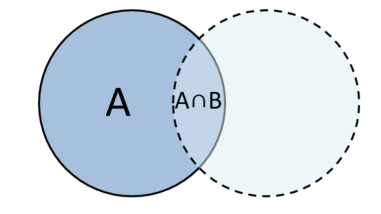
条件付き確率
条件付き確率 $ P(B|A)$ は、事象Aの範囲内で事象Bが起こった確率なので、$ 積集合 \div 事象A $ となります。
$$ P(B|A) = \frac{A \cap B}{A} $$
右辺の分母と分子に全事象Uを割れば、条件付き確率の公式になります。
$$ P(B|A) = \frac{ \frac{A \cap B}{U}}{ \frac{A}{U}} $$
$$ P(B|A) = \frac{P(A \cap B)}{P(A)} $$
参考
下記の動画を参考にしました。
数学Ａ基礎講座「条件付き確率とベイズの定理」