ベイズの定理はGoogle検索アルゴリズムやロボット自己位置推定などにも使われていますが、中々ややこしい定理なので理解しづらい。そこで、自分なりの解説をアップしました。
※ 曖昧な表現を避けるため、同じことを何度もくどく書いていますが、随所随所読み飛ばしOKです。
ベイズの定理の目的と意味
ベイズの定理とは、2種類の確率が影響を及ぼし合う時の話です。「〇〇が起きる確率」と「△△が起きる確率」で話を進めましょう。
まずベイズの定理は何のためにあるのかと言うと、
“△△が起きたっていう前提条件を加えると、〇〇が起きる確率は(ただ単純に〇〇だけが起きるときの確率と比べて)何%に変化するのかを知るため”
です。
ただ単純に〇〇だけが起きる確率ではなく、△△っていう新たなヒントもしくは前提条件が加わると、それに影響されて〇〇が起きる確率は上がったり下がったり変化するわけです。
でも「△△が起きた状況下での〇〇が起きる確率」ってのは直接測ったり直接計算したりするのが難しい、だからちょっと間接的に求めてみましょ、っていうツールがベイズの定理です。
文字の意味を図で理解しよう
よく使われる文字の意味をしっかり見ていきましょう。
① P(〇〇)…単に〇〇だけが起きる確率。
② P(△△)…単に△△だけが起きる確率。
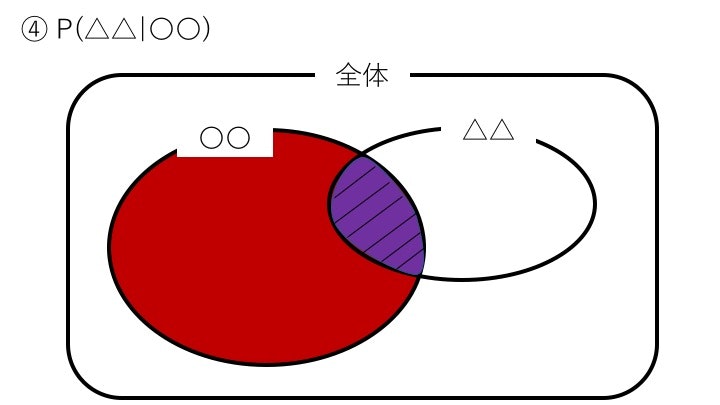
③ P(〇〇|△△)…△△が起きたと仮定した後に、〇〇が起きる確率。
④ P(△△|〇〇)…〇〇が起きたと仮定した後に、△△が起きる確率。
(縦棒 | の前が求めたい確率で、縦棒 | の後ろが前提条件です。英語と同じ語順だと思うと覚えやすいかと)
⑤ P(〇〇 ∩ △△), P(△△ ∩ 〇〇)…〇〇が起きて、かつ△△も起きる確率。
この5種類の登場人物が出て来ます。
ここで注意するポイントは、
③ P(〇〇|△△)
④ P(△△|〇〇)
⑤ P(〇〇 ∩ △△)
の3者はどれも違うものであると言うことです!
よくハマりがちなのは、確率を習い始めた頃ならよくわかっていたはずの⑤ P(〇〇 ∩ △△)のことが、③ **P(〇〇|△△)**や④ P(△△|〇〇)を習うにつれて段々わからなくなっていって……
挙げ句の果てには⑤ P(〇〇 ∩ △△)のことを③ **P(〇〇|△△)**や④ P(△△|〇〇)と混同してしまうというミスです。
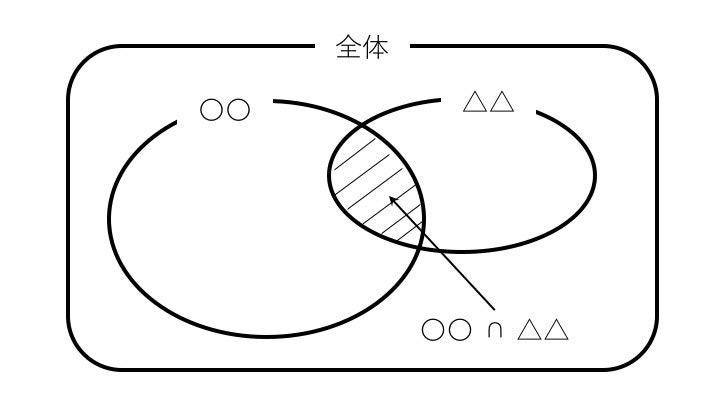
ベン図を用いて5種類の登場人物を整理してみましょう。これがデフォルトの状態です↓
このベン図↑を元に、分子は青/分母は赤という色分けで①~⑤の登場人物を図示していきます。
※ 実際は、分子の色は青と下地の赤が混ざって紫になるイメージ。
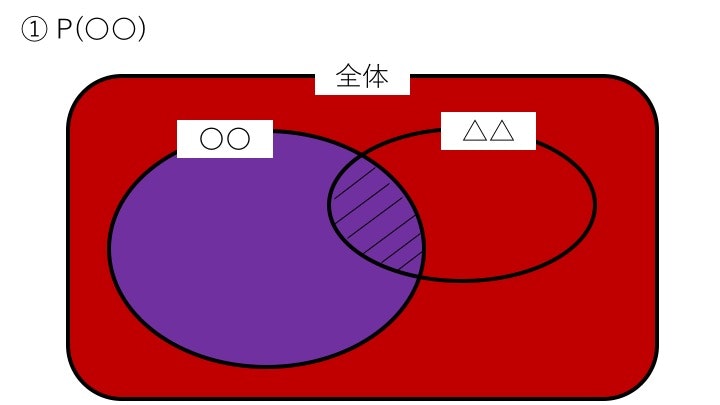
① P(〇〇)…単に〇〇だけが起きる確率
P(〇〇) = \frac{|〇〇|}{|全体|}
これは簡単ですね。
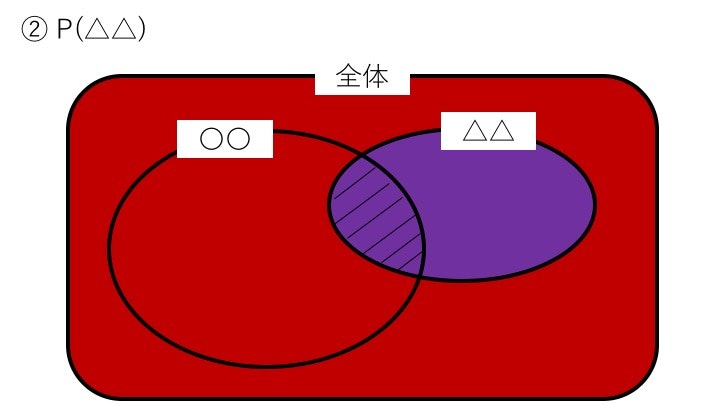
② P(△△)…単に△△だけが起きる確率
P(△△) = \frac{|△△|}{|全体|}
これも簡単ですね。
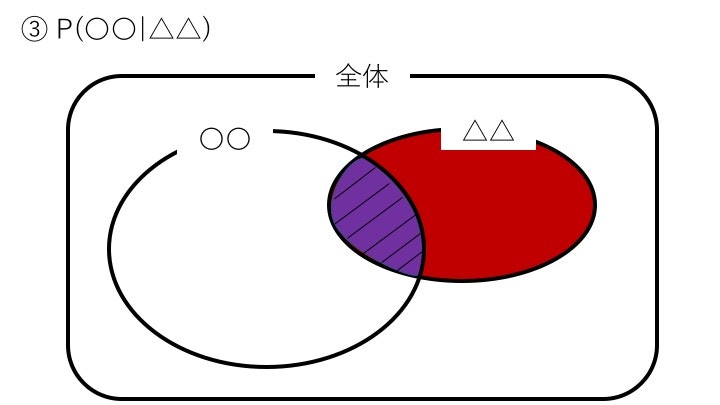
③ P(〇〇|△△)…△△が起きたと仮定した後に、〇〇が起きる確率
P(〇〇|△△) = \frac{|〇〇 ∩ △△|}{|△△|}
△△が起きたと確定してるので分母は|全体|ではなく|△△|になります。
でもその次に〇〇が起こると言っていて、結局△△も〇〇も両方起きることになるので、分子は|〇〇 ∩ △△|(図↓の斜線部分)となるのです。
④ P(△△|〇〇)…〇〇が起きたと仮定した後に、△△が起きる確率
P(△△|〇〇) = \frac{|〇〇 ∩ △△|}{|〇〇|}
〇〇が起きたと確定してるので分母は|全体|ではなく|〇〇|になります。
でもその次に△△が起こると言っているので結局〇〇も△△も両方起きることになるので、分子は|〇〇 ∩ △△|(図↓の斜線部分)となるのです。
※ これは③ P(〇〇|△△)の〇〇と△△をただ逆にしたバージョンです
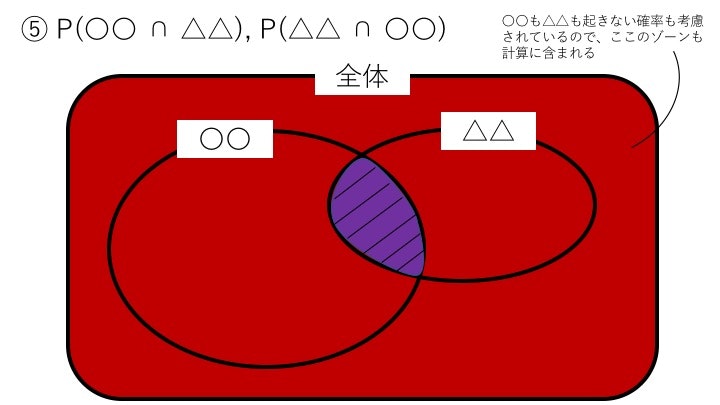
⑤ P(〇〇 ∩ △△), P(△△ ∩ 〇〇)…〇〇が起きて、かつ△△も起きる確率
P(〇〇 ∩ △△) = \frac{|〇〇 ∩ △△|}{|全体|}
〇〇が先に起きたとか、△△が先に起きたとかそういった前提条件や事前情報なしにただ単純に両者が同時に起きる確率のことです。
〇〇も△△も起きない事も考慮しているので、分母は|全体|になります。
(こいつが一番ややこしい…)
これで、③ **P(〇〇|△△)**と④ P(△△|〇〇)と⑤ P(〇〇 ∩ △△)の3者は違うものであるとわかったかと思います。
今回のベン図では、
③ P(〇〇|△△) > ④ P(△△|〇〇) > ⑤ P(〇〇 ∩ △△)
の順番で確率は低くなっていきます。これら3者とも分子は同じ|〇〇 ∩ △△|なのに分母が順に大きくなっていくからです。
③ **P(〇〇|△△)**や④ P(△△|〇〇)より、⑤ P(〇〇 ∩ △△)の方が厳しい条件なので、通常は⑤ P(〇〇 ∩ △△)の確率が一番低くなります。
よくハマりがちなミスである、これら3者を混同してしまう原因は、どれも分子が同じ|〇〇 ∩ △△|だからです。最終的な着眼点である分子が同じだから文章上だと同じ事を意味しているように見えるのですが、分母が違うから実際に数式上で計算してみると違う値が出て来る……
だからベイズ推定や条件付き確率の例題を答え合わせしたときに、「何で値が違うんや!何でこんな解き方するんや!(怒)」となるわけです(笑)
数式を用いて話を深めよう
それではここから、これら5種類①~⑤の登場人物を使って”ベイズの定理”の本題に入ります。ベイズの定理は、あの一番ややこしかった⑤ P(〇〇 ∩ △△)が中心になって話が展開されます……。
じゃあそもそも⑤ P(〇〇 ∩ △△)とは何か
⑤「〇〇が起きて、かつ△△も起きる」確率
を言い換えると、
③「△△が起きたと仮定した後に〇〇が起きる」ことに加えて、ホントに②「△△が起きる」確率
と言えます。つまり、
③「△△が起きたと仮定した後に〇〇が起きる」×②「△△が起きる」確率
ということになります。これは分数の数式で考えるとわかりやすいです。
⑤ P(〇〇 ∩ △△) = \frac{|〇〇 ∩ △△|}{|全体|}
③ P(〇〇|△△) = \frac{|〇〇 ∩ △△|}{|△△|}
② P(△△) = \frac{|△△|}{|全体|}
なので、
⑤ \frac{|〇〇 ∩ △△|}{|全体|} = {\bf ③ \frac{|〇〇 ∩ △△|}{|△△|}} × ② \frac{|△△|}{|全体|}
右辺の|△△|が約分されてます。つまり、
⑤ P(〇〇 ∩ △△) = ③ {\bf P(〇〇|△△)} × ② P(△△)
ということになるのです!
さて、これと同じ流れを〇〇と△△を逆にしたバージョン、つまり
④ P(△△|〇〇)と① P(〇〇)にも当てはめると……
⑤ P(〇〇 ∩ △△) = ④ P(△△|〇〇) × ① P(〇〇)
ということになるのです!
⑤ P(〇〇 ∩ △△)を橋渡し役として二つの世界を繋ぐ
これら2式、
⑤ P(〇〇 ∩ △△) = ③ {\bf P(〇〇|△△)} × ② P(△△)
⑤ P(〇〇 ∩ △△) = ④ P(△△|〇〇) × ① P(〇〇)
を統合すると新しく、
③ {\bf P(〇〇|△△)} × ② P(△△) = ④ P(△△|〇〇) × ① P(〇〇)
ということが言えるのです!
なんと一番ややこしかった⑤ P(〇〇 ∩ △△)を経由することによって、2つの異なった視点から話してた世界、③ **P(〇〇|△△)**と④ P(△△|〇〇)が
1つの式に繋がったのです……!これで公式の導出はほぼ終わりです。
んで、ベイズの定理の目的ってなんだっけ
ここでベイズの定理の目的をおさらいすると、
“△△が起きたって言う前提条件を加えると、〇〇が起きる確率は(ただ単純に〇〇だけが起きる確率と比べて)何%に変化するのかを計算するため”
これはまさしく③ **P(〇〇|△△)**のことです。なので、「ベイズの定理」とググって出て来るよく目にする公式はこういう形をしてるのです↓
③ {\bf P(〇〇|△△)} = \frac{④ P(△△|〇〇) × ① P(〇〇)}{② P(△△)}
右辺のただ単に〇〇だけが起きる確率① P(〇〇)は、「△△が起きた」という前提条件を加えると、それに影響されて確率③ P(〇〇|△△)に変わる。
その変化後の確率③を求めるには、前提条件である△△自体だけが起きる確率② P(△△)と、求めたい事と前提条件を逆さまにした確率④ P(△△|〇〇)が必要であるということです。
〇〇だけが起きる確率① P(〇〇)のことを事前確率 Prior Probabilityと呼び、
△△っていう前提条件の影響で変化した後の確率③ **P(〇〇|△△)**のことを事後確率 Post Probabilityと呼びます。
事前確率① P(〇〇)は、△△が起きたという前提条件や追加情報を得ると、事後確率③ **P(〇〇|△△)**に更新されるというイメージです。
不思議なようですが、事後確率③ P(〇〇|△△)自体は直接計測したりするのが難しくても、求めたい事と前提条件を逆さまにした確率④ P(△△|〇〇)の方は意外と簡単に手に入る場合が多いので、このような式が成り立ちます。
具体例 ~癌患者と喫煙者の例~
ここで理解を深めるために具体例で考えてみましょう。
↓
ベイズの定理の具体例を数式じゃなく文章と図で