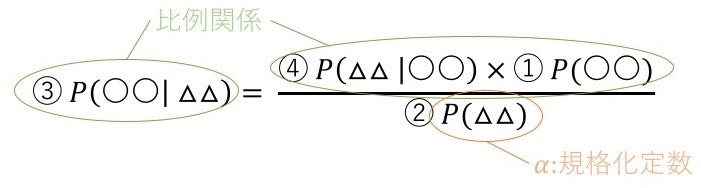ベイズの定理とはそもそも何かの解説内容を、具体例を用いて考えてみましょう。
1つの同じ問題を、正攻法での解き方と、ちょっとトリッキーな解き方の2方向から責めていこうと思います。
具体例 ~癌患者と喫煙者の例~
ここで理解を深めるために具体例で考えてみましょう。
設定
あなたは、今日診察に来る患者が癌患者かどうかを心の中で予想する変な性格の医者だとします。病院に蓄積されてる膨大な過去データより、来診患者が癌である確率は3/10(30%)だとわかっています。まあこのままだとあなたの予想は10回に3回当たったり外れたりするだけですが、ここで、
「今日来る患者は喫煙者であるらしい」
との情報をゲットしました。
患者が喫煙者だということを聞くと、その患者が癌である可能性が単なる3/10(30%)から上がるような気がしませんか?その感覚を計算式に落とし込んだのがベイズの定理なのです。
計算して確率を推定してみる
では実際に計算してみましょう。使う式はこれ↓です。
③ {\bf P(x=C|x=S)} = \frac{④ P(x=S | x=C) × ① P(x=C)}{② P(x=S)}
① P(患=Cancer)…患者が癌である確率。
↓
病院に蓄積された膨大な過去データにより3/10(30%)とわかっている。
② P(患=Smoker)…患者が喫煙者である確率。
↓
全国調査によると、2/10(20%)だとわかっている。
③ P(患=Cancer|患=Smoker)…患者が喫煙者だと仮定した後に、その患者が癌である確率。
↓
これが今回求めたい値。
④ P(患=Smoker|患=Cancer)…患者が癌だと仮定した後に、患者が喫煙者である確率。
↓
これは、既に癌にかかっている患者達に病院でアンケートを取れば簡単に得ることができる値で、アンケート結果は6/10(60%)だった。この病院では癌患者の過半数が実はタバコを吸っていたということだ……ならば逆説的だが、今日来る喫煙者の患者は癌である可能性が高くなりそうだ。このように、求めたい事と前提条件を逆さまにした確率④ P(△△|〇〇)がベイズ推定問題では必要となる。
実際にこれらの値を代入して計算すると、
\begin{aligned}
\ ③ {\bf P(x=C|x=S)} &= \frac{④ P(x=S|x=C) × ① P(x=C)}{② P(x=S)} \\
\ ③ {\bf P(x=C|x=S)} &= \frac{④ \frac{6}{10} × ① \frac{3}{10}}{② \frac{2}{10}} \\
\ ③ {\bf P(x=C|x=S)} &= \frac{9}{10}
\end{aligned}
確率は当初の30%から90%に上がった!
「患者が喫煙者だと仮定した後に、その患者が癌である確率」の答えは、③ P(患=Cancer|患=Smoker) = 9/10、つまり90%です。
当初30%だった(ただ単に)患者が癌である事前確率① P(患=Cancer)は、”その患者がタバコを吸っている”というヒントを得たおかげで事後確率③ **P(患=Cancer|患=Smoker)**に変化し、90%に上がった
……といったイメージです。
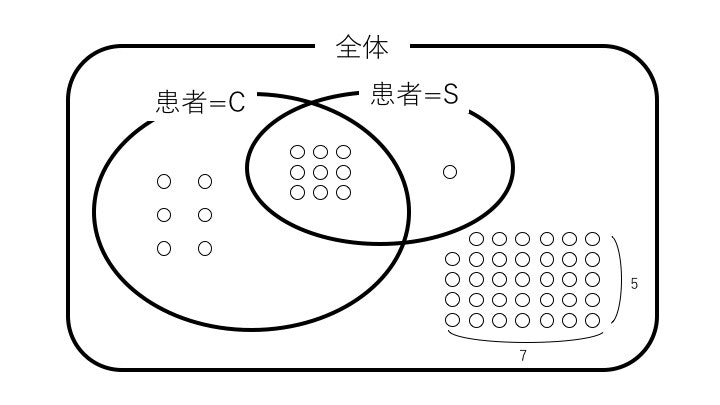
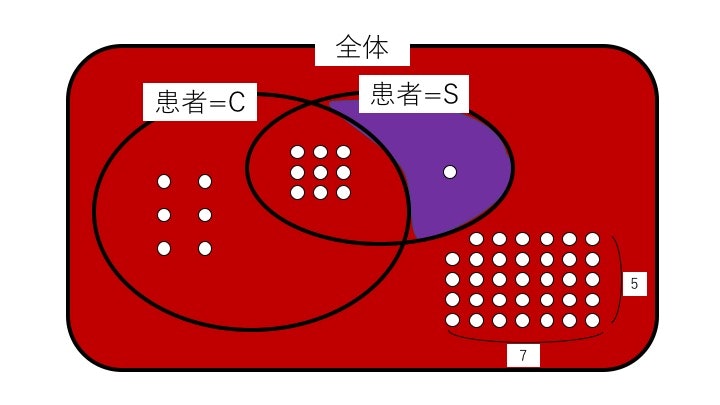
ベン図を描いてみるとこうなります。丸は患者1人分を示しています↓
分子は青/分母は赤で視覚的に分けたベン図を見ると、わかりやすいです。(実際は分子は青と赤が混ざって紫になるイメージ)↓
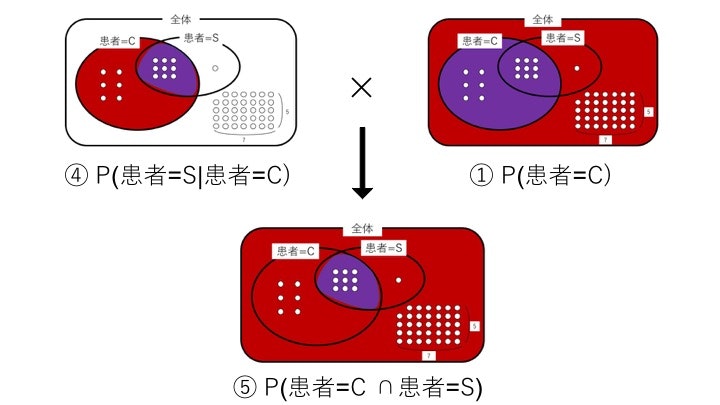
④ P(患=Smoker|患=Cancer) = 6/10 = 9/15
と
① P(患=Cancer) = 3/10 = 15/50
をかけて、
⑤ P(患=Cancer ∩ 患=Smoker) = 9/50
が一旦出てきます。
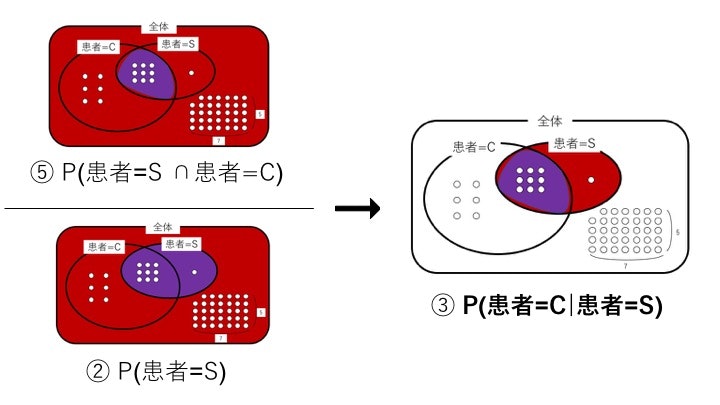
ここで
⑤ P(患=Cancer ∩ 患=Smoker) = 9/50
を
② P(患=Smoker) = 2/10 = 10/50
で割ることによって、求めたい
③ P(患=Cancer|患=Smoker) = 9/10
が出てくる……という流れです。
※ 分子が青/分母が赤です(分子の青は赤と混ざって紫になってます)。
右辺の分母が未知の時はどうする?
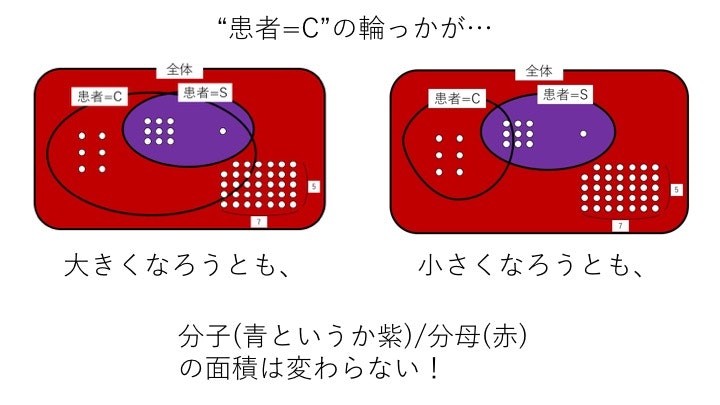
……と、ここまでが今日の来診患者が癌であるかどうかを”推定”する大まかな流れですが、一つだけ癌かどうかとは関係ない情報を使っています。それは、② P(患=Smoker)の2/10(20%)です。
② P(患=Smoker)の値は、① P(患=Cancer)の値に影響されません。② P(患=Smoker)のベン図↑で、”患者=C”の輪っかの大きさが大きくなっても小さくなっても、分子の青色(紫色)と分母の赤色の面積は変わりません。
言い換えると、(突然変異か何かで変化して)世の中の人々が癌にかかる確率が増えても減っても、タバコを吸う人は吸うし吸わない人は吸わないのです。
これは② P(患=Smoker)の値は① P(患=Cancer)の値に影響されないことを示しており、ってことは② P(患=Smoker)の値なしでも頑張れば最終的な目標である③ P(患=Cancer|患=Smoker) = 9/10を出すことができそうです。
その答えは、"できる"なのですが、そのためには新たな確率が必要となります↓
③ ’ P(患≠Cancer|患=Smoker)…患者が喫煙者だと仮定した後に、その患者が癌でない確率
この③’ P(患≠Cancer|患=Smoker)を計算で出すことによって、相対的に③ **P(患=Cancer|患=Smoker)**を出すことができるのです!
じゃどうやって③’ P(患≠Cancer|患=Smoker)を計算するかというと、また新たな確率が必要となります↓
④ ’ P(患=Smoker|患≠Cancer)…患者が癌でないと仮定した後に、患者が喫煙者である確率
↓
これは病院内のアンケート結果によると1/35(≒30%)であった。
② P(患=Smoker)の情報を知らない代わりに、新たに④’ P(患=Smoker|患≠Cancer)の情報が必要となります。しかし、この値も病院内のアンケートである程度わかるので、簡単に手に入ります。
右辺の分母なしで計算してみる
では② P(患=Smoker) = 2/10(20%)の情報なしで計算してみましょう。
まずは、ベイズの定理で③’ P(患≠Cancer|患=Smoker)を出します。② P(患=Smoker)の値はわからないのでとりあえずαとしときましょう。
③' P(x \neq C|x=S) = \frac{④' P(x=S|x \neq C) × ①' P(x \neq C)}{② a}
② P(患者=Smoker)を使わないベイズの定理実際に具体的な値を代入すると、
\begin{aligned}
\ ③' P(x \neq C|x=S) &= \frac{④' P(x=S|x \neq C) × ①' P(x \neq C)}{② a} \\
\ ③' P(x \neq C|x=S) &= \frac{④' \frac{1}{35} × ①' (1-\frac{3}{10})}{② a} \\
\ ③' P(x \neq C|x=S) &= \frac{⑤' \frac{1}{50}}{② a}
\end{aligned}
当然、分母に② αが残りますが、それで大丈夫です。
ちなみに分子の
④’ P(患=S|患≠C) × ①’ P(患≠C)
= ⑤’ P(患≠C ∩ 患=S)
= ⑤’ |患≠C ∩ 患=S|/|全体|
= 1/50
は、ベン図でいうとここです↓
↑ここに|患=S|/|全体|である② P(患=Smoker)で割ってあげれば、|患≠C ∩ 患=S|/|患=S|である③’ P(患≠Cancer|患=Smoker)が出ますね。まあ今は② αなのでわからないのですが。
同じく② P(患=Smoker)を② αとして③ **P(患=Cancer|患=Smoker)**を計算し直してみましょう。そうすると↓
\begin{aligned}
\ ③ P(x=C|x=S) &= \frac{④ P(x=S|x=C) × ① P(x=C)}{② a} \\
\ ③ P(x=C|x=S) &= \frac{④ \frac{6}{10} × ① \frac{3}{10}}{② a} \\
\ ③ P(x=C|x=S) &= \frac{⑤ \frac{9}{50}}{② a}
\end{aligned}
ここで、
③’ P(患≠Cancer|患=Smoker) = |患≠C ∩ 患=S|/|患=S|
③ P(患=Cancer|患=Smoker) = |患=C ∩ 患=S|/|患=S|
なので、
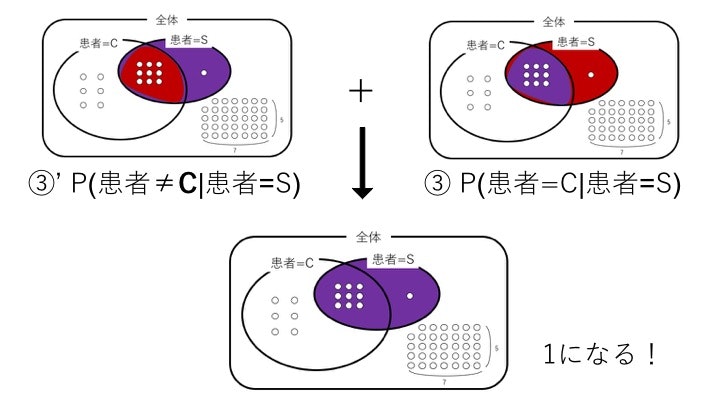
③’ P(患≠Cancer|患=Smoker) + ③ P(患=Cancer|患=Smoker)
=|患≠C ∩ 患=S|/|患=S| + |患=C ∩ 患=S|/|患=S|
=|患=S|/|患=S|
= 1
となるはずです↓
なので、
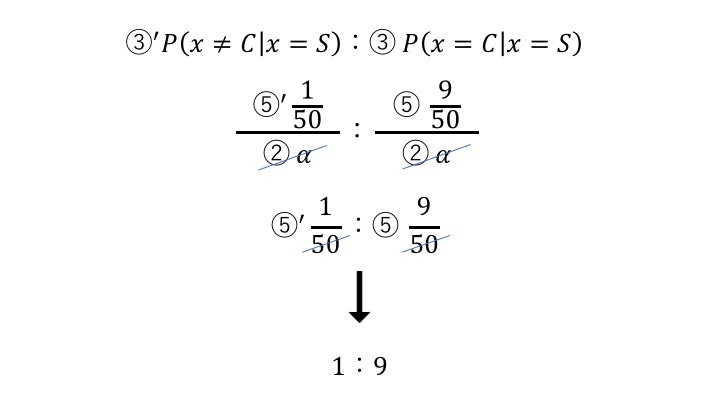
③’ P(患≠Cancer|患=Smoker):③ P(患=Cancer|患=Smoker)
の比をとってみます!すると!
③’ P(患≠Cancer|患=Smoker) が1/10(10%)で、
③ P(患=Cancer|患=Smoker) が9/10(90%)ということが
② P(患=Smoker) = 2/10(20%)の情報なしでも出せたのです!
確率の母数が常に|全体|ではないことに注意してください。母数は|患=S|になったり|患=C|になったりもします。
僕が昔ハマっていた原因は、母数の違いをわかっていなかったからです。僕も母数は常に|全体|だと勘違いしていました。
最後に
つまりベイズの定理の右辺分母の② αは実はそんなに重要じゃなくて、もっと重要なのは左辺の③ P(〇〇|△△)は右辺分子の④ P(△△|〇〇)×① P(〇〇)に比例しているということ。
比例関係であるということは、
“具体的な数値はわからないけどある程度の③ **P(〇〇|△△)**の比や傾向は、④ P(△△|〇〇)×① P(〇〇)の値で掴める”
ということです。”具体的な数値がわからない”とは、
△△が起きたと仮定した後に〇〇が起こる確率③ P(〇〇|△△)に、
△△が起きたと仮定した後に〇〇が起こらない確率③’ P(≠〇〇|△△)を
足しても合計で1(100%)にならない時があるということです……
これは事件です(汗)
そうならないためだけに、② αでベイズの定理の右辺を割ってあげなきゃいけないんです。② αで割ってあげることによって、全パターンの確率の総計が無事1(100%)に揃うわけです。
※ こういう、別に本質的なところじゃないんだけど、別に既に大小関係わかっているからもういいんだけど、でもでもやっぱり見た目のために範囲を0~1の間にキッチリ収めたい(><)ってための加工がいわゆる規格化ってやつです。
以上