Pythonで基本アルゴリズム実装：選択ソート編

選択ソートとは

• 未整列部分から最小値（または最大値）を探し、整列済み部分に移動させていくソート手法
• 配列の先頭から順に「その位置に入るべき要素」を選択していくことから「選択ソート」と呼ばれる
• 特徴
  • 計算量は O(n²) と遅い
  • 実装が比較的簡単
  • 安定ソートではない（同じ値の順序が入れ替わることがある）
• 主に学習用・教育用で使われ、実用で使われることは少ない

選択ソートの仕組み

選択ソートは、次の手順を繰り返して配列を整列させます。

1. 未整列部分の中から 最小値 を探す
2. 見つかった最小値を未整列部分の先頭と入れ替える
3. 未整列部分を一つ縮めて、再び 1 に戻る

下のgifでは、左端から順に最小値を探し、先頭と交換している様子がわかります。

---

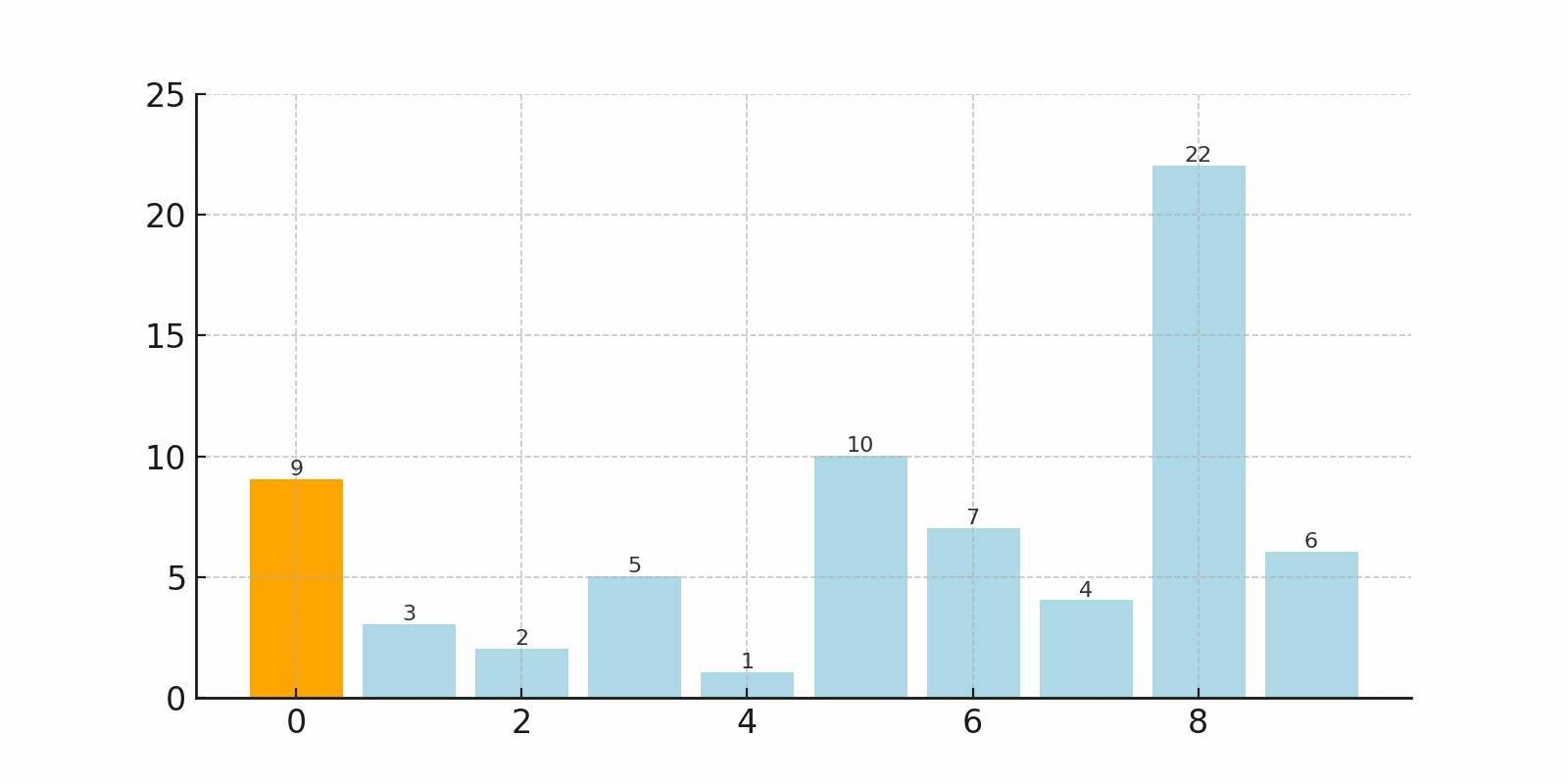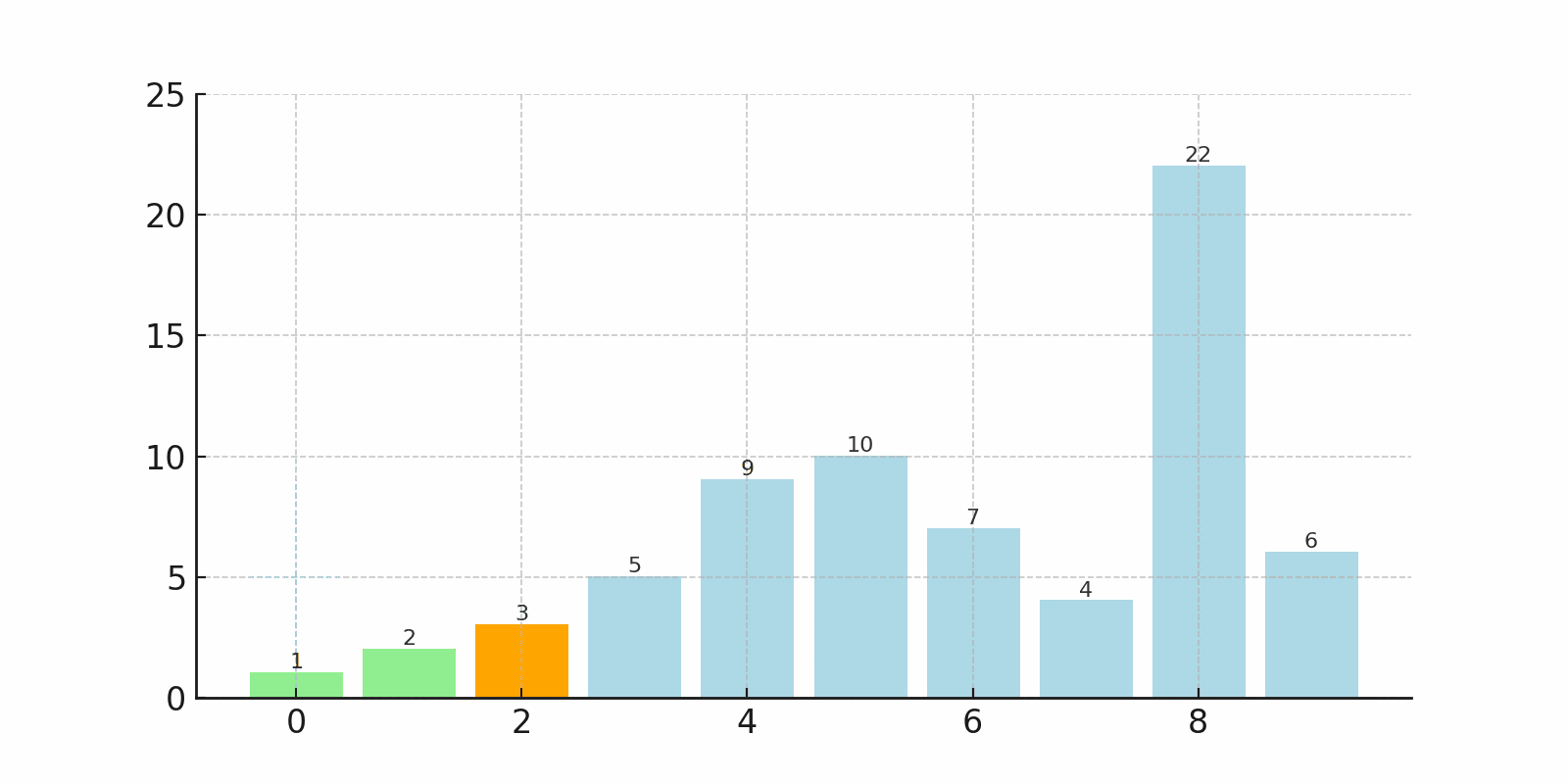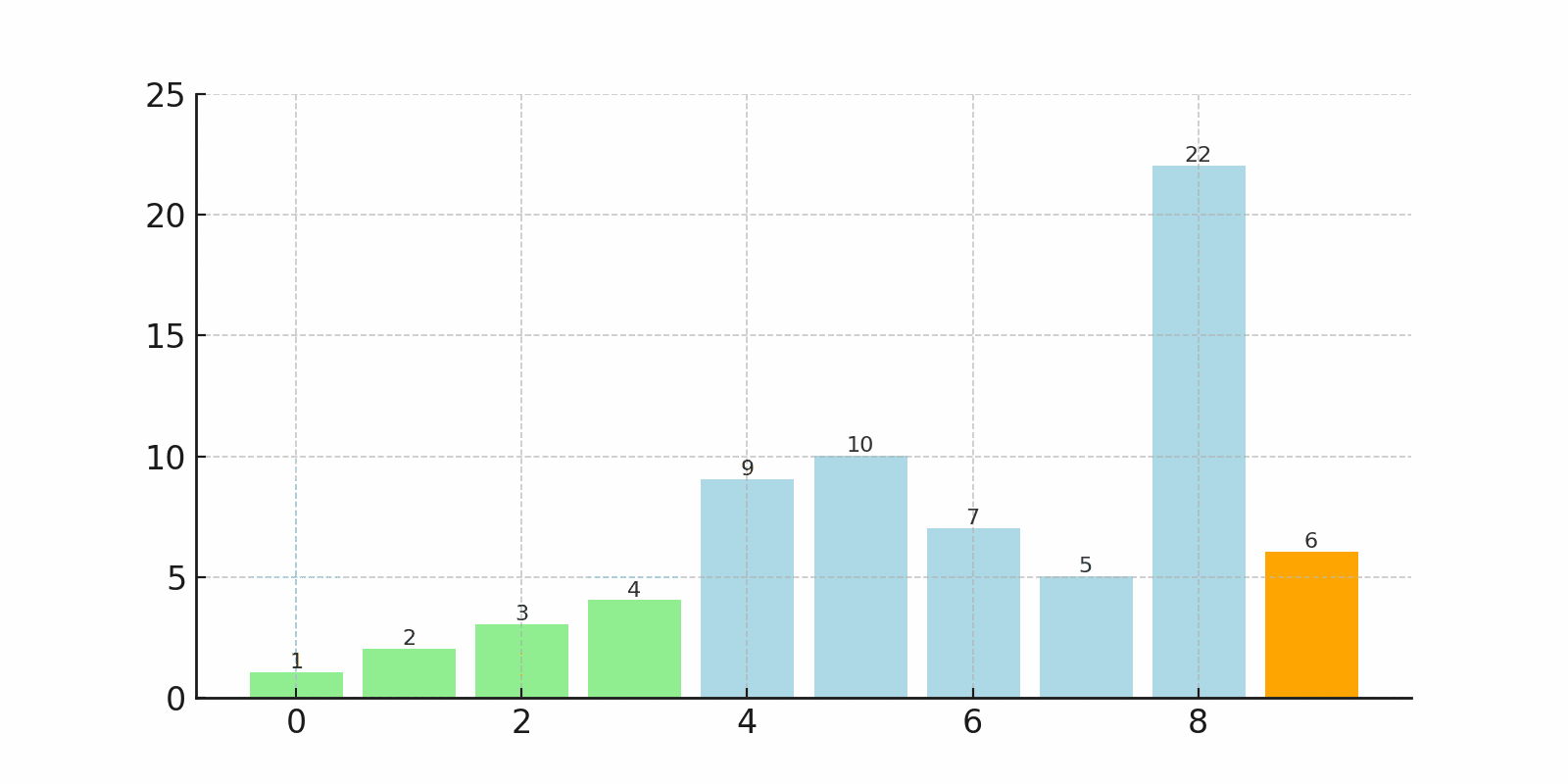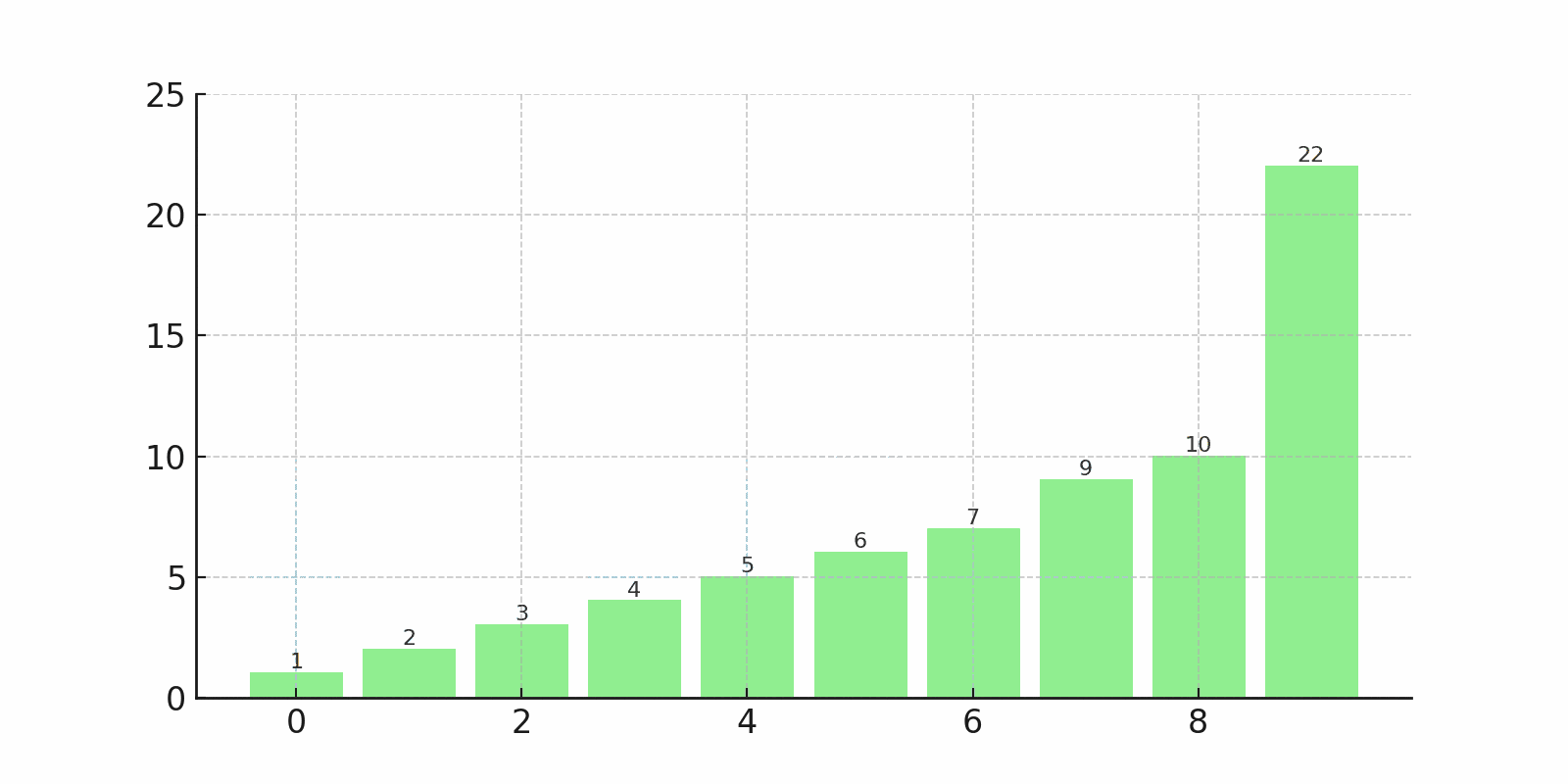
実装コード

min_indexで最小の値のindexを保持し、さらに最小の値があれば更新を行います。
そして、最小の値と未整列部分の先頭を入れ替えます。
これを繰り返すと並び替えが完了します。

def selection():
    for i in range(array_count):
        min_index = i
        for j in range(i+1, array_count):
            if array[min_index] > array[j]:
                min_index = j
        array[i],array[min_index] = array[min_index],array[i]


if __name__ == "__main__":
    array = [9,3,2,5,1,10,7,4,22,6]
    array_count = len(array) 
    selection()
    print(array)
    # [1, 2, 3, 4, 5, 6, 7, 9, 10, 22]

選択ソートの計算量について

選択ソートもバブルソートと同じく O(n²) の計算量を持ちます。

1回ごとの比較回数

配列の要素数を n とします。
選択ソートでは、各ループごとに 残りの全要素を走査して最小値を探す ため、次のように比較が行われます。

• 1回目 … n-1 回
• 2回目 … n-2 回
• 3回目 … n-3 回
• …
• 最後 … 1 回

合計はバブルソートと同じく次のようになります

(n-1) + (n-2) + ... + 2 + 1

等差数列の和で計算する

これは、1 から (n-1) までの和と同じです。

1 + 2 + 3 + ... + (n-1) = (n-1)n / 2

となります。

O(n²) になる理由

上の式はおおよそ次のように整理されます。

(n-1)n / 2 ≒ n² / 2

計算量を表すビッグオー記法では定数は無視されるため、最終的に

O(n²)

と表されます。

ただし、交換回数がバブルソートよりも基本的に少ないため、選択ソートは同じ O(n²) の中でもバブルソートより速い と言われます。