はじめに
「ポケットモンスター スカーレット・バイオレット」楽しみですね!
今回はオープンワールドで友達と一緒に冒険、それも各々の順番でジムリーダー攻略できたり夢が広がります。赤と紫というテーマも原点回帰のようで好きです。私は赤外線と紫外線関係の何かがあるのかなと妄想してます。
そんなわけで発売を楽しみにしながら剣盾で遊んでいるのですが、思い付きで紫色統一のパーティを組みました。ムゲンダイナ、カプ・レヒレ、ドラピオン、ストリンダー、オンバーン、コジョンドです。
この趣味メンバーでもなるべく勝てるように作戦を練ったものの中々勝てなかったので、対戦結果を分析して、どうすれば勝ちに繋がるかの知見に昇華しようと思います。
1. 先行研究を探す
もしポケモン対戦の分析が既にある場合、そういうwebサイトや分析ツールを使えば自分で作る必要はなくなります。あるいは既存のサービスで出来ないことがあったとしても、参考にしない手はありません。
ポケモン対戦の分析のこれまでを探した結果、少し古いものであれば存在していましたが、剣盾環境のものはありませんでした。もしかすれば実用レベルの対戦データを用意するのが難しいというのがネックになっているのかもしれません。(ニンテンドーアカウントとかに蓄積されたポケモンの対戦の記録を取得できるAPIとかが提供され始めたらいいですね)。
参考にさせて頂いたものは末尾にまとめてあります。
2. 対戦データの準備をする
2-1. データの構造を決める。
| number | column name | type |
|---|---|---|
| 1 | 対戦ID | int |
| 2 | ムゲンダイナ選出フラグ | int |
| 3 | カプ・レヒレ選出フラグ | int |
| 4 | ドラピオン選出フラグ | int |
| 5 | ストリンダー選出フラグ | int |
| 6 | オンバーン選出フラグ | int |
| 7 | コジョンド選出フラグ | int |
| 8 | 自分のダイマックスポケモン | string |
| 9 | 自分の初手選出ポケモン | string |
| 10 | 相手の禁伝の選出数 | int |
| 11 | 相手のダイマックスポケモン | string |
| 12 | 相手の初手選出ポケモン | string |
| 13 | 相手のランク | int |
| 14 | シーズン | int |
| 15 | 勝利フラグ | int |
| 16 | ザシアン選出フラグ | int |
※1 相手の禁伝の選出数は、相手の手持ちが全て判明するまでに自分が敗北した場合、その時点での判明数を格納しました。
※2 データは自分でポケモン対戦を行う様子を録画して、そこから手作業でcsvファイルに起こしました。
2-2. 備考
手作業故のサンプルデータ数の少なさ、妥当性の不安などありますが考察の都度「サンプルデータ数が少ないので~」となるのも煩わしいので一旦データを完全なものと信頼して進めていきます。
3.分析する
3-1. 環境
python 3.8.5 (venv)
matplotlib==3.5.2
optuna==2.10.1
pandas==1.4.2
scikit-learn==1.1.1
3-2. 作成したポケモン対戦結果のデータを取得する。
データを取得する際ついでに欠損値を除外しておきます。欠損値は録画ミスによって発生したもので4件ありました。
battle_results = pandas.read_csv(filepath_or_buffer='./battle_results.csv', encoding='utf_8', sep=',')
# 生データから欠損値のある行を削除する。
battle_results = battle_results.dropna()
3-3. 基本統計量を出力する。
データ数、合計、平均を確認してみます。
# データ数
battle_results_len = len(battle_results)
# 合計
battle_results_sum = battle_results.sum(numeric_only = True)
# 平均
battle_results_rate = battle_results_sum / battle_results_len
データ件数
50
sum(avg)
ムゲンダイナ選出 42 (0.84)
カプ・レヒレ選出 37 (0.74)
ドラピオン選出 22 (0.44)
ストリンダー選出 13 (0.26)
オンバーン選出 3 (0.06)
コジョンド選出 26 (0.52)
相手の禁伝の選出数 50 (1.00)
勝利数 20 (0.40)
相手のザシアン選出数 16 (0.32)
平均はそのまま比率に変換できるのでポケモンの選出についてはムゲンダイナ84%、レヒレ74%と群を抜いて高いようです。なるべくN数が多い方がいいので、この2匹以外は分析対象から足切りすることにします。というかオンバーン出番なさすぎ。。。
禁止伝説級とは平均で毎試合1体は遭遇しているようですが、意外にもザシアンが選出される率は32%でした。
ここでミスに気づいたのですが、相手のパーティにザシアンがいることと、かつ対戦に登場することは別なので、それぞれでカウントをすれば良かったです。一口にザシアン選出率32%といっても仮にパーティ自体にはいたのが80%の場合、ストリンダーがタイプ的に有利なのでけん制していたのかな、と色々考察が進んだのに勿体ありませんでした。
最後に全体の勝率で40%です。スーパーボール級をうろついての勝率として低いですが、極端に勝てなかったというわけでもなさそうです。(仮に勝率が5%を割ったら分析モデルを作って対戦結果を予測しても、適当に敗北といってれば95%の精度を誇ることになってしまいます)。
手元にあるデータがどういうものか確認したので、データのどの部分を採用するか考えます。全てを採用するよりノイズになりそうな変数を除外する方が核心をついた分析になるためです。ただその前にそのままでは使えない変数を調整します。
3-4. 変数の一部をダミー変数にする
データには下記のカテゴリカルな変数があります。カテゴリカルとは性別や血液型など数値では一概に表せないもののことです。
- 自分のダイマックスポケモン
- 自分の初手選出ポケモン
- 相手のダイマックスポケモン
- 相手の初手選出ポケモン
これらはポケモンの名前という量的でない値が入っているので、そのままでは計算に使うことができません。(この辺は分析手法によります)。
そこで、このカテゴリカルな変数を0または1のフラグを持つ形式に変換したいと思います。
変換後は自分のダイマックスポケモンであれば「カプ・レヒレ_ダイマックスフラグ」、「コジョンド_ダイマックスフラグ」のように複数の変数として分かたれ、値は1と0のフラグで格納されます。これをダミー変数といいます。
battle_results = pandas.get_dummies(battle_results)
これで全ての変数が数値として利用できるようになりました。なので話を戻して、どれを説明変数として採用するか考えていきます。
3-5. 説明変数を選定する
まず3-3の流れで決まったドラピオン、ストリンダー、オンバーン、コジョンドの4匹と関わる全ての変数の除外です。選出フラグと、ダミー変数化したダイマックスフラグと初手選出フラグです。
また32の値しかないシーズン、6と7しかなく大して差がない相手のランクも除外します。
残る変数の内、最初にムゲンダイナとカプ・レヒレについて考えていきます。
この二匹の戦績について深堀してみると下記のような結果を得られました。
| カプ・レヒレのダイマックス数 | ダイマックス時の勝率 |
|---|---|
| 20 | 30% |
カプ・レヒレがダイマックスした時の勝率が他に比べて低くなってました。ムゲンダイナ、カプ・レヒレ、ダイマックスフラグ、初手選出フラグの組み合わせの中で勝率が30%以下なのはここだけでした。これは金脈を見つけたかもしれません。
最後に残ったのは相手の繰り出してきたポケモンごとのダイマックスフラグ、初手選出フラグ、禁伝の選出数、ザシアン選出フラグです。
これらの変数、相手にまつわるものとしてグループ化できそうですが、ここで気になるのは多重共線性の問題です。
多重共線性とは例えば血液型それぞれのフラグ変数がある時、AB型フラグが1なら他は必ず0、他のどれかが1なら0になりますが、この一方の値によって、もう一方の値がある程度決まってしまう問題のことです。これをやってしまうと説明変数間の相関によって分析結果が歪んでしまうので警戒する必要があります。
となると相手にまつわる変数の中から代表を見繕うのが良さそうです。禁伝の選出数なら、ザシアン選出フラグ、相手のダイマックスポケモン、相手の初手選出ポケモンを包括していそうです。実際のところ、相手のダイマックスポケモンと初手選出ポケモンについては十分な数遭遇した個体がいなかったので選択の余地がありませんでした。
というわけでカプ・レヒレのダイマックスと禁伝の選出数に絞って分析を行います。この二つについては特に標準化の必要もなく、そのまま分析をしてよさそうです。手法はロジスティック回帰分析とします。
ロジスティック回帰分析を採用したのは、比較的とっつきやすく、何より実装しやすいからです。この手法は説明変数からデータがどのクラスに属するかを予測するもので、今回であれば目的変数を勝ったか負けたかに設定して識別するモデルを作成できます。
3-6. ロジスティック回帰分析
データから学習用と検証用のデータを取得します。
# データの内80%を学習用、残り20%を検証用にする。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state = 0, shuffle = True, test_size = 0.2)
次にモデルを作成します。公式リファレンスによると、もっと色々な引数を指定できるようですが、よく分からないまま増やしても歪みにしかならないので、最低限だけパラメーターを設定して後はデフォルトに任せます。
# ロジスティック回帰モデルを作成する。
lr = LogisticRegression(C = 1.0, penalty = 'l2', solver = 'lbfgs')
# 学習させる。
lr.fit(X_train, Y_train)
各パラメーターの意味ですが概ね下記のようなイメージだと考えています。
- C => 正則化の強さ。値が小さいほど強さが増す。
- penalty => 「L1正則化」か「L2正則化」を渡す。その目的はパラメーターにペナルティを科すことで過学習の対策をすることです。過学習とはサンプルデータにだけ強いモデルを作ってしまうことと言えます。「l1正則化」は余分なパラメーターを0にする性質があり、今回は事前に説明変数から関係なさそうなものを捨てたので採用しませんでした。ちなみに機械学習では基本的にl2を採用することが多いそうです。
- solver => 機械学習アルゴリズムの挙動を設定する探索アルゴリズム。定数とかではなく文字列を渡すのがpythonらしいです。
上記のパラメーターとデータによってポケモン対戦のモデルを作成することができました。それではいざ説明変数の詳細を追っていきましょう!。
3-7. 説明変数の係数を出力する
モデルの説明変数の係数はcoef_に格納されるので出力してみます。
lr_coefficients = pandas.DataFrame(index = X.columns)
lr_coefficients['coefficient'] = lr.coef_[0]
print(lr_coefficients.sort_values('coefficient', ascending = False))
| coefficient | |
|---|---|
| 相手の禁伝の選出数 | -0.328337 |
| カプ・レヒレのダイマフラグ | -0.362559 |
どちらもチームの勝利に負の影響を与えていました。ごめんよレヒレ。。。
相手の禁伝の選出数についてはステータスからして一般ポケモンとは違うので、さもありなんです。当たり前の結果ではありますが考えてみると意外と妥当なモデルを作れたということなのかもしれません。
このモデルがどれくらい正確なのかについて次に考えていきます。
3-8. モデルの性能を評価する。
混同行列、正解率、適合率、再現率、F1スコアと指標は色々ありますが、UndefinedMetricWarningが止まらなかったのでカットしてROC曲線のみを求めます。
ROC曲線とはモデルの分類性能を示す曲線で、横軸に偽陽性率、縦軸に真陽性率をとります。(サンプル数が少ないと曲線ではなくなります)。
各点は閾値ごとに偽陽性率と真陽性率がどのように現れるかを表現しますが、閾値自体はグラフで見れないのがポイントです。
例えば閾値が1.0の場合、基準が高すぎて全てが陽性グループから弾かれるので原点に点が打たれます。逆の場合は確実に陽性になるのでグラフの最も右上に点が打たれます。
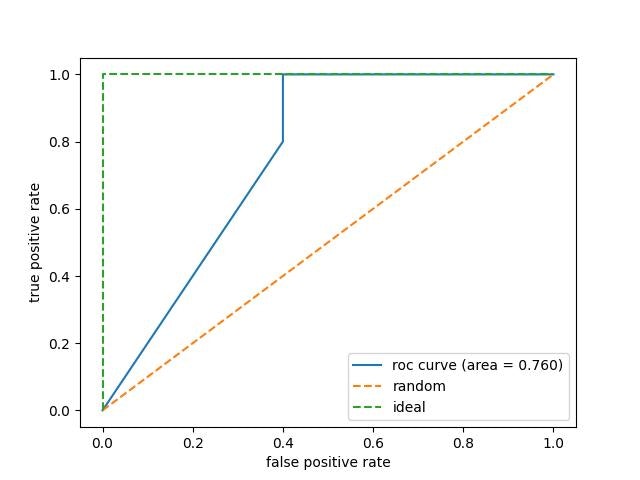
下記に、比較用にランダムに推測した場合の線と理想線を併せて作図したものを貼っておきます。
このROC曲線のどこを見ればいいかですが線の下側の面積であるAUCです。最大値は1で1に近いほど性能が高く最悪なのは0.5です。1は緑色の理想線で、0.5はオレンジ色のランダム線です。0.5の場合適当に予測するのと同じになります。予断ですが0.5を下回る場合はよく外れる占いはよく当たるという話になり、真の条件を反転させた方がいいという展開になります。
作成したモデルのaucは0.76で高いともいえない分類性能でした。もう少しだけ上を目指したいのでパラメーターの調整に入ります。
3-9. optunaでパラメーターのチューニングをする
optunaを使いロジスティック回帰分析のトライアルを繰り返し行うことで、より良いパラメーターを探っていきます。数打てば当たるを力技で進めていくイメージですね。評価の基準は正解率とし60秒間実行します。
def logistic_regression_analysis_trial(trial):
# ハイパーパラメータを設定する。
params = {
'C' : trial.suggest_loguniform('C', 0.0001, 10),
'penalty' : 'l2',
'solver' : trial.suggest_categorical('solver', ['lbfgs', 'liblinear'])
}
lr = LogisticRegression(**params)
# 評価指標として正解率を指定する。
scores = cross_validate(lr, n_jobs = -1, scoring = 'accuracy', X = X_train, y = Y_train)
return scores['test_score'].mean()
optuna.logging.set_verbosity(optuna.logging.WARN)
study = optuna.create_study(direction = 'maximize')
study.optimize(logistic_regression_analysis_trial, callbacks=[logging_callback], timeout = 60)
またデフォルトでは試行の記録が順次吐かれていきますが、高速で大量にスクロールされたところで追えないため、最高記録を塗り替えた時だけログを出力するようカスタマイズします。ほとんど公式リファレンスのコピペです。
def logging_callback(study, frozen_trial):
previous_best_value = study.user_attrs.get('previous_best_value', None)
if previous_best_value != study.best_value:
study.set_user_attr('previous_best_value', study.best_value)
print(
"Trial {} finished with best value: {} and parameters: {}. ".format(
frozen_trial.number,
frozen_trial.value,
frozen_trial.params,
)
)
結果は下記のようになりました。
C = 0.00014182172596081152,
penalty = 'l2',
solver = 'lbfgs'
3-10. ロジスティック回帰分析のモデルを作り直す
それではチューニングしたパラメーターを用いて、もう一度分析をやり直してみます。
lr2 = LogisticRegression(
C = 0.00014182172596081152,
penalty = 'l2',
solver = 'lbfgs'
)
lr2.fit(X_train, Y_train)
lr2_Y_pred = lr2.predict(X_test)
lr2_Y_pred_proba = lr2.predict_proba(X_test)
lr2_fpr, lr2_tpr, lr2_thresholds = roc_curve(y_true = Y_test, y_score = lr2_Y_pred_proba[:, 1])
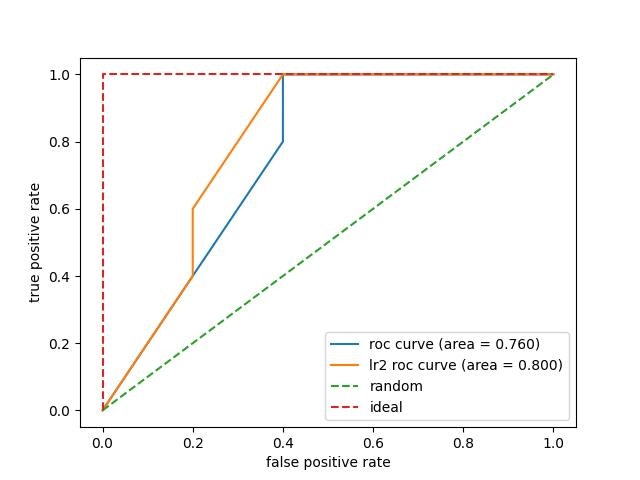
matplotlib.pyplot.plot(lr2_fpr, lr2_tpr, label='lr2 roc curve (area = %0.3f)' % auc(lr2_fpr, lr2_tpr))
結果AUCが80%を超えました! 前回よりもいい数字です。
係数を出力したところ、値は小さくなりましたが同じような結果を得られました。
| coefficient | |
|---|---|
| 相手の禁伝の選出数 | -0.000301 |
| レヒレダイマフラグ | -0.000195 |
3-11. K分割交差検証
駄目押しの検証で5分割交差検証を行います。教師データとテストデータの採り方を変えることで、本当に一般的なモデルを作れたのか? このサンプルデータの狭い世界でのみ通用する法則ではないか? といったことを調べていきます。指標を正解率に設定し、比較用に旧モデルと併せて検証をします。
lr_scores = cross_val_score(lr, X_train, Y_train, cv = 5, scoring = 'accuracy')
print(lr_scores)
# [0.375 0.625 0.625 0.625 0.625]
lr2_scores = cross_val_score(lr2, X_train, Y_train, cv = 5, scoring = 'accuracy')
print(lr2_scores)
# [0.625 0.625 0.625 0.625 0.625]
結果は全て0.625で、少なくともテストデータの採り方によって大きなズレが生じることはないようです。ここでも改良後のモデルは最初のモデルよりいい結果を出しましたが、0.625という数値自体は微妙でした。あれこれ手を尽くそうと思えばできますが、そこまでしても元々のデータが完全といえないので、ここで区切りとします。
※ 今回は検索して情報の多いcross_val_scoreを使いましたがAPIとしては下記の方が新しいです。
cross_validate(lr2, X_train, Y_train, cv = 5, scoring = ['accuracy', 'f1'])
4. まとめ
今回の目的はポケモンの対戦結果の特徴を割り出し改善案に昇華するというものでした。そして得られたのは勝利への道筋ではなく、どういう展開で敗北しているかの要因でした。
「カプ・レヒレのダイマックス」が負の要因として出てきてしまったのは痛恨で、思い当たる節がないでもありません。私がレヒレをダイマックスさせるのは、でもしかダイマックスのパターンが多く、敗色濃厚だけど諦めきれないし、とりあえず硬いレヒレで凌ぐかみたいなのが多かった気がします。
あんなに強いレヒレに不名誉なことをしてしまったので、次回はレヒレを研究してパーティの負け筋の回避と勝ち筋の策定を同時に達成したいところですが、9月からのシーズンが幻のポケモンの解禁で無法地帯と化してしまうので難しいかもしれません。
その時はスカーレットバイオレットの発売を待って、そこから再開しようかなー、と考えてます。スカバイを買ったらきっと沢山対戦するのでサンプルデータももっと揃えたいです。
以上です。ここまで読んでくれてありがとうございました。
もしよければ感想など教えてください。