Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@mimitaro

ポケモンで学ぶRによる統計

Posted at

はじめに

最近統計を勉強しているのですが、ポケモンのデータを使って遊んでみようと思いました。
今回はRを使って、ポケモンのデータを解析してみます。
後半になるにつれ、良いデータが取れず、歯切れの悪い説明となったのが反省点です。

ポケモンのデータ

ポケモンのデータはポケモン徹底攻略様から取得しました。
同サイトのポケモン図鑑から、データを色々と工夫して拝借し、csvとしてまとめました。

今回はポケットモンスターソードシールドに登場するポケモンのみを対象にしています。
またポケモンには同名であってもフォームが異なるものがいますが、ポケモン徹底攻略様のポケモン図鑑に準じて、種族値(基本ステータスのようなもの)が異なる場合は別ポケモンとみなします。

具体的には、地方毎のフォームを持つポケモン(ニャース、ライチュウなど)、オスとメスで種族値や覚える技が違うポケモン(ニャオニクス、イエッサン)、複数の姿を持つポケモン(ロトム、ウーラオス)はそれぞれの姿を別ポケモンとカウントします。

結果、734行分のデータがあつまりました。

また今回取得する情報は以下の通りです。

  • 全国図鑑におけるNo
  • ポケモンの名前
  • ポケモンの第1タイプ
  • ポケモンの第2タイプ
  • 身長(m)
  • 体重(kg)
  • HP種族値
  • こうげき種族値
  • ぼうぎょ種族値
  • とくこう種族値
  • とくぼう種族値
  • すばやさ種族値
  • カテゴリー(通常、準伝説、伝説、幻)
  • すがた

例えばフシギダネ、ライチュウ、ミュウツーは以下のようになります。

No なまえ タイプ1 タイプ2 身長 体重 HP こうげき ぼうぎょ とくこう とくぼう すばやさ カテゴリー すがた
1 フシギダネ くさ どく 0.7 6.9 45 49 49 65 65 45 通常ポケモン
26 ライチュウ でんき エスパー 0.7 21.0 60 85 50 95 85 110 通常ポケモン アローラのすがた
26 ライチュウ でんき 0.8 30.0 60 90 55 90 80 110 通常ポケモン
150 ミュウツー エスパー 2.0 122.0 106 110 90 154 90 130 伝説のポケモン

前述した通り、同じ全国図鑑Noであってもライチュウは2つの姿が存在するため、2匹分となります。

image0.jpeg

Rでの共通部分

今回は元となるポケモン図鑑のデータをpokedex.csvというファイルでまとめています。
そのため、これから紹介するRのソースコードは以下の記述を共通して持っています。

共通部分のcsv読み込み
# ------------------------------
# ポケモン図鑑のCSv読み込み
# ------------------------------
pokedex <- read.csv("pokedex.csv", fileEncoding = "sjis")

またRStudioを使っているため、事前にメニューバーの「Session」→「Set Working Directory」→「Choose Directory」から該当のcsvがあるディレクトリを選択しておきます。
この操作は内部的にはsetwd()関数と同じで、作業先のディレクトリを変更しています。

ヒストグラム

ヒストグラムとは特定区間の量をグラフでまとめたものです。例えば月ごとの売上総数、都道府県ごとの人口など、様々な区分におけるデータ量を可視化して比較できます。

今回はポケモンの身長のヒストグラムを求めてみます。
Rのヒストグラムを描画する関数hist()は、デフォルトでスタージェスの公式に基づいて幅を決めます。
今回は手動で決めたいので、目安のためにポケモンの身長の最大値と最小値をまず求めます。

ポケモンの身長の最大と最小を求める
# ポケモンの身長の最大と最小を求める
poke_height = pokedex$height
poke_max_height = poke_height[which.max(poke_height)]
poke_min_height = poke_height[which.min(poke_height)]
print(poke_max_height)
print(poke_min_height)
ポケモンの身長の最大と最小を求める(結果)
[1] 100
[1] 0.1

結果は最小値が0.1mで、最大値が100mです。そのため幅を10mとすると以下のように記述できます。

ポケモンの身長のヒストグラム描画
# ------------------------------
# ポケモンの身長のヒストグラム
# ------------------------------
# ポケモン図鑑から身長を取り出す
poke_height = pokedex$height

# ポケモンの身長ヒストグラム描画
hist(poke_height,
     breaks = seq(0, 100, 10),
     main = "ポケモンの身長のヒストグラム",
     xlab = "ポケモンの身長",
     col = "Green")

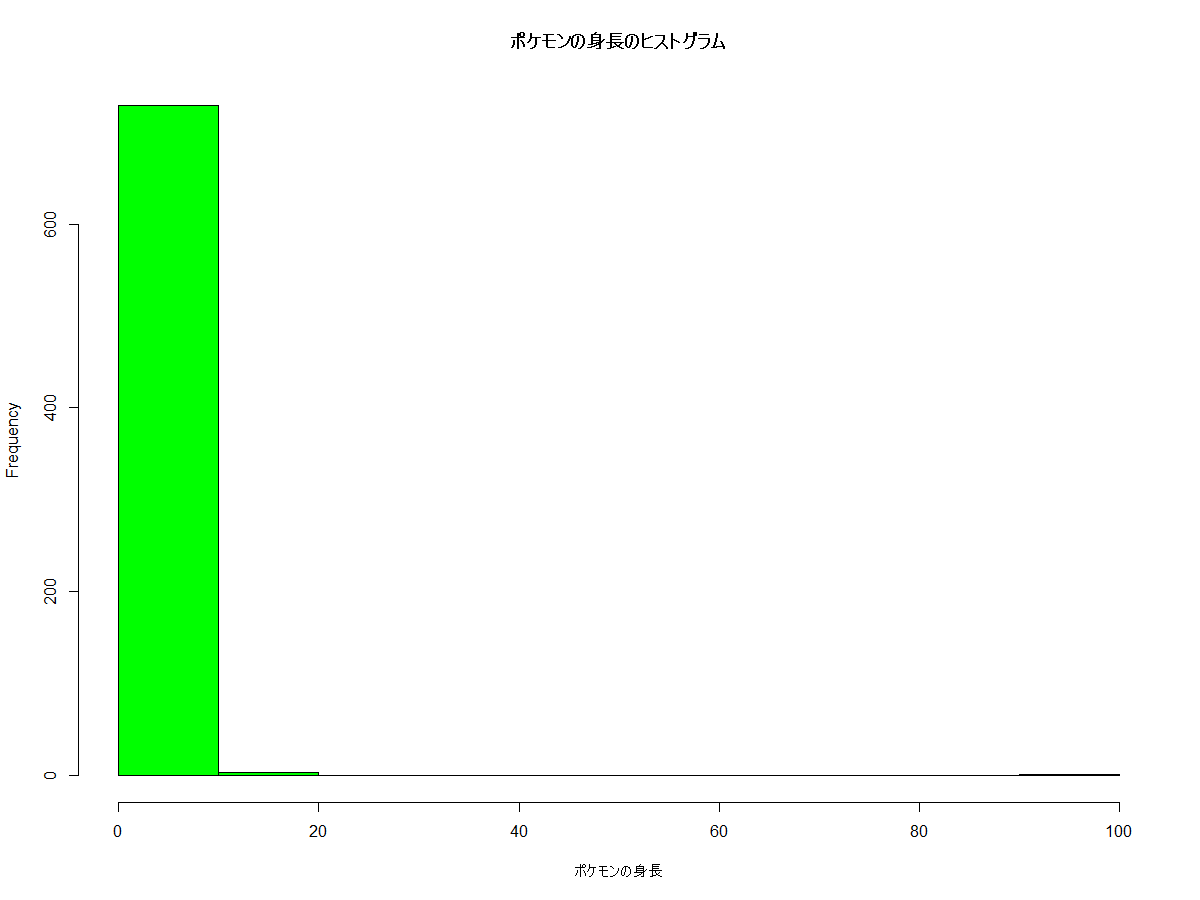
これにより得られるヒストグラムは以下の通りです。

pokemon_hist_01.png

大半のポケモンが10m以下であることは分かりますが、それ以外のことは殆ど分かりません。
よく見ると、100mの値は外れ値になっています。外れ値とは他のデータと比較して極端な値を指します。
この外れ値を含めて区分を考えたため、適切ではないヒストグラムになってしまいました。

よって外れ値である100mのポケモンを省いた上で、区分を考えヒストグラムを作り直します。
そのために2番めに大きいポケモンの身長を求めます。

2番めに大きいポケモンの身長を求める
# 2番目に大きい身長を求める
poke_2nd_height = sort(poke_height, decreasing= T)[2]
print(poke_2nd_height)
2番めに大きいポケモンの身長を求める(結果)
[1] 20

これにより20mであるこが分かりました。

ついでにあまり意味はないですが、100.0mのポケモンの名前と姿がなにであるか確かめます。

身長が最大のポケモンを調べる
# 身長が最大のポケモンの名前と姿名を表示
h_max_no = which.max(poke_height)
print(pokedex$name[h_max_no])
print(pokedex$form[h_max_no])
身長が最大のポケモンを調べる(結果)
[1] "ムゲンダイナ"
[1] "ムゲンダイマックス"

するとムゲンダイナ(ムゲンダイマックスのすがた)であることが分かります。これはストーリー上のみで戦える巨大な伝説のポケモンです。

image1.jpeg

外れ値を省くため以下のように描画範囲を0～20mの範囲にし、幅を0.5mにします。
今回は描画範囲を0～20mに限定することで、ヒストグラムから外れ値を省いています。
他にもpoke_height[poke_height < 200]と記述することで、200m未満の身長を抽出することができます。

ポケモンの身長のヒストグラム描画(外れ値除外)
# ------------------------------
# ポケモンの身長のヒストグラム
# ------------------------------
# ポケモン図鑑から身長を取り出す
poke_height = pokedex$height

# ポケモンの身長ヒストグラム描画
hist(poke_height,
     breaks = seq(0, 100, 0.5),
     xlim = c(0, 20),
     xaxp = c(0, 20, 20), 
     main = "ポケモンの身長のヒストグラム",
     xlab = "ポケモンの身長",
     col = "Green")

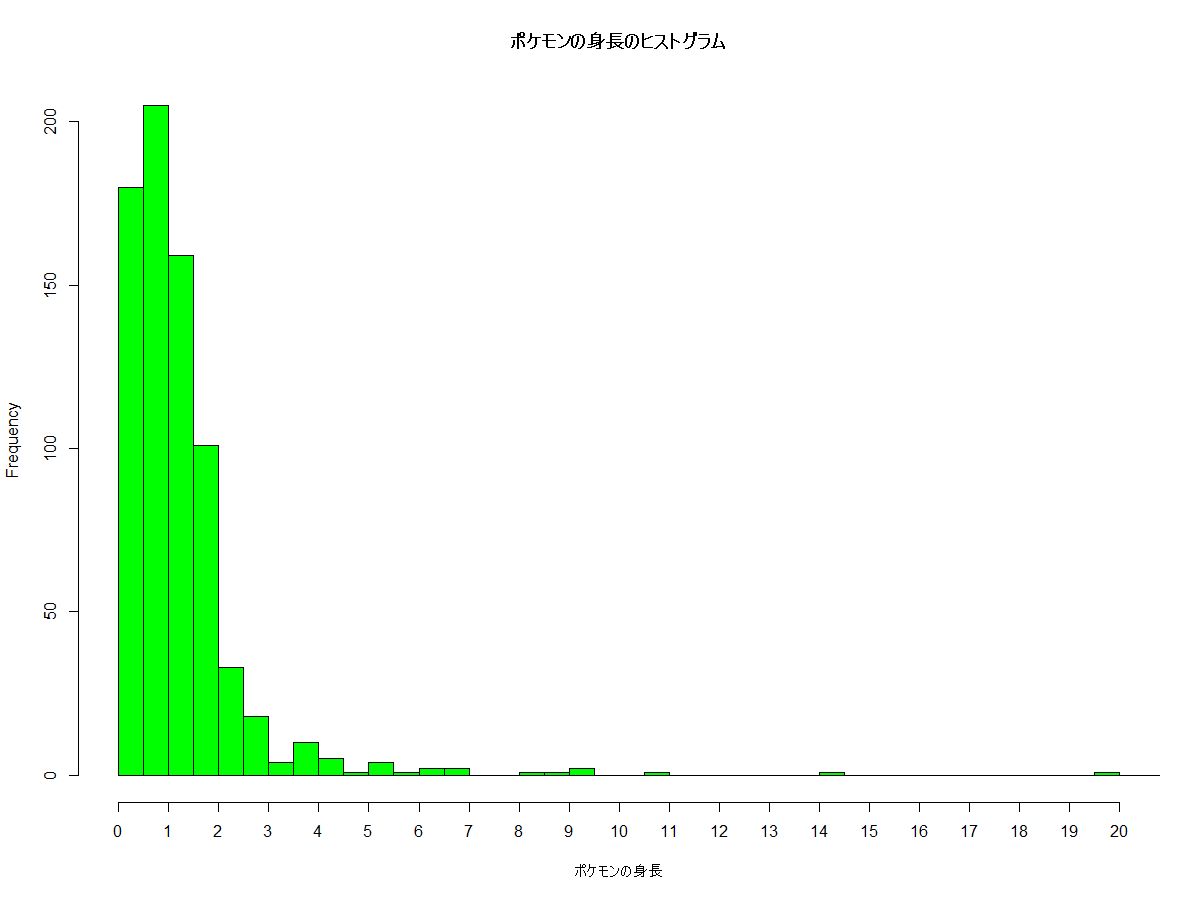
この結果が次のヒストグラムです。

pokemon_hist_02.png

見ての通り、ポケモンの身長は2m以下に集約していることが分かります。"ポケット"モンスターなだけはあり、子供より小さい1m以下が非常に多くいます。
逆に巨大怪獣のように大きいポケモンは殆どいないことが分かります。

箱ひげ図

箱ひげ図とは最大値、最小値、中央値を1つのグラフで表すことで、データのばらつきを分かりやすく可視化したものです。

今回はポケモンの各種族値を箱ひげ図で表してみます。種族値とはポケモンのステータスの基本となる値であり、例えばピカチュウならすばやい、カイリキーなら力が強い、などを表す値です。
ただしポケモンごとに種族値はバラけていることは明白なため、今回は伝説のポケモン(準伝説含む)の種族値で箱ひげ図を作ります。

image3.jpeg

伝説のポケモンとは、フリーザー、ミュウツー、ホウオウなどであり、どれも高いステータスを誇っています。
そのため、伝説のポケモンが本当に種族値が高い範囲でまとまっているのかを箱ひげ図から分析します。

伝説のポケモンによる種族値箱のひげ図
# ------------------------------
# ポケモンの種族値の箱ひげ図(伝説のポケモンのみ)
# ------------------------------
# 伝説のポケモンの種族値取得
poke_hp = pokedex$hp[pokedex$category != '通常ポケモン']
poke_atk = pokedex$atk[pokedex$category != '通常ポケモン']
poke_def = pokedex$def[pokedex$category != '通常ポケモン']
poke_spatk = pokedex$spatk[pokedex$category != '通常ポケモン']
poke_spdef = pokedex$spdef[pokedex$category != '通常ポケモン']
poke_spd = pokedex$spd[pokedex$category != '通常ポケモン']

# 伝説のポケモンの種族値箱ひげ図を描画
boxplot(list(HP=poke_hp,
             こうげき=poke_atk,
             ぼうぎょ=poke_def,
             とくこう=poke_spatk,
             とくぼう=poke_spdef,
             すばやさ=poke_spd),
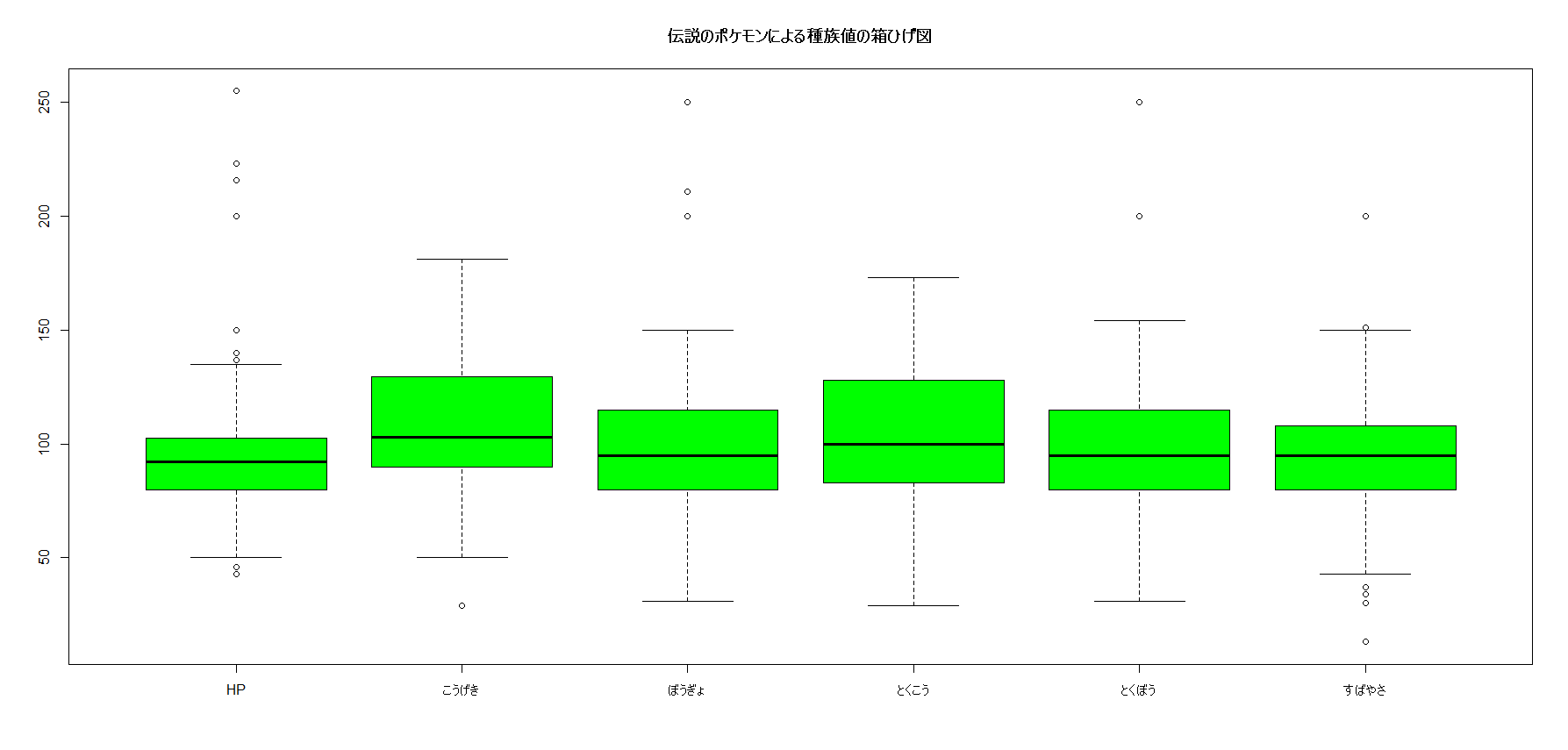
        main = "伝説のポケモンによる種族値の箱ひげ図",
        col = "green"
        )

pokemon_hist_03.png

基本的にポケモンの種族値は100を超えていれば十分、120以上ならば高いと言えます。
伝説のポケモンだけはあり、殆どの種族値の中央値が100付近です。

単回帰分析

単回帰分析とはある1つの要因(説明変数)から、何かを予測(目的変数)することです。
例えば日々の気温(説明変数)と自販機の売上(目的変数)の関係を調べ、気温が高いほど自販機の売上は上がること、また気温によって自販機の売上はどの程度であるかを予測することができます。
ちなみに説明変数を複数(2つ以上)用いて、目的変数を予測することを、重回帰分析といいます。

今回はポケモンの身長(説明変数)とHP種族値(目的変数)の単回帰分析を行います。例えば小さいことで有名なバチュル(0.1m)はHP種族値が50しかありません。一方、大きいことで有名なホエルオー(14.5m)はHP種族値が170もあります。

image2.jpeg

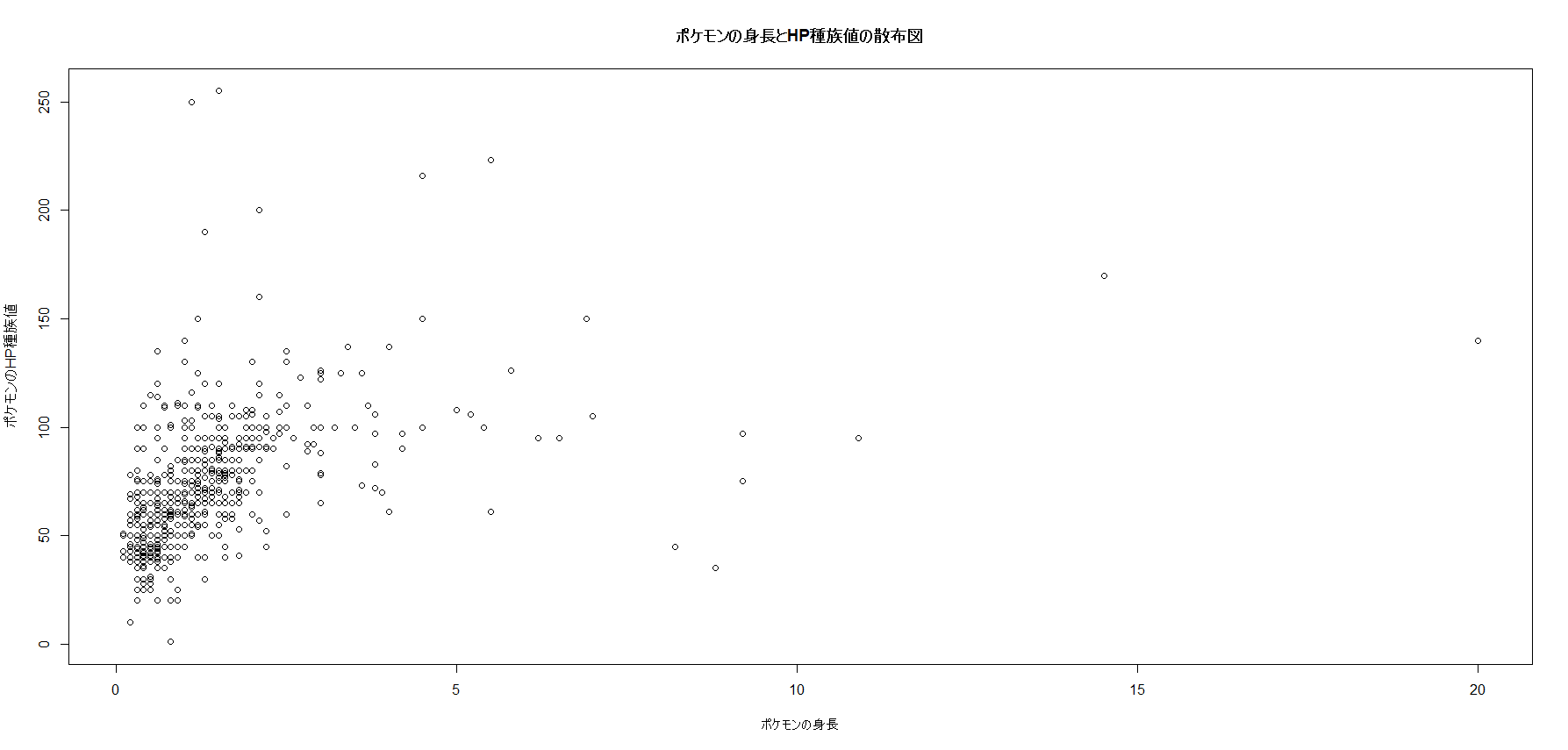
まずポケモンの身長とHP種族値の散布図を見ます。

ポケモンの身長とHP種族値の散布図
# ポケモンの身長とHP種族値(ムゲンダイマックスしたムゲンダイナを除く)
poke_height = pokedex$height[pokedex$height < 100]
poke_hp = pokedex$hp[pokedex$height < 100]

# 散布図の描画
plot(poke_height, poke_hp,
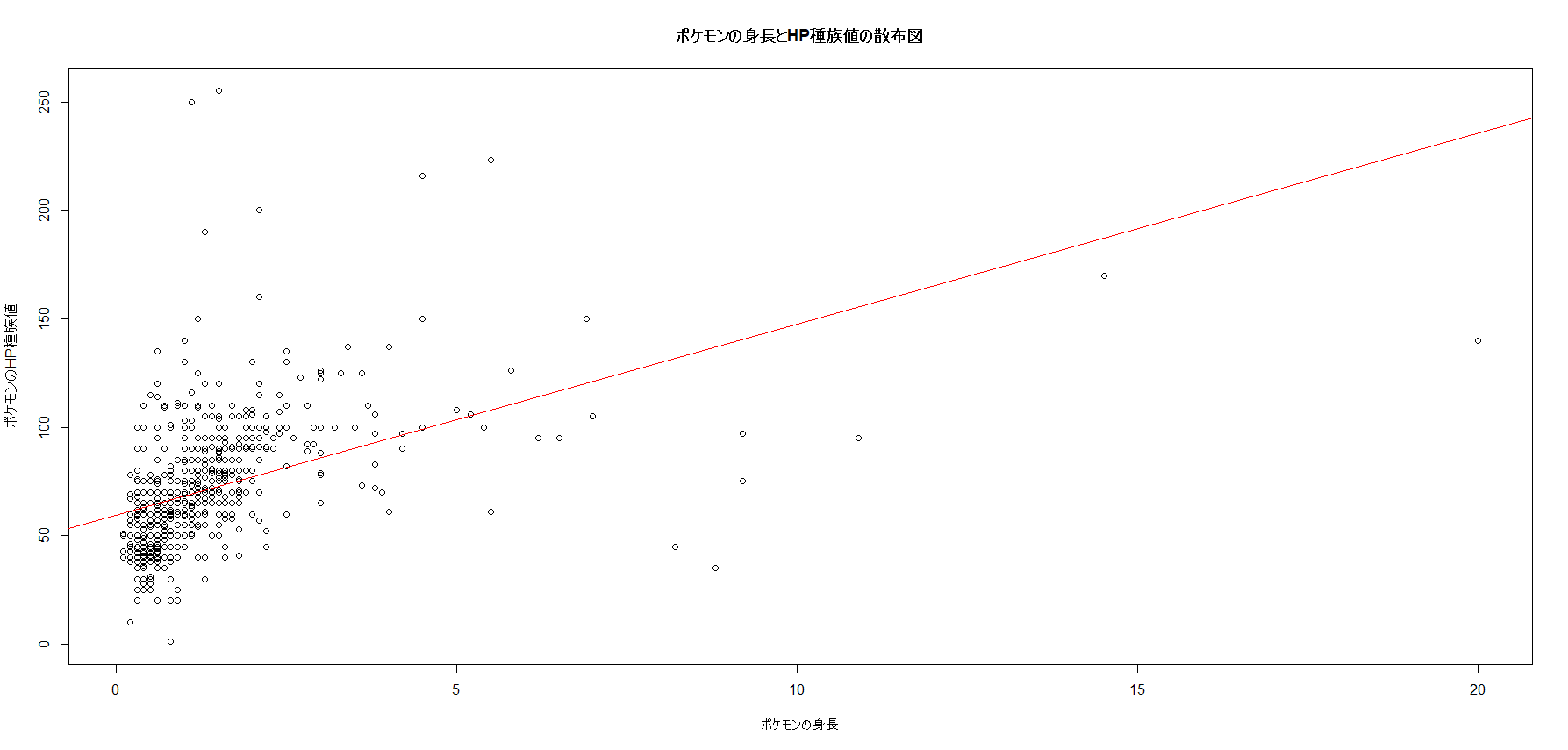
     main = "ポケモンの身長とHP種族値の散布図",
     xlab = "ポケモンの身長",
     ylab = "ポケモンのHP種族値")

pokemon_hist_04.png

外れ値もありますが、概ね身長が高いほどHP種族値が大きいことが分かります。
では実際に身長(説明変数)からHP種族値(目的変数)を予測するために、回帰分析を行い予測の式である回帰式を求めます。

ポケモンの身長とHP種族値の単回帰分析
# ------------------------------
# ポケモンの身長とHP種族値の単回帰分析
# ------------------------------
# ポケモンの身長とHP種族値(ムゲンダイマックスしたムゲンダイナを除く)
poke_height = pokedex$height[pokedex$height < 100]
poke_hp = pokedex$hp[pokedex$height < 100]

# 散布図の描画
plot(poke_height, poke_hp,
     main = "ポケモンの身長とHP種族値の散布図",
     xlab = "ポケモンの身長",
     ylab = "ポケモンのHP種族値")

# 最小二乗法による単回帰分析
result <- lm(poke_hp ~ poke_height)
# 結果表示
summary(result)

# 結果の描画
abline(result,
       col = "Red")
ポケモンの身長とHP種族値の単回帰分析(結果)
# 最小二乗法による単回帰分析
Call:
lm(formula = poke_hp ~ poke_height)

Residuals:
     Min       1Q   Median       3Q      Max 
-102.016  -14.864   -2.233   12.060  182.280 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  59.5083     1.2508   47.58   <2e-16 ***
poke_height   8.8077     0.6444   13.67   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 25.07 on 730 degrees of freedom
Multiple R-squared:  0.2038,	Adjusted R-squared:  0.2027 
F-statistic: 186.8 on 1 and 730 DF,  p-value: < 2.2e-16

結果から回帰式「HP種族値 = 59.5083 + 8.8077 × ポケモンの身長」が求まります。
この回帰式を先程の散布図に描画すると以下の赤い線となります。

pokemon_hist_05.png

この回帰式がどの程度正しいと言えるか(=有意がある)は、p値から分かります。
p値は乱暴に言えば「ポケモンの身長とHP種族値が無関係のとき、たまたま関係があるように見える確率」です。
p値についての解説は非常に長くなるため参考リンク先を参照してください。

上記結果のPr(>|t|)がp値であり、一般的な有意水準5%(有意水準)より小さいため、有意があると言えます。
そのためポケモンの身長が高いほどHP種族値が高くなる傾向があると言えます。

では実際に、回帰分析に使われていないポケモンを使って、予測の精度をテストしてみます。
前述した通り、今回はポケットモンスターソードシールドに出現するポケモンのみをサンプルとしています。
ソードシールドに出現しないポケモンたちで予測をテストした結果は以下の通りです。

なまえ 身長 回帰式で予測したHP種族値 実際のHP種族値
スピアー 1.0m 68.316 65
モココ 0.8m 66.55446 70
マルノーム 1.7m 74.48139 100
ゴウカザル 1.2m 70.07754 76
クルマユ 0.5m 63.91215 55
ゲッコウガ 1.5m 72.71985 72
ケララッパ 0.6m 64.79292 55

適当に選びましたが、小さいこ(クルマユ、ケララッパ)や大きいこ(マルノーム)以外はそれなりに当たっています。
これは散布図を見るに、約1mのサイズの場合、精度が高いからと思われます。

先程のR結果を見てみると、Multiple R-squaredの値が0.2038しかありません。
これは決定係数と呼ばれる値で、説明変数(ポケモンの身長)がどの程度、目的変数(ポケモンのHP種族値)を説明しているかの指標です。

先程のp値は、「ポケモンの身長」は「ポケモンのHP種族値」に影響を与えている、ことを示しています。

対して決定係数は、「ポケモンの身長」により予測値が、実際の「ポケモンのHP種族値」をどの程度あてはまるかを、示しています。

ポケモンの身長が高いほど、HP種族値も高くなることは散布図からも納得はできます。
しかしそこから求めた予測値は、あまり高くないと言えます。

主成分分析

主成分分析とは、複数ある変数から新たな軸を作ることで、未知なるデータの構造への理解を深める手法です。

今回はポケモンの6つの種族値(HP、こうげき、ぼうぎょ、とくこう、とくぼう、すばやさ)を使って主成分分析を実行します。
結果を描画するだけの場合、「biplot(poke_pca)」とすれば、一瞬で結果が出るので楽です。
今回は、散布図において通常ポケモンを緑、伝説のポケモン等を赤で表したいため、独自に描画させます。

ポケモンの種族値の主成分分析
# ------------------------------
# ポケモンの種族値の主成分分析
# ------------------------------
# ポケモンの種族値
x <- pokedex[, 7:12]

# 主成分分析
poke_pca <- prcomp(x, scale. = TRUE)

# 結果表示
summary(poke_pca)

## 結果描画
# 各主成分の固有ベクトル
poke_pca_rota <- poke_pca$rotation

# 通常ポケモンとそれ以外(伝説のポケモン等)で色分け
poke_cols <- character(nrow(x))
poke_cols[pokedex$category == '通常ポケモン'] <- 'green'
poke_cols[pokedex$category != '通常ポケモン'] <- 'red'

# 散布図
plot(poke_pca$x[,c(1,2)],
     col=poke_cols,
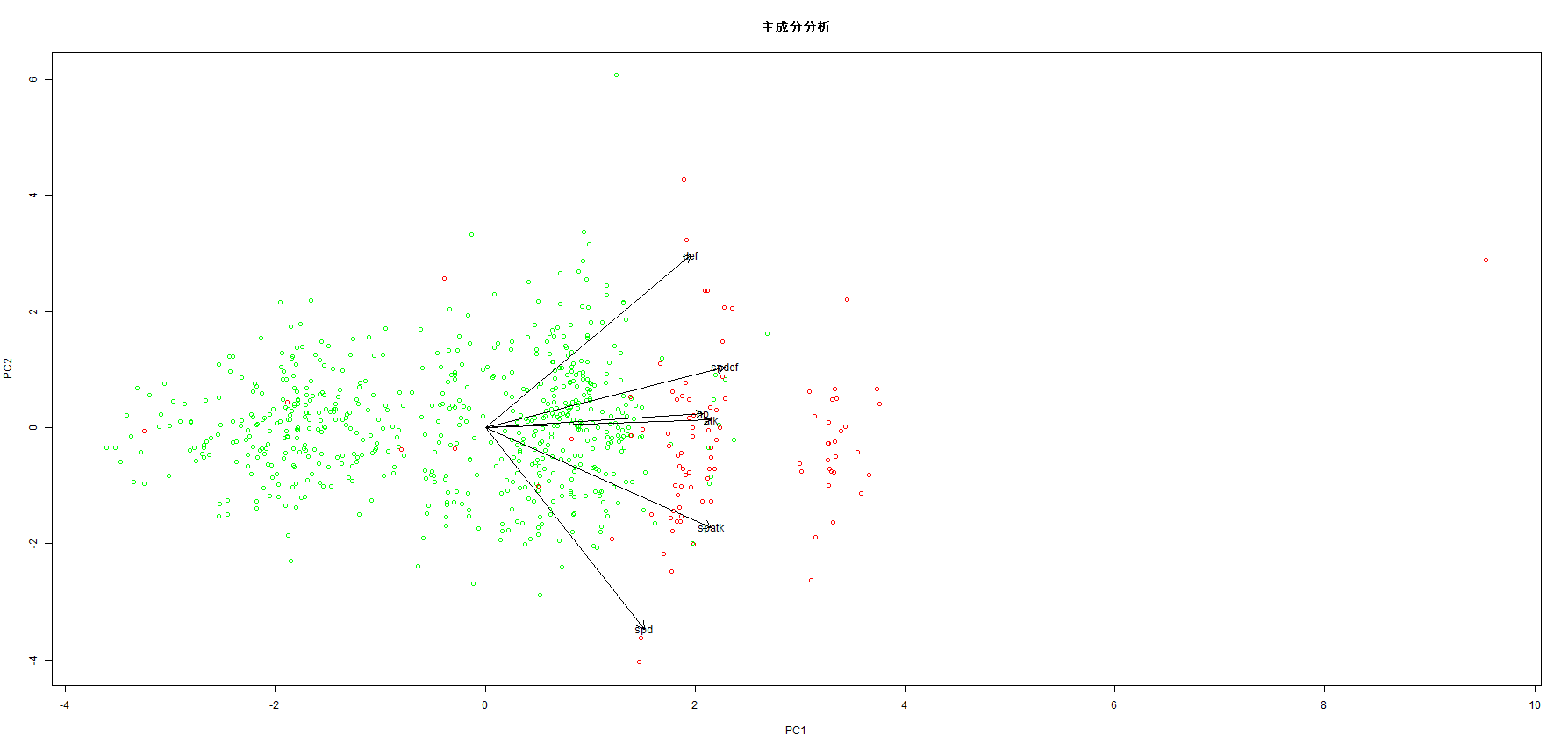
     main='主成分分析')

# 変数の矢印 (見やすくするため矢印の長さを5倍にする)
arrows_end_1 = poke_pca_rota[,1]*5
arrows_end_2 = poke_pca_rota[,2]*5
arrows(0, 0, arrows_end_1, arrows_end_2, length = 0.1)

# 変数名表示
text(arrows_end_1, arrows_end_2, labels=rownames(poke_pca_rota))
ポケモンの種族値の主成分分析(結果)
Importance of components:
                          PC1    PC2    PC3    PC4     PC5     PC6
Standard deviation     1.6178 1.0594 0.9307 0.8380 0.65837 0.50837
Proportion of Variance 0.4362 0.1870 0.1444 0.1170 0.07224 0.04307
Cumulative Proportion  0.4362 0.6233 0.7677 0.8847 0.95693 1.00000

pokemon_06.png

第1主成分は正の方向であるほど全種族値は高くなります。
少し強引ですが、ポケモンのステータス合計の高さを示していると解釈できます。
第2主成分は、正の方向の場合、とくぼうとぼうぎょが高く、負の方向の場合、とくこうとすばやさが高いです。
こちらも少し無理がありますが、正の方向の場合は打たれ強く、負の方向の場合、脆いがすばやい、と解釈できそうです。

伝説のポケモンが、殆ど第1主成分が正の側にいる点から、伝説のポケモン=種族値が高いポケモン、と言えます。

image0.jpeg

ロジスティック回帰

ロジスティック回帰とは、確率を予測する手法です。
特に、好きか嫌いか、売れるか売れないか、持っているか持っていないか、など2値の事象に対して、どちらに属する可能性が高いかを予測します。
回帰分析では、種族値の値といった数字で表す量が予測できました。
一方、ロジスティック回帰では、あるカテゴリーに属する、属さない、などの質的データの予測に役立ちます。

今回は、ポケモンの合計種族値(説明変数)を使って、そのポケモンが伝説のポケモン(準伝説、伝説、幻)に属するかどうかを予測します。

ポケモンのロジスティック回帰
# ------------------------------
# ポケモンのロジスティック回帰
# ------------------------------
# 伝説のポケモン(=1)か否(=0)かをダミー変数で表す
poke_cate <- integer(nrow(pokedex))
poke_cate[pokedex$category == '通常ポケモン'] <- 0
poke_cate[pokedex$category != '通常ポケモン'] <- 1

# ポケモンの合計種族値
poke_base_st <- apply(pokedex[,7:12], 1, sum)

# ロジスティック回帰
result <- glm(poke_cate ~ poke_base_st, family = binomial, data = Default)

# 結果表示
summary(result)

# 結果描画
# ロジスティック回帰による予測
fit = fitted(result)
plot(poke_base_st, fit)
par(new=TRUE)
# 実際の値
# 確率が50%以上の場合は、伝説のポケモンと予測
# 予測結果が伝説の場合は赤、通常ポケモンの場合は緑で描画
cols <- integer(nrow(pokedex))
cols[fit>=0.5] <- 'red'
cols[fit<0.5] <- 'green'
plot(poke_base_st, poke_cate, col=cols)
ポケモンのロジスティック回帰(結果)
Call:
glm(formula = poke_cate ~ poke_base_st, family = binomial, data = Default)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.0636  -0.3074  -0.0600  -0.0065   5.3391  

Coefficients:
               Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -21.993486   2.096882  -10.49   <2e-16 ***
poke_base_st   0.038703   0.003839   10.08   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 598.67  on 732  degrees of freedom
Residual deviance: 251.34  on 731  degrees of freedom
AIC: 255.34

Number of Fisher Scoring iterations: 8

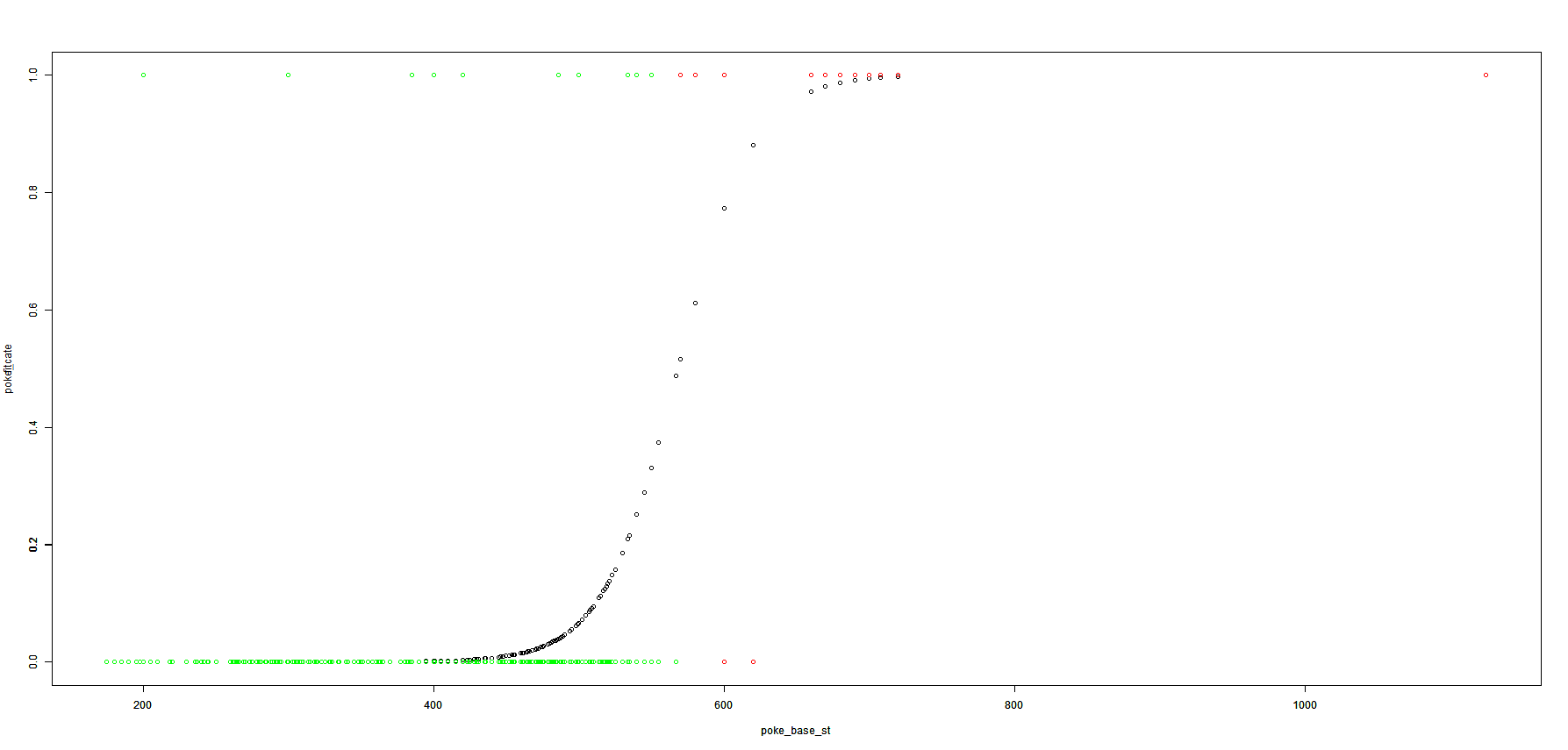
pokemon_07.png

上図では、伝説のポケモンの確率が50%以上の場合は、伝説のポケモンであると予測します。
そして予測結果が伝説のポケモンは赤、通常ポケモンの場合は緑で描画されます。
値0のラインでは多くのポケモンは通常ポケモンと予測されており、逆に値1のラインでは伝説のポケモンと予測されています。

参考リンク

R

回帰分析

主成分分析

ロジスティック回帰

  • 付録. M5実習5: ロジスティック回帰分析 - 統計ソフトRの使い方

    https://sites.google.com/site/webtextofr/seminar2

    Rによるロジスティック回帰の実行の仕方や結果の見方が載っています。
    ロジスティック回帰式の描画の参考にしました。
1
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?