GANのシンプルな理解と実装

GAN（Generative adversarial networks）（敵対的生成ネットワーク）を私なりになるべくシンプルに理解してなるべくシンプルに実装しました。

ニューラルネットワーク

ニューラルネットワークというものをご存じでしょうか。これは、あるベクトルを別のベクトルに変換するモデルです（本当はベクトルではなくテンソル）。そしてこれは学習することができ、学習が完了したニューラルネットワークは、入力したベクトルに対して適切なベクトルを出力することができるようになります。
例えば、「手書き数字の画像（各画素の濃淡の値を一列に並べたベクトル）を入力すると、何の数字か（0~9までの各値の確率を一列に並べたベクトル）が出力される」といった感じです。

画像生成

ニューラルネットワークは分類や回帰の問題を解くことが出来ますが、それ以外にも使い道はたくさんあります。ここで、以下の二点について考えてみましょう。

• ニューラルネットワークは、ベクトルが入力されると別のベクトルを出力する
• 画像はベクトルで表せる

こう見ると、ニューラルネットワークを使って画像を生成することができそうですね。出力されたベクトルを画像とみなせばいいのです。
入力には色々なものを想定できそうです。例えば入力に文章ベクトルを想定すれば文章から画像を生成するモデルになり、乱数を想定すればランダムな画像生成モデルになりますね。

敵対的学習

ニューラルネットワークを用いて画像が生成できることを示しましたが、学習が行われていないと、ただランダムな色が並んだだけの砂嵐のような画像が生成されるだけです。このように。

欲しい画像を生成できるようにするためには学習を行う必要があります。ではどうやって学習すればよいでしょうか。

通常のニューラルネットワークでは、入力とそれに対応する正解を用意して、出力が正解に近づくように=出力と正解の差が小さくなるように学習させます。これが画像生成モデルの学習にも使えればよいのですが、実は結構難しいのです。何が難しいかというと、正解となる画像を定めるのが難しいのです。

例えば、「魚が泳いでいる画像」が正解だとしましょう。ここで、以下の4枚の画像を見てください。

この4枚は全て正解になりますよね。このように、「これが正解！」というデータを一つに定めることが出来ないため、正解との差を小さくするような学習法が使えないのです。

では次にこんな方法を考えましょう。「画像の完成度を人間が判断する」というものです。この「完成度」は「偽物らしさ」とでも言い換えておきましょうか。用意した正解との差ではなく、人間が判断した「偽物らしさ」が小さくなるように学習させるということです。こうすれば、生成された画像の評価を人間の感覚に委ねるだけでよく、正解となるデータがいりません。しかし、これにも致命的な問題があります。それは微分ができないことです。ニューラルネットワークの学習とは、最小化したい値をパラメータで偏微分し、勾配を求め、値を小さくする方向にパラメータを更新することで適切なパラメータを得ることを指します。人間が偽物らしさを値として提示したところで、人間の思考を数式に起こすことが出来ず、微分のしようがないため、勾配を求められないのです。

いやー、惜しいですね。あと少しです。「偽物らしさ」を微分ができる形で出力できれば良いのですが...。さあ、ここで気づいた人もいるでしょう。そうです、画像の評価にもニューラルネットワークを使えば良いのです。事前に「画像の偽物らしさを出力するニューラルネットワーク」を作っておきます。これは識別器と呼ぶことにしましょう。また、これに倣って今後生成モデルのことを生成器と呼ぶことにしましょう。識別器を生成器の学習時、具体的には生成器が生成した画像の偽物らしさを求める時に使用します。こうすれば、偽物らしさを生成器のパラメータで微分することが出来るので、パラメータの勾配が求まりそうですね。

またここで、もう一つ工夫を加えます。実は事前に強い識別器を作ってしまうと上手く学習が進みません。生成器は識別器を騙そうとする訳ですが、識別器が賢すぎるとどうすれば騙せるのかが分からないといった感じです。そこで、生成器の学習と並行して識別器を学習させます。生成器の成長に合わせて識別器を強くしていく感じです。こうすることで学習が上手くいくようになります。生成器・識別器が徐々に成長し、最終的に生成器は高度な画像が生成できるようになるのです。これが敵対的学習であり、この生成器と識別器の二つのニューラルネットワークを用いた構造を敵対的生成ネットワーク（GAN） といいます。

実装

理論の説明が終わったので、実装していきましょう。今回は、乱数からMNISTの手書き数字の画像を生成するモデルを作ります。
言語はPython、フレームワークはPyTorchを用います。

import torch
from torch import nn, optim
from torch.utils.data import DataLoader
import torchvision
from torchvision.datasets import MNIST
from torchvision import transforms
from IPython.display import display

batch_size = 64 # バッチサイズ
nz = 100 # 潜在変数の次元数
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

潜在変数とは生成器に入力する乱数のことですね。ノイズとも呼ばれます。今回はその次元数を100としたので、100個の乱数からなるベクトルを生成器に与えることになります。

MNIST

手書き数字のデータセットです。こんな画像。

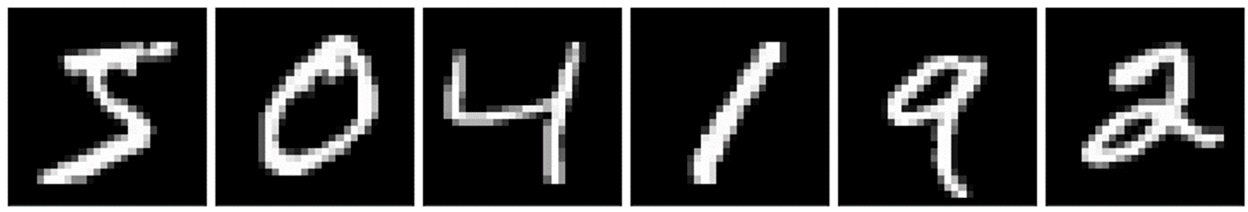
これが、生成したい画像の目標となるデータになります。先ほど「正解はいらない」と述べましたが、それはあくまで入力と一対一に対応する正解がいらないだけで、生成したいデータのお手本のようなものは必要になります。識別器を学習させるためですね。以後このお手本のデータを「本物」と呼ぶことにしましょう。

dataset = MNIST(
    root="data",
    train=True,
    download=True,
    transform=transforms.ToTensor()
)

dataloader = DataLoader(
    dataset,
    batch_size=batch_size,
    shuffle=True,
    drop_last=True # バッチサイズがずれると面倒くさいので最後は切り捨て
)

sample_x, _ = next(iter(dataloader))
w, h = sample_x.shape[2:] # (28, 28)
image_size = w * h        # 784

データセットをバッチサイズで割り切れなかった場合は最後に余りが生じるのですが、PyTorchでのGANの実装の場合それがあると面倒くさいので、drop_last=Trueとして除外しています。

識別器

画像を入力すると、それが偽物である確率を出力します。全結合層とReLUで簡単なものを実装します。

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Flatten(), # 1x28x28 -> 784
            nn.Linear(image_size, 512),
            nn.ReLU(),
            nn.Linear(512, 128),
            nn.ReLU()
            nn.Linear(128, 1),
            nn.Sigmoid(), # 確率なので0~1に
        )

    def forward(self, x):
        y = self.net(x)
        return y

画像はもともと縦×横の2次元のデータになっているため、nn.Flatten()で一列に並べます。そして最後にシグモイド関数をかけて0~1の確率にします。

生成器

ノイズから画像を生成します。これは全結合層とReLUとバッチ正規化層で構成します。バッチ正規化がないと上手く画像を生成できないようです。

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            self._linear(nz, 128),
            self._linear(128, 256),
            self._linear(256, 512),
            nn.Linear(512, image_size),
            nn.Sigmoid() # 濃淡を0~1に
        )

    def _linear(self, input_size, output_size):
        return nn.Sequential(
            nn.Linear(input_size, output_size),
            nn.BatchNorm1d(output_size),
            nn.ReLU()
        )

    def forward(self, x):
        y = self.net(x)
        y = y.view(-1, 1, w, h) # 784 -> 1x28x28
        return y

全結合 → バッチ正規化 → ReLUの流れを_linear()関数にまとめました。またこちらでも最後にシグモイド関数をかけて出力値を0~1にしています。これは各画素の濃淡を表しています。そしてそれを縦×横の二次元のデータに直して出力します。

学習

二つのニューラルネットワークを学習させる部分です。敵対的学習ですね。
識別器の学習 → 生成器の学習 を繰り返します。

識別器の学習

生成器が生成した偽物を入力したときは1、本物を入力したときは0が出力されるように学習します。偽物・本物の二値分類タスクという感じです。損失関数には交差エントロピーを使います。

real_labels = torch.zeros(batch_size, 1).to(device) # 本物のラベル
fake_labels = torch.ones(batch_size, 1).to(device) # 偽物のラベル
criterion = nn.BCELoss() # バイナリ交差エントロピー

識別器の学習部分はこんな感じです

z = make_noise(batch_size) # ノイズを生成
fake = netG(z) # 偽物を生成
pred_fake = netD(fake) # 偽物を判定
pred_real = netD(x) # 本物を判定
loss_fake = criterion(pred_fake, fake_labels) # 偽物の判定に対する誤差
loss_real = criterion(pred_real, real_labels) # 本物の判定に対する誤差
lossD = loss_fake + loss_real # 二つの誤差の和
lossD.backward() # 逆伝播
optimD.step() # パラメータ更新

あとで定義しますが、各変数の説明は以下になります。

• make_noise(): ノイズを生成する関数
• netG: 生成器
• netD: 識別器
• x: 本物のミニバッチ
• optimD: 識別器の最適化関数

生成器の学習

「識別器に0を出力してもらえるような画像」を生成できるように学習します。optimGは生成器の最適化関数です。

fake = netG(z) # 偽物を生成
pred = netD(fake) # 偽物を判定
lossG = pred.sum() # 和をとる
lossG.backward() # 逆伝播
optimG.step() # パラメータ更新

0にしたい = 小さくしたいと捉えられるので、生成した画像に対する識別器の出力をそのまま誤差として扱って逆伝播を行います。また和ではなく平均をとることも考えられますが、バッチサイズで割る分勾配が小さくなってしまうので、学習率などをいじる必要があるかもしれません。

なお、一般的にはこのような誤差の取り方をせず、識別器と同じように交差エントロピーを使って誤差を求めます。こんな感じですね。

pred = netD(fake)
lossG = criterion(pred, real_labels)

この方が誤差が指数関数的になるので学習が上手く進むのだと思います。また交差エントロピーを使う場合は0, 1の値はどちらでもよくなりますが、本物を1, 偽物を0と本記事とは逆で実装されていることが多い気がします。理由は分かりません。

関数化

ここまでを関数にまとめてみましょう。

# ノイズを生成する関数
def make_noise(batch_size):
    return torch.randn(batch_size, nz, device=device)

# 画像を描画する関数
def write(netG, n_rows=1, n_cols=8, size=64):
    z = make_noise(n_rows*n_cols)
    images = netG(z)
    images = transforms.Resize(size)(images)
    img = torchvision.utils.make_grid(images, n_cols)
    img = transforms.functional.to_pil_image(img)
    display(img)

real_labels = torch.zeros(batch_size, 1).to(device) # 本物のラベル
fake_labels = torch.ones(batch_size, 1).to(device) # 偽物のラベル
criterion = nn.BCELoss() # バイナリ交差エントロピー

# 学習を行う関数
def train(netD, netG, optimD, optimG, n_epochs, write_interval=1):
    # 学習モード
    netD.train()
    netG.train()

    for epoch in range(1, n_epochs+1):
        for x, _ in dataloader:
            x = x.to(device)

            # 勾配をリセット
            optimD.zero_grad()
            optimG.zero_grad()

            # 識別器の学習
            z = make_noise(batch_size) # ノイズを生成
            fake = netG(z) # 偽物を生成
            pred_fake = netD(fake) # 偽物を判定
            pred_real = netD(x) # 本物を判定
            loss_fake = criterion(pred_fake, fake_labels) # 偽物の判定に対する誤差
            loss_real = criterion(pred_real, real_labels) # 本物の判定に対する誤差
            lossD = loss_fake + loss_real # 二つの誤差の和
            lossD.backward() # 逆伝播
            optimD.step() # パラメータ更新

            # 生成器の学習
            fake = netG(z) # 偽物を生成
            pred = netD(fake) # 偽物を判定
            lossG = pred.sum() # 和をとる
            lossG.backward() # 逆伝播
            optimG.step() # パラメータ更新

        print(f'{epoch:>3}epoch | lossD: {lossD:.4f}, lossG: {lossG:.4f}')
        if epoch % write_interval == 0:
            write(netG) # 生成器で画像を生成し描画する

これで必要な関数が揃いました。

学習

では実際に学習させてみましょう。

netD = Discriminator().to(device)
netG = Generator().to(device)
optimD = optim.Adam(netD.parameters(), lr=0.0002)
optimG = optim.Adam(netG.parameters(), lr=0.0002)
n_epochs = 5

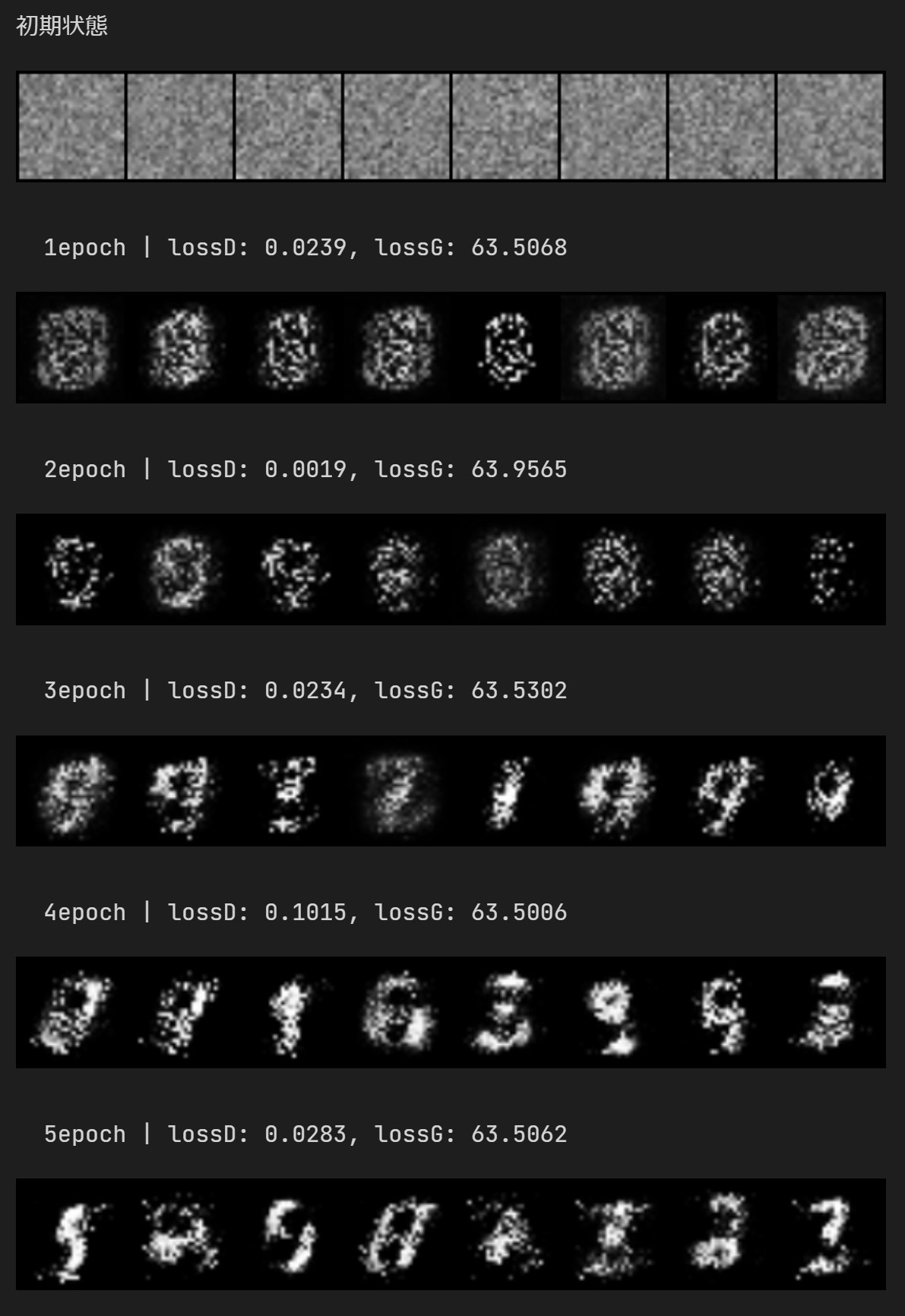
print('初期状態')
write(netG)
train(netD, netG, optimD, optimG, n_epochs)

これを実行するとこうなります。

初期状態は完全ランダムとみて良いですね。そこから学習が進むにつれて徐々に変化していき、5epochの時点でちょっとそれっぽくなってきましたね。

ではもう20epochぐらい回してみましょう。

train(netD, netG, optimD, optimG, 20)

経過はこうなりました。

だんだんと画像に近づいていますね。最終的に出来上がったモデルでもう少し画像を生成してみましょう。

ちょっと線が汚いですが、まあ十分ではないでしょうか。

おわり

おわりです。上記のプログラムはこちらのノートブックにまとめました。気になる人は見てみてください。

追記：
CGANについても書いてみました。
CGAN（条件付きGAN）のシンプルな理解と実装 - Qiita