この記事は私のブログからの転載です。Qiitaに投稿した方が多くの人に届くだろうと思い、こちらにも投稿することにしました。あと宣伝。
記法などの関係でいくらかの内容を省いています。もしよろしければ元記事の方もご覧ください。元記事: Lasso回帰の理論と実装
線形回帰と正則化
Lasso回帰を学ぶ前に軽く予習をしよう。
線形回帰では入力$\boldsymbol x\in\mathbb R^m$と重みパラメータ$\boldsymbol w\in\mathbb R^m$の内積をとることでターゲット$y$を予測する。
\begin{align}
\hat y = \boldsymbol x^\top\boldsymbol w
\end{align}
入力とそれに対応するターゲットが$n$組得られたとする。これらを
- $X\in\mathbb R^{n\times m}$
- $\boldsymbol y\in\mathbb R^n$
と表しておく。
最小二乗法による最適化では、予測値と正解の二乗和誤差が最小になるようなパラメータ$\boldsymbol w$を求める。これは目的関数を微分して$=0$とおくことで解析的に求められる。
\begin{align}
J_\text{LR}(\boldsymbol w) &= \frac{1}{2} \| \boldsymbol y - X\boldsymbol w \|_2^2 \\
\frac{\partial J_\text{LR}}{\partial \boldsymbol w} &= X^\top X\boldsymbol w - X^\top\boldsymbol y \\
\hat{\boldsymbol w} &= (X^\top X)^{-1}X^\top\boldsymbol y
\end{align}
過学習を防ぐため、目的関数に正則化項を足すことがある。パラメータの二乗和で正則化を行う線形回帰はRidge回帰と呼ばれる。二乗和はL2ノルムで表せるのでL2正則化とも呼ばれる。この場合も同様の流れで解析解が得られる。
\begin{align}
J_\text{Rid}(\boldsymbol w) &= \frac{1}{2} \| \boldsymbol y - X\boldsymbol w \|_2^2 + \frac{1}{2}\alpha\|\boldsymbol w\|_2^2 \\
\frac{\partial J_\text{Rid}}{\partial \boldsymbol w} &= X^\top X\boldsymbol w - X^\top\boldsymbol y + \alpha\boldsymbol w \\
\hat{\boldsymbol w} &= (X^\top X + \alpha I)^{-1}X^\top\boldsymbol y
\end{align}
Lasso回帰
Least Absolute Shrinkage and Selection Operator
Lasso回帰では正則化項にパラメータの絶対値の和を用いる。絶対値の和はL1ノルムで表せるのでL1正則化とも呼ばれる。
\begin{align}
J_\text{Las}(\boldsymbol w) = \frac{1}{2} \| \boldsymbol y - &X \boldsymbol w \|_2^2 + \alpha \| \boldsymbol w \|_1 \\
\| \boldsymbol w \|_1 &= \sum_i |w_i|
\end{align}
Lasso回帰はRidge回帰と異なり解析解が得られない。絶対値が含まれているため微分が出来ないためである。本稿ではそんなLasso回帰の最適化について、その理論と実装方法をまとめる。
座標降下法
Coordinate Descent
最適化対象の変数を一つずつ順番に最適化する手法。Lasso回帰の最適化においてもこの手法がよく用いられる。
例えば$\boldsymbol\theta = (\theta_1,\theta_2,\ldots,\theta_m)^\top$の最適化を行うとき、$\boldsymbol\theta$を一度に最適化するのではなく、個別の変数$\theta_i$を$i=1$から$m$まで順に最適化していく。$\theta_i$の最適化はそれ以外の変数$\theta_j,(j\neq i)$を固定して行う。これを収束するまで繰り返す。
勾配降下法同様、目的関数が凸関数でないと局所解に陥る可能性がある。一方で勾配降下法とは異なり、目的関数が微分可能でなくとも適用できるという汎用性がある。微分は出来ないが、ある一つの変数に着目した場合の最適解は求められる、といった少し特殊なケースで活躍する。
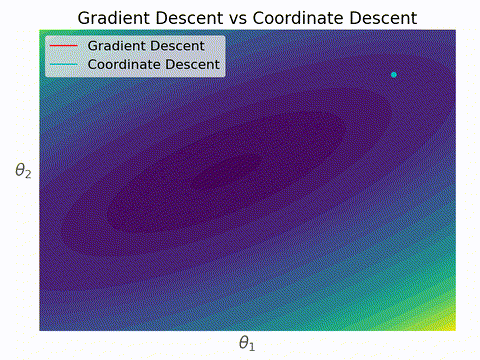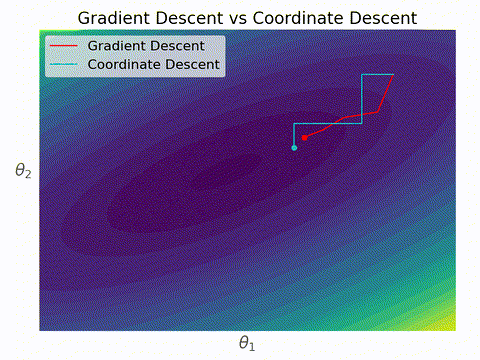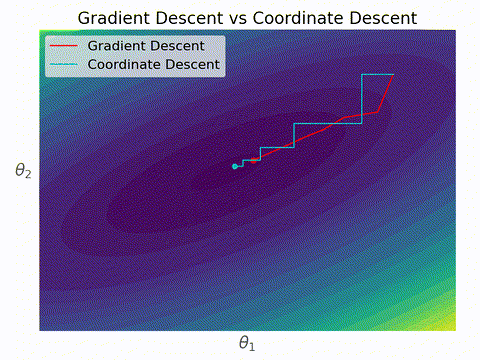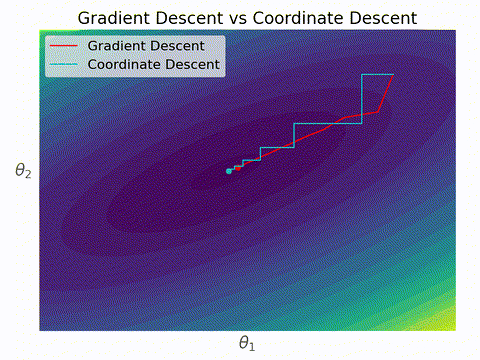
勾配降下法と座標降下法の違いはこんなイメージ。座標降下法では各ステップにおいて一つの変数しか更新されないため、いずれかの軸に対して並行に移動する。
劣微分
Subgradient
微分の定義を少し拡張したようなもの。微分の一般化とも見られる。関数$f(x)$の$x=a$における劣微分を次のように定義する。
任意の$x$に対して$f(x)\geq f(a)+c(x-a)$を満たすような$c$の集合
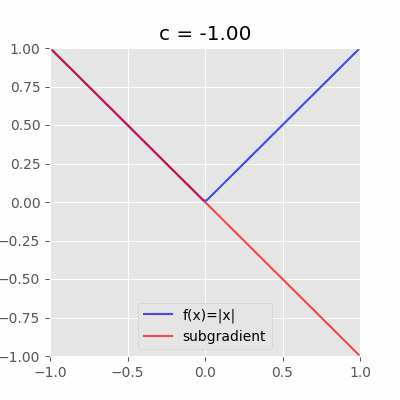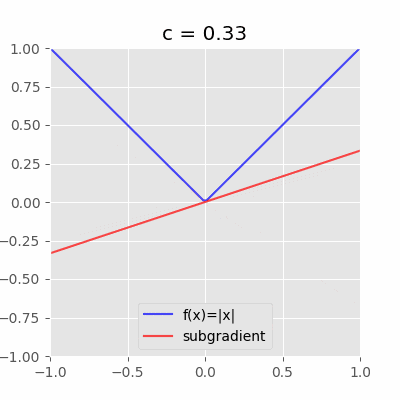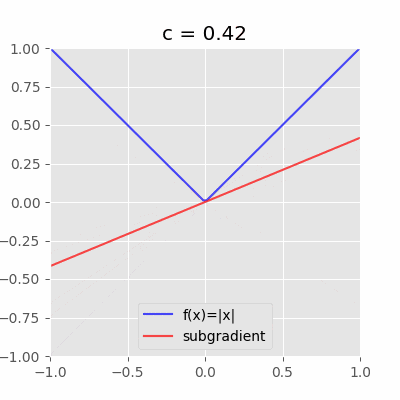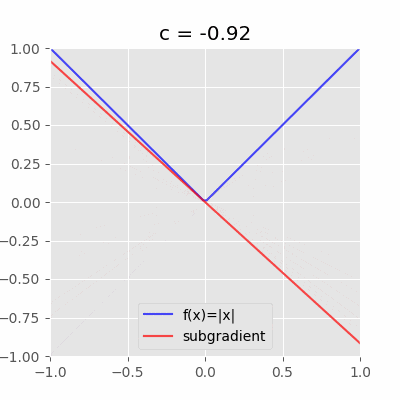
具体的な図を見るとわかりやすい。例えば、$f(x)=|x|$の$x=0$における劣微分は$[-1,1]$である。
「$x=0$を通り且つ$f(x)$を超えない直線(動画の赤い直線)の傾き$c$」が全て$x=0$における劣微分となる。今回の場合は$-1 \leq c \leq 1$の範囲。ちなみに$c$は劣勾配と呼ぶ。
以上を踏まえると、$f(x)=|x|$の微分を以下に定義できる。
\begin{align}
f'(x) = \begin{cases}
-1 & (x<0) \\
[-1,1] & (x=0) \\
1 & (x>0) \\
\end{cases}
\end{align}
こうすることで、絶対値を含む関数での微分が考えられるようになる。
絶対値を含む関数の最適化
劣微分を使って、絶対値を含む下に凸な関数を最適化(最小化)する。
通常の下に凸な二次関数は、微分をして0になる点が最小値となる。しかし、絶対値を含む関数は素直に微分ができないので、劣微分を用いる。劣微分に0が含まれる点を求めることで最適解が得られる。例えば$f(x)=|x|$の場合、$x=0$のときに$0\in f'(x)=[-1,1]$になるので$x=0$が最適解となる。
もう少し複雑な関数も考えてみよう。
\begin{align}
f(x) = ax^2 + b&x + c + d|x| \\
a, d &> 0
\end{align}
二次関数に絶対値を足した。これは下に凸の関数である。この関数を最小化する$x$を求めよう。劣微分に0が含まれる点を求める。
まず微分する。
\begin{align}
f'(x) = 2ax + b + d(|x|)'
\end{align}
ここで、
\begin{align}
(|x|)' = \begin{cases}
-1 & (x<0) \\
[-1,1] & (x=0) \\
1 & (x>0) \\
\end{cases}
\end{align}
より、
\begin{align}
f'(x) = \begin{cases}
2ax + b - d & (x<0) \\
[2ax + b - d, 2ax + b + d] & (x=0) \\
2ax + b + d & (x>0) \\
\end{cases}
\end{align}
あとはこれが0になる(0を含む)$x$を求める。
まず$x<0$の範囲を考える。$f'(x)=0$を解く。
\begin{align}
f'(x) &= 0 \\
2ax + b - d &= 0 \\
x &= -\frac{b-d}{2a}
\end{align}
そしてこの$x$が$<0$となるのは$b>d$の時なので、$b>d$の時、$x=-(b-d)/2a$が$f(x)$の最適解となる。
同じように$x>0$の範囲を考える。
\begin{align}
f'(x) &= 0 \\
2ax + b + d &= 0 \\
x &= -\frac{b+d}{2a}
\end{align}
そしてこの$x$が$>0$となるのは$b<-d$の時なので、$b<-d$の時、$x=-(b+d)/2a$が$f(x)$の最適解となる。
最後に、どちらにも当てはまらない時、つまり$-d\leq b\leq d$の時を考えるが、$x<0$でも$x>0$でもないことが確定しているので、$x=0$が$f(x)$の最適解となる。
まとめるとこうなる。
\begin{align}
\text{argmin}_x \, f(x) = \begin{cases}
-\frac{b+d}{2a} & (b<-d) \\
0 & (-d\leq b\leq d) \\
-\frac{b-d}{2a} & (b>d) \\
\end{cases}
\end{align}
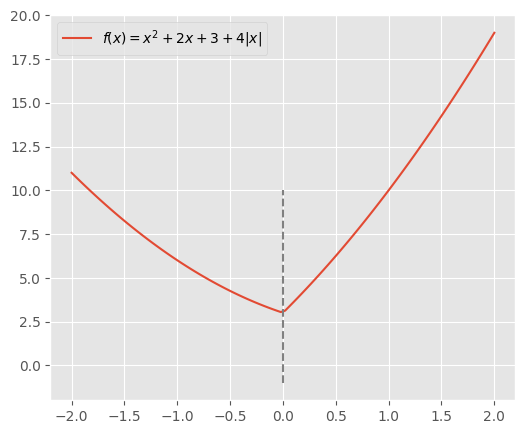
例を見てみよう。$a, b, c, d = 1, 2, 3, 4$とすると、$-d\leq b\leq d$になるので$x=0$が最適解となる。
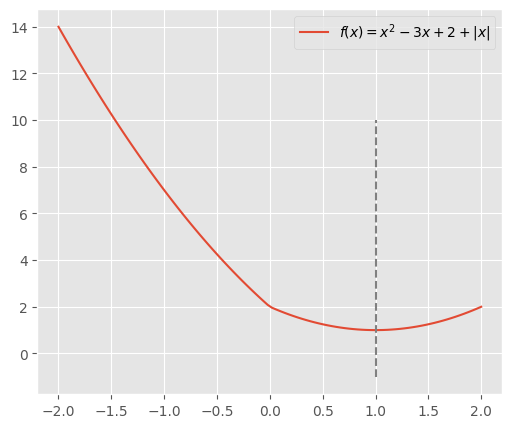
また$a, b, c, d = 1, -3, 2, 1$とすると、$b<-d$になるので
\begin{align}
x = -\frac{b+d}{2a}=-\frac{-3+1}{2\cdot1} = 1
\end{align}
が最適解となる。
ソフト閾値関数
Soft-Thresholding Function
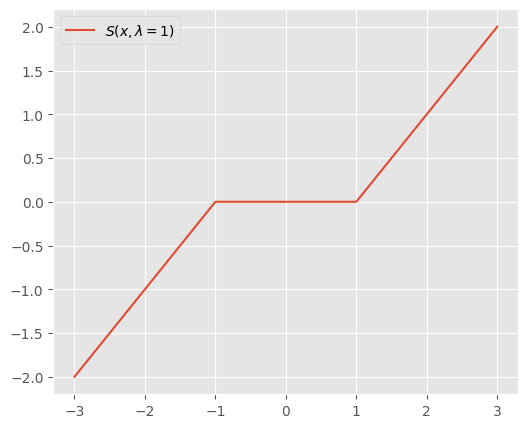
以下の関数をソフト閾値関数や軟閾値作用素と呼ぶ。
\begin{align}
S(x, \lambda)
&= \text{sign}(x) \max(|x|-\lambda, 0) \\
&= \begin{cases}
x+\lambda & (x<-\lambda) \\
0 & (-\lambda\leq x\leq \lambda) \\
x-\lambda & (x>\lambda) \\
\end{cases} \\
\lambda &\geq 0
\end{align}
Pythonで書くとこう。
def soft_thresholding(x, threshold):
return np.sign(x) * np.maximum(np.abs(x) - threshold, 0)
$\lambda=1$とすると、こんなグラフ。
$\lambda$を大きくすると0になる範囲が広がる。
この関数を用いると、先の解を以下のように表せる。
\begin{align}
\text{argmin}_x \, f(x)
&= \begin{cases}
-\frac{b+d}{2a} & (b<-d) \\
0 & (-d\leq b\leq d) \\
-\frac{b-d}{2a} & (b>d) \\
\end{cases} \\
&= S\left(-\frac{b}{2a}, \frac{d}{2a}\right)
\end{align}
Lasso回帰の最適化
ではいよいよLasso回帰の最適化を行おう。目的関数は以下とする。
\begin{align}
J_\text{Las}(\boldsymbol w) = \frac{1}{2N}\| \boldsymbol y - X \boldsymbol w \|_2^2 + \alpha \| \boldsymbol w \|_1
\end{align}
scikit-learnに倣い、一項目をデータ数$N$で割った。どうせ$\alpha$で比重を調整できるので定数を掛けても問題ない。$N$で割っておくと$\alpha$に関する議論で$N$をあまり意識しなくてよくなる(データ数に応じて$\alpha$を調整する必要がなくなる)。
座標降下法を用いて最適化を行う。ある一つのパラメータ$w_i$に着目し、それ以外のパラメータ$w_j,(i\neq j)$を固定した状態で$w_i$を最小化する。
目的関数を$w_i$について整理しよう。
\begin{align}
J_\text{Las}(w_i)
&= \frac{1}{2N} \| \boldsymbol y - X \boldsymbol w \|_2^2 + \alpha \| \boldsymbol w \|_1 \\
&= \frac{1}{2N} \sum_{n=1}^N \left( y^{(n)} - \boldsymbol w^\top\boldsymbol x^{(n)} \right)^2 + \alpha \| \boldsymbol w \|_1 \\
&= \frac{1}{2N} \sum_{n=1}^N \left( y^{(n)} - \boldsymbol w_{\backslash i}^\top\boldsymbol x_{\backslash i}^{(n)} - w_ix_i^{(n)} \right)^2 + \alpha(\| \boldsymbol w_{\backslash i} \|_1 + |w_i|) \\
\end{align}
$\boldsymbol x_{\backslash i}$は$\boldsymbol x$の$i$番目の要素$x_i$以外を並べたベクトル。今後のために$i$とそれ以外で分けた。
ここで以下を定義する。
\begin{align}
r_{\backslash i}^{(n)} &= y^{(n)} - \boldsymbol w_{\backslash i}^\top\boldsymbol x_{\backslash i}^{(n)} \\
\boldsymbol r_{\backslash i} &= (r_{\backslash i}^{(1)}, r_{\backslash i}^{(2)}, \cdots, r_{\backslash i}^{(N)})^\top \in \mathbb R^N \\
\boldsymbol x_i &= (x_i^{(1)}, x_i^{(2)}, \cdots, x_i^{(N)})^\top \in \mathbb R^N
\end{align}
$r_{\backslash i}^{(n)}$は$\boldsymbol x^{(n)}$の$i$番目の特徴量$x_i^{(n)}$を考慮せずに予測した値の誤差。$\boldsymbol r_{\backslash i}$はそれらを並べたベクトル。$\boldsymbol x_i$は$i$番目の特徴量を並べたベクトル。これで変形を進める。
\begin{align}
&= \frac{1}{2N} \sum_{n=1}^N \left( r_{\backslash i}^{(n)} - w_ix_i^{(n)} \right)^2 + \alpha(\| \boldsymbol w_{\backslash i} \|_1 + |w_i|) \\
&= \frac{1}{2N}\sum_{n=1}^N \left( (r_{\backslash i}^{(n)})^2 - 2r_{\backslash i}^{(n)}w_ix_i^{(n)} + (w_ix_i^{(n)})^2 \right) + \alpha(\| \boldsymbol w_{\backslash i} \|_1 + |w_i|) \\
&= \frac{1}{2N}\sum_{n=1}^N \left( -2r_{\backslash i}^{(n)}w_ix_i^{(n)} + (w_ix_i^{(n)})^2 \right) + \alpha |w_i| + \text{const} \\
\end{align}
$w_i$に関係のない項を定数として$\text{const}$にまとめた。さらに変形を進めて
\begin{align}
&= \frac{1}{2N} \left( -2w_i \sum_{n=1}^N r_{\backslash i}^{(n)}x_i^{(n)} + w_i^2 \sum_{n=1}^N (x_i^{(n)})^2 \right) + \alpha |w_i| + \text{const} \\
&= \frac{1}{2N} \left( -2w_i\boldsymbol r_{\backslash i}^\top\boldsymbol x_i + w_i^2\|\boldsymbol x_i\|_2^2 \right) + \alpha |w_i| + \text{const} \\
&= -\frac{1}{N}w_i\boldsymbol r_{\backslash i}^\top\boldsymbol x_i + \frac{1}{2N}w_i^2\|\boldsymbol x_i\|_2^2 + \alpha |w_i| + \text{const} \\
\end{align}
$w_i^2$について整理すると
\begin{align}
J_\text{Las}(w_i) = \frac{1}{2N} \| \boldsymbol x_i \|_2^2w_i^2 - \frac{1}{N}\boldsymbol r_{\backslash i}^\top\boldsymbol x_iw_i + \text{const} + \alpha|w_i|
\end{align}
前章で解いた$f(x)=ax^2+bx+c+d|x|\quad(a, d > 0)$と同じ形になった。この解は$S\left(-\frac{b}{2a}, \frac{d}{2a}\right)$であるため、
\begin{align}
a &= \frac{1}{2N} \| \boldsymbol x_i \|_2^2 \\
b &= -\frac{1}{N}\boldsymbol r_{\backslash i}^\top\boldsymbol x_i \\
d &= \alpha \\
\end{align}
を代入すると
\begin{align}
\text{argmin}_{ \,w_i} J_\text{Las}(w_i) = S \left( \frac{\boldsymbol r_{\backslash i}^\top\boldsymbol x_i}{\|\boldsymbol x_i\|_2^2}, \frac{N\alpha}{\|\boldsymbol x_i\|_2^2} \right)
\end{align}
が得られる。これが各ステップにおける$w_i$の更新先となる。
また、バイアス項に対応するパラメータは正則化をしないので、解が変わる。$w_0$をバイアスとし、正則化項を無視すると、
\begin{align}
J_\text{Las}(w_0) = \frac{1}{2N} \|\boldsymbol x_0 \|_2^2w_0^2 - \frac{1}{N}\boldsymbol r_{\backslash 0}^\top\boldsymbol x_0w_0 + \text{const}
\end{align}
となるので、これを微分し、
\begin{align}
\frac{\partial J_\text{Las}}{\partial w_0} = \frac{1}{N}\|\boldsymbol x_0\|_2^2w_0 - \frac{1}{N}\boldsymbol r_{\backslash 0}^\top\boldsymbol x_0
\end{align}
$=0$とおいて$w_0$について解く。
\begin{align}
w_0 = \frac{\boldsymbol r_{\backslash 0}^\top\boldsymbol x_0}{\|\boldsymbol x_0\|_2^2}
\end{align}
$w_0$をバイアスとする場合、$\boldsymbol x_0=(1, 1, \cdots, 1)^\top\in\mathbb R^N$となるので、
\begin{align}
w_0
&= \frac{\sum_{n=1}^Nr_{\backslash 0}^{(n)}}{N} \\
&= \bar{r_{\backslash 0}} \\
\end{align}
となる。バイアス項を無視した予測値と正解の差の平均だね。
以上で全てのパラメータの更新先が得られた。最後にLasso回帰の最適化手順をまとめる。
- $\boldsymbol w$を初期化
- $w_0$を最適化: $w_0 \leftarrow \bar{r_{\backslash 0}}$
- $w_1, w_2, \cdots, w_m$を最適化: $w_i \leftarrow S \left( \frac{\boldsymbol r_{\backslash i}^\top\boldsymbol x_i}{|\boldsymbol x_i|_2^2}, \frac{N\alpha}{|\boldsymbol x_i|_2^2} \right)$
- 収束するまで2, 3を繰り返す
Python実装
実装してみよう。
import numpy as np
class Lasso:
def __init__(self, alpha: float = 1., max_iter: int = 1000):
self.alpha = alpha
self.max_iter = max_iter # 繰り返しの上限
self.weights = None
@staticmethod
def soft_thresholding(x, threshold):
return np.sign(x) * np.maximum(np.abs(x) - threshold, 0)
def fit(self, X, y):
X = np.insert(X, 0, 1, axis=1)
n_samples, n_features = X.shape
self.weights = np.zeros(n_features) # パラメータの初期化
for _ in range(self.max_iter): # 上限まで繰り返し
# w0の更新
self.weights[0] = np.mean(y - X[:, 1:] @ self.weights[1:])
# w1, w2, ..., wmの更新
for i in range(1, n_features):
r_i = y - np.delete(X, i, 1) @ np.delete(self.weights, i)
x_i = X[:, i]
norm = np.linalg.norm(x_i) ** 2
self.weights[i] = self.soft_thresholding(
r_i @ x_i / norm, n_samples * self.alpha / norm
)
def predict(self, X):
X = np.insert(X, 0, 1, axis=1)
return X @ self.weights
収束するまでと書いたが、コードをシンプルにするため、繰り返しの上限max_iterを導入し、上限に達したら終了するようにした。
適当なデータで学習させてみる。
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True)
model = Lasso(alpha=1.)
model.fit(X, y)
print("\n".join(model.weights.astype(str).tolist()))
152.133484162896
0.0
-0.0
367.70162582143126
6.30970264417499
0.0
0.0
-0.0
0.0
307.60214746219583
0.0
sklearnとも一致する。
from sklearn.linear_model import Lasso as LassoSklearn
model = LassoSklearn(alpha=1., tol=0., max_iter=1000)
model.fit(X, y)
weights = np.append([model.intercept_], model.coef_)
print("\n".join(weights.astype(str).tolist()))
152.133484162896
0.0
-0.0
367.70162582143115
6.309702644174996
0.0
0.0
-0.0
0.0
307.6021474621959
0.0
微小な誤差が生じているが、細かい実装方法が違うだけかな。
Lasso回帰の性質
最適化から離れた、ちょっとしたLasso回帰の小話
スパース推定
前章で得られた解を見てみると、多くの要素が0になっていることが分かる。このような多くの要素が0であるベクトルはスパースなベクトルや疎ベクトルと呼ばれる。反対に多くの要素が0でないベクトルは密ベクトルと呼ばれる。
こういったスパースな解を得ることはスパース推定やスパースモデリングと呼ばれる。スパース推定によって多くのデータの中から重要なデータのみを取り出すことができる。Lasso回帰では、複数の特徴量の中から目的変数の予測に寄与するものだけを取り出すことができる。Lasso回帰は特徴量選択という面で非常に解釈性の高いモデルと言える。
なぜLasso回帰によってスパースな解が得られるかはパラメータの更新式を見ると分かりやすい。
\begin{align}
w_i \leftarrow S \left( \frac{\boldsymbol r_{\backslash i}^\top\boldsymbol x_i}{\|\boldsymbol x_i\|_2^2}, \frac{N\alpha}{\|\boldsymbol x_i\|_2^2} \right)
\end{align}
ソフト閾値関数$S(x, \lambda)$は$x$の絶対値が閾値$\lambda$を超えない場合に0となる関数である。$\alpha$を大きくすると閾値が大きくなり、結果、$w_i$が0になることが多くなる。
ちなみに、L1ではなくL0ノルムによる正則化を行う手法もある。L0ノルムはベクトルの非ゼロの要素の数を表すため、より厳密なスパース推定が可能になる。ただ計算量的に最適化が困難であるため、多くの場合はL1ノルムによる正則化が用いられる。
ベイズ的解釈
線形回帰の最小二乗法は誤差に正規分布を仮定した最尤推定と解釈できる。実際にその仮定で対数尤度の計算を進めると
\begin{align}
p(y|\boldsymbol x; \boldsymbol w) &= \mathcal N(y; \boldsymbol w^\top\boldsymbol x,1) \\
\ln p(\boldsymbol y| X; \boldsymbol w)
&= \sum_n \ln p(y^{(n)}| \boldsymbol x^{(n)}; \boldsymbol w) \\
&= \sum_n \ln \left( \frac{1}{\sqrt{2\pi}} \exp \left( -\frac{(y^{(n)} - \boldsymbol w^\top \boldsymbol x^{(n)})^2}{2} \right) \right) \\
&= -\frac{1}{2} \sum_n (y^{(n)} - \boldsymbol w^\top \boldsymbol x^{(n)})^2 + \text{const} \\
&= -\frac{1}{2} \| \boldsymbol y - X\boldsymbol w \|_2^2 + \text{const}
\end{align}
負の二乗和誤差が出てくる。この最大化は二乗和誤差の最小化と同じである。ではここに正則化項を足すことは何を意味するか。
ここに正則化項を足すことは、確率モデルに事前分布$p(\boldsymbol w)$を仮定することと同じ意味になる。例えばL2正則化はパラメータの事前分布として平均0の正規分布を仮定することと解釈できる。
\begin{align}
p(\boldsymbol w) &= \mathcal N(\boldsymbol w; \boldsymbol 0, \frac{1}{\lambda} I) \\
\ln p(\boldsymbol w| X, \boldsymbol y)
&= \ln p(\boldsymbol y| X; \boldsymbol w) + \ln p(\boldsymbol w) \\
&= -\frac{1}{2} \| \boldsymbol y - X\boldsymbol w \|_2^2 - \frac{1}{2}\lambda \| \boldsymbol w\|_2^2 + \text{const}
\end{align}
Lasso回帰はL1正則化を行うが、これはパラメータの事前分布としてラプラス分布を仮定していると解釈できる。
\begin{align}
p(\boldsymbol w) &= \text{Lap}(\boldsymbol w; \boldsymbol 0, \lambda) \\
\ln p(\boldsymbol w| X, \boldsymbol y)
&= \ln p(\boldsymbol y| X; \boldsymbol w) + \ln p(\boldsymbol w) \\
&= -\frac{1}{2} \| \boldsymbol y - X\boldsymbol w \|_2^2 - \lambda \| \boldsymbol w\|_1 + \text{const} \\
\end{align}
このあたりの細かい話は別の記事に書いたので、興味があればぜひ: 線形回帰における最尤推定・MAP推定・ベイズ推定
ElasticNet
Ridge回帰とLasso回帰を組み合わせたモデル。L1正則化とL2正則化を両方行う。次の目的関数を最適化する。
\begin{align}
J_\text{EN}(\boldsymbol w) = \frac{1}{2N} \| \boldsymbol y - \boldsymbol X \boldsymbol w \|_2^2 + \alpha \left( \beta \| \boldsymbol w \|_1 + (1-\beta) \frac{1}{2} \| \boldsymbol w \|_2^2 \right)
\end{align}
$\beta$はL1正則化の割合を表すハイパーパラメータ。$\beta=1$とするとLasso回帰、$\beta=0$とするとRidge回帰と一致する。
解き方はLassoと一緒。絶対値が含まれているので解析的には解けない。ここでも座標降下法を使う。Lasso同様、ある一つのパラメータ$w_i$に着目した目的関数$J(w_i)$が必要。上の式を変形していっても良いが、面倒くさいので、Lasso回帰とどこが変わったかを考える。
Lasso回帰の目的関数は以下であった。
\begin{align}
J_\text{Las}(w_i) = \frac{1}{2N} \| \boldsymbol x_i \|_2^2w_i^2 - \frac{1}{N} \boldsymbol r_{\backslash i}^\top\boldsymbol x_iw_i + \text{const} + \alpha|w_i|
\end{align}
各項の係数がどう変化するかを考えよう。L2正則化は各パラメータ$w_i$の二乗を足すので、増えた分を二乗の項の係数に足せば良い。つまりハイパーパラメータと定数を掛けた$\alpha(1-\beta)/2$を足せば良い。またL1ノルムには新たなパラメータ$\beta$が追加で掛けられる。これらをまとめるとこうなる。
\begin{align}
J_\text{EN}(w_i) = \frac{1}{2N}(\|\boldsymbol x_i\|_2^2 + N\alpha(1-\beta))w_i^2 - \frac{1}{N}\boldsymbol r_{\backslash i}^\top\boldsymbol x_iw_i + \text{const} + \alpha\beta|w_i|
\end{align}
ここからの解き方は同じ。
\begin{align}
a &= \frac{1}{2N}\big(\|\boldsymbol x_i\|_2^2 + N\alpha(1-\beta)\big) \\
b &= -\frac{1}{N}\boldsymbol r_{\backslash i}^\top\boldsymbol x_i \\
d &= \alpha\beta
\end{align}
とすると、解は$S\left(-\frac{b}{2a}, \frac{d}{2a}\right)$なので
\begin{align}
\text{argmin}_{ \,w_i} J_\text{EN}(w_i) = S \left( \frac{\boldsymbol r_{\backslash i}^\top\boldsymbol x_i}{\|\boldsymbol x_i\|_2^2 + N\alpha(1-\beta)}, \frac{N\alpha\beta}{\|\boldsymbol x_i\|_2^2 + N\alpha(1-\beta)} \right)
\end{align}
が得られる。
またバイアスについては正則化項を考慮しないため先と同じく
\begin{align}
w_0 = \bar{r_{\backslash 0}}
\end{align}
となる。
実装してみよう。
class ElasticNet:
def __init__(
self,
alpha: float = 1.,
beta: float = 0.5,
max_iter: int = 1000
):
self.alpha = alpha
self.beta = beta
self.max_iter = max_iter
self.weights = None
@staticmethod
def soft_thresholding(x, threshold):
return np.sign(x) * np.maximum(np.abs(x) - threshold, 0)
def fit(self, X, y):
X = np.insert(X, 0, 1, axis=1)
n_samples, n_features = X.shape
self.weights = np.zeros(n_features)
for _ in range(self.max_iter):
self.weights[0] = np.mean(y - X[:, 1:] @ self.weights[1:])
for i in range(1, n_features):
r_i = y - np.delete(X, i, 1) @ np.delete(self.weights, i)
x_i = X[:, i]
norm = np.linalg.norm(x_i) ** 2
norm += n_samples * self.alpha * (1 - self.beta) # 追加
self.weights[i] = self.soft_thresholding(
r_i @ x_i / norm,
n_samples * self.alpha * self.beta / norm # 変更
)
def predict(self, X):
X = np.insert(X, 0, 1, axis=1)
return X @ self.weights
更新式が少しだけ変わった。分母はノルムだけではないからnormという変数名を変えるか迷ったけど、normには規格という意味もあるみたいなのでそのままにした。
model = ElasticNet(alpha=1., beta=0.5)
model.fit(X, y)
print("\n".join(model.weights.astype(str).tolist()))
152.13348416289594
0.3590175634148627
0.0
3.259766998005527
2.2043402383839803
0.5286453997828984
0.2509350904357106
-1.8613631921210814
2.1144540777001035
3.105834685472744
1.7698510183435376
sklearnとも一致する。
from sklearn.linear_model import ElasticNet as ElasticNetSklearn
model = ElasticNetSklearn(alpha=1., l1_ratio=0.5, tol=0., max_iter=1000)
model.fit(X, y)
weights = np.append([model.intercept_], model.coef_)
print("\n".join(weights.astype(str).tolist()))
152.13348416289594
0.3590175634148638
0.0
3.2597669980055266
2.204340238383981
0.5286453997828972
0.2509350904357103
-1.8613631921210825
2.1144540777001053
3.105834685472747
1.7698510183435392
オワリ
おつ。