数値相対論ツールキット Einstein Toolkit を動かしてみた

こんにちは。
数値相対論用ツールキットの中で、最もやさしいと言われる Einstein Toolkit を動かしてみたので、そのレポートをしたいと思います。
なお、今回使用しているのは 2025/5/29 版です。

数値相対論とは

一般相対論における Einstein 方程式を数値的に解く手法を研究する物理学の分野です。

数値相対論の重要性

検出器の出力は大変小さいため、重力波検出器で検出されるパターンを予め計算しておき、予測と実測を比較することで、どのような物理現象が発生したか調べます。

Einstein Toolkit とは

数値計算フレームワーク Cactus 上で動作する数値相対論ツールキットです。
https://einsteintoolkit.org/

Cactus とは

MPI, OpenMP を隠ぺいする数値計算フレームワークです。PC からスーパーコンピュータまで動作し、1台でも動作するのが特徴です。
またデータインタフェースが厳密に決まっており、FORTRAN90, C, C++ で書かれたプログラムを混在させることができます。

Einstein Toolkit を実行するための前提条件

ハードウェア条件

今回は中性子星の定常状態を扱うため、それほどリソースは喰いませんが、連星系の衝突等をシミュレートするには多くのリソースが必要になります。今回利用した H/W は以下となります。

項目	内容
CPU	13世代 Core i7 13700KF (3.4GHz) 10 core 20 threads
RAM	DDR4-2400 128GB

ソフトウェア条件

Windows の WSL2 に Ubuntu 24.04.2 をインストールして実施しました。まず、必要な依存ライブラリをインストールします。

sudo apt-get install build-essential libopenmpi-dev openmpi-bin gfortran git subversion curl gnuplot gnuplot-x11

さらに、

sudo apt-get install pkg-config libfftw3-dev libgsl0-dev libatlas-base-dev libjpeg-dev libssl-dev libhdf5-serial-dev libhwloc-dev

これだけだと udev でエラーが出るため、以下を実行しました。

sudo apt-get install libudev-dev

また、make ではなく、scons を利用するため、これもインストールしておきます。

sudo apt-get install scons

Einstein Toolkit のダウンロードと実行

https://einsteintoolkit.org/download.html
に従ってダウンロードします。最初に curl でダウンローダ GetComponents をダウンロードし、これを使って残りのツールキットをダウンロードします。Cactus は GetComponents を実行する際に、自動的にダウンロードされます。GetComponents はこの他に SimFactry, thornlist もダウンロードします。
ホームページではこのほかのコンポーネントをダウンロードするような記述がありますが、中性子星定常状態の設定ファイルは Cactus ディレクトリの下に揃っていますので、必要ありません。

初期化

Einstein Toolkit を初期化し、マシン情報を生成してファイルに書き込みます。
Cactus ディレクトリに入って操作します。

cd ~/Cactus
./simfactory/bin/sim setup-client

ビルド

Thornlist に従ってビルドします。（とても時間がかかります...。20分くらい)

./simfactory/bin/sim build -j10 --thornlist manifest/einsteintoolkit.th

中性子星の定常状態のシミュレーション

par ディレクトリの下の tov_ET.par ファイルを指定してシミュレーションを実行します。

./simfactory/bin/sim create-run tov_ET \
  --parfile=par/tov_ET.par \
  --procs=1 \
  --num-threads=10 \
  --walltime=0:20:0

成功すると、以下のディレクトリが作成されます。(ホーム直下に作成されることに注意。)

~/simulations/tov_ET/output-0000/tov_ET

Kuibit による可視化

可視化ツールは ParaView や GnuPlot など色々ありますが、ここでは python の可視化ツール Kuibit を使ってみます。python3.7 が必要ですが、Ubuntu 24.04.2 は標準で 3.12.3 が入っていますので、問題ありません。依存ライブラリ（NumPy, SciPy, h5py など）も自動でインストールされます。Tk を使って可視化するため、python3-tk もインストールしておきます。

pip3 install kuibit
sudo apt install python3-tk

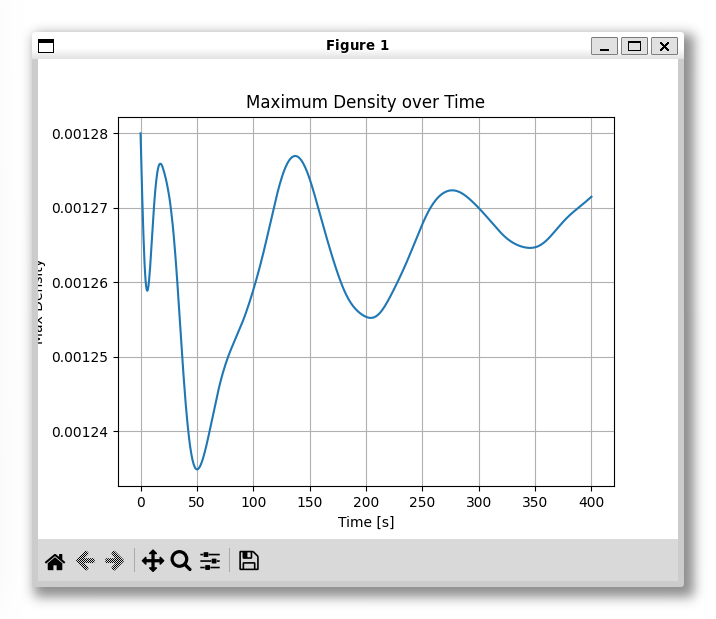
手始めに最大密度の時間変化をプロットしてみます。

from kuibit.simdir import SimDir
import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as plt

sim = SimDir("/home/minosys/simulations/tov_ET/output-0000/tov_ET")
rho_max = sim.timeseries["maximum"]["rho"]

plt.plot(rho_max.t, rho_max.y)
plt.xlabel("Time [s]")
plt.ylabel("Max Density")
plt.title("Maximum Density over Time")
plt.grid()
plt.show()

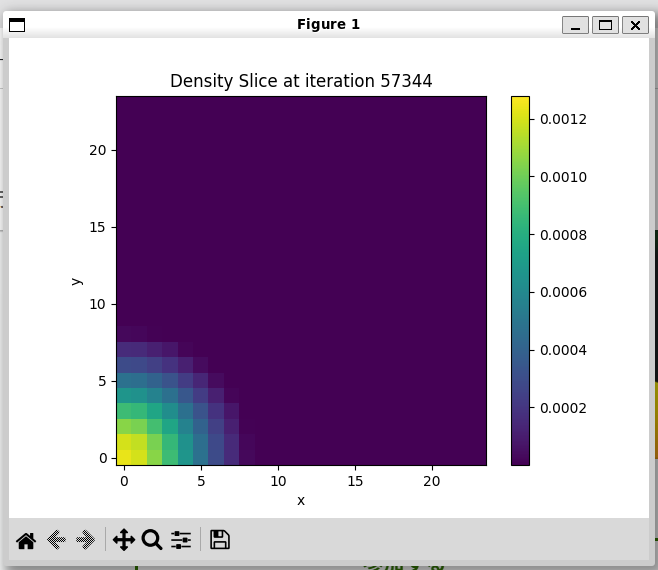
次に、密度の時間変化をアニメーション化します。ただし、定常状態なので、何も変わりません。😜

from kuibit.simdir import SimDir
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np

# シミュレーションディレクトリを指定
sim = SimDir("/home/minosys/simulations/tov_ET/output-0000/tov_ET")

# 変数と平面を指定（例：rho の xy スライス）
grid_xy = sim.gridfunctions["xy"]["rho"]

# 時間ステップを取得
iterations = sorted(grid_xy.iterations)

# 描画の初期設定
fig, ax = plt.subplots()
grid0 = grid_xy[iterations[0]][1]
combined = np.squeeze(np.vstack([d.data_xyz for d in grid0]))
im = ax.imshow(combined,
               origin="lower",
               cmap="viridis")
ax.set_title("Density Slice (xy plane)")
ax.set_xlabel("x")
ax.set_ylabel("y")
plt.colorbar(im, ax=ax)

# アニメーション更新関数
def update(i):
    data = grid_xy[iterations[i]][1]
    combined = np.squeeze(np.vstack([d.data_xyz for d in data]))
    im.set_array(combined)
    ax.set_title(f"Density Slice at iteration {iterations[i]}")
    return [im]

# アニメーション作成
ani = animation.FuncAnimation(fig, update, frames=len(iterations), interval=200)

plt.show()

おわりに

本稿では、数値相対論のシミュレーションを行うツールキットである、Einstein Toolkit について説明しました。
私が学生だった頃(PC-9801 の時代です)は、PC でこのようなシミュレーションができるようになるとは夢にも思いませんでした。
定常状態の中性子星のシミュレーションは動かないので、あまり面白いアニメーションにはなりませんでしたが、そのうち中性子星の衝突やブラックホールの衝突のシミュレーションを実行してみたいと思います。(それには、現在の PC ではリソースが不足していますが。)
現在、このツールは CUDA 等の GPU アクセラレーションには対応していないので、コア数の多い CPU で実行する方が有利ですが、他のフレームワークでは対応しているものがあるようです。

参考文献

他にもありますが、とりあえず読んだものだけ列挙します。
[1] 柴田 大, 「一般相対論の世界を探る」2007, 東京大学出版会
[2] T.W. Baumgarte, S.L.Shapiro, "Numerical Relativity Starting from Scratch", 2021, Cambridge University Press
[3] 重力波検出器

おまけ: grid_xy[z] の構成

grid_xy[z] はリファインメントレベルリストから構成されます。リファインメントレベルとは、メッシュの粗さを表します。例えば、レベル0は空間分解能が2.0, 2.0、レベル1は空間分解能が1.0, 1.0となります。この例では、レベルが上がるにつれ、分解能が上がります。リファインメントレベルリストの要素を kuibit では component と呼びます。
Component は複数のデータチャンク(patch)を持ち、patch のリストとして表現されます。１つの patch は場の部分集合に相当します。