最初に断って起きますが、間違いあったらすみません><
とりあえず有名な活性化関数の良い所と悪い所を見て行きたい!
活性化関数に求められること
-
非線形である事=>非線形を表現する為に活性化関数を使うのに線形だったら意味がない!
-
負の入力に対して出力の値がほぼ0であること=>データには無視したい情報(ノイズ)があり、それを無視する為負の値の入力に対して出力は0を出力すると良い?(ちょっと定かではない)
-
微分の最大値が1であること=>勾配を計算していくのに活性化関数の微分を何層も掛けていく時、1以下の値を掛けると0に近づいていく。
-
活性化関数滑らかであること=>連続的な関数の方が精度が良くなる
sigmoid
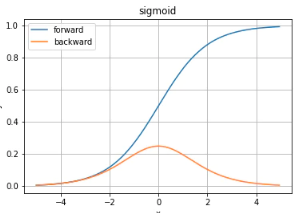sigmoidの微分の最大値は0.25となっているため、sigmoid関数をかけ合わせていくと値がどんどん小さくなり、勾配消失問題を起こす。
tanh
最大値が1となりsigmoidであった勾配消失問題が起こりにくくなった。
入力が極端に大きい所と小さい所では微分が0になる問題がある。学習が進まないよ〜
ReLU
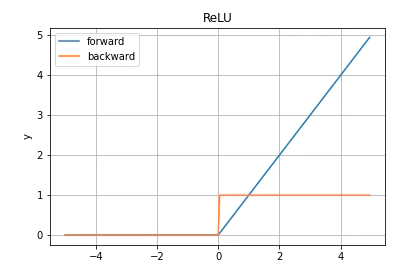利点は正の入力の時傾きが1になり勾配消失が起きないこと。欠点は負の入力の時傾きが0になり学習が進まないこと。
leaky-ReLU
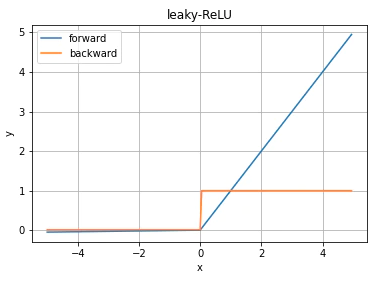ReLUの入力が負の時に学習が進まない問題に対して負の入力が来た時に小さな傾きをつける。
でもあんまり効果がなかったっていう人がいた。
Swish
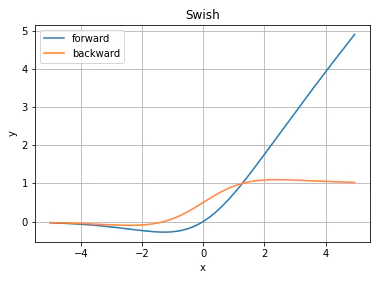ReLUに近いが滑らかな点が精度を上げてれる。ただ計算コストがちょいと上がる。
Mish
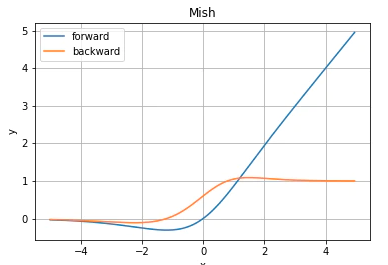Swishの進化系?1次微分の傾きがより急なので、収束が早い。
tanhExp
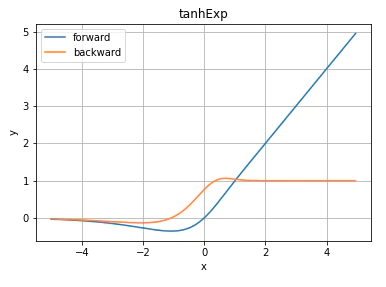Swishの進化系?Mishより1次微分の傾きがより急なので、収束が早くなる所が良い所?!(後日論文確認します)
勾配が1を超えている範囲が小さくなっているのも高評価!
結論
絶対じゃないけどこの4つが活性化関数では重要そう 1. 非線形である事 2. 負の入力に対して出力の値がほぼ0であること 3. 微分の最大値が1であること 4. 活性化関数滑らかであること<参考文献>
Swish
https://arxiv.org/pdf/1710.05941.pdf
Mish: A Self Regularized Non-Monotonic
Activation Function
https://arxiv.org/pdf/1908.08681v3.pdf
活性化関数一覧 (2020)
https://qiita.com/kuroitu/items/73cd401afd463a78115a


