非自明な関数の最大値、または最小値を求める手法は Black-Box最適化 と呼ばれます。Black-Box最適化の中でもベイズの枠組みを用いて、関数の最大値、または最小値を求めていく方法を、 ベイズ最適化(Bayesian Optimization) と呼びます。
Black-box関数最適化では解の1回の評価の計算コストが大きいことを前提としていることが特徴です。深層学習などの1回の評価に数時間かかる場合に、探索にかかる評価回数をいかに少なくできるかが重要となります。
ベイズ最適化は、近年の機械学習の流行に伴い、機械学習のハイパーパラメータのチューニングなどでよく用いられるようになってきました。ベイズ最適化は,Grid Search, Random Searchと比較して効率よく優れた解を求められることが報告されています。[Snoek, 2015]
この記事では、ベイズ最適化を実行するプログラムをゼロから実装してみることで、ベイズ最適化のアルゴリズムへの理解を深めることを目的にしています。
以下の記事では、$f(x)$の最大値を求めることを目標にして進めていきます。
理論的な部分に関しては、簡単にまとめますが、この記事では深くは立ち入らないようにします。理論的な理解も深めたい方は、下記の記事などを参照するのが良いかと思われます。
参考文献
[1] Jasper Snoek, Hugo Larochelle, and Ryan P. Adams. Practical Bayesian Optimization of Machine
Learning Algorithms. 2012.
[2] Jasper Snoek, Hugo Larochelle, and Ryan P. Adams. A Tutorial on Bayesian Optimization of
Expensive Cost Functions, with Application to
Active User Modeling and Hierarchical
Reinforcement Learning. 2010.
[3] Bobak Shahriari, Kevin Swersky, Ziyu Wang, Ryan P. Adams and Nando de Freitas. Taking the Human Out of the Loop: A Review of Bayesian Optimization. 2016.
※注意
この記事は筆者が勉強したことをまとめて、理解を深めるために執筆しています。内容に誤り等があった場合は、コメント等でご指摘いただけると幸いです。
イントロダクション
ベイズ最適化は、$f(x)$の具体的な形がわからないが、$f(x)$の最大値を求めたいときに用いられる手法です。一般的には、一回の評価(機械学習的に表現すると一回の学習)に計算コストがかかる関数の最大値を求める場合などに用いられます。
ベイズ最適化では、評価に大きな計算コストのかかる目的関数$f(x)$の代わりに 代理関数(Surrogate function) を用いて、次の探索点を求めます。このとき、次の探索点を決める関数を 獲得関数(Acquisition function) と呼びます。
上図において、青線が目的関数$f(x)$です。緑線は**代理関数(Surrogate function)**で、緑色の領域は全体の95%の信頼区間を表しています。
ベイズ最適化は,以下の操作を繰り返すことで探索を行います。
- 事前に目的関数$f(x)$からいくつかのサンプルをサンプリングしておく
- 保持しているサンプルを用いて代理関数を計算する
- 代理関数の出力を用いて獲得関数を計算し次の探索点を決める
- 目的関数$f(x)$から獲得関数で決めた探索点をサンプリングする
- 新しいサンプルに既存のサンプルを追加する
- 2~5を繰り返す
サンプル数が増えるにつれて、代理関数がうまく目的関数$f(x)$を近似していき、最終的に代理関数を最大にする点が目的関数$f(x)$も最大にする点となるという仕組みです。
目的関数
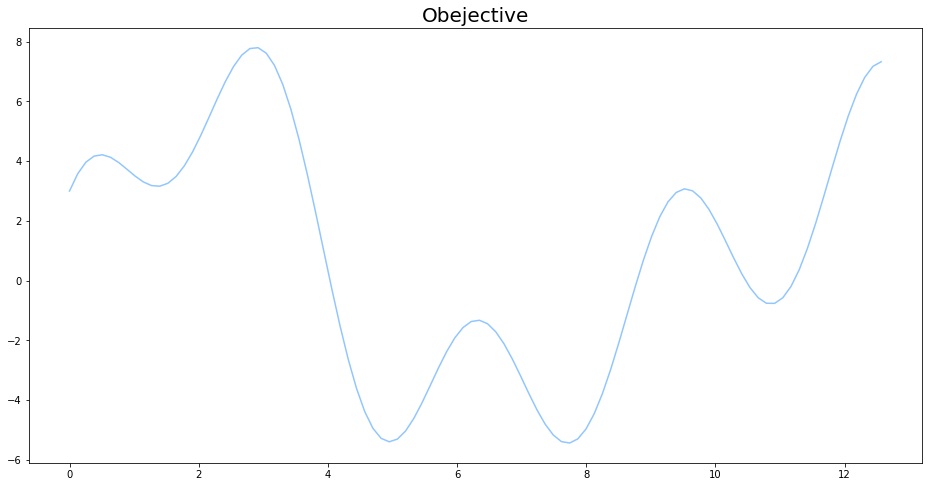
今回の記事で最大値を見つける目的関数は
f(x)=2\sin{(x)}+3\cos{(x)}+5\sin{(\frac{2}{3}x)} \\
0 \leq x \leq 4\pi
とします。説明の都合上、$f(x)$の具体的な形を与えていますが、一般的にはこの$f(x)$の形が分からなかったり、$f(x)$の値を求めるのに大きな計算コストがかかったりすることが多いです。
def objective(x):
return 2 * np.sin(x) + 3 * np.cos(2 * x) + 5 * np.sin(2 / 3 * x)
ベイズの定理
ベイズの定理は、事象の条件付き確率を計算する方法です。
P(A|B)=\frac{P(B|A) P(A)}{P(B)}
ベイズ最適化によって計算したいのは、条件付き確率そのものではなく関数の最大値であるので、ベイズの定理における正規化項を省略して分子のみ考えるだけで十分です。
P(A|B) \propto P(B|A) P(A)
上式で計算している$P(A|B)$は 事後確率(posterior) と呼ばれ、$P(B|A)$は 尤度関数(likelihood) 、$P(A)$は 事前確率(prior) と呼ばれます。
ベイズの定理は、black-boxな目的関数$f(x)$をサンプルリングされたデータに基づいて評価する上で強力なフレームワークです。
いくつかのデータ点$\mathbf{x}=(x_1,x_2,\dots,x_n)$に対して、その点における目的関数$f(x)$からのサンプリング$\mathbf{D}=(f(x_1),f(x_2),\dots,f(x_n))$を事前に保持していると仮定します。このサンプル点$\mathbf{x}$とデータ$\mathbf{D}$の対応が事前確率$P(f)$として解釈できます。
尤度関数$P(\mathbf{D}|f)$は目的関数$f(x)$によって観測できるデータの確率分布として解釈でき、データの数が増えるにつれて変化していきます。
事後確率$P(f|\mathbf{D})$は、正規化定数$P(\mathbf{D})$を考慮していないので目的関数そのものではないですが、得られたデータ$\mathbf{D}$に基づく目的関数の推定値と解釈できます。つまり、ベイズの定理における事後確率$P(f|\mathbf{D})$はベイズ最適化の代理関数と同じ意味合いを持ちます。
代理関数(Surrogate function)
代理関数は評価に大きな計算コストのかかる目的関数$f(x)$を計算コストをそこまでかけずに推定する関数です。
連続値を出力にもつ関数$f(x)$を最適化する場合は、代理関数には ガウス回帰(Gaussian Process Regression) が用いるのが一般的なようです。ただ、必ずしもガウス過程を用いる必要はなく、Random Forestなどのアルゴリズムも代理関数として採用されることもあります。
今回は一般的な例にならい、ガウス過程回帰を代理関数に用いてベイズ最適化の実装をおこなって行きます。
※注意
筆者は「ガウス過程と機械学習」を用いてガウス過程を勉強しました。基本的にここで述べる内容は「ガウス過程と機械学習」を簡単にまとめたものになります。
ガウス過程回帰(Gaussian Process Regression)
どんなN個の入力の集合$(\mathbf{x_{1}},\mathbf{x_{2}},\dots,\mathbf{x_{N}})$についても、対応する出力$({y_{1}},{y_{2}},\dots,{y_{N}})$の同時分布$p(\mathbf{y})$が多変量ガウス分布に従うとき、$\mathbf{X}$と$y$の関係は ガウス過程(Gaussian Process) に従うと言います。
\mathbf{y}\sim{N(\mathbf{0},\lambda^2\mathbf{\Phi}\mathbf{\Phi}^T)}
ガウス過程は,ある$\mathbf{x}$に対してスカラー$f(\mathbf{x})$を返すのではなく,$\mathbf{x}$における$f(\mathbf{x})$が従う正規分布の平均と分散を出力します。
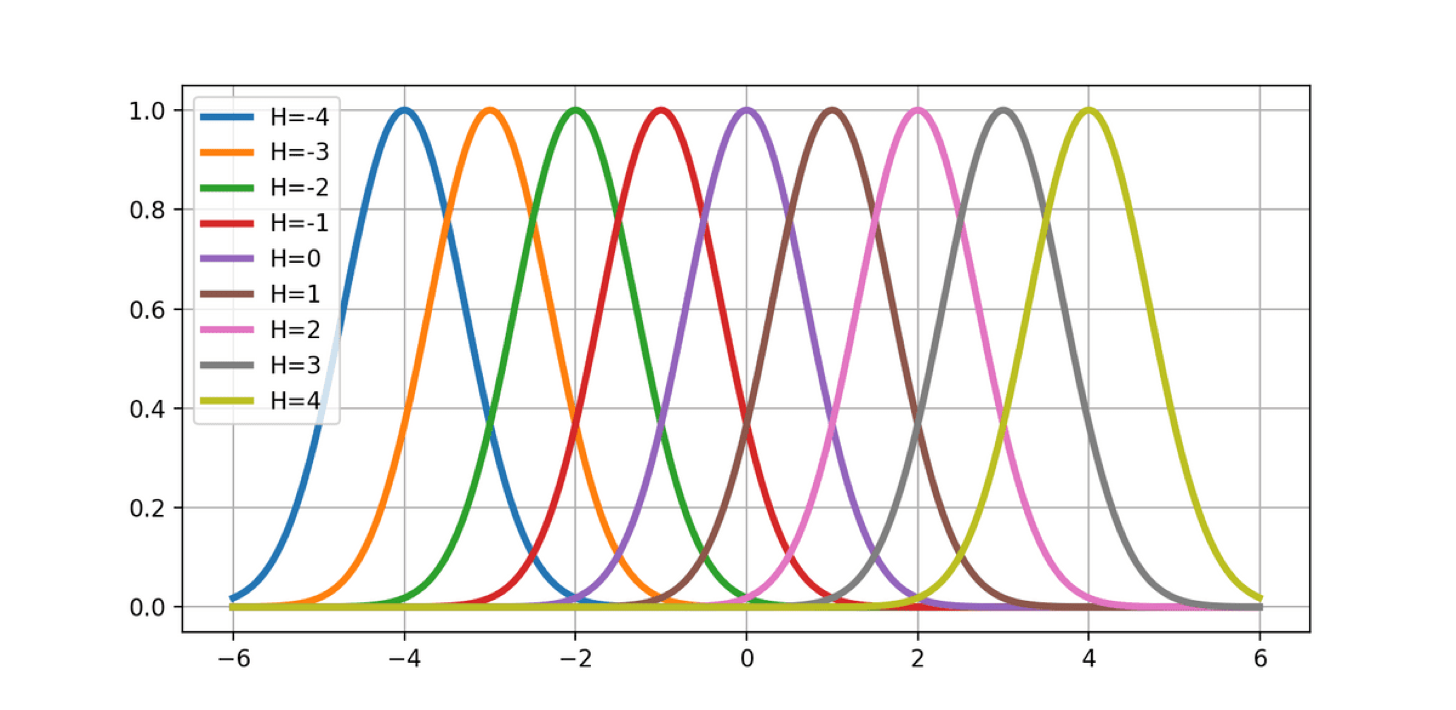
ガウス分布の形をした基底関数をグリッド状に配置して、適当に重み$w_i$で重みづけると、任意の形の関数が表すことができます。これを 動径基底関数回帰(Radial Basis Function Regression) と呼びます。
\phi_h(x)=\exp(-\frac{(x-u_h)^2}{\sigma^2})
y=\sum_{h=-H}^{H}w_h\phi{(x)}
しかしながら、動径基底関数回帰には問題点があります。例えば、グラフ上の-10~10の間にメモリ1毎に動径基底関数を配置していくと、$\mathbf{x}$が2次元なら441の動径基底関数が必要になり、$\mathbf{x}$が2次元なら441個の動径基底関数が必要になり、$\mathbf{x}$が5次元なら4084101個の動径基底関数が必要になります。
動径基底関数回帰では、次元の呪いによって$\mathbf{x}$の次元が大きくなるとすぐに、現実的な計算可能リソースを超えてしまうのです。
次元の呪いを解消する手段として、$\mathbf{w}$について期待値をとって、モデルから積分消去するというアイデアがあります。
\begin{pmatrix}\hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_N \end{pmatrix}=
\begin{pmatrix}
\phi_0(\mathbf{x_1}) & \phi_1(\mathbf{x_1}) & \dots & \phi_H(\mathbf{x_1}) \\
\phi_0(\mathbf{x_2}) & \phi_1(\mathbf{x_2}) & \dots & \phi_H(\mathbf{x_2}) \\
\vdots & \vdots & \ddots & \vdots \\
\phi_0(\mathbf{x_N}) & \phi_1(\mathbf{x_N}) & \dots & \phi_H(\mathbf{x_N})
\end{pmatrix}
\begin{pmatrix}w_0 \\ w_1 \\ \vdots \\ w_H \end{pmatrix}
\mathbf{\hat{y}}=\mathbf{\Phi}\mathbf{w}
重み$\mathbf{w}$が平均$\mathbf{0}$で分散$\lambda^2\mathbf{I}$のガウス分布
\mathbf{w}\sim{N(\mathbf{0},\lambda^2\mathbf{I})}
から生成されたものとします。
ガウス分布の性質より、ガウス分布に従うベクトルを線形変換したものもガウス分布に従うので、$\mathbf{y}$は平均$\mathbf{0}$で分散$\lambda^2\mathbf{\Phi}\mathbf{\Phi}^T$のガウス分布に従います。
E[\mathbf{y}]=E[\mathbf{\Phi}\mathbf{w}]=\mathbf{\Phi}E[\mathbf{w}]=\mathbf{0}
\begin{align}
\mathbf{\Sigma}&=E[\mathbf{y}\mathbf{y}^T]-E[\mathbf{y}]E[\mathbf{y}]^T=E[(\mathbf{\Phi}\mathbf{w})(\mathbf{\Phi}\mathbf{w})^T]\\
&=\mathbf{\Phi}E[\mathbf{w}\mathbf{w}^T]\mathbf{\Phi}^T=\lambda^2\mathbf{\Phi}\mathbf{\Phi}^T
\end{align}
このとき、$\mathbf{y}$の分布は$K_{n{n'}}=\lambda^2{\phi(\mathbf{x_n})\phi(\mathbf{x_{n'}})^T}$によって決まります。$k(\mathbf{x_n},\mathbf{x_{n'}})={\phi(\mathbf{x_n})^T\phi(\mathbf{x_{n'}})^T}$を カーネル関数(kernel) と呼び、データに応じて適切なカーネル関数選択することでガウス過程の性能が向上します。
カーネル関数の計算結果さえ分かれば回帰ができるので、$\phi(\mathbf{x})$を明示的に求める必要はありません。(カーネルトリック)
カーネル関数をプロットする関数を作ります。
def plot_kernel(kernel, title):
n = 100
x = np.linspace(-10, 10, n)
ys = []
for i in range(3):
mkernel = np.zeros((x.shape[0], x.shape[0]))
for i_row in range(x.shape[0]):
for i_col in range(i_row, x.shape[0]):
mkernel[i_row, i_col] = kernel(x[i_row], x[i_col])
mkernel[i_col, i_row] = mkernel[i_row, i_col]
K = 1**2 * np.dot(mkernel, mkernel.T)
y = np.random.multivariate_normal(np.zeros(len(x)), K)
ys.append(y)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
for y in ys:
ax.plot(x, y)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title(f'{title}')
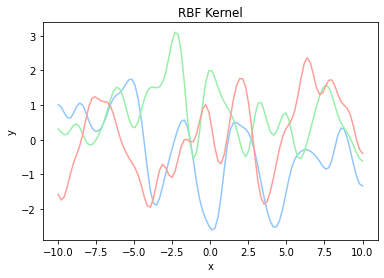
カーネルにはさまざまな種類があり、次に示す ガウスカーネル(Gaussian Kernel) などが一般的によく用いられます。$\theta_1$と$\theta_2$はハイパーパラメータであり、データに合わせて調整する必要があります。
k(\mathbf{x_n},\mathbf{x_{n'}})={\theta_1}\exp{(-\frac{|\mathbf{x}-\mathbf{x}'|}{\theta_2})}
ガウスカーネルの実装は数式をそのままプログラムに変換するだけで事足ります。
def rbf(x, x_prime, theta_1, theta_2):
return theta_1 * np.exp(-1 * (x - x_prime)**2 / theta_2)
plot_kernel(lambda x, x_prime: rbf(x, x_prime, 0.5, 0.5), 'RBF Kernel')
ガウスカーネルの他にも、 周期カーネル(Periodic Kernel) や 線形カーネル(Linear Kernel) 、 指数カーネル(Exponential Kernel) などがあります。
k(\mathbf{x_n},\mathbf{x_{n'}})=\exp{({\theta_1} \cos(\frac{|\mathbf{x}-\mathbf{x}'|}{\theta_2}))}
k(\mathbf{x_n},\mathbf{x_{n'}})= \mathbf{x_n}\mathbf{x_{n'}} + \theta
k(\mathbf{x_n},\mathbf{x_{n'}})= \exp{(-\frac{|\mathbf{x_n} - \mathbf{x_{n'}}|}{\theta})}
def periodic(x, x_prime, theta_1, theta_2):
return np.exp(theta_1 * np.cos((x - x_prime) /theta_2))
def linear(x, x_prime, theta):
return x * x_prime + theta
def exp(x, x_prime, theta):
return np.exp(-np.abs(x - x_prime) / theta)
plot_kernel(lambda x, x_prime: periodic(x, x_prime, 0.5, 0,5), 'Periodic Kernel')
plot_kernel(lambda x, x_prime: exp(x, x_prime, 0.5), 'Linear Kernel')
plot_kernel(lambda x, x_prime: exp(x, x_prime, 0.5), 'Exponential Kernel')
| 周期カーネル | 線形カーネル | 指数カーネル |
|---|---|---|
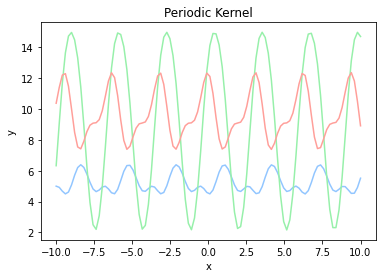 |
 |
 |
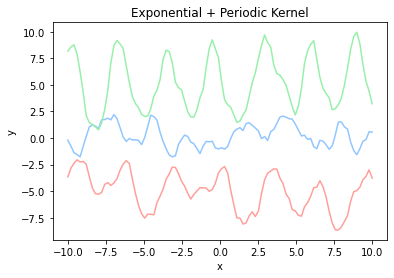
カーネルは複数を組み合わせて使うこともできます。株価などの周期性があり細かい変動が多いデータに対しては、指数カーネルで細かい変動を表し、周期カーネルで周期性を表すとを使うと、うまくフィッティングできそうな気がします。
kernel = lambda x, x_prime: 0.8 * exp(x, x_prime, 0.5) + 0.2 * periodic(x, x_prime, 0.5, 0.5)
plot_kernel(kernel, 'Exponential + Periodic Kernel')
データに含まれない$\mathbf{x*}$による$y*$の予測値は、$\mathbf{y}$に$y*$を含めた全体がまたガウス分布に従うことから
\begin{pmatrix}\mathbf{y} \\ y^{*} \end{pmatrix}{\sim}N(\mathbf{0},
\begin{pmatrix}
\mathbf{K} & \mathbf{k_*} \\
\mathbf{k_*^T} & k_{**}
\end{pmatrix}
)
とすることで、ガウス分布の性質を用いて計算することができます。
p(y^{*}{\mid}\mathbf{x^*}, D)=N(\mathbf{k_*^T}\mathbf{K}^{-1}\mathbf{y},k_{**}-\mathbf{k_*^T}\mathbf{K}^{-1}\mathbf{k})
D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),\dots,(\mathbf{x_N},y_N)\}
予測値が複数ある場合も同様にして計算ができます。
\begin{pmatrix}\mathbf{y} \\ y^{*}_1 \\ \vdots \\ y^{*}_M \end{pmatrix}{\sim}N(\mathbf{0},
\begin{pmatrix}
\mathbf{K} & \mathbf{k_*} \\
\mathbf{k_*^T} & \mathbf{k_{**}}
\end{pmatrix}
p(\mathbf{y^{*}}{\mid}\mathbf{x^*}, D)=N(\mathbf{k_*^T}\mathbf{K}^{-1}\mathbf{y},\mathbf{k_{**}}-\mathbf{k_*^T}\mathbf{K}^{-1}\mathbf{k})
ガウス過程回帰を実装していきます。
初めにデータを訓練用のデータとテスト用のデータに分割する関数を実装します。データ全体のうち、3割を訓練データ、残り7割をテストデータに分割します。
def train_test_split(x, y, test_size):
assert len(x) == len(y)
n_samples = len(x)
test_indices = np.sort(
np.random.choice(
np.arange(n), int(
n_samples * test_size), replace=False))
train_indices = np.ones(n_samples, dtype=bool)
train_indices[test_indices] = False
test_indices = ~ train_indices
return x[train_indices], x[test_indices], y[train_indices], y[test_indices]
n = 100
data_x = np.linspace(0, 4 * np.pi, n)
data_y = objective(data_x)
x_train, x_test, y_train, y_test = train_test_split(data_x, data_y, test_size=0.70)
次にガウス過程回帰の結果をプロットする関数を作成します。この関数は、目的関数、訓練データ点、ガウス過程回帰が返す平均と標準偏差をプロットします。
def plot_gpr(x_train, y_train, x_test, mu, var):
plt.figure(figsize=(16, 8))
plt.title('Gaussian Process Regressor', fontsize=20)
plt.plot(data_x, data_y, label='objective')
plt.plot(
x_train,
y_train,
'o',
label='train data')
std = np.sqrt(np.abs(var))
plt.plot(x_test, mu, label='mean')
plt.fill_between(
x_test,
mu + 2 * std,
mu - 2 * std,
alpha=.2,
label='standard deviation')
plt.legend(
loc='lower left',
fontsize=12)
plt.savefig('gpr.png')
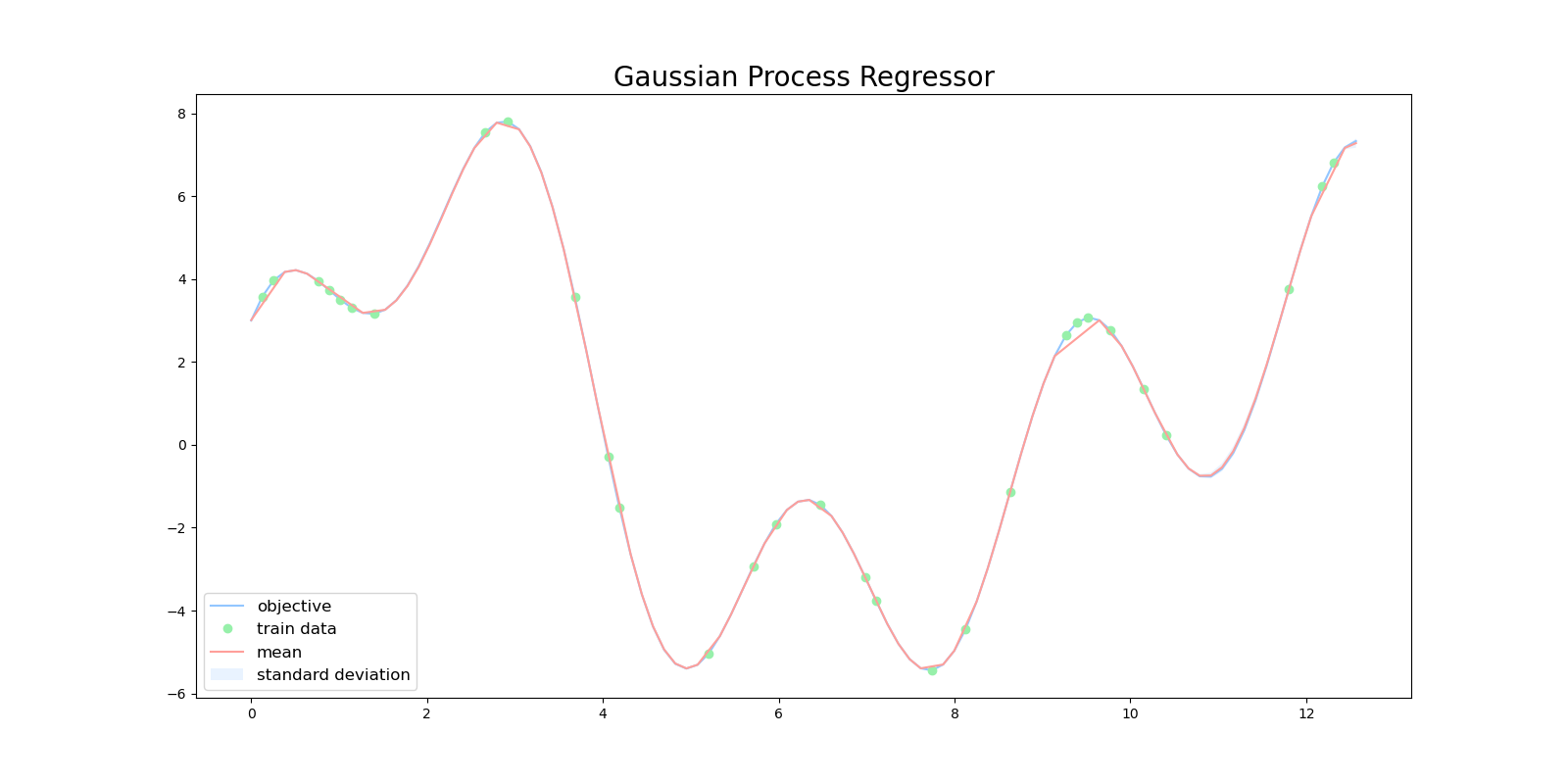
最後にガウス過程回帰を実装します。このプログラムでは、初めにカーネル行列$\mathbf{K}$を初期化し、訓練データを用いてカーネル行列$\mathbf{K}$を計算します。その後、それぞれのテストデータに対して、対応するカーネルを計算して、テストデータから回帰した平均と分散を出力します。
def gpr(x_train, y_train, x_test, kernel):
# average
mu = []
# variance
var = []
train_length = len(x_train)
test_length = len(x_test)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(x_train[x_idx], x_train[x_prime_idx])
yy = np.dot(np.linalg.inv(K), y_train)
for x_test_idx in range(test_length):
k = np.zeros((train_length,))
for x_idx in range(train_length):
k[x_idx] = kernel(
x_train[x_idx],
x_test[x_test_idx])
s = kernel(
x_test[x_test_idx],
x_test[x_test_idx])
mu.append(np.dot(k, yy))
kK_ = np.dot(k, np.linalg.inv(K))
var.append(s - np.dot(kK_, k.T))
return mu, var
# Radiant Basis Kernel
kernel = lambda x, x_prime : rbf(x, x_prime, theta_1=1.0, theta_2=1.0)
mu, var = gpr(x_train, y_train, x_test, kernel)
plot_gpr(x_train, y_train, x_test, mu, var)
ガウスカーネルを用いてガウス過程回帰を行ったところ、非常に精度良く回帰できました。これは目的関数が三角関数を重ね合わせた滑らかで複数の極値を持つ関数だったため、ガウスカーネルと相性が良かったためであると考えられます。
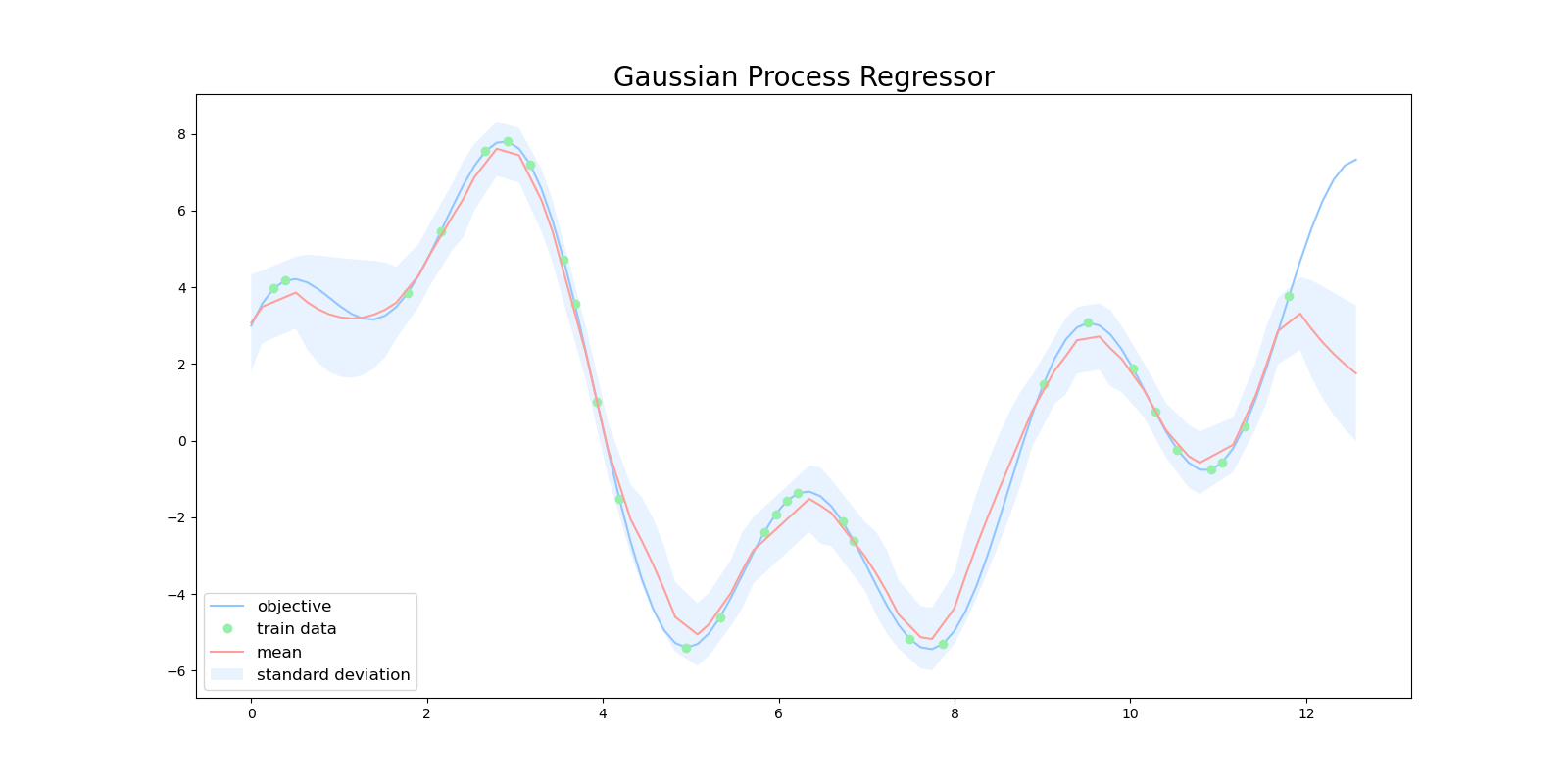
目的関数とカーネルの相性が悪いため、周期カーネルや線形カーネルではうまく回帰できませんでした。
| 周期カーネル | 線形カーネル |
|---|---|
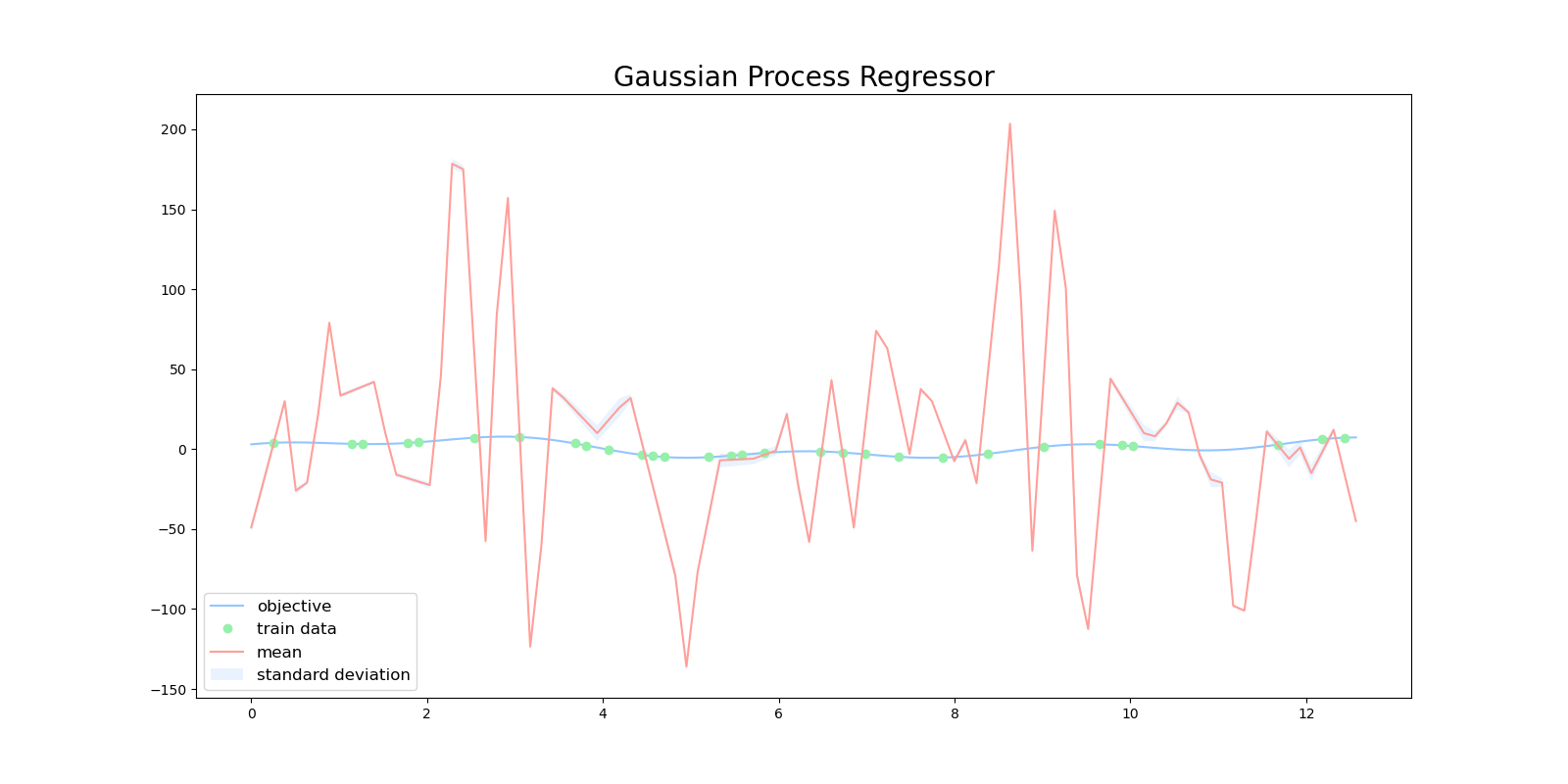 |
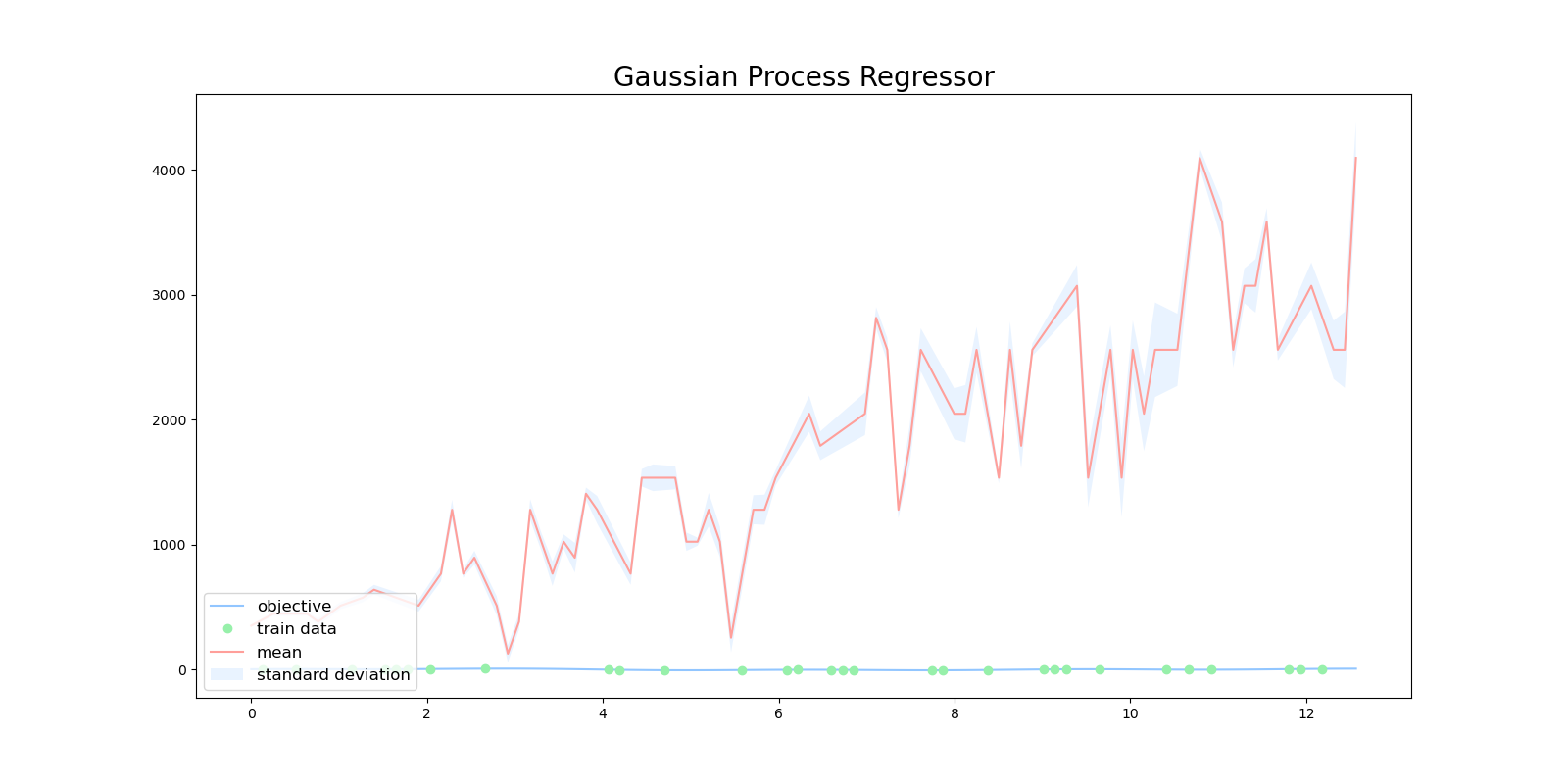 |
指数カーネルを用いるとガウスカーネルほどではないですが、ある程度の精度で回帰をできていました。しかしながら、信頼区間の幅がガウスカーネルに比べて大きく、ガウス過程が回帰結果に対して「自信がなさそう」と考えられます。
獲得関数(Acquisition function)
獲得関数は代理関数の出力に基づき次の探索点を決める関数です。
n個のデータ$\mathcal{D}_n$からガウス過程の出力として平均$\mathbf{\mu}$と分散$\mathbf{\sigma}^2$が分かっているとすると、獲得関数$a(x;\mathcal{D}_n)$を用いて
\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
x_{n+1}=\argmax_x a(x;\mathcal{D}_n)
とすることで、次の探索点を定めます。
獲得関数が満たすべき性質として、 探索(Exploration) と 活用(Exploitation) があります。
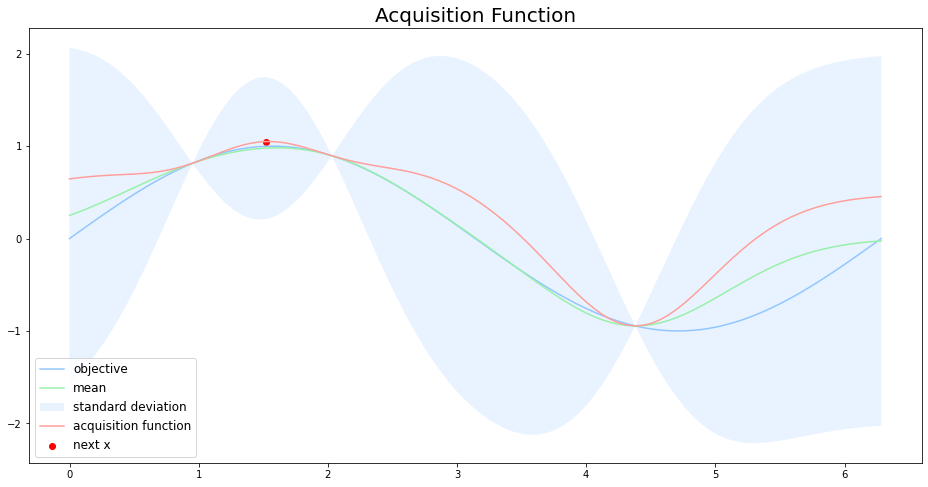
探索において、獲得関数は分散$\sigma^2$が大きいところを調べることで、目的関数$f(x)$の形状を調べます。下図において、水色の領域が信頼区間を表していて、獲得関数によって決まる次の探索点は、つ代理関数の信頼区間が大きく(分散$\sigma^2$が大きい)、最大値をとる可能性が高いところになっています。
活用において、獲得関数は平均$\mu$の値が大きいところを調べることで、目的関数$f(x)$の最大値を当てにいきます。下図において、獲得関数によって決まる次の探索点は、代理関数の平均値の値が大きい点になっています。
したがって、初めのうちは探索を行い関数の形を調べ、関数の形が分かってきたら活用によって最適値を当てにいくのが、理想的な獲得関数の性質となります。
一般的に有名な獲得関数として、 信頼性上限(Upper Confidence Bound) 、 改善確率(Probability of Improvement)、 期待改善度(Expected Improvement) があります。
信頼性上限(Upper Confidence Bound)
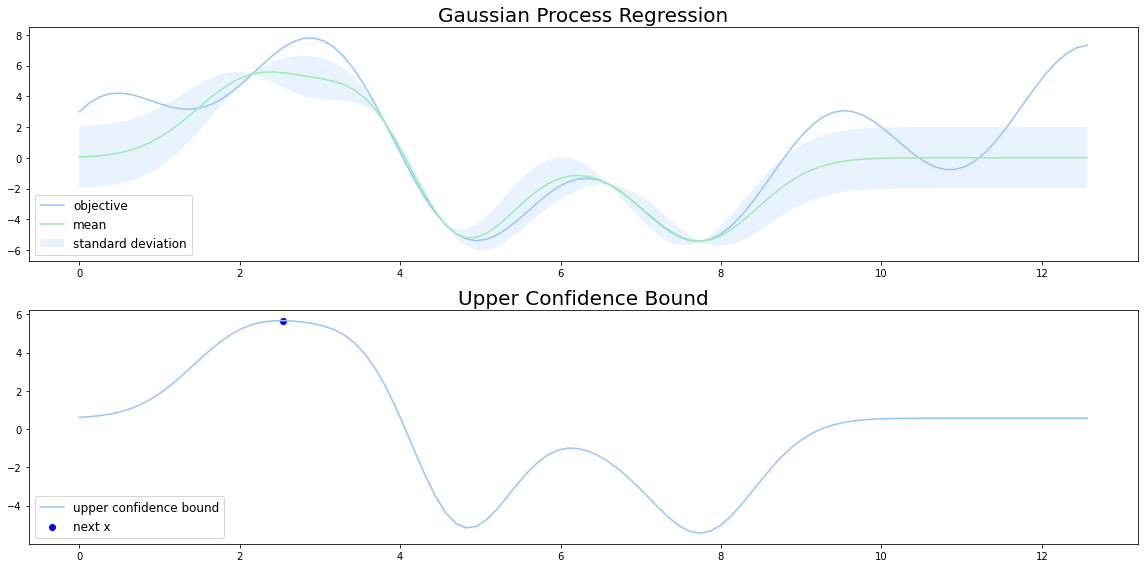
UCBは代理関数の 信頼区間で最大値を取る点を 次の探索点とする方法です。
a_{UCB}(\mathbf{x};\mathcal{D}_n)=\mu + k\sigma
下図においては、$x=2$付近のとき、平均と信頼区間の和が最大値をとっているので、この点が次の探索点になります。
kの値はハイパーパラメータで、
k=\sqrt{\frac{\log{n}}{n}}
などが用いられるようです。この$k$では、探索回数$n$が小さいときは探索を中心に行い、探索回数$n$が大きくなるにつれては徐々に活用を中心に行ないます。trialは現在のサンプル回数を渡す引数です。
def UCB(mu, var, trial):
k = np.sqrt(np.log(trial) / trial)
return mu + k * var
改善確率(Probability of Improvement)
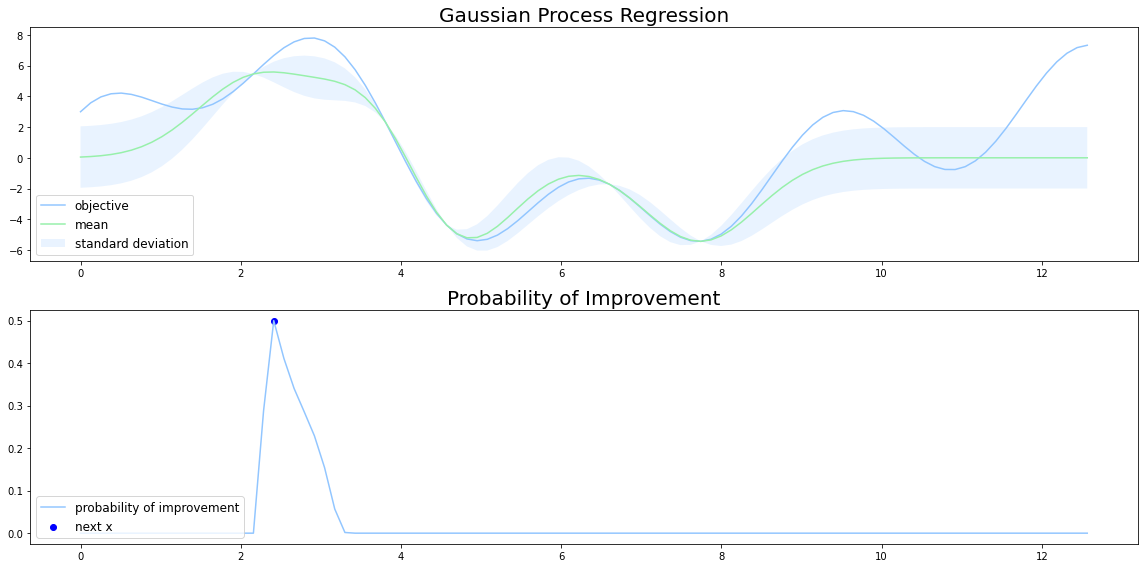
改善確率は現状での最適解よりもさらによい解となる確率を 獲得関数とする方法です。したがって、改善確率では現状で得られている最適解の 周辺を重点的に調べるという性質があります。
a_{PI}(\mathbf{x};\mathcal{D}_n)=P[y>\hat{y}]
代理関数がガウス過程の場合など、$y$が正規分布$\mathcal{N}(y|\mu,\sigma^2)$にしたがっているとき、改善確率$a_{PI}(\mathbf{x};\mathcal{D}_n)$は次の式で表されます。
a_{PI}(\mathbf{x};\mathcal{D}_n)=\Phi(\frac{\mu-\hat{y}}{\sigma})
\Phi(x)=\int_{-\infty}^{x}\mathcal{N}(x|0,1)dx
改善確率は不確実だが大きく改善するかもしれない点 よりも、 改善量は小さいが確実に改善する点を調べる傾向にあるため、局所的な解に陥りやすいという問題点があります。
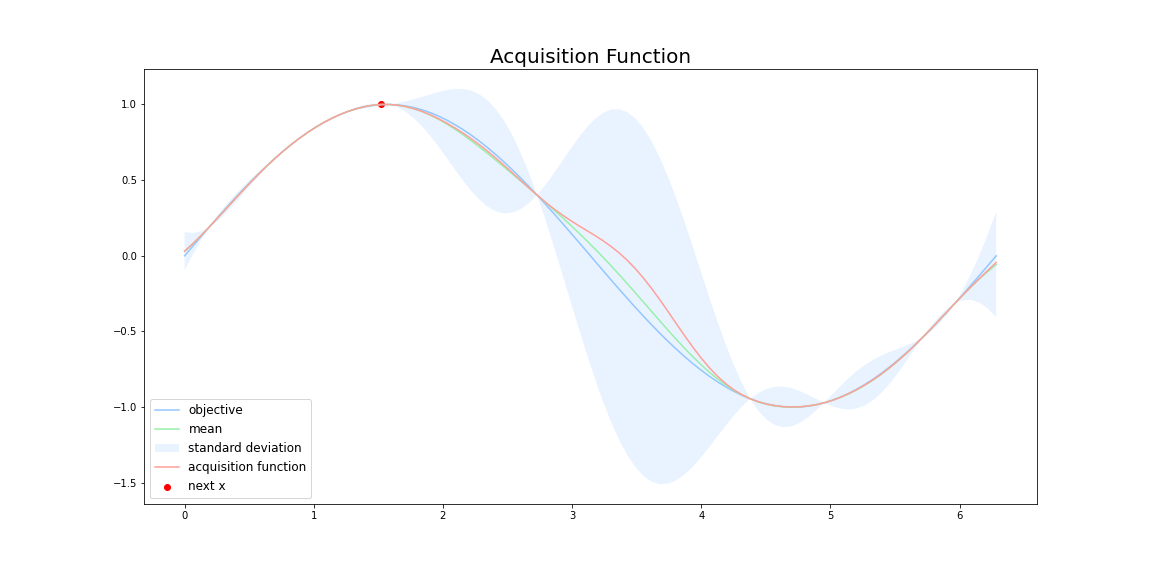
獲得関数の形状がUCBとは大きく違い、改善確率ではある一点で尖った形になっています。
改善確率の実装は次のようになります。epsは分散が0のとき、thetaの値がinfになるのを防ぐために入れています。
from scipy.stats import norm
def PI(mean,var):
eps = 1e-7
y_hat = np.max(mu)
theta = (mean - y_hat)/(var + eps)
return np.array([norm.cdf(theta[i]) for i in range(len(theta))])
期待改善度(Expected Improvement)
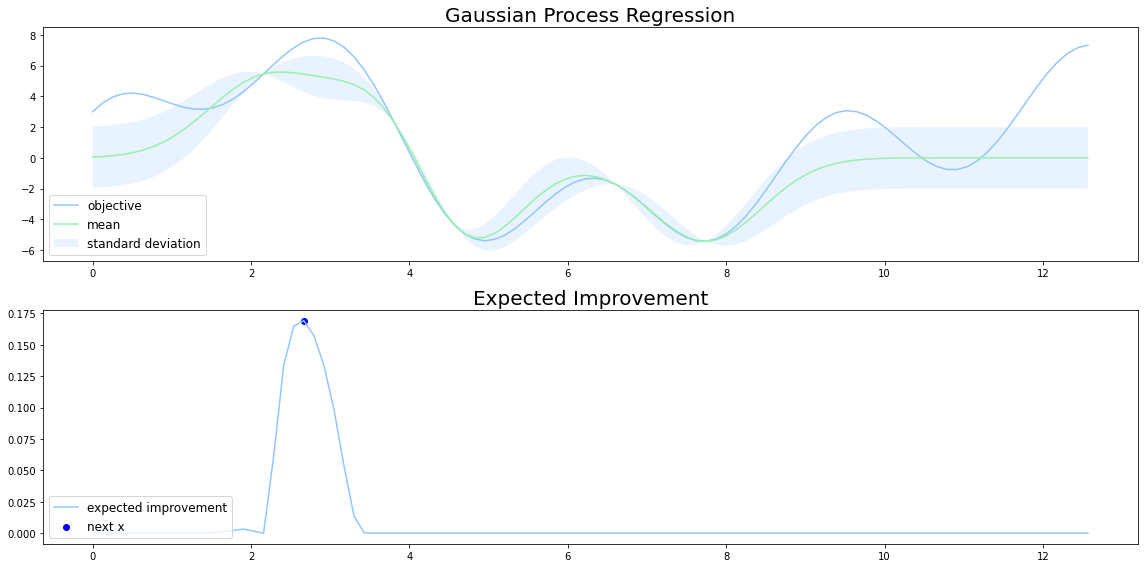
期待改善度は現状での最適解との出力の 差分の期待値 を獲得関数とする方法です。
a_{EI}(\mathbf{x};\mathcal{D}_n)=E[\max\{{y-\hat{y},0}\}]
詳しい証明はこちらの記事が参考になりそうでした。
$y$が正規分布$\mathcal{N}(y|\mu,\sigma^2)$にしたがっているとき、期待改善度$a_{EI}(\mathbf{x};\mathcal{D}_n)$は次の式で表されます。
a_{EI}(\mathbf{x};\mathcal{D}_n)=\sigma\times(\frac{\mu-\hat{y}}{\sigma}\Phi(\frac{\mu-\hat{y}}{\sigma})+\phi(\frac{\mu-\hat{y}}{\sigma}))
\Phi(x)=\int_{-\infty}^{x}\mathcal{N}(x|0,1)dx
\phi(x)=\sqrt{\frac{1}{2\pi}}\exp{(-\frac{1}{2}x^2)}
期待改善度${a_{EI}(\mathbf{x};\mathcal{D}_n)}$では、分散が大きくなるほど期待改善度が大きくなるため、改善確率とは異なり探索と活用をバランスよく行うことができます。
改善確率と期待改善度の形状の違いは、改善確率が次の探索点において「尖っている」のに対して、期待改善度では丸みを帯びた「滑らか」な形をしています。これは改善確率とは異なり、探索にも重きをおいている期待改善度の性質によるものです。
from scipy.stats import norm
def EI(mu,var):
eps = 1e-7
sigma = np.sqrt(np.abs(var))
y_hat = np.max(mu)
theta = (mu - y_hat)/(sigma + eps)
return np.array([(mu[i] - y_hat)*norm.cdf(theta[i]) + sigma[i]*norm.pdf(theta[i]) for i in range(len(theta))])
ベイズ最適化
紹介した代理関数、獲得関数を用いてベイズ最適化のプログラムを実装します。基本的に代理関数と獲得関数の性質さえ理解できていれば、ベイズ最適化のプログラム自体はそこまで難しくないと思います。
最初に触れた通り、ベイズ最適化は以下の操作を繰り返すことで探索を行い、最大値を見つけます。
- 事前に目的関数$f(x)$からいくつかのサンプルをサンプリングしておく
- 保持しているサンプルを用いて代理関数を計算する
- 代理関数の出力を用いて獲得関数を計算し次の探索点を決める
- 目的関数$f(x)$から獲得関数で決めた探索点をサンプリングする
- 新しいサンプルに既存のサンプルを追加する
- 2~5を繰り返す
n_trials = 15
n = 10000
data_x = np.linspace(0, 4 * np.pi, n)
data_y = objective(data_x)
x_train, x_test, y_train, y_test = train_test_split(
data_x, data_y, test_size=0.9997)
# RBF Kernel
def kernel(x, x_prime):
return rbf(x, x_prime, theta_1=1.0, theta_2=1.0)
# Upper Confidence Bound
def UCB(mu, var):
k = 20.0
return mu + k * var
def plot_bo(mu, var, trial, x_new, y_new):
plt.figure(figsize=(24, 8))
plt.title('Bayesian Optimization', fontsize=20)
plt.ylim(-6, 10)
plt.plot(data_x, data_y, label='objective')
std = np.sqrt(np.abs(var))
plt.plot(data_x, mu, label='mean')
plt.fill_between(
data_x,
mu + 2 * std,
mu - 2 * std,
color='turquoise',
alpha=.2,
label='standard deviation')
plt.scatter(x_new, y_new, color='blue', label='next x')
plt.legend(
loc='lower left',
fontsize=12)
plt.savefig(f'bo_{trial}.png')
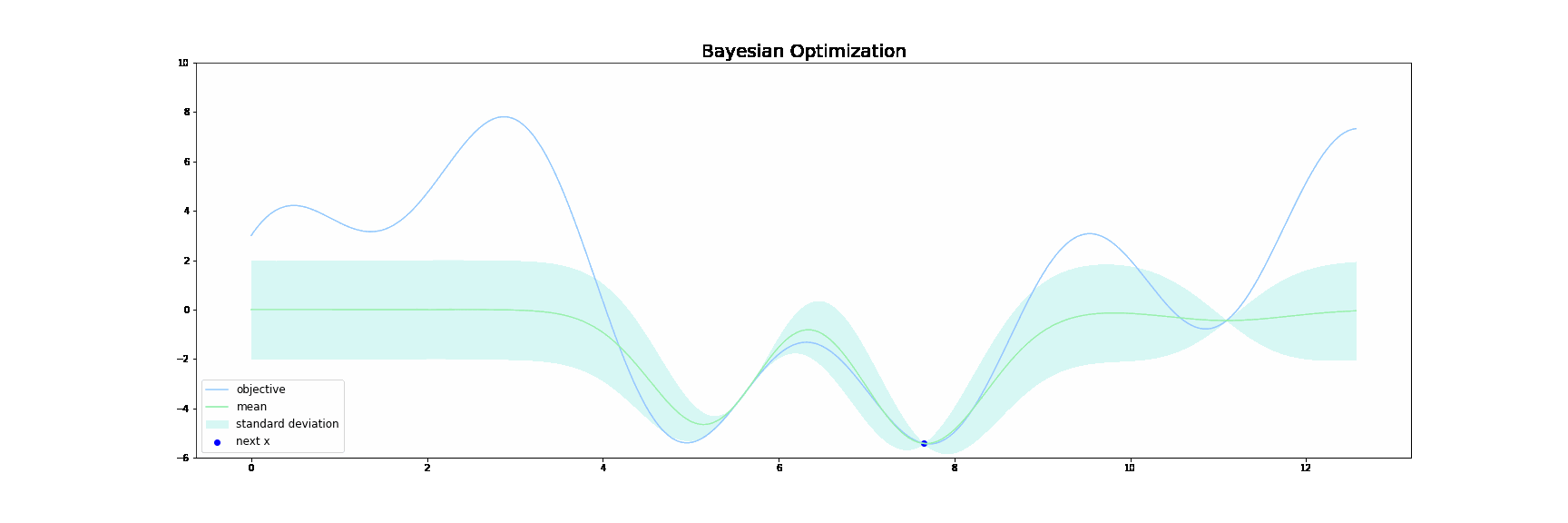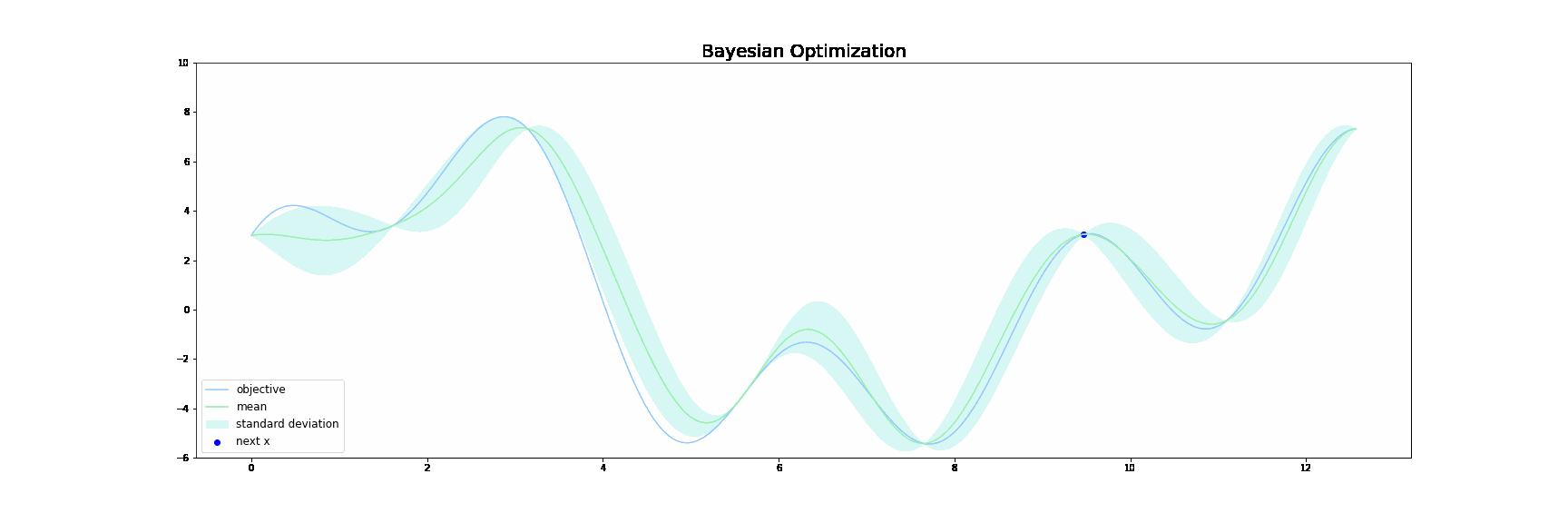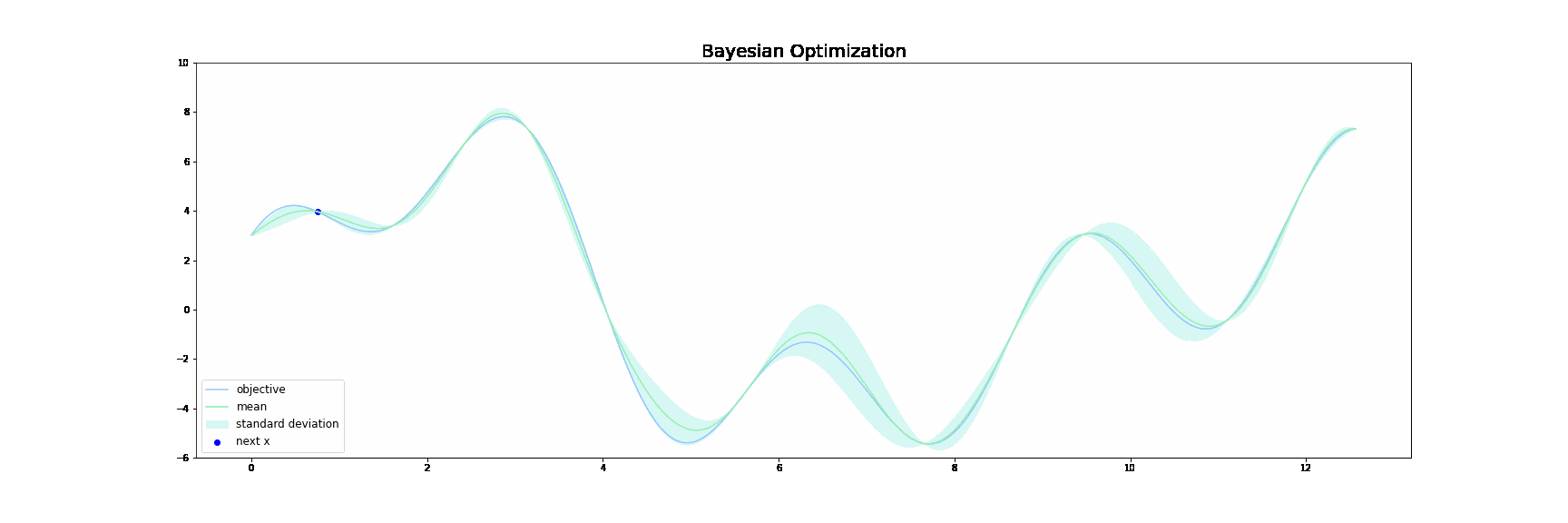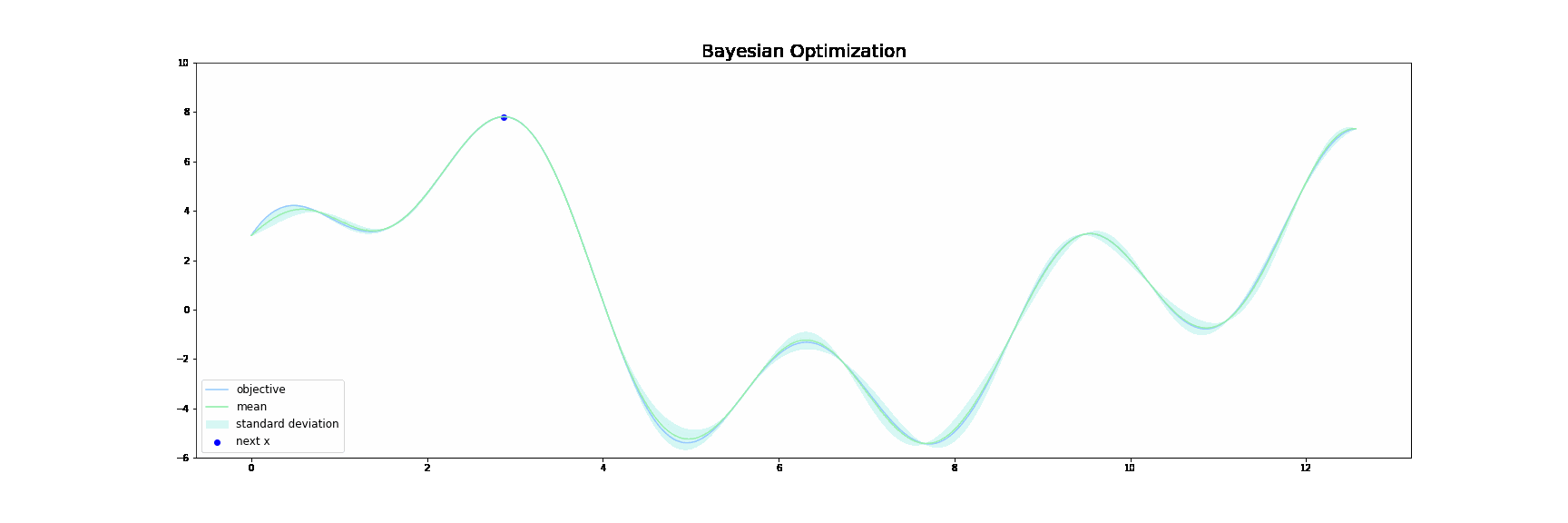
def bayes_opt(x_train, y_train, data_x, objective, n_trials, kernel):
mu, var = gpr(x_train, y_train, data_x, kernel)
for trial in range(n_trials):
ucb = UCB(mu, var)
arg_max = np.argmax(ucb)
x_new = data_x[arg_max]
y_new = objective(data_x[arg_max])
if(x_new not in x_train):
x_train = np.hstack([x_train, x_new])
y_train = np.hstack([y_train, y_new])
mu, var = gpr(x_train, y_train, data_x, kernel)
plot_bo(mu, var, trial, x_new, y_new)
bayes_opt(x_train, y_train, data_x, objective, n_trials, kernel)
カーネルにはガウスカーネルを、獲得関数にはUCBを用いました。ベイズ最適化の様子をプロットすると下図のようになります。探索を始めて、複数あるの極大値に囚われることなく、大域的な最大値を見つけることに成功しています。
獲得関数に関してですが、UBCで$k=20$にすることで探索寄りに変更してあります。理由は、目的関数の形が比較的単純で探索範囲が小さいため、ガウス過程が返す分散の値が小さくなる傾向にあるためです。
獲得関数の選択はこうするべきといったものはなく、時と場合によることが多いです。今回用いた獲得関数は、序盤は探索を中心に行い最終的に活用をして最大値を見つけることができているので、理想的な獲得関数だといえると思います。
まとめ
ベイズ最適化のプログラムをゼロから自分の手で実装してみました。
個人的には新しい情報系の理論を勉強するときは、プログラムをゼロから自分の手で実装してみる派ですが、試行錯誤をしていると感覚的なところもベイズ最適化への理解が深まりました。
ここまで読んでいただきありがとうございます。
今回実装したコードは全てこちらのレポジトリにあります。
参考
[1] Jasper Snoek, Hugo Larochelle, and Ryan P. Adams. Practical Bayesian Optimization of Machine
Learning Algorithms. 2012.
[2] Jasper Snoek, Hugo Larochelle, and Ryan P. Adams. A Tutorial on Bayesian Optimization of
Expensive Cost Functions, with Application to
Active User Modeling and Hierarchical
Reinforcement Learning. 2010.
[3] Bobak Shahriari, Kevin Swersky, Ziyu Wang, Ryan P. Adams and Nando de Freitas. Taking the Human Out of the Loop: A Review of Bayesian Optimization. 2016.
[4] ベイズ最適化入門
[5] ガウス過程と機械学習
[6]シンプルなベイズ最適化について