前回執筆した「ガウス過程 from Scratch」では、 ガウス過程(Gaussian Process) をゼロから実装することで、ガウス過程への理解を深めました。
前回の記事では回帰を行うときにカーネルのハイパーパラメータをあらかじめ良い値に設定してありました。しかしながら、ガウス過程を実際用いる場合には最適なハイパーパラメータは事前にわからない状態であることがほとんどです。
今回の記事では、ガウス過程のハイパーパラメータ最適化を実行するプログラムをゼロから実装することで、背景にある数学的な理論を理解することを目的とします。
一般的にガウス過程のハイパーパラメータ最適化の文脈で用いられるのは、 マルコフ連鎖モンテカルロ法(Markov chain Monte Carlo method、以下MCMC) か 勾配法(Gradient Decent method) です。この記事では、MCMCと勾配法の両方の実装を行なっていきます。
※注意
この記事は筆者が勉強したことをまとめて、理解を深めるために執筆しています。内容に誤り等があった場合は、コメント等でご指摘いただけると幸いです。
ガウス過程(Gaussian Process)
どんなN個の入力の集合 $(\mathbf{x_{1}},\mathbf{x_{2}},\dots,\mathbf{x_{N}})$ についても、対応する出力 $(f(\mathbf{x_{1}}),f(\mathbf{x_{2}}),\dots,f(\mathbf{x_{N}}))$ の同時分布 $p(\mathbf{f})$ が、平均 $\mathbf{u}$ と $K_{n{n'}}=k(\mathbf{x_n},\mathbf{x_{n'}})$ を要素とする共分散行列 $\mathbf{K}$ のガウス分布 $\mathbb{N}(\mathbf{u},\mathbf{K})$ に従うとき、 $\mathbf{f}$ は ガウス過程(Gaussian Process) に従うと言います。
\mathbf{f}\sim \textrm{GP}(\mathbf{u},k(\mathbf{x},\mathbf{x'}))
ガウス過程は,ある$\mathbf{x}$に対してスカラー$f(\mathbf{x})$を返すのではなく,$\mathbf{x}$における$f(\mathbf{x})$が従う正規分布の平均と分散を出力します。
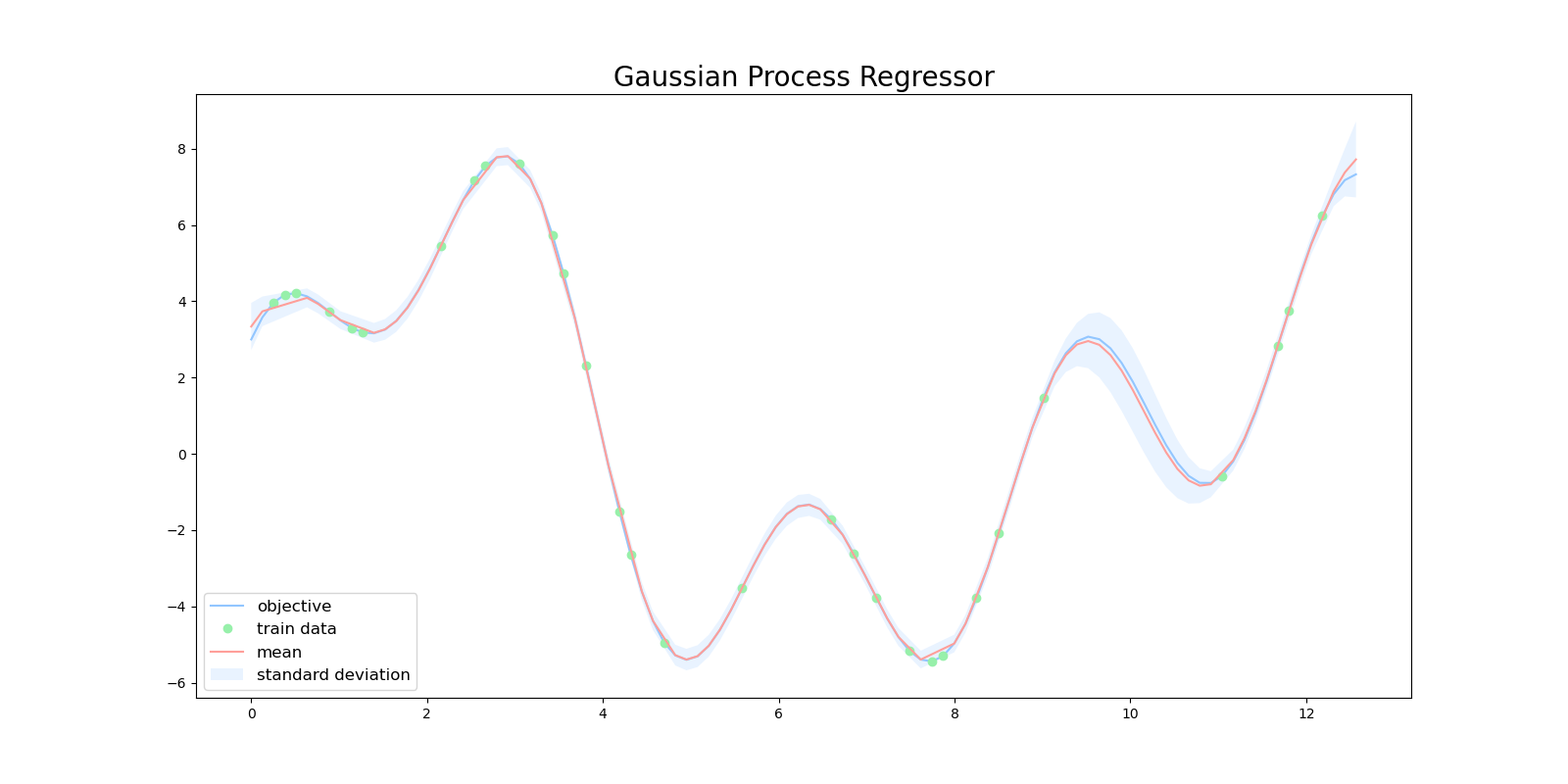
したがって、ガウス過程ではある予測に対する信頼度を表現することができます。下図は、ガウス過程を用いて目的関数を回帰した図になります。緑色の点が学習用データで、赤い線が平均値、水色の領域は全体の95%の信頼区間を表しています。
$x=10$ 周辺に注目すると、この区間では訓練データが少ないため、ガウス過程の出力も自信がない(分散が大きい)ものになっています。
一般的に観測する $y$ にはノイズがのっていることが多いので、
y = f(\mathbf{x})+\epsilon
\epsilon\sim \mathbb{N}(0,\sigma^2)
とするのが自然です。
ノイズを考慮した上でのガウス過程は、 $K_{n{n'}}=k(\mathbf{x_n},\mathbf{x_{n'}})$ を要素とする共分散行列 $\mathbf{K}$ の対角成分に、 $\sigma^2$ を足したものとして表現できます。
k'(\mathbf{x_n},\mathbf{x_{n'}})=k(\mathbf{x_n},\mathbf{x_{n'}})+\sigma^2\delta(n,n')
詳しい解説は前回の記事を参照してください。
イントロダクション
今回の実験で用いる目的関数を次のように設定します。
f(x)=2\sin{(x)}+3\cos{(x)}+5\sin{(\frac{2}{3}x)} \\
0 \leq x \leq 4\pi
はじめに、基本的なカーネルである ガウスカーネル(Gaussian Kernel) を用いてガウス過程回帰を行います。
k(\mathbf{x_n},\mathbf{x_{n'}})={\theta_1}\exp{(-\frac{|\mathbf{x}-\mathbf{x}'|}{\theta_2})}
前述の通り、観測にはノイズが乗っていることを想定し最終的なカーネル関数は次の通りです。
k(\mathbf{x_n},\mathbf{x_{n'}})={\theta_1}\exp{(-\frac{|\mathbf{x}-\mathbf{x}'|}{\theta_2})} + \theta_3\delta(n, n')
$\delta(n, n')$ はデルタ関数で、 $n=n'$ のときに$1$をそれ以外のときは$0$を返します。したがって、このカーネル関数には $(\theta_1,\theta_2,\theta_3)$ の3つのハイパーパラメータが存在します。次に示すプログラムでは $(\theta_1,\theta_2,\theta_3)=(0.5, 0.5, 0.5)$ という筆者がランダムに選んだ値を設定します。
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-pastel')
def rbf(x, x_prime, theta_1, theta_2):
"""RBF Kernel
Args:
x (float): data
x_prime (float): data
theta_1 (float): hyper parameter
theta_2 (float): hyper parameter
"""
return theta_1 * np.exp(-1 * (x - x_prime)**2 / theta_2)
def objective(x):
return 2 * np.sin(x) + 3 * np.cos(2 * x) + 5 * np.sin(2 / 3 * x)
def train_test_split(x, y, test_size):
assert len(x) == len(y)
n_samples = len(x)
test_indices = np.sort(
np.random.choice(
np.arange(n_samples), int(
n_samples * test_size), replace=False))
train_indices = np.ones(n_samples, dtype=bool)
train_indices[test_indices] = False
test_indices = ~ train_indices
return x[train_indices], x[test_indices], y[train_indices], y[test_indices]
n = 100
data_x = np.linspace(0, 4 * np.pi, n)
data_y = objective(data_x)
x_train, x_test, y_train, y_test = train_test_split(
data_x, data_y, test_size=0.70)
def plot_gpr(x_train, y_train, x_test, mu, var):
plt.figure(figsize=(16, 8))
plt.title('Gaussian Process Regressor', fontsize=20)
plt.plot(data_x, data_y, label='objective')
plt.plot(
x_train,
y_train,
'o',
label='train data')
std = np.sqrt(np.abs(var))
plt.plot(x_test, mu, label='mean')
plt.fill_between(
x_test,
mu + 2 * std,
mu - 2 * std,
alpha=.2,
label='standard deviation')
plt.legend(
loc='lower left',
fontsize=12)
plt.savefig('gpr.png')
def gpr(x_train, y_train, x_test, kernel):
# average
mu = []
# variance
var = []
train_length = len(x_train)
test_length = len(x_test)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], x_idx == x_prime_idx)
yy = np.dot(np.linalg.inv(K), y_train)
for x_test_idx in range(test_length):
k = np.zeros((train_length,))
for x_idx in range(train_length):
k[x_idx] = kernel(
x_train[x_idx],
x_test[x_test_idx],
x_idx == x_test_idx)
s = kernel(
x_test[x_test_idx],
x_test[x_test_idx],
x_test_idx == x_test_idx)
mu.append(np.dot(k, yy))
kK_ = np.dot(k, np.linalg.inv(K))
var.append(s - np.dot(kK_, k.T))
return np.array(mu), np.array(var)
if __name__ == "__main__":
# Radiant Basis Kernel + Error
def kernel(x, x_prime, noise, theta_1=0.5, theta_2=0.5, theta_3=0.5):
# delta function
if noise:
delta = theta_3
else:
delta = 0
return rbf(x, x_prime, theta_1=theta_1, theta_2=theta_2) + delta
mu, var = gpr(x_train, y_train, x_test, kernel)
plot_gpr(x_train, y_train, x_test, mu, var)
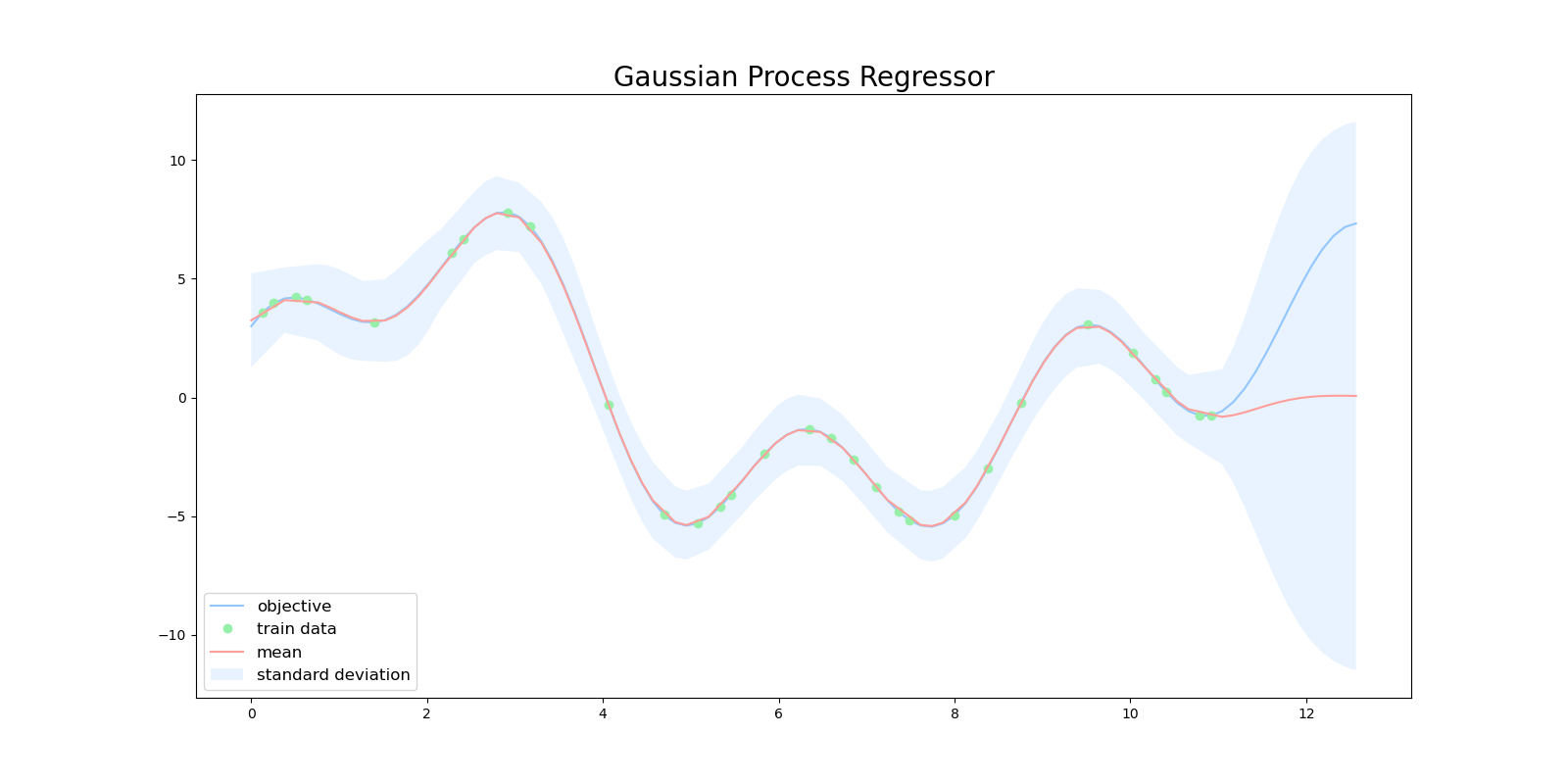
このプログラムを実行すると次のような結果が得られます。目的関数(青線)に対し、回帰の結果(赤線)がうまくフィットできていません。
この記事では上記のプログラムに、ハイパーパラメータを最適化するプログラムを追加していくことで、回帰の精度を向上させていきます。
MCMCによる最適化
マルコフ連鎖モンテカルロ法(Markov chain Monte Calro method)
一般的なベイズの定理は以下の式で表されます。$\theta$が推定したいパラメータで、$D$が推定に用いることができるデータです。
\begin{aligned}
p\left(\theta | D\right) &=\frac{p\left(D| \theta\right)p(\theta)}{\int p\left(D| \theta\right)p(\theta) d \theta}
\end{aligned}
この計算では、右辺の分母のようにパラメータの積分計算が必要となりますが、しばしばこの積分計算自体が困難な場合があります。右辺の分母を正規化定数と呼びます。
正規化定数を解析的に求めずに事後分布からサンプリングしたい場合に、 マルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods,以下MCMC法) は有効な手段となります。
MCMC法は、「マルコフ連鎖」と「モンテカルロ法」の組み合わせです。「マルコフ連鎖」や「モンテカルロ法」の理解が怪しい方は、こちらの記事などを参照してください。
確率変数の系列$\mathbf{z}^{(1)},\mathbf{z}^{(2)},\dots$に対して
p(\mathbf{z}^{(t)}|\mathbf{z}^{(1)},\mathbf{z}^{(2)},\dots,\mathbf{z}^{(t-1)})=p(\mathbf{z}^{(t)}|\mathbf{z}^{(t-1)})
が成り立つとき、系列$\mathbf{z}^{(1)},\mathbf{z}^{(2)},\dots$を 一次マルコフ連鎖(first-order Markov Chain) と呼び、$p(\mathbf{z}^{(t)}|\mathbf{z}^{(t-1)})$を 遷移確率 と呼びます。
次式が成り立つとき、分布$p_{*}(\mathbf{z})$は 定常分布 であるといいます。数式の直感的な意味としては、遷移確率に従って事後分布の更新を十分に繰り返したあとに、もう一度遷移確率に従って事後分布を更新しても、分布の様子は変わらない(定常状態)という感じです。
p_{*}(\mathbf{z}) = \int p(\mathbf{z}'|\mathbf{z}) p_{*}(\mathbf{z}') d\mathbf{z}'
定常分布$p_{*}(\mathbf{z})$がサンプルを取り出したい事後分布であるとして、$p(\mathbf{z})$に分布収束するような遷移確率$p(\mathbf{z}^{(t)}|\mathbf{z}^{(t-1)})$を設計するのがMCMC法のアイデアです。
$p_{*}(\mathbf{z})$が定常分布となるための十分条件として、 詳細釣り合い条件(detailed balance condition) があります。
p(\mathbf{z}'|\mathbf{z})p_{*}(\mathbf{z}) = p(\mathbf{z}|\mathbf{z}')p_{*}(\mathbf{z}')
MCMC法が効果を発揮するための数学的な条件としては、詳細釣り合い条件に加えて、サンプルサイズを大きくしたときに遷移確率$p(\mathbf{z}^{(t)}|\mathbf{z}^{(t-1)})$によって任意の初期状態から定常状態$p_{*}(\mathbf{z})$に収束することも必要です。この特性を エルゴード性(ergodicity) と呼びます。
エルゴード性(ergodicity)
- 規約性(irreducible)
- 任意の状態から任意の状態へ有限回数で遷移できること
- 非周期性(aperiodic)
- 全ての状態が周期性を持たないこと
- 正再帰性(positive )
- 全ての状態に有限回で戻ることができること
メトロポリス・ヘイスティング法(Metropolis-Hastings method)
MCMC法の最も基本的な手法として、 メトロポリス・ヘイスティングス法(Metropolis-Hastings method,以下M-H法) があります。ベイズの定理において、$\int p\left(D| \theta\right)p(\theta) d \theta$が計算できず、$p\left(D| \theta\right)p(\theta)$が計算可能な場合を想定し、事後分布$p\left(\theta | D\right)$を求めていきます。
\begin{aligned}
p\left(\theta | D\right) &=\frac{p\left(D| \theta\right)p(\theta)}{\int p\left(D| \theta\right)p(\theta) d \theta}
\end{aligned}
MCMC法において、定常分布に収束させるための遷移確率が必要となりますが、遷移確率を直接設計せずに遷移の提案分布$q(\mathbf{z}|\mathbf{z}')$を用います。
重要なのは、サンプリングを試みたい定常分布から直接サンプリングは難しいけれども、提案分布からなら容易にサンプリングが可能という点です。ここで、提案分布により得られた$q(\mathbf{z}|\mathbf{z}')$をの確率で採択することで、詳細つり合い条件を満たすように 棄却サンプリング(rejection sampling) を行おうというのがM-H法のアイデアです。
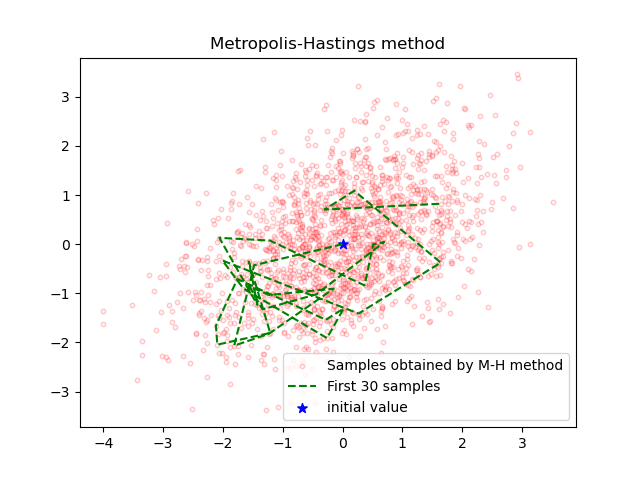
MCMC法の例として2次元のガウス分布からサンプリングしてみます。
\mathbf{N}(\boldsymbol{x} | \mu, \Sigma)=\frac{1}{\sqrt{(2 \pi)^{D}|\Sigma|}} \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}
u=0
\begin{aligned}
\Sigma^{-1}=\left(\begin{array}{cc}
{1} & {-a} \\
{-a} & {1}
\end{array}\right)
\end{aligned}
今回の例では2次元のガウス分布は解析的に求めることができるので、目標分布から直接サンプリングすることが可能ですが、通常MCMC法は分布が解析的に求められない場合に用いられます。
import copy
import numpy as np
import matplotlib.pyplot as plt
a = 0.5
# P(z1, z2) is target distribution without regulization term.
def P(z1, z2):
return np.exp(-0.5 * (z1**2 - 2 * a * z1 * z2 + z2**2))
# Q(x) : Proposal distribution
def Q(c, mu1, mu2, sigma):
return (
c[0] +
np.random.normal(
mu1,
sigma),
c[1] +
np.random.normal(
mu2,
sigma))
def metropolis(N, mu1, mu2, sigma):
z = (0, 0)
sample = []
sample.append(z)
accept = []
for i in range(N):
z_new = Q(z, mu1, mu2, sigma)
T_prev = P(z[0], z[1])
T_next = P(z_new[0], z_new[1])
r = T_next / T_prev
if r > 1 or r > np.random.uniform(0, 1):
z = copy.copy(z_new)
sample.append(z)
accept.append(0)
else:
accept.append(1)
rate = np.mean(accept)
print(f'acceptance rate : {rate}')
return np.array(sample)
mu1 = 0
mu2 = 0
sigma = 1
N = 3000
samples = metropolis(N, mu1, mu2, sigma)
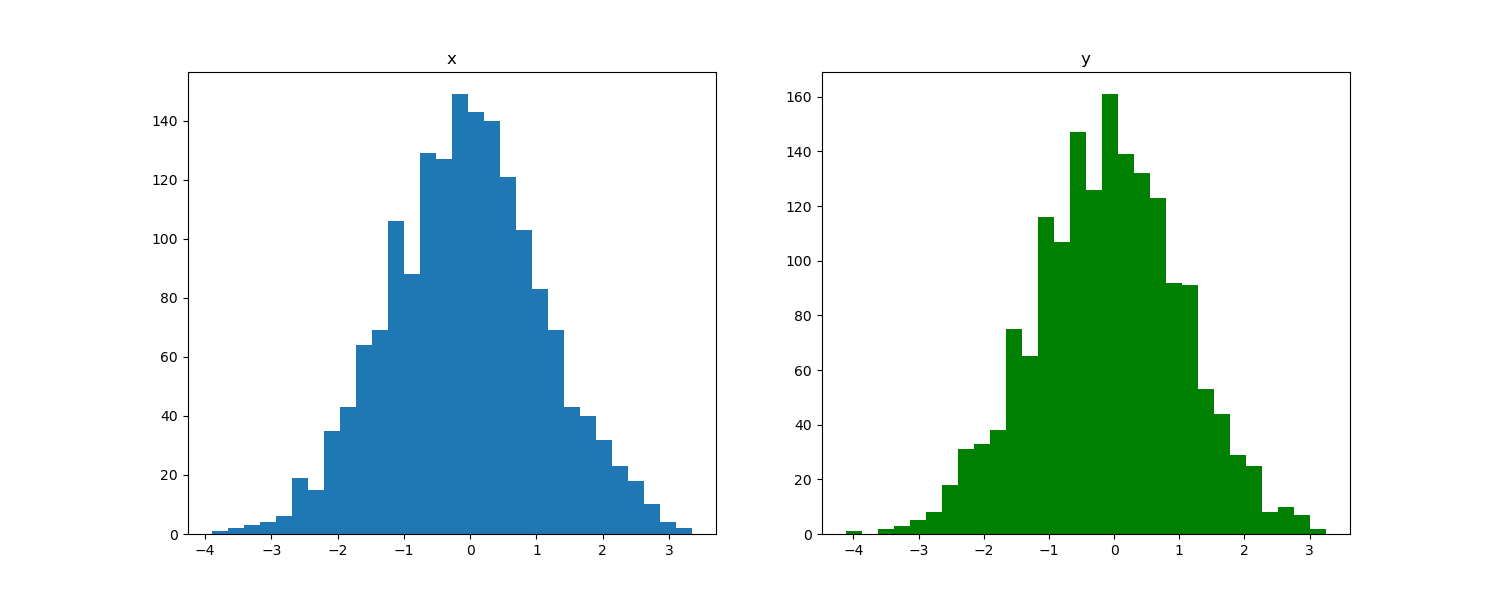
サンプルしたそれぞれの変数の分布は次の図のようになっていました。ガウス分布からMCMC法を用いてサンプリングしてくることに成功しているとみて良いでしょう。
M-H法の受容率(acceptance rate)は0.428でした。
M-H法において、サンプリングしたい事後分布$p(\mathbf{z})$は、問題設定により既に分かっています。提案分布により得られた$q(\mathbf{z}'|\mathbf{z})$は、詳細釣り合い条件を満たすような遷移確率であるとは限りませんので、
q(\mathbf{z}'|\mathbf{z})p(\mathbf{z}) > q(\mathbf{z}|\mathbf{z}')p(\mathbf{z}')
のように等号が成立しているとは限りません。
逆説的に、詳細釣り合い条件を満たすように遷移確率を設定できれば、事後分布$p(\mathbf{z})$からサンプリングできるので、
q(\mathbf{z}'|\mathbf{z})p(\mathbf{z})r = q(\mathbf{z}|\mathbf{z}')p(\mathbf{z}')
のようにある確率$r$で補正を行います。つまり、$\mathbf{z}$から$\mathbf{z}'$へ遷移したとき、それを確率rで採択すれば詳細釣り合い条件が満たされ、$p(\mathbf{z})$からサンプリングができます。
r = \frac{q(\mathbf{z}|\mathbf{z}')p(\mathbf{z}')}{q(\mathbf{z}'|\mathbf{z})p(\mathbf{z})}
$\mathbf{z}$から$\mathbf{z}'$へ遷移したとき、$r>1$となることもありますが、確率が大きく補正されることを意味するので無条件で採択することができます。
MCMC法にはM-H法の他にも代表的なものとしてHMC法やギブスサンプリングがあります。これらのアルゴリズムについてまとめ、比較した記事も執筆したのでもさらに詳しい解説が欲しい方は参照していただけると嬉しいです。
ハイパーパラメータ最適化
今回の記事で用いているカーネルは、 $\boldsymbol{\theta}=(\theta_1,\theta_2,\theta_3)$ の3つのハイパーパラメータが存在します。カーネルの計算結果は $\boldsymbol{\theta}$ の値に依存するので、それを明示すると次式のように書くことができます。
k(\mathbf{x_n},\mathbf{x_{n'}}\mid \boldsymbol{\theta})={\theta_1}\exp{(-\frac{|\mathbf{x}-\mathbf{x}'|^2}{\theta_2})} + \theta_3\delta(n, n')
学習データ $\mathbf{X}=(\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_n)$ および $\mathbf{y}=(y_1, y_2, \dots, y_n)$ とカーネルのハイパーパラメータ $\boldsymbol{\theta}$ が与えられたときの $\mathbf{y}$ の分布は次式のように求めることができます。
\begin{align}
P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})&=\mathbb{N}(\mathbf{y}|\mathbf{0},\mathbf{K}_{\boldsymbol \theta})\\
&=\frac{1}{(\sqrt{2\pi})^n}\frac{1}{\sqrt{|\mathbf{K}_{\boldsymbol \theta}|}}\exp{(-\frac{1}{2}\mathbf{y}^T\mathbf{K}_{\boldsymbol \theta}\mathbf{y})}
\end{align}
最尤法により最適な $\boldsymbol{\theta}$ は $P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})$ を最大化する $\boldsymbol{\theta}$ であると分かります。最尤法では尤度に対してlogを取ったlog尤度がよく用いられます。logは単調増加関数なので $\log{P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})}$ を最大化する $\boldsymbol{\theta}$ と $P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})$ を最大化する $\boldsymbol{\theta}$ は等価であります。
\begin{align}
\log{P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})}&=-\frac{n}{2}\log{(2\pi)}-\frac{1}{2}\log{|\mathbf{K}_{\boldsymbol \theta}|}-\frac{1}{2}\mathbf{y}^T\mathbf{K}_{\boldsymbol \theta}\mathbf{y}\\
&\propto -\frac{1}{2}\log{|\mathbf{K}_{\boldsymbol \theta}|}-\frac{1}{2}\mathbf{y}^T\mathbf{K}_{\boldsymbol \theta}\mathbf{y}
\end{align}
この式を用いてlog尤度を計算するプログラムは次の通りです。
def log_marginal_likelihood(theta_1, theta_2, theta_3):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(x_train[x_idx], x_train[x_prime_idx],
theta_1, theta_2, theta_3, x_idx == x_prime_idx)
y = y_train
yy = np.dot(np.linalg.inv(K), y_train)
return - (np.linalg.slogdet(K)[1] + np.dot(y, yy))
numpyのslogdet()関数は行列の行列式の対数を計算します。行列の行列式が非常に小さいか非常に大きい場合、行列式の計算がオーバーフローやアンダーフローすることがあります。求めたいのは行列の行列式の対数なので、slogdet()を用いることで行列式を直接計算するのを避けています。
log尤度を最大にする $\boldsymbol{\theta}$ をMCMC法を用いて求めるプログラムを実装していきます。
def optimize(x_train, y_train, bounds, initial_params=np.ones(3), n_iter=1000):
params = initial_params
bounds = np.atleast_2d(bounds)
# log transformation
log_params = np.log(params)
log_bounds = np.log(bounds)
log_scale = log_bounds[:, 1] - log_bounds[:, 0]
def log_marginal_likelihood(params):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(x_train[x_idx], x_train[x_prime_idx],
params[0], params[1], params[2], x_idx == x_prime_idx)
y = y_train
yy = np.dot(np.linalg.inv(K), y_train)
return - (np.linalg.slogdet(K)[1] + np.dot(y, yy))
lml_prev = log_marginal_likelihood(params)
thetas_list = []
lml_list = []
for _ in range(n_iter):
move = 1e-2 * np.random.normal(0, log_scale, size=len(params))
need_resample = (log_params +
move < log_bounds[:, 0]) | (log_params +
move > log_bounds[:, 1])
while(np.any(need_resample)):
move[need_resample] = np.random.normal(0, log_scale, size=len(params))[need_resample]
need_resample = (log_params +
move < log_bounds[:, 0]) | (log_params +
move > log_bounds[:, 1])
# proposed distribution
next_log_params = log_params + move
next_params = np.exp(next_log_params)
lml_next = log_marginal_likelihood(next_params)
r = np.exp(lml_next - lml_prev)
# metropolis update
if r > 1 or r > np.random.random():
params = next_params
log_params = next_log_params
lml_prev = lml_next
thetas_list.append(params)
lml_list.append(lml_prev)
return thetas_list[np.argmax(lml_list)]
この関数では初めにパラメータを対数スケールに変換しています。パラメータが全く未知な場合は、logスケールで探索する方が幅広く探索ができて効率が良いためです。
# log transformation
log_params = np.log(params)
log_bounds = np.log(bounds)
log_scale = log_bounds[:, 1] - log_bounds[:, 0]
関数の引数にあるboundsはパラメータの上限と下限を指定しています。平均0で分散log_scaleの正規分布からサンプルされたmoveを既にあるパラメータに加え、少しだけ「移動」させて提案分布を作ります。提案分布が指定されたboundsからはみ出ていた場合はサンプリングをし直します。
move = 1e-2 * np.random.normal(0, log_scale, size=len(params))
need_resample = (log_params + move < log_bounds[:, 0]) | (log_params + move > log_bounds[:, 1])
while(np.any(need_resample)):
move[need_resample] = np.random.normal(0, log_scale, size=len(params))[need_resample]
need_resample = (log_params + move < log_bounds[:, 0]) | (log_params + move > log_bounds[:, 1])
この部分でメトロポリス判定を行なっています。
# metropolis update
if r > 1 or r > np.random.random():
params = next_params
log_params = next_log_params
lml_prev = lml_next
thetas_list.append(params)
lml_list.append(lml_prev)
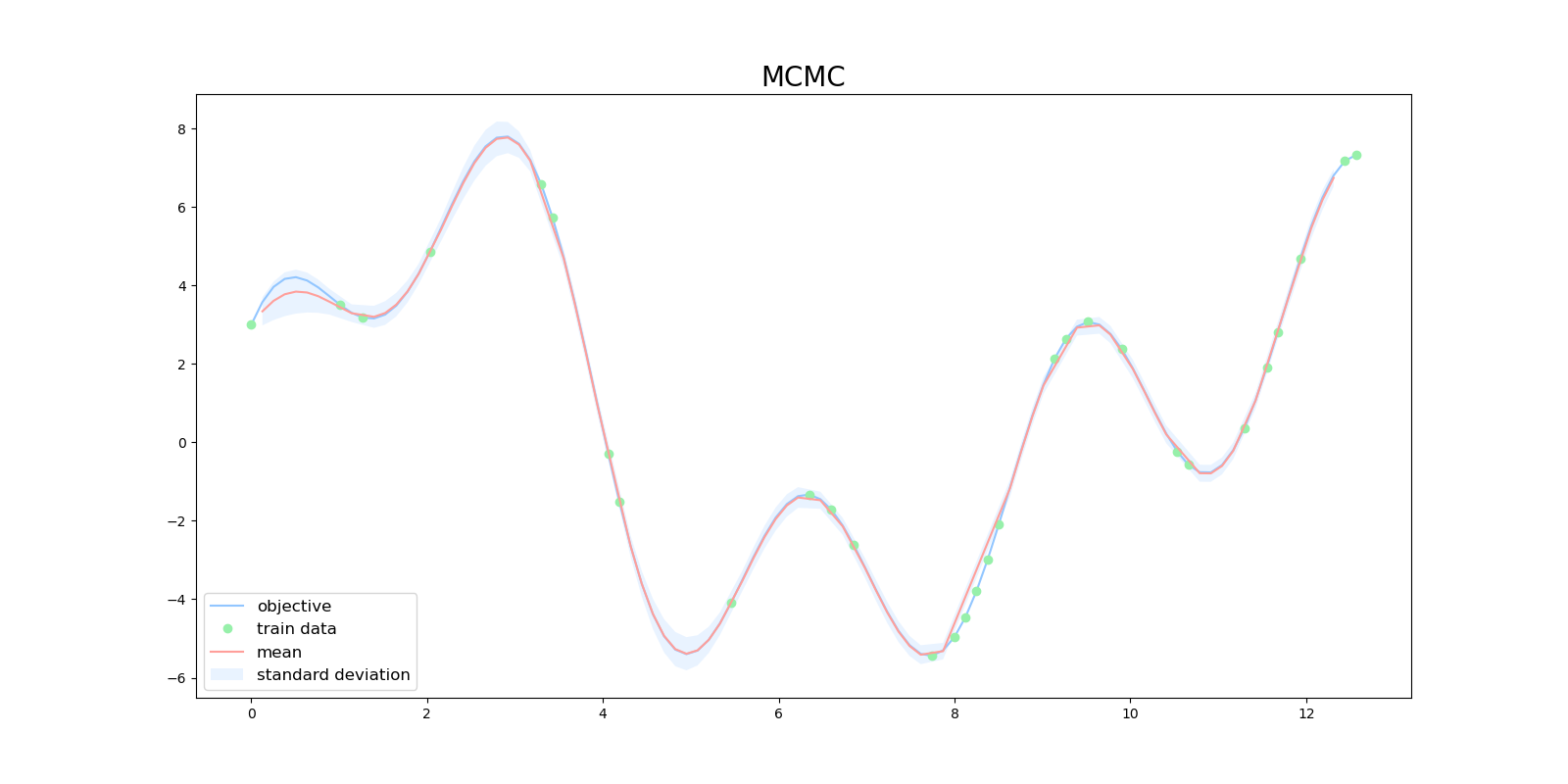
MCMCでハイパーパラメータを最適化した上でガウス過程を実行すると次のような結果がえられました。
def gpr(x_train, y_train, x_test):
# average
mu = []
# variance
var = []
train_length = len(x_train)
test_length = len(x_test)
thetas = optimize(x_train, y_train, bounds=np.array(
[[1e-2, 1e2], [1e-2, 1e2], [1e-2, 1e2]]), initial_params=np.array([0.5, 0.5, 0.5]))
print(thetas)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], thetas[0], thetas[1], thetas[2], x_idx == x_prime_idx)
yy = np.dot(np.linalg.inv(K), y_train)
for x_test_idx in range(test_length):
k = np.zeros((train_length,))
for x_idx in range(train_length):
k[x_idx] = kernel(
x_train[x_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_idx == x_prime_idx)
s = kernel(
x_test[x_test_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_idx == x_prime_idx)
mu.append(np.dot(k, yy))
kK_ = np.dot(k, np.linalg.inv(K))
var.append(s - np.dot(kK_, k.T))
return np.array(mu), np.array(var)
同じ初期値 $\boldsymbol{\theta}=(0.5, 0.5, 0.5)$ から始めましたが、ハイパーパラメータを最適化しないで実行したときと比べて、うまく回帰できるようになっていました。このときハイパーパラメータの最適値は $\boldsymbol{\theta}=(26.294,2.828,0.01)$ でした。
勾配法による最適化
ご存知の方も多いと思いますが、勾配法とは現在の点 $x_i$ の勾配を用いて、値を次式のように更新し続けることで関数の最大値や最小値を求める手法のことを指します。
x_{i+1}=x_i - \alpha\frac{df}{dx_i}
$\mathbf{y}$ の条件付き分布 $P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})$ は $\boldsymbol{\theta}$ の関数なので、 $\boldsymbol{\theta}$ で微分することができます。行列の微分に関する公式の証明は省略します。
\begin{align}
\log{P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})}&=-\frac{n}{2}\log{(2\pi)}-\frac{1}{2}\log{|\mathbf{K}_{\boldsymbol \theta}|}-\frac{1}{2}\mathbf{y}^T\mathbf{K}_{\boldsymbol \theta}\mathbf{y}\\
&\propto -\frac{1}{2}\log{|\mathbf{K}_{\boldsymbol \theta}|}-\frac{1}{2}\mathbf{y}^T\mathbf{K}_{\boldsymbol \theta}\mathbf{y}
\end{align}
\frac{\partial}{\partial\boldsymbol{\theta}}\log{|\mathbf{K}_{\boldsymbol{\theta}}|}=\textrm{tr}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}})
\frac{\partial}{\partial\boldsymbol{\theta}}\mathbf{K}_{\boldsymbol{\theta}}^{-1}=-\mathbf{K}_{\boldsymbol{\theta}}^{-1}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}}\mathbf{K}_{\boldsymbol{\theta}}^{-1}
\frac{\partial}{\partial\boldsymbol{\theta}}\log{P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})}=-\frac{1}{2}\textrm{tr}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}})+\frac{1}{2}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\mathbf{y})^T\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\mathbf{y})
今回の記事では次に示す $\boldsymbol{\theta}=(\theta_1,\theta_2,\theta_3)$ をパラメータにもつカーネルを用いています。
k(\mathbf{x_n},\mathbf{x_{n'}}\mid \boldsymbol{\theta})={\theta_1}\exp{(-\frac{|\mathbf{x}-\mathbf{x}'|^2}{\theta_2})} + \theta_3\delta(n, n')
log尤度の勾配を計算するには、カーネルを $\boldsymbol{\theta}$ で微分したときの値が必要になります。カーネル $k(\mathbf{x_n},\mathbf{x_{n'}})$ を $\theta_1,\theta_2,\theta_3$ それぞれで微分した値を求めると次式のようになります。
\frac{\partial k}{\partial \theta_1}={\theta_1}\exp{(-\frac{|\mathbf{x}-\mathbf{x}'|^2}{\theta_2})}=k(\mathbf{x_n},\mathbf{x_{n'}})-\theta_3\delta(n, n')
\begin{align}
\frac{\partial k}{\partial \theta_2}&={\theta_1}\exp{(-\frac{|\mathbf{x}-\mathbf{x}'|^2}{\theta_2})}\frac{\partial}{\partial \theta_2}(-\frac{|\mathbf{x}-\mathbf{x}'|^2}{\theta_2})\\
&=(k(\mathbf{x_n},\mathbf{x_{n'}})-\theta_3\delta(n, n'))\frac{|\mathbf{x}-\mathbf{x}'|^2}{\theta_2}
\end{align}
\frac{\partial k}{\partial \theta_3}=\theta_3\delta(n, n')
今まで使っていたカーネルを、ある点 $x$ における勾配を返すこともできるように拡張します。eval_gradがTrueのときは、カーネルの値とともに勾配の値も戻り値としています。
# Radiant Basis Kernel + Error
def kernel(x, x_prime, theta_1, theta_2, theta_3, noise, eval_grad=False):
# delta function
if noise:
delta = theta_3
else:
delta = 0
if eval_grad:
dk_dTheta_1 = kernel(x, x_prime, theta_1, theta_2, theta_3, noise) - delta
dk_dTheta_2 = (kernel(x, x_prime, theta_1, theta_2, theta_3, noise) - delta) * ((x - x_prime)**2) / theta_2
dk_dTheta_3 = delta
return rbf(x, x_prime, theta_1=theta_1, theta_2=theta_2) + \
delta, np.array([dk_dTheta_1, dk_dTheta_2, dk_dTheta_3])
return rbf(x, x_prime, theta_1=theta_1, theta_2=theta_2) + delta
導出した勾配の式を使って、log尤度の勾配を計算するプログラムを実装します。
プログラムではnp.einsum()という関数が使われています。np.einsum()はアインシュタインの縮約記法と呼ばれる記法で計算をする方法です。詳しく知りたい人はこちらの記事が参考になると思います。
def log_likelihood_gradient(params):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
dK_dTheta = np.zeros((3, train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
k, grad = kernel(x_train[x_idx], x_train[x_prime_idx], params[0],
params[1], params[2], x_idx == x_prime_idx, eval_grad=True)
K[x_idx, x_prime_idx] = k
dK_dTheta[0, x_idx, x_prime_idx] = grad[0]
dK_dTheta[1, x_idx, x_prime_idx] = grad[1]
dK_dTheta[2, x_idx, x_prime_idx] = grad[2]
K_inv = np.linalg.inv(K)
yy = np.dot(K_inv, y_train)
tr = np.einsum("ijj", np.einsum("ij,kjl->kil", K_inv, dK_dTheta))
return - tr + np.einsum("i,ji->j", yy.T, np.einsum("ijk,k->ij", dK_dTheta, yy))
最後に勾配法を用いてハイパーパラメータを最適化するプログラムを実装します。さまざまな勾配法のアルゴリズムが存在しますが、今回の実装ではL-BFGS法を用いました。scikit-learnのデフォルトのガウス過程で用いられている最適化アルゴリズムもL-BFGS法になります。用いるアルゴリズムは勾配法であればなんでも良いです。
def optimize(x_train, y_train, bounds, initial_params=np.ones(3)):
bounds = np.atleast_2d(bounds)
def log_marginal_likelihood(params):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], params[0], params[1], params[2], x_idx == x_prime_idx)
yy = np.dot(np.linalg.inv(K), y_train)
return - (np.linalg.slogdet(K)[1] + np.dot(y_train, yy))
def log_likelihood_gradient(params):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
dK_dTheta = np.zeros((3, train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
k, grad = kernel(x_train[x_idx], x_train[x_prime_idx], params[0],
params[1], params[2], x_idx == x_prime_idx, eval_grad=True)
K[x_idx, x_prime_idx] = k
dK_dTheta[0, x_idx, x_prime_idx] = grad[0]
dK_dTheta[1, x_idx, x_prime_idx] = grad[1]
dK_dTheta[2, x_idx, x_prime_idx] = grad[2]
K_inv = np.linalg.inv(K)
yy = np.dot(K_inv, y_train)
tr = np.einsum("ijj", np.einsum("ij,kjl->kil", K_inv, dK_dTheta))
return - tr + np.einsum("i,ji->j", yy.T, np.einsum("ijk,k->ij", dK_dTheta, yy))
def obj_func(params):
lml = log_marginal_likelihood(params)
grad = log_likelihood_gradient(params)
return -lml, -grad
opt_res = scipy.optimize.minimize(
obj_func,
initial_params,
method="L-BFGS-B",
jac=True,
bounds=bounds,
)
theta_opt, func_min = opt_res.x, opt_res.fun
return theta_opt, func_min
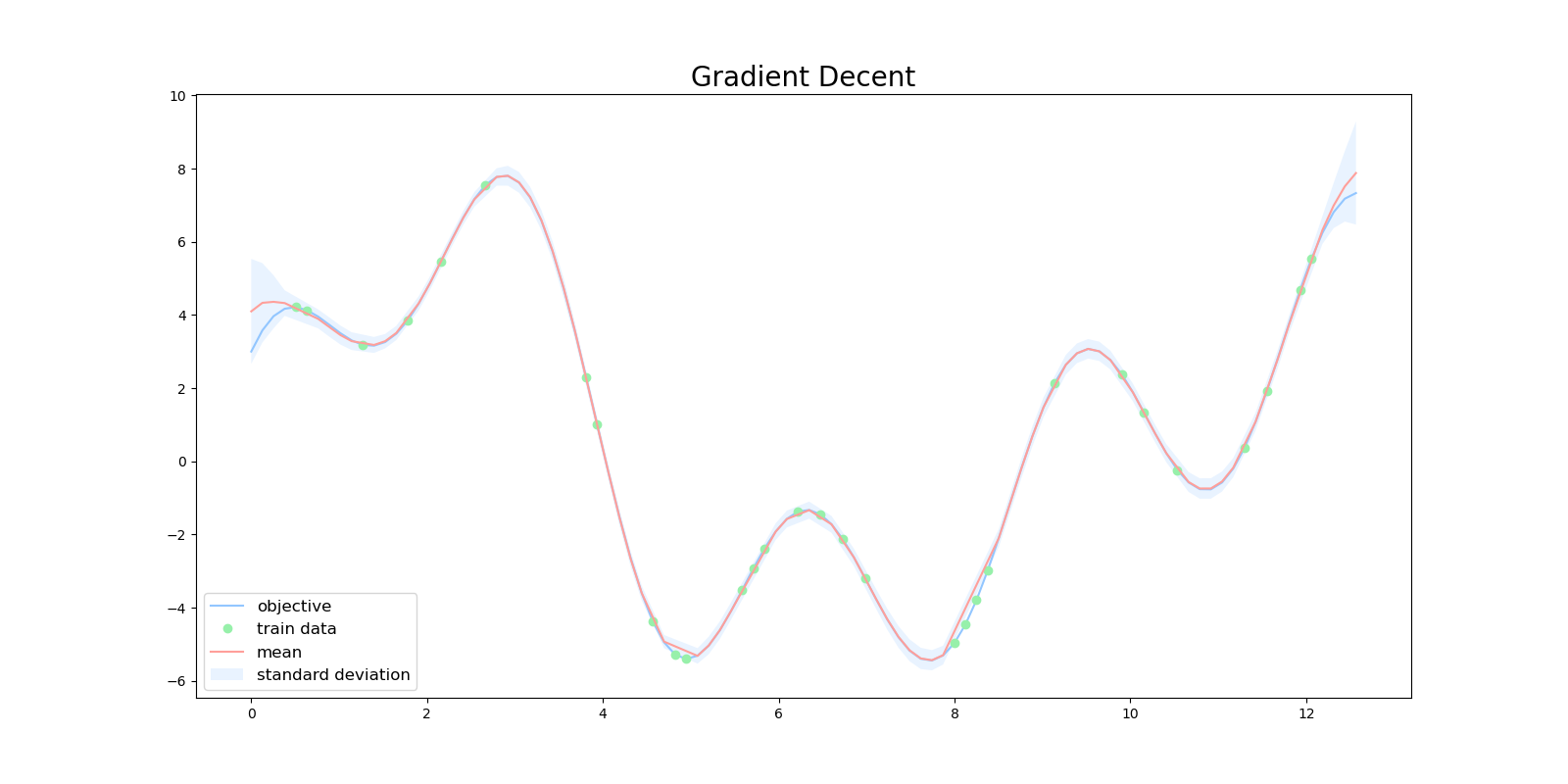
勾配法を用いてハイパーパラメータを最適化した上でガウス過程を実行すると次のような結果が得られました。
def gpr(x_train, y_train, x_test):
# average
mu = []
# variance
var = []
train_length = len(x_train)
test_length = len(x_test)
thetas, _ = optimize(x_train, y_train, bounds=np.array(
[[1e-2, 1e2], [1e-2, 1e2], [1e-2, 1e2]]), initial_params=np.array([0.5, 0.5, 0.5]))
print(thetas)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], thetas[0], thetas[1], thetas[2], x_idx == x_prime_idx)
yy = np.dot(np.linalg.inv(K), y_train)
for x_test_idx in range(test_length):
k = np.zeros((train_length,))
for x_idx in range(train_length):
k[x_idx] = kernel(
x_train[x_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_idx == x_test_idx)
s = kernel(
x_test[x_test_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_test_idx == x_test_idx)
mu.append(np.dot(k, yy))
kK_ = np.dot(k, np.linalg.inv(K))
var.append(s - np.dot(kK_, k.T))
return np.array(mu), np.array(var)
こちらもMCMC法を用いたときと同様に、同じ初期値 $\boldsymbol{\theta}=(0.5, 0.5, 0.5)$ から始めましたが、ハイパーパラメータを最適化しないで実行したときと比べて、うまく回帰できるようになっていました。このときハイパーパラメータの最適値は $\boldsymbol{\theta}=(37.985,3.264,0.01)$ でした。
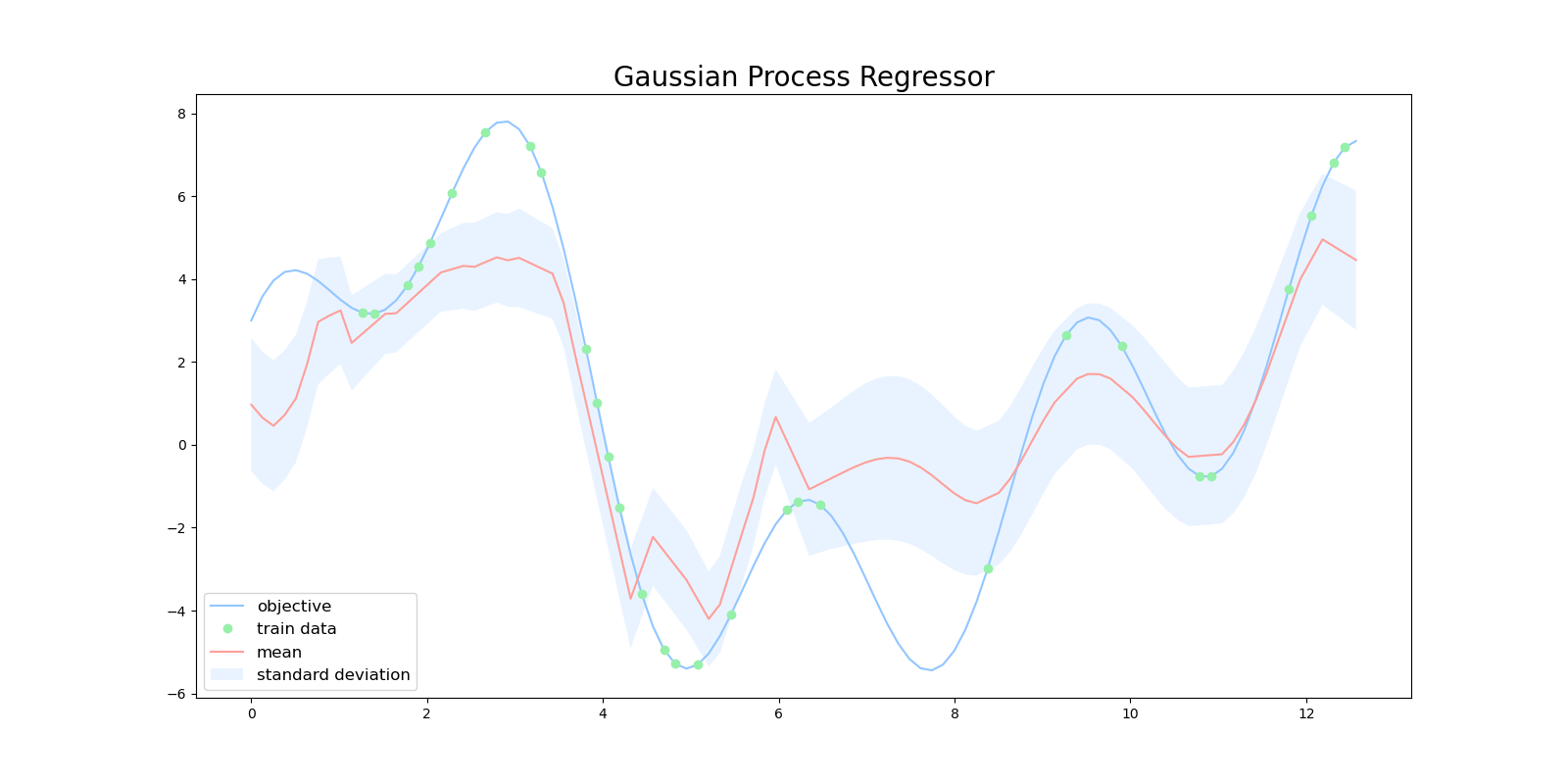
今までと同様に初期値 $\boldsymbol{\theta}=(0.5, 0.5, 0.5)$ から勾配法を用いて、ガウス過程を何度が実行していると次のような出力が得られることがあります。勾配法では最適化の最中に局所解にトラップされて、うまく最適なパラメータに辿り着けない場合があります。その結果、下図のようなうまく回帰ができない出力になる場合もあります。
まとめ
ガウス過程のハイパーパラメータを最適化するプログラムをゼロから実装してみました。
ハイパーパラメータが調整されたことで、「ある程度」使えそうなアルゴリズムになったのではないかと思います。しかしながら、ガウス過程では行列の逆行列を計算する際に $O(N^3)$ の計算量を必要とします。この計算量では、データの量が増えるとすぐに対応できなくなってしまいます。
次回の記事では、今までに作ったガウス過程のプログラムに対して、計算量を削減するアルゴリズムを追加してみようと思います。
ここまで読んでいただきありがとうございます。
今回実装したコードは全てこちらのレポジトリにあります。
参考文献
[1] C. E. Rasmussen and C. K. I. Williams. Gaussian Processes for Machine Learning. 2006.
[2] Jaehoon Lee, Yasaman Bahri. Deep Neural Networks as Gaussian Processes. 2018.
[3] Robert B. Gramacy. Gaussian Process Modeling, Design and Optimization for the Applied Science. 2021.
[4] 持橋 大地, ガウス過程と機械学習. 2019.