ガウス過程 from Scratch

ガウス過程(Gaussian Process) はノンパラメトリックなモデルの一つで、一般的に「関数を出力する箱」というような例えられ方をします。このようにたとえられる理由は、ガウス過程では関数 $f(x)$ を確率変数と見立てて、 $f(x)$ の確率分布を出力するためです。

ガウス過程は、ベイズ最適化や空間統計学の文脈でよく用いられます。また、最近になって深層学習が発展するにつれて、ニューラルネットワークとガウス過程の等価性が示され(Lee et al, 2018)、注目を集めるようにもなりました。具体的には、隠れ層が１層のニューラルネットワークで隠れ層のユニット数を $\infty$ にすると、中心極限定理によりニューラルネットワークの出力はガウス過程と等価になります。

この記事では、ガウス過程をゼロから実装してみることで、ガウス過程への理解を深めることを目的にしています。

理論的な部分に関しては、簡単にまとめますが、この記事では深くは立ち入らないようにします。理論的な理解も深めたい方は、下記の記事などを参照するのが良いかと思われます。

参考文献

[1] C. E. Rasmussen and C. K. I. Williams. Gaussian Processes for Machine Learning. 2006.
[2] Jaehoon Lee, Yasaman Bahri. Deep Neural Networks as Gaussian Processes. 2018.
[3] Robert B. Gramacy. Gaussian Process Modeling, Design and Optimization for the Applied Science. 2021.
[5] 持橋 大地, ガウス過程と機械学習. 2019.

※注意
この記事は筆者が勉強したことをまとめて、理解を深めるために執筆しています。内容に誤り等があった場合は、コメント等でご指摘いただけると幸いです。

イントロダクション

ガウス過程はノンパラメトリックなモデルの一つです。パラメトリックなモデルは、データがある部分にはよくフィットする一方で、将来的な予測精度はパラメータに依存します。ノンパラメトリックなモデルは、少ないデータでも妥当な予測が可能ですが、データがある部分の精度はパラメトリックなモデルに劣ることが多いです。

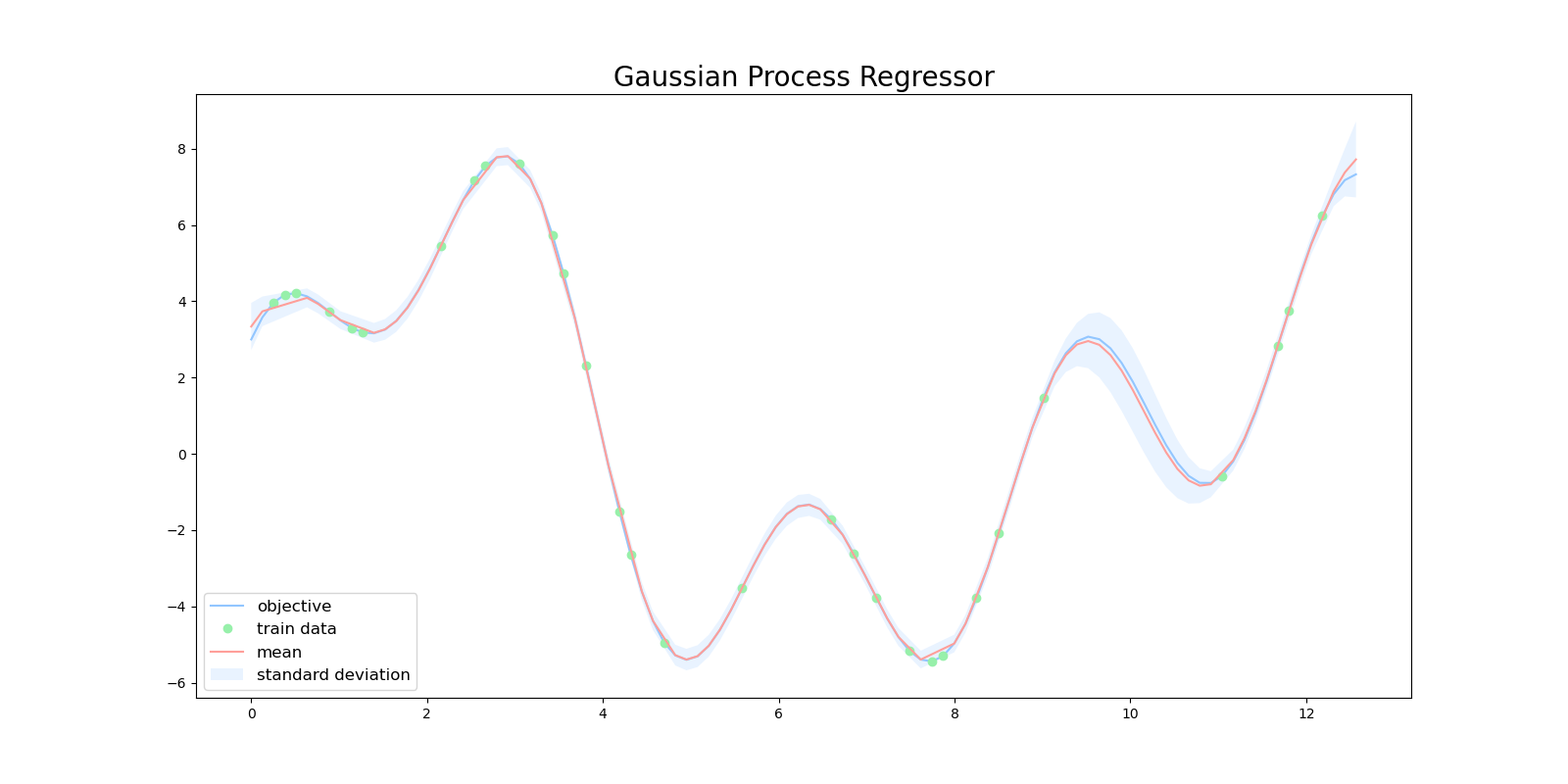
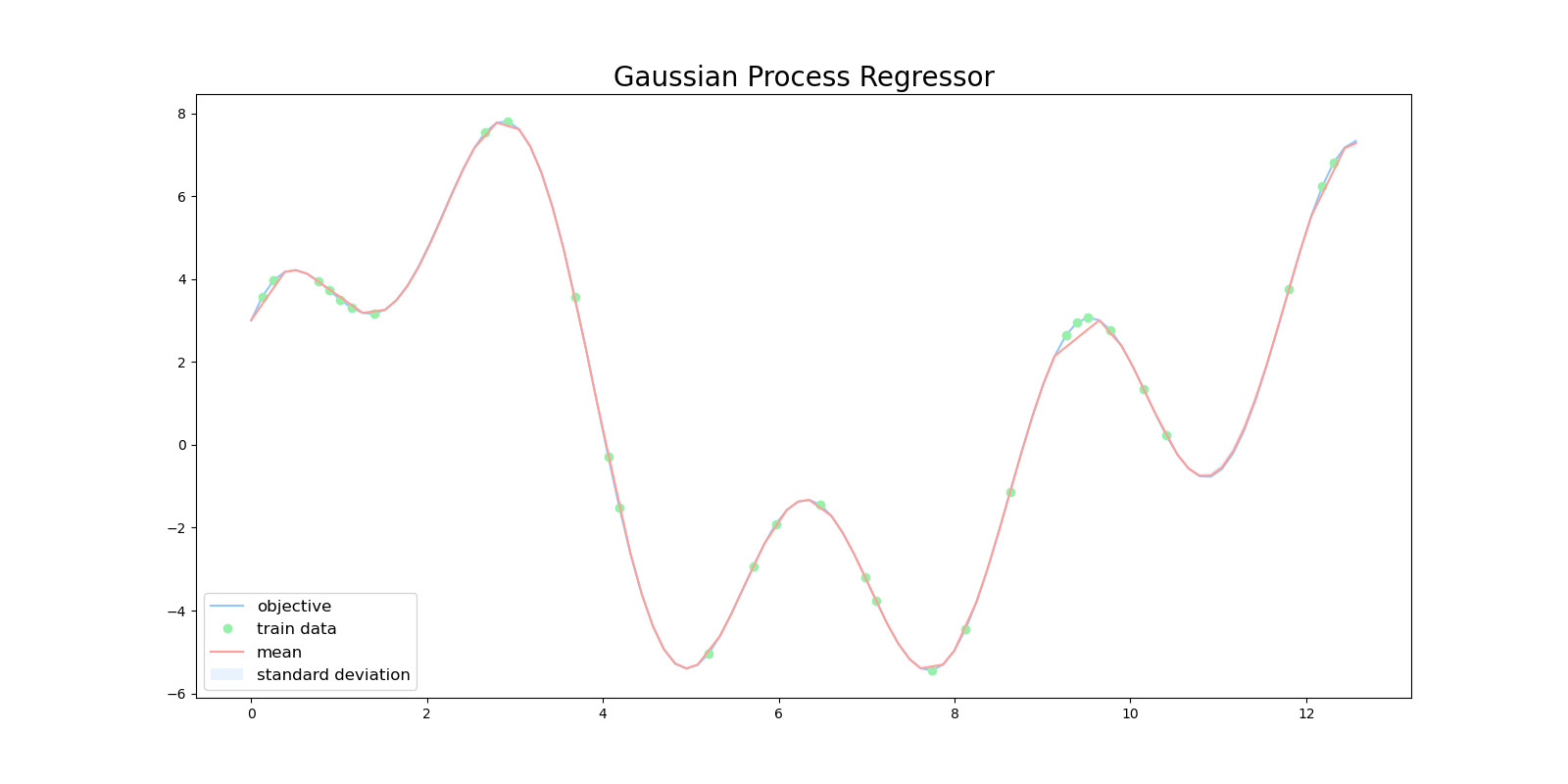
特にガウス過程は、ガウス分布の平均と分散を出力するので、ある予測に対する信頼度を表現することができます。下図は、ガウス過程を用いて目的関数を回帰した図になります。緑色の点が学習用データで、赤い線が平均値、水色の領域は全体の95%の信頼区間を表しています。

$x=10$ 周辺に注目すると、この区間では訓練データが少ないため、ガウス過程の出力も自信がない(分散が大きい)ものになっています。

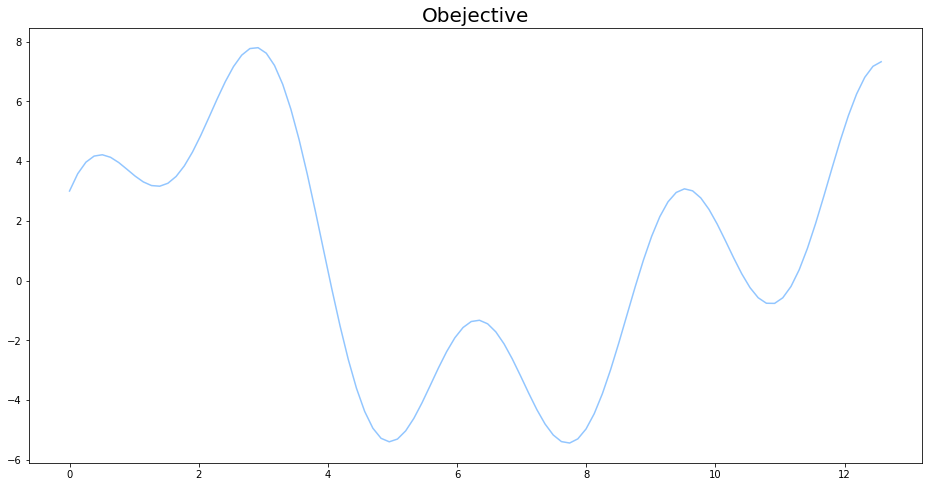
目的関数

今回の記事で回帰を行う目的関数は、

f(x)=2\sin{(x)}+3\cos{(x)}+5\sin{(\frac{2}{3}x)} \\
0 \leq x \leq 4\pi

とします。pythonによる実装は以下の通りです。

def objective(x):
    return 2 * np.sin(x) + 3 * np.cos(2 * x) + 5 * np.sin(2 / 3 * x)

ガウス過程(Gaussian Process)

ガウス分布の形をした基底関数をグリッド状に配置して、適当に重み $w_i$ で重みづけると、任意の形の関数が表すことができます。これを 動径基底関数回帰(Radial Basis Function Regression) と呼びます。

\phi_h(x)=\exp(-\frac{(x-u_h)^2}{\sigma^2})

y=\sum_{h=-H}^{H}w_h\phi{(x)}

[出典]「ガウス過程と機械学習」サポートページ

しかしながら、動径基底関数回帰には問題点があります。例えば、グラフ上の-10~10の間にメモリ1毎に動径基底関数を配置していくと、 $\mathbf{x}$ が2次元なら441の動径基底関数が必要になり、 $\mathbf{x}$ が2次元なら441個の動径基底関数が必要になり、 $\mathbf{x}$ が5次元なら4084101個の動径基底関数が必要になります。

動径基底関数回帰では、次元の呪いによって $\mathbf{x}$ の次元が大きくなるとすぐに、現実的な計算可能リソースを超えてしまうのです。

次元の呪いを解消する手段として、$\mathbf{w}$について期待値をとって、モデルから積分消去するというアイデアがあります。

\begin{pmatrix}\hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_N \end{pmatrix}=
\begin{pmatrix} 
  \phi_0(\mathbf{x_1}) & \phi_1(\mathbf{x_1}) & \dots  & \phi_H(\mathbf{x_1}) \\
  \phi_0(\mathbf{x_2}) & \phi_1(\mathbf{x_2}) & \dots  & \phi_H(\mathbf{x_2}) \\
  \vdots & \vdots & \ddots & \vdots \\
  \phi_0(\mathbf{x_N}) & \phi_1(\mathbf{x_N}) & \dots  & \phi_H(\mathbf{x_N})
\end{pmatrix}
\begin{pmatrix}w_0 \\ w_1 \\ \vdots \\ w_H \end{pmatrix}

\mathbf{\hat{y}}=\mathbf{\Phi}\mathbf{w}

重み $\mathbf{w}$ が平均 $\mathbf{0}$ で分散 $\lambda^2\mathbf{I}$ のガウス分布

\mathbf{w}\sim{N(\mathbf{0},\lambda^2\mathbf{I})}

から生成されたものとします。

ガウス分布の性質より、ガウス分布に従うベクトルを線形変換したものもガウス分布に従う(証明は省略)ので、 $\mathbf{y}$ は平均 $\mathbf{0}$ で分散 $\lambda^2\mathbf{\Phi}\mathbf{\Phi}^T$ のガウス分布に従います。

E[\mathbf{y}]=E[\mathbf{\Phi}\mathbf{w}]=\mathbf{\Phi}E[\mathbf{w}]=\mathbf{0}

\begin{align}
\mathbf{\Sigma}&=E[\mathbf{y}\mathbf{y}^T]-E[\mathbf{y}]E[\mathbf{y}]^T=E[(\mathbf{\Phi}\mathbf{w})(\mathbf{\Phi}\mathbf{w})^T]\\
&=\mathbf{\Phi}E[\mathbf{w}\mathbf{w}^T]\mathbf{\Phi}^T=\lambda^2\mathbf{\Phi}\mathbf{\Phi}^T
\end{align}

\mathbf{y}\sim \mathbb{N}(\mathbf{0},\lambda^2\mathbf{\Phi}\mathbf{\Phi}^T)

このとき、 $\mathbf{y}$ の分布は $K_{n{n'}}=\lambda^2{\phi(\mathbf{x_n})\phi(\mathbf{x_{n'}})^T}$ によって決まります。 $k(\mathbf{x_n},\mathbf{x_{n'}})={\phi(\mathbf{x_n})^T\phi(\mathbf{x_{n'}})^T}$ を カーネル関数(kernel) と呼び、データに応じて適切なカーネル関数選択することでガウス過程の性能が向上します。

$\mathbf{y}\sim \mathbb{N}(\mathbf{0},\lambda^2\mathbf{\Phi}\mathbf{\Phi}^T)$ によると、重み $\mathbf{w}$ は期待値を取ったので消えています。ガウス過程では、重み　$\mathbf{w}$　について期待値を取ることで次元の呪いを回避しています。

どんなN個の入力の集合 $(\mathbf{x_{1}},\mathbf{x_{2}},\dots,\mathbf{x_{N}})$ についても、対応する出力 $(f(\mathbf{x_{1}}),f(\mathbf{x_{2}}),\dots,f(\mathbf{x_{N}}))$ の同時分布 $p(\mathbf{f})$ が、平均 $\mathbf{u}$ と $K_{n{n'}}=k(\mathbf{x_n},\mathbf{x_{n'}})$ を要素とする共分散行列 $\mathbf{K}$ のガウス分布 $\mathbb{N}(\mathbf{u},\mathbf{K})$ に従うとき、 $\mathbf{f}$ は ガウス過程(Gaussian Process) に従うと言います。

\mathbf{f}\sim \textrm{GP}(\mathbf{u},k(\mathbf{x},\mathbf{x'}))

ガウス過程は，ある$\mathbf{x}$に対してスカラー$f(\mathbf{x})$を返すのではなく，$\mathbf{x}$における$f(\mathbf{x})$が従う正規分布の平均と分散を出力します。

一般的に観測する $y$ にはノイズがのっていることが多いので、

y = f(\mathbf{x})+\epsilon

\epsilon\sim \mathbb{N}(0,\sigma^2)

とするのが自然です。このとき、関数 $\mathbf{f}$ が与えられたときの　$\mathbf{y}$ の分布 $p(\mathbf{y}\mid\mathbf{f})$ は

p(\mathbf{y}\mid\mathbf{f})=\mathbb{N}(\mathbf{f}, \sigma^2 \mathbf{I})

と表すことができます。入力 $\mathbf{X}$ が与えられたときの $\mathbf{y}$ の分布は $p(\mathbf{y}\mid \mathbf{X})$ は

\begin{align}
p(\mathbf{y}\mid\mathbf{X}) &= \int p(\mathbf{y}, \mathbf{f} \mid \mathbf{X}) d\mathbf{f} \\
&= \int p(\mathbf{y}\mid\mathbf{f})p(\mathbf{f}\mid\mathbf{X}) d\mathbf{f} \\
&= \int \mathbb{N}(\mathbf{y}\mid\mathbf{f},\sigma^2\mathbf{I})\mathbb{N}(\mathbf{f}\mid\mathbf{u},\mathbf{K})d\mathbf{f} \\
\end{align}

となります。ガウス分布の再生性(証明は省略)より

p(\mathbf{y}\mid\mathbf{X})=\mathbb{N}(\mathbf{u},\mathbf{K}+\sigma^2\mathbf{I})

と表されます。よって、ノイズを考慮した上でのガウス過程は、 $K_{n{n'}}=k(\mathbf{x_n},\mathbf{x_{n'}})$ を要素とする共分散行列 $\mathbf{K}$ の対角成分に、 $\sigma^2$　を足したものとして表現できます。

k'(\mathbf{x_n},\mathbf{x_{n'}})=k(\mathbf{x_n},\mathbf{x_{n'}})+\sigma^2\delta(n,n')

カーネル(Kernel)

共分散行列 $\mathbf{K}$ はカーネル関数 $k(\mathbf{x_n},\mathbf{x_{n'}})$ の計算結果さえ分かれば計算ができるので、$\phi(\mathbf{x})$を明示的に求める必要はありません。これを カーネルトリック(Kernel Trick) と呼びます。

カーネル関数をプロットする関数を実装します。

def plot_kernel(kernel, title):
    n = 100
    x = np.linspace(-10, 10, n)
    ys = []
    
    for i in range(3):
        mkernel = np.zeros((x.shape[0], x.shape[0]))
        for i_row in range(x.shape[0]):
            for i_col in range(i_row, x.shape[0]):
                mkernel[i_row, i_col] = kernel(x[i_row], x[i_col])
                mkernel[i_col, i_row] = mkernel[i_row, i_col]
        
        K = 1**2 * np.dot(mkernel, mkernel.T)
        y = np.random.multivariate_normal(np.zeros(len(x)), K)
        ys.append(y)
    
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    for y in ys:
        ax.plot(x, y)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_title(f'{title}')

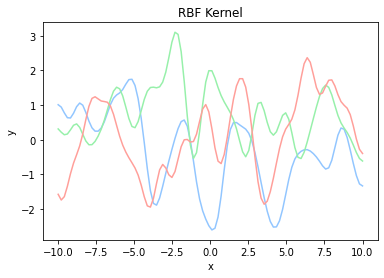
カーネルにはさまざまな種類があり、次に示す ガウスカーネル(Gaussian Kernel) などが一般的によく用いられます。$\theta_1$と$\theta_2$はハイパーパラメータであり、データに合わせて調整する必要があります。

k(\mathbf{x_n},\mathbf{x_{n'}})={\theta_1}\exp{(-\frac{|\mathbf{x}-\mathbf{x}'|}{\theta_2})}

ガウスカーネルの実装は数式をそのままプログラムに変換するだけで事足ります。

def rbf(x, x_prime, theta_1, theta_2):    
    return theta_1 * np.exp(-1 * (x - x_prime)**2 / theta_2)

plot_kernel(lambda x, x_prime: rbf(x, x_prime, 0.5, 0.5), 'RBF Kernel')

ガウスカーネルの他にも、 周期カーネル(Periodic Kernel) や 線形カーネル(Linear Kernel) 、 指数カーネル(Exponential Kernel) などがあります。

k(\mathbf{x_n},\mathbf{x_{n'}})=\exp{({\theta_1} \cos(\frac{|\mathbf{x}-\mathbf{x}'|}{\theta_2}))}

k(\mathbf{x_n},\mathbf{x_{n'}})= \mathbf{x_n}\mathbf{x_{n'}} + \theta

k(\mathbf{x_n},\mathbf{x_{n'}})= \exp{(-\frac{|\mathbf{x_n} - \mathbf{x_{n'}}|}{\theta})}

def periodic(x, x_prime, theta_1, theta_2):
    return np.exp(theta_1 * np.cos((x - x_prime) /theta_2))

def linear(x, x_prime, theta):
    return x * x_prime + theta

def exp(x, x_prime, theta):
    return np.exp(-np.abs(x - x_prime) / theta)

plot_kernel(lambda x, x_prime: periodic(x, x_prime, 0.5, 0,5), 'Periodic Kernel')
plot_kernel(lambda x, x_prime: exp(x, x_prime, 0.5), 'Linear Kernel')
plot_kernel(lambda x, x_prime: exp(x, x_prime, 0.5), 'Exponential Kernel')

周期カーネル	線形カーネル	指数カーネル

カーネルは複数を組み合わせて使うこともできます。株価などの周期性があり細かい変動が多いデータに対しては、指数カーネルで細かい変動を表し、周期カーネルで周期性を表すとを使うと、うまくフィッティングできそうな気がします。

kernel = lambda x, x_prime: 0.8 * exp(x, x_prime, 0.5) + 0.2 * periodic(x, x_prime, 0.5, 0.5)
plot_kernel(kernel, 'Exponential + Periodic Kernel')

ガウス過程による予測

データに含まれない $\mathbf{x*}$ による $y*$ の予測値は、 $\mathbf{y}$ に $y*$ を含めた全体がまたガウス分布に従うことから

\begin{pmatrix}\mathbf{y} \\ y^{*}  \end{pmatrix}{\sim}N(\mathbf{0},
\begin{pmatrix}
  \mathbf{K} & \mathbf{k_*}  \\
  \mathbf{k_*^T} & k_{**} 
\end{pmatrix}
)

とすることで、ガウス分布の性質を用いて計算することができます。

p(y^{*}{\mid}\mathbf{x^*}, D)=N(\mathbf{k_*^T}\mathbf{K}^{-1}\mathbf{y},k_{**}-\mathbf{k_*^T}\mathbf{K}^{-1}\mathbf{k})

D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),\dots,(\mathbf{x_N},y_N)\}

予測値が複数ある場合も同様にして計算ができます。

\begin{pmatrix}\mathbf{y} \\ y^{*}_1 \\ \vdots \\ y^{*}_M \end{pmatrix}{\sim}N(\mathbf{0},
\begin{pmatrix}
  \mathbf{K} & \mathbf{k_*}  \\
  \mathbf{k_*^T} & \mathbf{k_{**}} 
\end{pmatrix}

p(\mathbf{y^{*}}{\mid}\mathbf{x^*}, D)=N(\mathbf{k_*^T}\mathbf{K}^{-1}\mathbf{y},\mathbf{k_{**}}-\mathbf{k_*^T}\mathbf{K}^{-1}\mathbf{k})

ガウス過程回帰を実装していきます。
初めにデータを訓練用のデータとテスト用のデータに分割する関数を実装します。データ全体のうち、3割を訓練データ、残り7割をテストデータに分割します。

def train_test_split(x, y, test_size):
    assert len(x) == len(y)
    n_samples = len(x)
    test_indices = np.sort(
        np.random.choice(
            np.arange(n), int(
                n_samples * test_size), replace=False))
    train_indices = np.ones(n_samples, dtype=bool)
    train_indices[test_indices] = False
    test_indices = ~ train_indices

    return x[train_indices], x[test_indices], y[train_indices], y[test_indices]

n = 100
data_x = np.linspace(0, 4 * np.pi, n)
data_y = objective(data_x)


x_train, x_test, y_train, y_test = train_test_split(data_x, data_y, test_size=0.70)

次にガウス過程回帰の結果をプロットする関数を作成します。この関数は、目的関数、訓練データ点、ガウス過程回帰が返す平均と標準偏差をプロットします。

def plot_gpr(x_train, y_train, x_test, mu, var):
    plt.figure(figsize=(16, 8))
    plt.title('Gaussian Process Regressor', fontsize=20)

    plt.plot(data_x, data_y, label='objective')
    plt.plot(
        x_train,
        y_train,
        'o',
        label='train data')

    std = np.sqrt(np.abs(var))

    plt.plot(x_test, mu, label='mean')

    plt.fill_between(
        x_test,
        mu + 2 * std,
        mu - 2 * std,
        alpha=.2,
        label='standard deviation')
    plt.legend(
        loc='lower left',
        fontsize=12)

    plt.savefig('gpr.png')

最後にガウス過程回帰を実装します。このプログラムでは、初めにカーネル行列$\mathbf{K}$を初期化し、訓練データを用いてカーネル行列$\mathbf{K}$を計算します。その後、それぞれのテストデータに対して、対応するカーネルを計算して、テストデータから回帰した平均と分散を出力します。

def gpr(x_train, y_train, x_test, kernel):
    # average
    mu = []
    # variance
    var = []

    train_length = len(x_train)
    test_length = len(x_test)

    K = np.zeros((train_length, train_length))
    for x_idx in range(train_length):
        for x_prime_idx in range(train_length):
            K[x_idx, x_prime_idx] = kernel(x_train[x_idx], x_train[x_prime_idx])

    yy = np.dot(np.linalg.inv(K), y_train)

    for x_test_idx in range(test_length):
        k = np.zeros((train_length,))
        for x_idx in range(train_length):
            k[x_idx] = kernel(
                x_train[x_idx],
                x_test[x_test_idx])
        s = kernel(
            x_test[x_test_idx],
            x_test[x_test_idx])
        mu.append(np.dot(k, yy))
        kK_ = np.dot(k, np.linalg.inv(K))
        var.append(s - np.dot(kK_, k.T))
    return mu, var


# Radiant Basis Kernel
kernel = lambda x, x_prime : rbf(x, x_prime, theta_1=1.0, theta_2=1.0)
mu, var = gpr(x_train, y_train, x_test, kernel)
plot_gpr(x_train, y_train, x_test, mu, var)

ガウスカーネルを用いると、全てのテストデータに対して、非常に精度良く回帰をすることができていました。

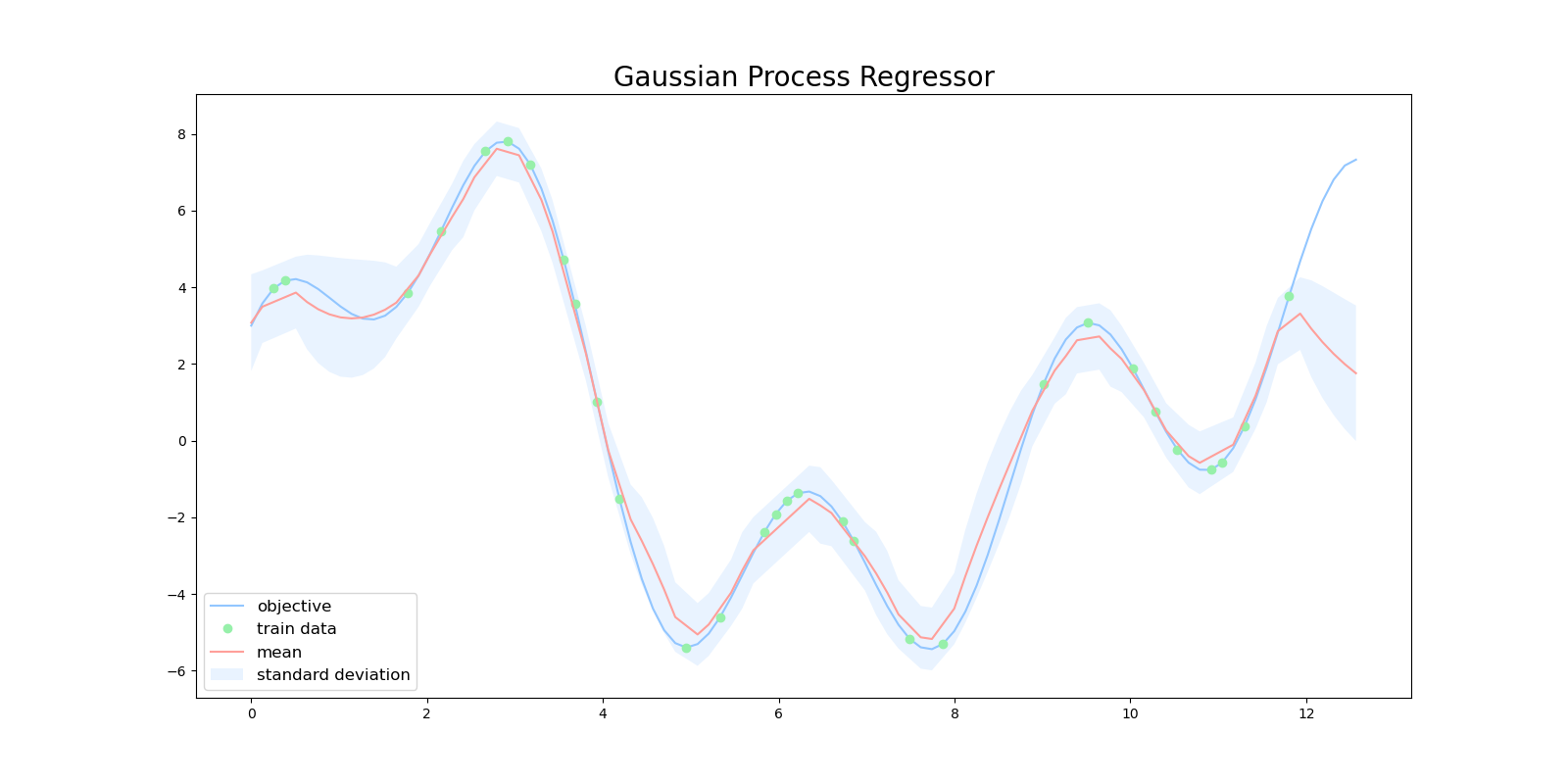
目的関数とカーネルの相性が悪いため、周期カーネルや線形カーネルではうまく回帰できませんでした。

周期カーネル	線形カーネル

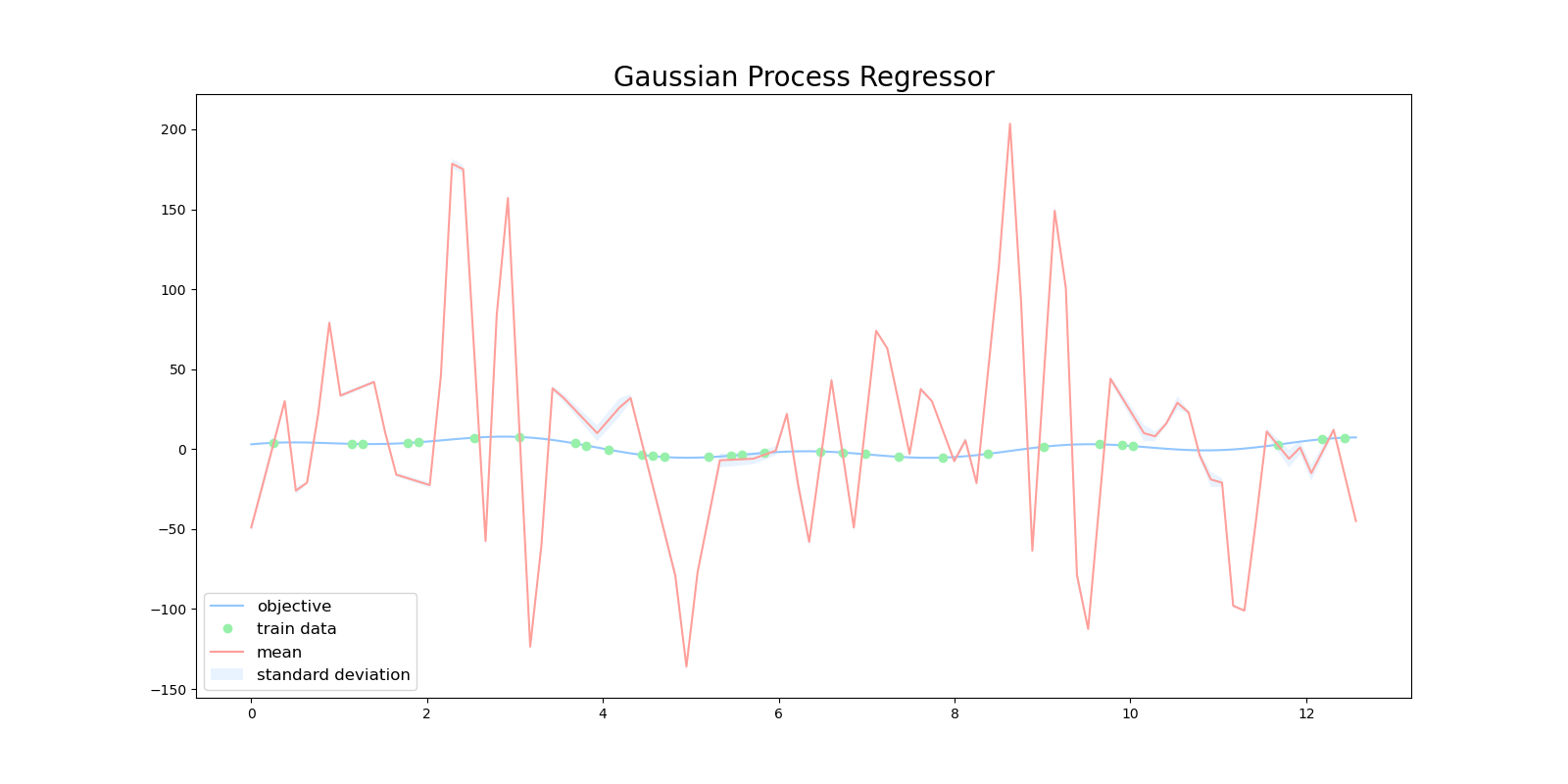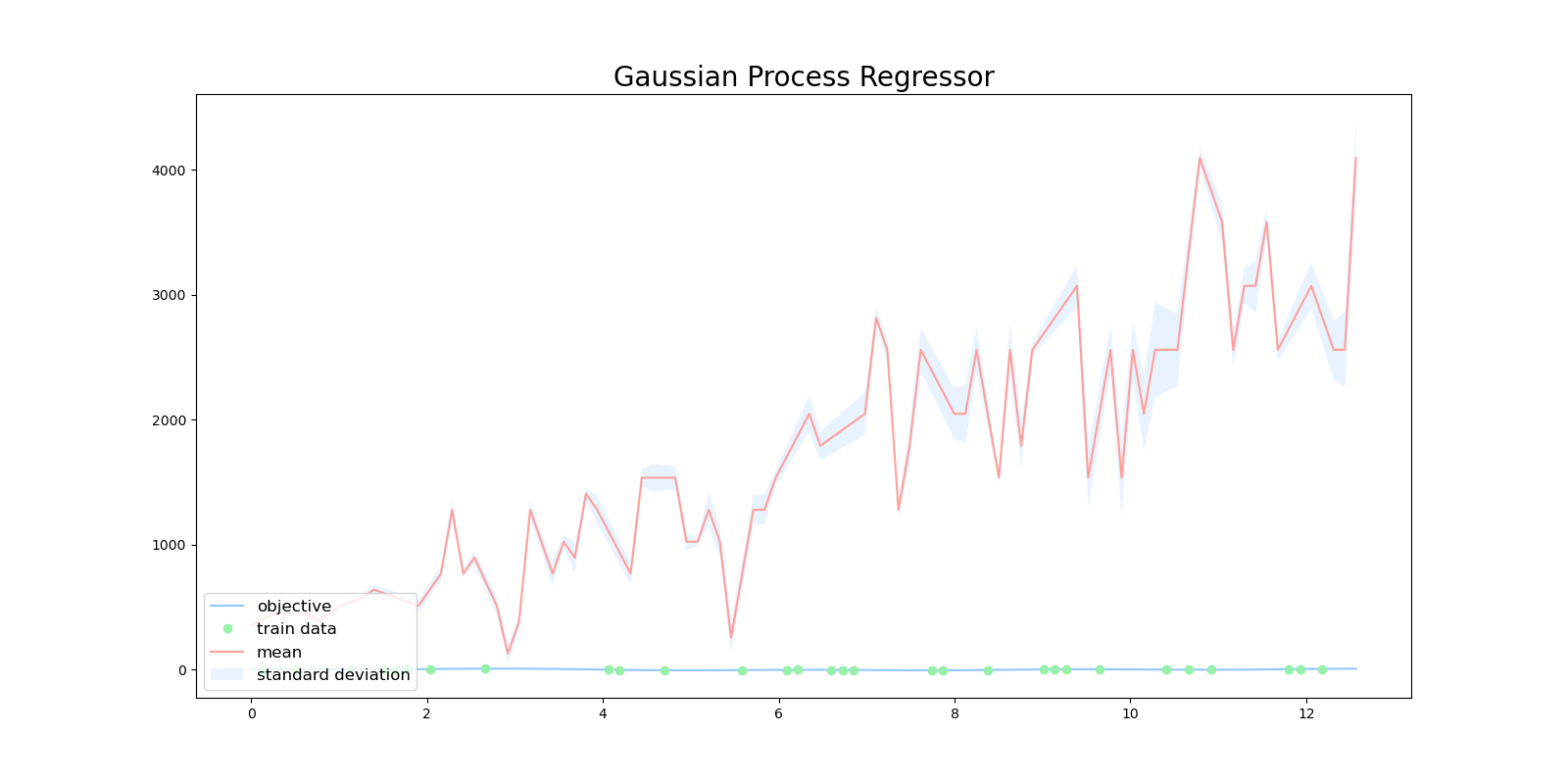指数カーネルを用いるとガウスカーネルほどではないですが、ある程度の精度で回帰をできていました。しかしながら、信頼区間の幅がガウスカーネルに比べて大きく、ガウス過程が回帰結果に対して「自信がなさそう」と考えられます。

まとめ

ガウス過程のプログラムをゼロから自分の手で実装してみました。

ガウスカーネルを用いることで、目的関数をうまく回帰することに成功しました。今回の実験ではガウスカーネルのハイパーパラメータは $\theta_1=1.0$ と $\theta_2=1.0$ を用いています。このハイパーパラメータを用いるとうまく回帰をすることができましたが、毎回このパラメータを探索して見つけ出すのは非常に手間がかかります。

実用的なガウス過程のプログラムでは、モデルの訓練時にカーネルのハイパーパラメータも同時に最適化を行います。この最適化には、MCMCや最尤法を用います。次回の記事では、ガウス過程におけるハイパーパラメータの最適化の実装も行っていこうと思います。

ここまで読んでいただきありがとうございます。

今回実装したコードは全てこちらのレポジトリにあります。