今までに執筆した「ガウス過程 from Scratch」と「ガウス過程 from Scratch MCMCと勾配法によるハイパーパラメータ最適化」では、 ガウス過程(Gaussian Process) をゼロから実装しハイパーパラメータの最適化まで行いました。
前回の記事で行った実験では、ハイパーパラメータが調整されたガウス過程で目的関数をうまく回帰することに成功しました。しかしがら、今まで実装してきたガウス過程ではトータルの計算量として $O(N^3)$ を必要としてしまいます。このままでは $N$ が小さいうちは大きな問題にはなりませんが、 $N$ が大きくなると手に負えなくなってしまいます。
今回の記事では、 コレスキー分解(Cholesky decomposition)$ を用いることでガウス過程の計算量を $O(N^3)$ から $O(N^2)$ まで削減していきます。
※注意
この記事は筆者が勉強したことをまとめて、理解を深めるために執筆しています。内容に誤り等があった場合は、コメント等でご指摘いただけると幸いです。
ガウス過程(Gaussian Process)
どんなN個の入力の集合 $(\mathbf{x_{1}},\mathbf{x_{2}},\dots,\mathbf{x_{N}})$ についても、対応する出力 $(f(\mathbf{x_{1}}),f(\mathbf{x_{2}}),\dots,f(\mathbf{x_{N}}))$ の同時分布 $p(\mathbf{f})$ が、平均 $\mathbf{u}$ と $K_{n{n'}}=k(\mathbf{x_n},\mathbf{x_{n'}})$ を要素とする共分散行列 $\mathbf{K}$ のガウス分布 $\mathbb{N}(\mathbf{u},\mathbf{K})$ に従うとき、 $\mathbf{f}$ は ガウス過程(Gaussian Process) に従うと言います。
\mathbf{f}\sim \textrm{GP}(\mathbf{u},k(\mathbf{x},\mathbf{x'}))
ガウス過程は,ある$\mathbf{x}$に対してスカラー$f(\mathbf{x})$を返すのではなく,$\mathbf{x}$における$f(\mathbf{x})$が従う正規分布の平均と分散を出力します。
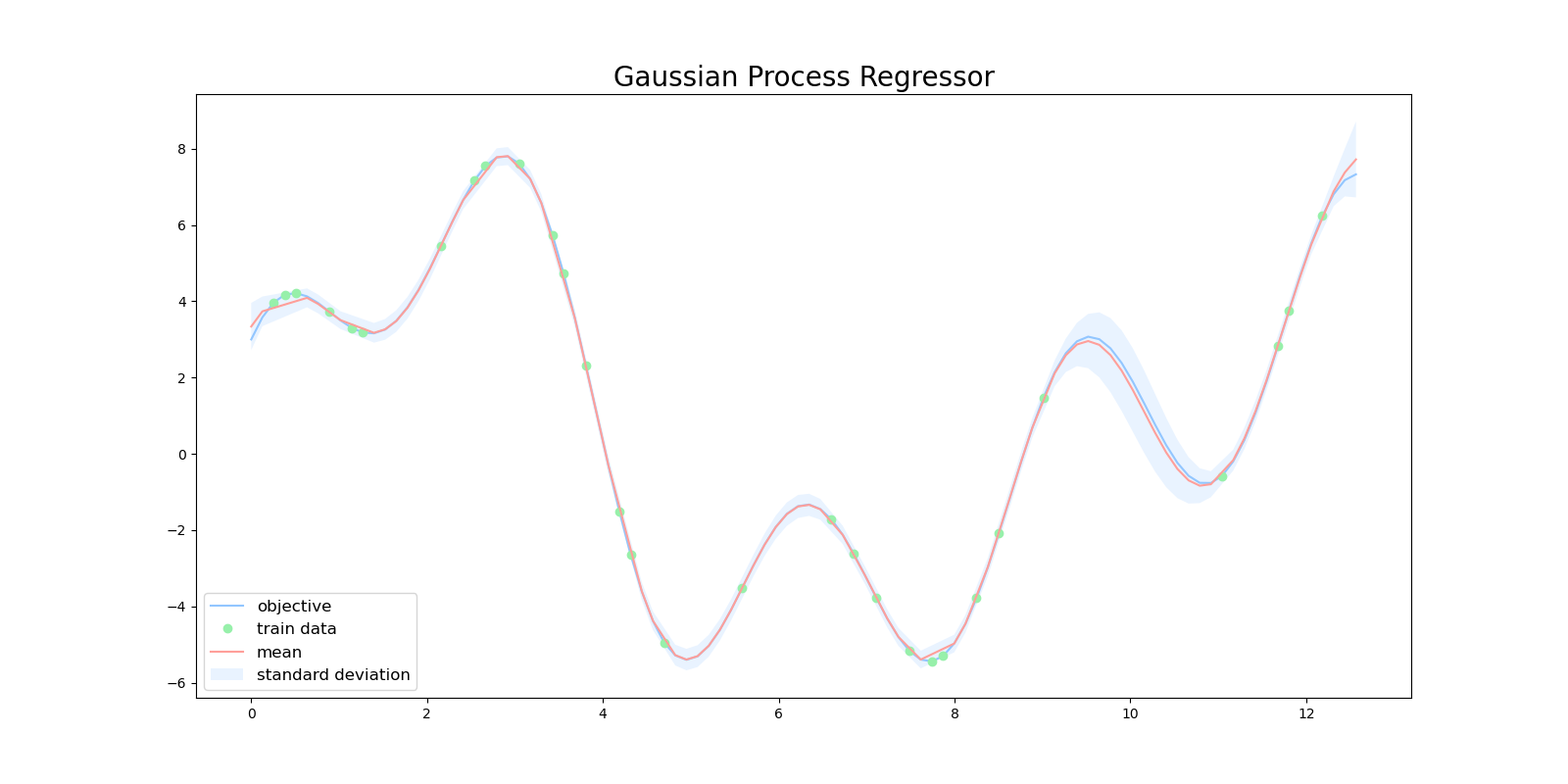
したがって、ガウス過程ではある予測に対する信頼度を表現することができます。下図は、ガウス過程を用いて目的関数を回帰した図になります。緑色の点が学習用データで、赤い線が平均値、水色の領域は全体の95%の信頼区間を表しています。
$x=10$ 周辺に注目すると、この区間では訓練データが少ないため、ガウス過程の出力も自信がない(分散が大きい)ものになっています。
一般的に観測する $y$ にはノイズがのっていることが多いので、
y = f(\mathbf{x})+\epsilon
\epsilon\sim \mathbb{N}(0,\sigma^2)
とするのが自然です。
ノイズを考慮した上でのガウス過程は、 $K_{n{n'}}=k(\mathbf{x_n},\mathbf{x_{n'}})$ を要素とする共分散行列 $\mathbf{K}$ の対角成分に、 $\sigma^2$ を足したものとして表現できます。
k'(\mathbf{x_n},\mathbf{x_{n'}})=k(\mathbf{x_n},\mathbf{x_{n'}})+\sigma^2\delta(n,n')
詳しい解説は前回の記事を参照してください。
コレスキー分解(Cholesky decomposition)
ガウス過程で最も計算量を必要とするのは、カーネル行列 $\mathbf{K}$ の逆行列 $\mathbf{K}^{-1}$ を計算するときです。逆行列 $\mathbf{K}^{-1}$ の計算は、カーネル行列の計算に用いるデータ数を $N$ とすると $O(N^3)$ の計算量オーダーとなります。
カーネル行列を計算するプログラムは例えば次のようになります。このプログラムから明らかなように、計算されたカーネル行列 $\mathbf{K}$ は必ず対称行列になります。一般的にガウス過程では、共分散行列は正定値対称行列でなければならないといった制約が存在します。
def rbf(x, x_prime, theta_1, theta_2):
"""RBF Kernel
Args:
x (float): data
x_prime (float): data
theta_1 (float): hyper parameter
theta_2 (float): hyper parameter
"""
return theta_1 * np.exp(-1 * (x - x_prime)**2 / theta_2)
# Radiant Basis Kernel + Error
def kernel(x, x_prime, theta_1, theta_2, theta_3, noise):
# delta function
if noise:
delta = theta_3
else:
delta = 0
return rbf(x, x_prime, theta_1=theta_1, theta_2=theta_2) + delta
K = np.zeros((N, N))
for x_idx in range(N):
for x_prime_idx in range(N):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], 1.0, 1.0, 1.0, x_idx == x_prime_idx)
行列 $\mathbf{A}$ が正定値対称行列であるとき、 $\mathbf{A}\mathbf{x}=\mathbf{b}$ の解を求める際に高速で数値的に安定な コレスキー分解(Cholesky decomposition) という手法が存在します。
コレスキー分解の重要な点は $\mathbf{A}$ が次式のように $\mathbf{L}$ とその転置 $\mathbf{L}^{\top}$ に分解できるという点です。
\mathbf{A}=\mathbf{L}\mathbf{L}^{\top}
コレスキー分解を用いて $\mathbf{A}$ を分解できると $\mathbf{A}\mathbf{x}=\mathbf{b}$ は次のように計算できます。
\begin{align}
\mathbf{A}\mathbf{x}&=\mathbf{b}\\
\mathbf{L}\mathbf{L}^{\top}\mathbf{x}&=\mathbf{b}\\
\mathbf{L}\mathbf{L}^{\top}\mathbf{x}&=\mathbf{L}\mathbf{y}\quad\textrm{for some }\mathbf{y}\\
\mathbf{L}^{\top}\mathbf{x}&=\mathbf{y}
\end{align}
$\mathbf{L}\mathbf{y}=\mathbf{b}$ を解くことができれば、 $\mathbf{L}^{\top}\mathbf{x}=\mathbf{y}$ を計算することができ、結果として $\mathbf{A}\mathbf{x}=\mathbf{b}$ を満たす解 $\mathbf{x}$ を得ることができます。
$\mathbf{A} \backslash \mathbf{b}$ を $\mathbf{A}\mathbf{x}=\mathbf{b}$ を満たす方程式の解を示す記号だとすると、 $\mathbf{A}\mathbf{x}=\mathbf{b}$ の解は次のように記述することができます。
\mathbf{x} = \mathbf{L}^{\top}\backslash(\mathbf{L}\backslash\mathbf{b})
$\mathbf{L}$ と $\mathbf{L}^{\top}$ は三角行列なので、 後退代入法(backward substitution) や 前進代入法(forward substitution) を用いて、効率的に $\mathbf{L}\mathbf{y}=\mathbf{b}$ や $\mathbf{L}^{\top}\mathbf{x}=\mathbf{y}$ を計算することができます。
例えば、$\mathbf{L}$ が下三角行列だとすると、
\begin{matrix}
l_{11}y_1 & & & &= &b_1 \\
l_{21}y_1 & l_{22}y_2 & & &= &b_2 \\
\vdots & & \ddots & &= &\vdots \\
l_{n1}y_1 & l_{n2}y_2 & \dots & l_{nn}y_n &= &b_n
\end{matrix}
のように表すことができるので、
\begin{align}
y_1 &= \frac{b_1}{l_{11}}\\
y_2 &= \frac{b_2-l_{11}y_1}{l_{22}}\\
\vdots
\end{align}
と順次計算することができます。
コレスキー分解 $\mathbf{L}\mathbf{L}^{\top}=\mathbf{A}$ による、方程式 $\mathbf{A}\mathbf{A}^{-1}=\mathbf{I}$ の計算は $O(N^{2})$ で行うことができます。
コレスキー分解によるガウス過程の高速化
$\mathbf{f}\sim \textrm{GP}(\mathbf{0},k'(\mathbf{x},\mathbf{x'}))$ のとき、データに含まれない $\mathbf{x*}$ による $y*$ の予測値は、 $\mathbf{y}$ に $y*$ を含めた全体がまたガウス分布に従うことから
\begin{pmatrix}\mathbf{y} \\ y^{*} \end{pmatrix}{\sim}N(\mathbf{0},
\begin{pmatrix}
\mathbf{K} & \mathbf{k_*} \\
\mathbf{k_*^T} & k_{**}
\end{pmatrix}
+ \sigma^2\mathbf{I}
)
とすることで、ガウス分布の性質を用いて計算することができます。
P(y^{*}{\mid}\mathbf{x^*}, D)=\mathbb{N}(\mathbf{k_*^T}(\mathbf{K}+\sigma^2\mathbf{I})^{-1}\mathbf{y},k_{**}-\mathbf{k_*^T}(\mathbf{K}+\sigma^2\mathbf{I})^{-1}\mathbf{k})
D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),\dots,(\mathbf{x_N},y_N)\}
このとき、事後分布の計算は、コレスキー分解を用いて
\mathbf{L}=\textrm{cholesky}(\mathbf{K}+\sigma^2 \mathbf{I})
\boldsymbol \alpha=\mathbf{L}^{\top}\backslash (\mathbf{L}\backslash\mathbf{y})
\mathbf{u}_{*}=\mathbf{k}_{*}^{\top}\boldsymbol \alpha
\mathbf{v}=L\backslash\mathbf{k}_{*}
\mathbf{\Sigma}_{*}=k(\mathbf{x}_{*},\mathbf{x}_{*})-\mathbf{v}^{\top}\mathbf{v}
とすることで、高速に計算することができます。
少し複雑で理解し難いので一つ一つ見ていきます。 $\mathbf{A}=\mathbf{K}+\sigma^{2}\mathbf{I}$ とすると、逆行列 $\mathbf{A}^{-1}$ を計算するには方程式 $\mathbf{A}\mathbf{A^{-1}}=\mathbf{I}$ を解く必要があります。
したがって、コレスキー分解を用いると
\mathbf{A}^{-1}=\mathbf{L}^{\top}\backslash (\mathbf{L}\backslash \mathbf{I})
として計算することができます。
ここで、方程式 $\mathbf{A}\mathbf{A^{-1}}=\mathbf{I}$ の両辺に $\mathbf{y}$ をかけると、
\begin{align}
\mathbf{A}\mathbf{A}^{-1}\mathbf{y}&=\mathbf{I}\mathbf{y}\\
\mathbf{L}\mathbf{L}^{\top}\mathbf{A}^{-1}\mathbf{y}&=\mathbf{y}\\
\mathbf{L}\mathbf{L}^{\top}\mathbf{x}&=\mathbf{L}\mathbf{T}\mathbf{y}\quad\textrm{for some }\mathbf{T}\\
\mathbf{L}^{\top}\mathbf{A}^{-1}\mathbf{y}&=\mathbf{T}\mathbf{y}
\end{align}
であり、
\begin{align}
\mathbf{A}^{-1}\mathbf{y}&=\mathbf{L}^{\top}\backslash \mathbf{T}\mathbf{y}\\
&=\mathbf{L}^{\top}\backslash (\mathbf{L}\backslash\mathbf{y})
\end{align}
と変形することができます。
計算の見通しを良くするために、 $\boldsymbol\alpha=\mathbf{A}^{-1}\mathbf{y}$ とすると
\boldsymbol \alpha=\mathbf{A}^{-1}\mathbf{y}\quad\Rightarrow\quad\mathbf{k}_{*}^{\top}\boldsymbol \alpha=\mathbf{k}_{*}^{\top}\mathbf{A}^{-1}\mathbf{y}=\mathbf{u}_{*}
として、ガウス分布の平均を計算することができます。
ガウス分布の分散もコレスキー分解を用いて計算できます。 $\mathbf{v}=\mathbf{L}\backslash\mathbf{k}_{*}$ とすると、
\mathbf{L}\mathbf{v}=\mathbf{k}_{*}
\mathbf{v}^{-1}=L^{-1}\mathbf{k}_{*}
\begin{align}
\mathbf{v}^{\top}&=(L^{-1}\mathbf{k}_{*})^{\top}\\
&=\mathbf{k}_{*}^{\top}(L^{\top})^{-1}
\end{align}
となります。
したがって、
\begin{align}
\mathbf{v}^{\top}\mathbf{v}&=\mathbf{k}_{*}^{\top}(L^{\top})^{-1} L^{-1}\mathbf{k}_{*}\\
&=\mathbf{k}_{*}^{\top}(L^{\top}L)^{-1}\mathbf{k}_{*}\\
&=\mathbf{k}_{*}^{\top}A^{-1}\mathbf{k}_{*}
\end{align}
\begin{align}
k(\mathbf{x}_{*},\mathbf{x}_{*})-\mathbf{v}^{\top}\mathbf{v}&=k(\mathbf{x}_{*},\mathbf{x}_{*})-\mathbf{k}_{*}^{\top}A^{-1}\mathbf{k}_{*}\\
&=\mathbf{\Sigma}_{*}
\end{align}
と計算することで、ガウス分布の分散を得ることができます。
コレスキー分解を用いて高速化したガウス過程を実装していきます。コレスキー分解はscipyのパッケージからインポートしたものを使います。
from scipy.linalg import cholesky, cho_solve
def gpr(x_train, y_train, x_test):
# average
mu = []
# variance
var = []
train_length = len(x_train)
test_length = len(x_test)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], thetas[0], thetas[1], thetas[2], x_idx == x_prime_idx)
L_ = cholesky(K, lower=True)
alpha_ = cho_solve((L_, True), y_train)
for x_test_idx in range(test_length):
k = np.zeros((train_length,))
for x_idx in range(train_length):
k[x_idx] = kernel(
x_train[x_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_idx == x_test_idx)
s = kernel(
x_test[x_test_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_test_idx == x_test_idx)
v_ = cho_solve((L_, True), k.T)
mu.append(np.dot(k, alpha_))
var.append(s - np.dot(k, v_))
return np.array(mu), np.array(var)
\begin{align}
\mathbf{A}^{-1}\mathbf{y}&=\mathbf{L}^{\top}\backslash \mathbf{T}\mathbf{y}\\
&=\mathbf{L}^{\top}\backslash (\mathbf{L}\backslash\mathbf{y})
\end{align}
この計算はプログラムの次の部分に対応します。
L_ = cholesky(K, lower=True)
alpha_ = cho_solve((L_, True), y_train)
scipyからインポートされたcho_solveでは、 $\mathbf{A}$ をコレスキー分解された行列として、方程式 $\mathbf{A}\mathbf{x}=\mathbf{b}$ を解きます。
cho_solveの引数に対して、Trueを渡すと $\mathbf{A}$ が下三角行列であることを、Falseを渡すと $\mathbf{A}$ が上三角行列であることを示します。
\mathbf{k}_{*}^{\top}\boldsymbol \alpha=\mathbf{k}_{*}^{\top}\mathbf{A}^{-1}\mathbf{y}=\mathbf{u}_{*}
\begin{align}
k(\mathbf{x}_{*},\mathbf{x}_{*})-\mathbf{v}^{\top}\mathbf{v}&=k(\mathbf{x}_{*},\mathbf{x}_{*})-\mathbf{k}_{*}^{\top}A^{-1}\mathbf{k}_{*}\\
&=\mathbf{\Sigma}_{*}
\end{align}
この計算はプログラムの次の部分に対応します。
for x_test_idx in range(test_length):
k = np.zeros((train_length,))
for x_idx in range(train_length):
k[x_idx] = kernel(
x_train[x_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_idx == x_test_idx)
s = kernel(
x_test[x_test_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_test_idx == x_test_idx)
v_ = cho_solve((L_, True), k.T)
mu.append(np.dot(k, alpha_))
var.append(s - np.dot(k, v_))
コレスキー分解によるログ尤度の計算
$\mathbf{y}\sim\mathbb{N}(\mathbf{0},\mathbf{K}+\sigma^2\mathbf{I})$ のとき、前回の記事よりログ尤度は
\log{P(\mathbf{y}|\mathbf{X})}=-\frac{n}{2}\log{(2\pi)}-\frac{1}{2}\log{\textrm{det}(\mathbf{K}+\sigma^2\mathbf{I})}-\frac{1}{2}\mathbf{y}^T(\mathbf{K}+\sigma^2\mathbf{I})^{-1}\mathbf{y}
と表すことができます。
今までの議論より、コレスキー分解を用いると
-\frac{1}{2}\mathbf{y}^T(\mathbf{K}+\sigma^2\mathbf{I})^{-1}\mathbf{y}=-\frac{1}{2}\mathbf{y}^T\boldsymbol \alpha
となります。
また、 $\textrm{det}(\mathbf{K}+\sigma^2\mathbf{I})$ について
\textrm{det}(\mathbf{K}+\sigma^2\mathbf{I}) = \textrm{det}(\mathbf{L}\mathbf{L}^{\top}) = \textrm{det}(\mathbf{L})\textrm{det}(\mathbf{L}^{\top})
と変形することができます。 $\mathbf{L}$ と $\mathbf{L}^{\top}$ は三角行列で対角成分は共通なので、それらの行列式は対角成分の積のみになります。
\textrm{det}(\mathbf{L})=\textrm{det}(\mathbf{L}^{\top})=\prod_{i=1}^n l_{i,i}
したがって、
\begin{align}
\log\textrm{det}(\mathbf{K}+\sigma^2\mathbf{I})&=\log\textrm{det}(\mathbf{L})^2\\
&=\log ((\prod_{i=1}^n l_{i,i})^2)\\
&=2\sum_{i=1}^{n}\log l_{i,i}
\end{align}
と計算することができます。
コレスキー分解を用いると、ガウス過程のログ尤度は次のように表すことができます。
\log{P(\mathbf{y}|\mathbf{X})}=-\frac{n}{2}\log{(2\pi)}-\sum_{i=1}^{n}\log l_{i,i}-\frac{1}{2}\mathbf{y}^T\boldsymbol \alpha
コレスキー分解を用いたログ尤度を計算するプログラムを実装していきます。特に難しい実装はなく式をそのままプログラムに書き起こすだけです。
def log_marginal_likelihood(params):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], params[0], params[1], params[2], x_idx == x_prime_idx)
L_ = cholesky(K, lower=True)
alpha_ = cho_solve((L_, True), y_train)
return - 0.5 * np.dot(y_train.T, alpha_) - np.sum(np.log(np.diag(L_))) - 0.5 * train_length * np.log(2 * np.pi)
コレスキー分解による勾配の計算
$\mathbf{y}\sim\mathbb{N}(\mathbf{0},\mathbf{K}+\sigma^2\mathbf{I})$ のとき、同様に前回の記事よりログ尤度をカーネルのハイパーパラメータ $\mathbf{\theta}$ で微分した式は
\frac{\partial}{\partial\boldsymbol{\theta}}\log{P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})}=-\frac{1}{2}\mathrm{tr}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}})+\frac{1}{2}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\mathbf{y})^{\top}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\mathbf{y})
と表すことができます。
2次形式の公式 $\mathbf{x}^{\top}\mathbf{A}\mathbf{x}=\mathrm{tr}(\mathbf{x}\mathbf{x}^{\top}\mathbf{A})$ を用いると、
\begin{align}
\frac{\partial}{\partial\boldsymbol{\theta}}\log{P(\mathbf{y}|\mathbf{X},\boldsymbol{\theta})}&=-\frac{1}{2}\mathrm{tr}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}})+\frac{1}{2}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\mathbf{y})^{\top}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\mathbf{y})\\
&=-\frac{1}{2}\mathrm{tr}(\mathbf{K}_{\boldsymbol{\theta}}^{-1}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}})+\frac{1}{2}\boldsymbol\alpha^{\top}\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}}\boldsymbol\alpha\\
&=\frac{1}{2}\mathrm{tr}((\boldsymbol\alpha\boldsymbol\alpha^{\top}-\mathbf{K}_{\boldsymbol{\theta}}^{-1})\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}})
\end{align}
と計算することができます。
コレスキー分解を用いた勾配を計算するプログラムを実装していきます。
def log_likelihood_gradient(params):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
dK_dTheta = np.zeros((3, train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
k, grad = kernel(x_train[x_idx], x_train[x_prime_idx], params[0],
params[1], params[2], x_idx == x_prime_idx, eval_grad=True)
K[x_idx, x_prime_idx] = k
dK_dTheta[0, x_idx, x_prime_idx] = grad[0]
dK_dTheta[1, x_idx, x_prime_idx] = grad[1]
dK_dTheta[2, x_idx, x_prime_idx] = grad[2]
L_ = cholesky(K, lower=True)
alpha_ = cho_solve((L_, True), y_train)
K_inv = cho_solve((L_, True), np.eye(K.shape[0]))
inner_term = np.einsum("i,j->ij", alpha_, alpha_) - K_inv
inner_term = np.einsum("ij,kjl->kil", inner_term, dK_dTheta)
return 0.5 * np.einsum("ijj", inner_term)
上記のプログラムではnp.einsum()という関数が使われています。np.einsum()はアインシュタインの縮約記法と呼ばれる記法で計算をする方法です。詳しく知りたい人はこちらの記事が参考になると思います。
\frac{1}{2}\mathrm{tr}((\boldsymbol\alpha\boldsymbol\alpha^{\top}-\mathbf{K}_{\boldsymbol{\theta}}^{-1})\frac{\partial\mathbf{K}_{\boldsymbol{\theta}}}{\partial\boldsymbol{\theta}})
この計算がプログラムの次の部分に対応しています。
inner_term = np.einsum("i,j->ij", alpha_, alpha_) - K_inv
inner_term = np.einsum("ij,kjl->kil", inner_term, dK_dTheta)
return 0.5 * np.einsum("ijj", inner_term)
アインシュタインの縮約記法を使うことで、複雑な行列の計算を簡潔に記述することができます。
全体のプログラム
ハイパーパラメータの最適化まで含めた全体のプログラムは次の通りになります。ハイパーパラメータの最適化には勾配法を用いていますが、高速化したログ尤度の計算を用いてMCMCで最適化を行うこともできます。
import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize
from scipy.linalg import cholesky, cho_solve
plt.style.use('seaborn-pastel')
def objective(x):
return 2 * np.sin(x) + 3 * np.cos(2 * x) + 5 * np.sin(2 / 3 * x)
def rbf(x, x_prime, theta_1, theta_2):
"""RBF Kernel
Args:
x (float): data
x_prime (float): data
theta_1 (float): hyper parameter
theta_2 (float): hyper parameter
"""
return theta_1 * np.exp(-1 * (x - x_prime)**2 / theta_2)
def train_test_split(x, y, test_size):
assert len(x) == len(y)
n_samples = len(x)
test_indices = np.sort(
np.random.choice(
np.arange(n_samples), int(
n_samples * test_size), replace=False))
train_indices = np.ones(n_samples, dtype=bool)
train_indices[test_indices] = False
test_indices = ~ train_indices
return x[train_indices], x[test_indices], y[train_indices], y[test_indices]
n = 100
data_x = np.linspace(0, 4 * np.pi, n)
data_y = objective(data_x)
x_train, x_test, y_train, y_test = train_test_split(
data_x, data_y, test_size=0.70)
def plot_gpr(x_train, y_train, x_test, mu, var):
plt.figure(figsize=(16, 8))
plt.title('Gradient Decent', fontsize=20)
plt.plot(data_x, data_y, label='objective')
plt.plot(
x_train,
y_train,
'o',
label='train data')
std = np.sqrt(np.abs(var))
plt.plot(x_test, mu, label='mean')
plt.fill_between(
x_test,
mu + 2 * std,
mu - 2 * std,
alpha=.2,
label='standard deviation')
plt.legend(
loc='lower left',
fontsize=12)
plt.savefig('gpr.png')
# Radiant Basis Kernel + Error
def kernel(x, x_prime, theta_1, theta_2, theta_3, noise, eval_grad=False):
# delta function
if noise:
delta = theta_3
else:
delta = 0
if eval_grad:
dk_dTheta_1 = kernel(x, x_prime, theta_1, theta_2, theta_3, noise) - delta
dk_dTheta_2 = (kernel(x, x_prime, theta_1, theta_2, theta_3, noise) - delta) * ((x - x_prime)**2) / theta_2
dk_dTheta_3 = delta
return rbf(x, x_prime, theta_1=theta_1, theta_2=theta_2) + \
delta, np.array([dk_dTheta_1, dk_dTheta_2, dk_dTheta_3])
return rbf(x, x_prime, theta_1=theta_1, theta_2=theta_2) + delta
def optimize(x_train, y_train, bounds, initial_params=np.ones(3)):
bounds = np.atleast_2d(bounds)
def log_marginal_likelihood(params):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], params[0], params[1], params[2], x_idx == x_prime_idx)
L_ = cholesky(K, lower=True)
alpha_ = cho_solve((L_, True), y_train)
return - 0.5 * np.dot(y_train.T, alpha_) - np.sum(np.log(np.diag(L_))) - 0.5 * train_length * np.log(2 * np.pi)
def log_likelihood_gradient(params):
train_length = len(x_train)
K = np.zeros((train_length, train_length))
dK_dTheta = np.zeros((3, train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
k, grad = kernel(x_train[x_idx], x_train[x_prime_idx], params[0],
params[1], params[2], x_idx == x_prime_idx, eval_grad=True)
K[x_idx, x_prime_idx] = k
dK_dTheta[0, x_idx, x_prime_idx] = grad[0]
dK_dTheta[1, x_idx, x_prime_idx] = grad[1]
dK_dTheta[2, x_idx, x_prime_idx] = grad[2]
L_ = cholesky(K, lower=True)
alpha_ = cho_solve((L_, True), y_train)
K_inv = cho_solve((L_, True), np.eye(K.shape[0]))
inner_term = np.einsum("i,j->ij", alpha_, alpha_) - K_inv
inner_term = np.einsum("ij,kjl->kil", inner_term, dK_dTheta)
return 0.5 * np.einsum("ijj", inner_term)
def obj_func(params):
lml = log_marginal_likelihood(params)
grad = log_likelihood_gradient(params)
return -lml, -grad
opt_res = scipy.optimize.minimize(
obj_func,
initial_params,
method="L-BFGS-B",
jac=True,
bounds=bounds,
)
theta_opt, func_min = opt_res.x, opt_res.fun
return theta_opt, func_min
def gpr(x_train, y_train, x_test):
# average
mu = []
# variance
var = []
train_length = len(x_train)
test_length = len(x_test)
thetas, _ = optimize(x_train, y_train, bounds=np.array(
[[1e-2, 1e2], [1e-2, 1e2], [1e-2, 1e2]]), initial_params=np.array([0.5, 0.5, 0.5]))
print(thetas)
K = np.zeros((train_length, train_length))
for x_idx in range(train_length):
for x_prime_idx in range(train_length):
K[x_idx, x_prime_idx] = kernel(
x_train[x_idx], x_train[x_prime_idx], thetas[0], thetas[1], thetas[2], x_idx == x_prime_idx)
L_ = cholesky(K, lower=True)
alpha_ = cho_solve((L_, True), y_train)
for x_test_idx in range(test_length):
k = np.zeros((train_length,))
for x_idx in range(train_length):
k[x_idx] = kernel(
x_train[x_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_idx == x_test_idx)
s = kernel(
x_test[x_test_idx],
x_test[x_test_idx], thetas[0], thetas[1], thetas[2], x_test_idx == x_test_idx)
v_ = cho_solve((L_, True), k.T)
mu.append(np.dot(k, alpha_))
var.append(s - np.dot(k, v_))
return np.array(mu), np.array(var)
if __name__ == "__main__":
mu, var = gpr(x_train, y_train, x_test)
plot_gpr(x_train, y_train, x_test, mu, var)
まとめ
ガウス過程の出力の計算とハイパーパラメータ最適化の計算をコレスキー分解を用いることで高速化しました。
コレスキー分解を用いる前は $O(N^3)$ だった計算量がコレスキー分解を用いた後は $O(N^2)$ の計算量に落ち着きました。
今まではデータ数が多くなるとすぐに対応できなくなっていましたが、 $O(N^2)$ まで計算量を抑えたことである程度のデータ数までならガウス過程を用いて計算できるようになりました。
ここまでの実装でscikit-learnのGaussianProcessRegressorと同程度のパフォーマンスを発揮できます。
次回以降の記事では、疎ガウス過程やガウス過程による潜在変数モデルを扱ってみたいと思います。
ここまで読んでいただきありがとうございます。
今回実装したコードは全てこちらのレポジトリにあります。
参考文献
[1] C. E. Rasmussen and C. K. I. Williams. Gaussian Processes for Machine Learning. 2006.
[2] Jaehoon Lee, Yasaman Bahri. Deep Neural Networks as Gaussian Processes. 2018.
[3] Robert B. Gramacy. Gaussian Process Modeling, Design and Optimization for the Applied Science. 2021.
[4] 持橋 大地, ガウス過程と機械学習. 2019.