ランダムフォレストとは?
決定木はデータを分割して予測するが、1本だけだと過学習しやすい欠点がある。この欠点を克服するのがランダムフォレストである。ランダムフォレストは、分類や回帰に使われるアンサンブル学習手法の一つである。簡単に言えば「たくさんの決定木を作って、その多数決(分類)や平均(回帰)で予測する」方法である。
アンサンブル手法
分類
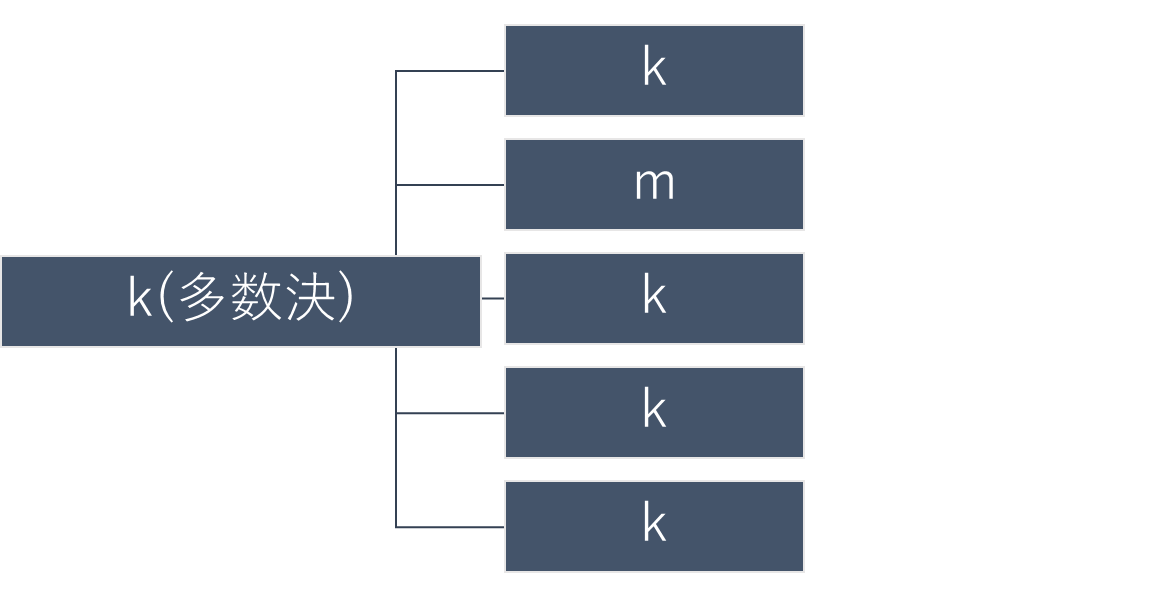
上記のように5つの決定木から多数決で決めるバギングというアンサンブル手法である。ブートストラップと言われる、重複を許してランダムに特徴量の選択を通して決定木を並列に作成する。この図においては、この並列した木に任意の変数$x$をインプットしたときに各木の結果は$kまたはm$となる。ランダムフォレストは、多数決によって$k$を予測値とする仕組みである。なお、数式では以下の通りに一行で示すことができる。
\hat{y}(\mathbf{x}) = \arg\max_k \sum_{m=1}^M \mathbf{1}[f_m(\mathbf{x}) = k]
わざわざ数式をひっぱりだす意味もないが、個人的な理解のために記載する。この式の意味するとこは要するに「各クラスごとに木の数を数えて、一番多いクラスを最終予測にする」ということである。
記号の意味
- $M$:木の本数(ランダムフォレストの中にある決定木の数)
- $f_m(\mathbf{x})$: $m$ 番目の決定木の予測クラスラベル
- $\mathbf{1}[\cdot]$:インジケータ関数(条件が真なら1、偽なら0を返す)
- $arg\max_k$:一番多くの木に選ばれたクラス
式を文章にすると
- 入力 $\mathbf{x}$ に対して、すべての木 $f_1, f_2, \dots, f_M$ がそれぞれクラスを予測する
- 「クラス $k$ を予測した木の数」を$\sum_{m=1}^M \mathbf{1}[f_m(\mathbf{x})=k]$で数える
- その中で一番多くの木に選ばれたクラス$(arg\max_𝑘)$を最終予測$\hat{𝑦}$とする
具体例
木が3本あり、入力$x$に対する予測が
木1 → 「赤」
木2 → 「青」
木3 → 「赤」
だったとする。このとき各クラスのカウントは
「赤」: 2
「青」: 1
となるので、$arg\max$をとると「赤」が最終予測となる。
回帰
回帰の場合は以下の式で示すことができる。回帰では各決定木の予測値の単純平均をとる。
\hat{y}(\mathbf{x}) = \frac{1}{M} \sum_{m=1}^M f_m(\mathbf{x})
- $f_m(\mathbf{x})$: $m$ 本目の決定木の予測値
- $M$:木の本数
ハイパーパラメータ
-
n_estimators:木の本数。多いほど安定するが計算コストが上がる -
max_features:各分割で参照する特徴量数。小さくすると木間相関が下がりやすい。基本デフォルト
(ブートストラップでは特徴量のデータ数(行)をいくらか削っていた。こちらはブートストラップした特徴量に対して、さらに説明変数(列)を削るイメージ) -
max_depth,min_samples_leaf:木の複雑さを制御し、過学習を抑える -
bootstrap:通常はTrue(ブートストラップ有効)

まとめ
決定木を理解していると、理論的には学ぶべきところは少ない。割とすぐに記事を完成できた気がする。
- たくさんの木を独立に近づけて育て、まとめて予測するのがランダムフォレストである
- 多数決・平均により、過学習を抑えられる
- ハイパーパラメータは「木の数」「特徴量サブサンプル」「深さ制御」がポイントになる