統計検定2級の学習記録を付けようと思います。
1.1 変数の分類
- 変数は質的変数と量的変数に分類される
- 質的変数は名義尺度と順序尺度、量的変数は感覚尺度と比例尺度に分かれる
- 量的変数は連続変数もしくは離散変数に分類される
1.2 量的データの分布
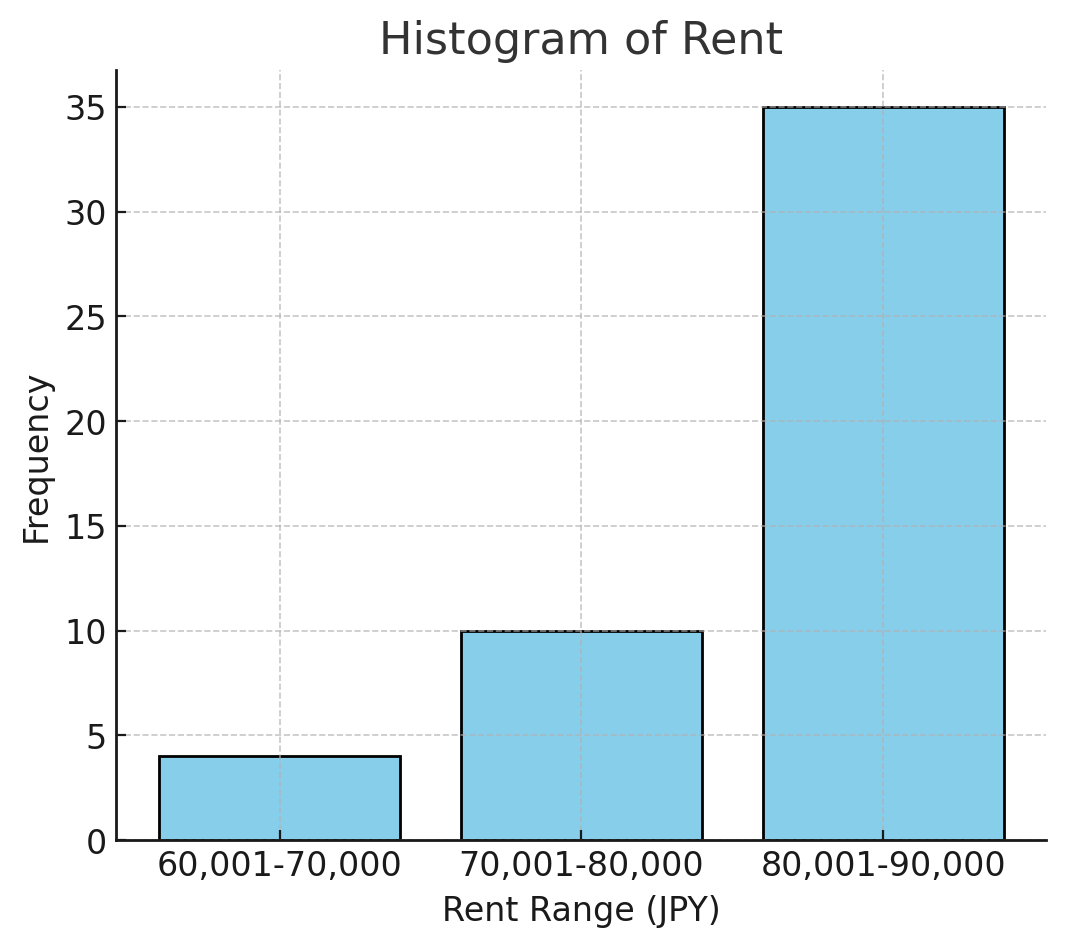
ヒストグラムの作り方
- 度数分布表を作成する。階級の数、階級幅を決める。
| 家賃 | 度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|
| 60,001~70,000 | 4 | 0.08 | 0.08 |
| 70,001~80,000 | 10 | 0.20 | 0.28 |
| 80,001~90,000 | 35 | 0.72 | 1.00 |
棒グラフとヒストグラムの違い:
棒グラフは質的変数が適用、ヒストグラフは量的変数が適用。
棒グラフは度数を高さ、ヒストグラムは度数を面積で示す。また、上図は棒の間隔が空いているが本当は空けてはならない。(pythonライブラリの仕様です)
幹葉図
下図であれば、幹6には、60000, 62000, 63000, 64000が含んでいる。
| 幹(万) | 葉(千) | 度数 |
|---|---|---|
| 6 | 0234 | 0.08 |
| 7 | 0035677888 | 0.20 |
| 8 | 0000111112222333334… | 0.72 |
累積分布図
データを小さい順に並べて、横軸に値を、縦軸にその値以下の値を示した個体の全数に対する割合(累積相対度数など)を示す。
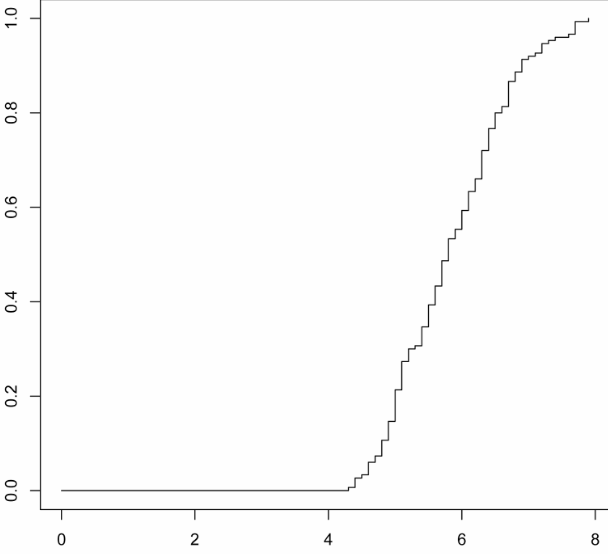
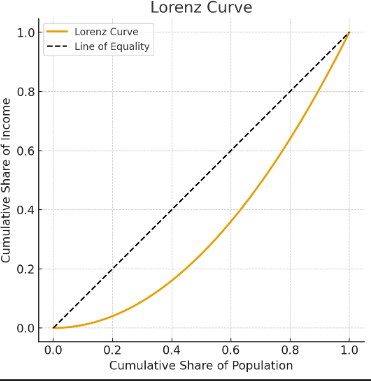
ローレンツ曲線
傾き1の直線は完全平等線、下にへこむほど不平等を示す。
作図方法
1)世帯を所得の低い順に並べる、2)世帯を階級で分け、各階級の世帯の度数と総所得を計算、3)階級ごとに世帯数と全所得額の累積相対度数を計算。
1.3 分布の特徴を表す指標
標準化得点
この変換は値全体の平均0、標準偏差1にする。
標準化得点 = \frac{個々の観測値-平均}{標準偏差}=\frac{x_i-\bar{x}}{s}
変動係数
平均が異なるデータの散らばり方を比較する指標
変動係数CV = \frac{標準偏差}{平均}=\frac{s}{\bar{x}}
中央値・最頻値
中央値(median): 観測値を小さい順に並べて、ちょうど真ん中に位置する観測値
最頻値(mode): 最も多く観測された観測値
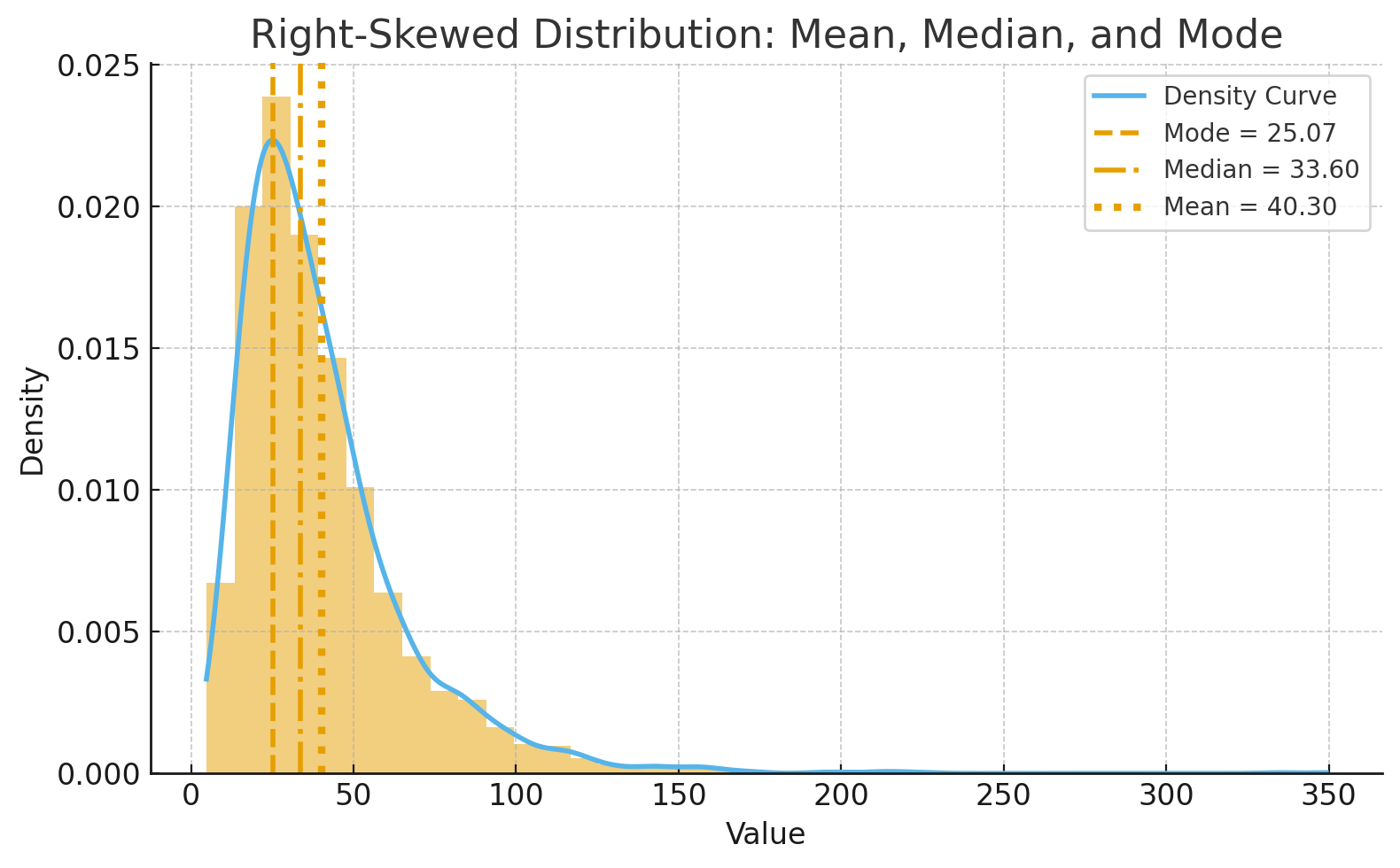
四分位範囲
累積相対度数分布における25%、50%、75%の値を第1四分位数、第2四分位数(中央値)、第3四分位数と呼ぶ。
また四分位範囲IQRは$IQR=O3-Q1$で示す。
1.4 量的データの要約とグラフ表現
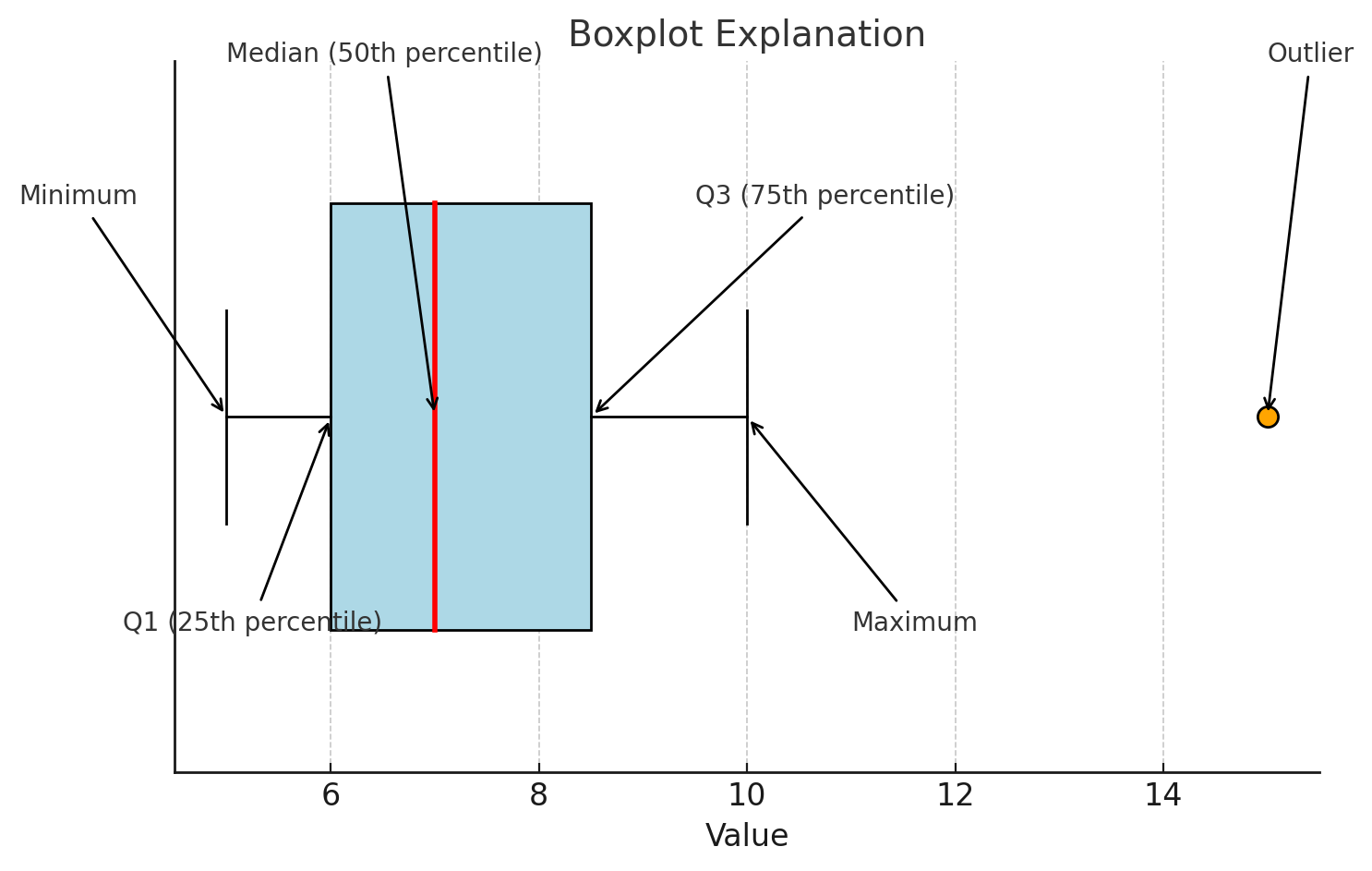
箱ひげ図
最小値、最大値、第1四分位数、第2四分位数(中央値)、第3四分位数で示す図。箱ひげ図の特徴は、ヒストグラムと比較して、中央値や分布の歪み、外れ値が視覚的に分かる。なお、最大値は$Q3+1.5×IQR$、最小値を$Q1-1.5×IQR$として、それに含まれない値を外れ値とするのが主流。
1.5 質的データの度数分布とグラフ表現
相関係数
相関係数を理解するために、まず共分散$s_{xy}$の定義を示す。
s_{xy} = \frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})
共分散の正負は$(\bar{x},\bar{y})$を原点(データの重心)としたグラフにおいて、共に$(x_i-\bar{x}), (y_i-\bar{y})$が正または負のとき共分散は正に近づく、いずれかが負であれば共分散は負に近づく(下図)。結果的に共分散が正であれば正の相関、負であれば負の相関を意味する。
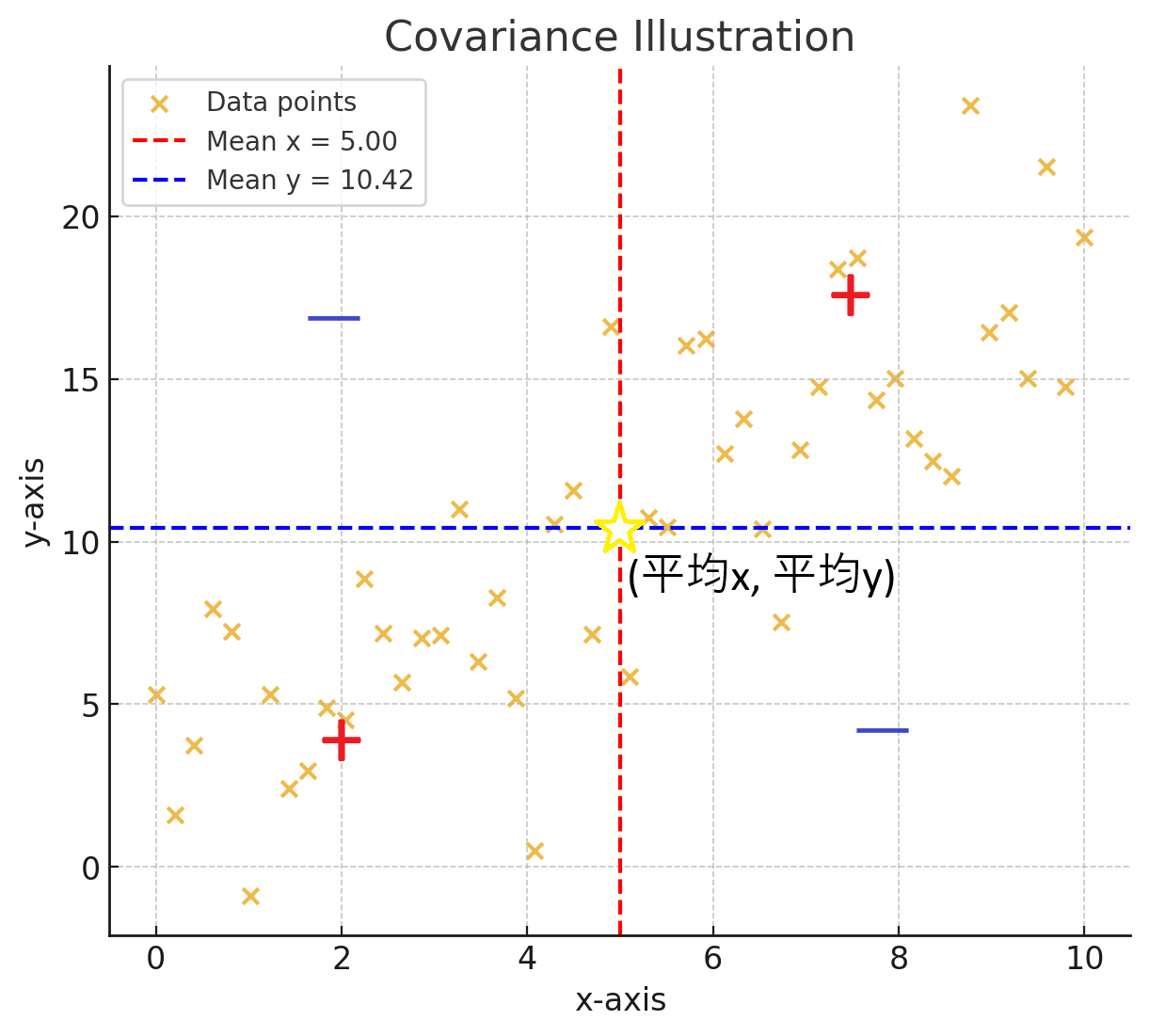
しかし、共分散はばらつきによって大きさが変わるため、$xとy$の標準偏差で割る。これを**相関係数(ピアソンの積率相関係数)$R$**と言う。下記式の通り、標準化得点同士の共分散と解釈できる。
R = \frac{s_{xy}}{s_xs_y}=\frac{1}{n}\sum_{i=1}^{n}\frac{(x_i-\bar{x})}{s_x}\frac{(y_i-\bar{y})}{s_y}
偏相関係数
偏相関係数は「他の変数の影響を取り除いた後の相関」である。
例えば 3 変数 (X, Y, Z) の場合:
r_{XY \cdot Z} = \operatorname{corr}(u_x, u_y)
= \frac{\operatorname{cov}(u_x, u_y)}
{\sqrt{\operatorname{var}(u_x)\operatorname{var}(u_y)}}=\frac{r_{XY} - r_{XZ}r_{YZ}}
{\sqrt{(1-r_{XZ}^2)(1-r_{YZ}^2)}}
ここで
- $(u_x):(X) を (Z)$に(切片ありで)回帰したときの残差
- $(u_y):(Y) を (Z) $に(切片ありで)回帰したときの残差
1.6. 2変数データの記述と要約
回帰直線
説明変数 $(x)$、目的変数 $(y)$ に対して、単回帰モデルを考える:
y_i = \beta_0 + \beta_1 x_i + \varepsilon_i \quad (i=1,2,\dots,n)
ここで
- $\beta_0:切片$
- $\beta_1:回帰係数$
- $\varepsilon_i:誤差項$(残差$e_i$の理論的な値$\varepsilon_i$⇔$e_i$は$\varepsilon_i$の推定値)
残差平方和は
S(\beta_0, \beta_1) = \sum_{i=1}^n \left( y_i - \beta_0 - \beta_1 x_i \right)^2
この式を$\beta_0, \beta_1$ で偏微分して0となる極小値条件は
\frac{\partial S}{\partial \beta_0} = -2 \sum_{i=1}^n \left( y_i - \beta_0 - \beta_1 x_i \right) = 0
\frac{\partial S}{\partial \beta_1} = -2 \sum_{i=1}^n x_i \left( y_i - \beta_0 - \beta_1 x_i \right) = 0
整理すると次の連立方程式(正規方程式)
\sum_{i=1}^n y_i = n \beta_0 + \beta_1 \sum_{i=1}^n x_i
\sum_{i=1}^n x_i y_i = \beta_0 \sum_{i=1}^n x_i + \beta_1 \sum_{i=1}^n x_i^2
平均を $\bar{x}, \bar{y}$ とすると、解は
\hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}
{\sum_{i=1}^n (x_i - \bar{x})^2}
= \frac{\mathrm{cov}(x,y)}{\mathrm{var}(x)}
\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}
したがって、最小二乗法による回帰直線は
\hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_i
これらの式から、次の考察が得られる。
- 予測値の平均と観測値の平均は等しい。
\frac{1}{n}\sum_{i=1}^n y_i = \frac{1}{n}・n \beta_0 + \frac{1}{n}\beta_1 \sum_{i=1}^n x_i
\bar{y} = \beta_0 + \beta_1 \bar{x}=\bar{\hat{y}}
- 残差$e_i=y_i-\hat{y_i}$の平均は0となる
\bar{e}=\bar{y}-\bar{\hat{y}}=0
- 回帰直線は$(\bar{x},\bar{y})$を通る
- 予測値$\hat{y}_i$と残差$e_i$の相関係数は0
- 決定係数$R^2$は次の式で示される
R^2=\frac{S_R}{S_y}=\frac{\sum (\hat{y_i}-\bar{y})^2}{\sum (y_i-\bar{y})^2}
質的データのクロス集計表
下図のような表を2元クロス集計表という。
| 大きさ\家賃 | 安い | 高い | 計 |
|---|---|---|---|
| 狭い | 57 | 8 | 65 |
| 広い | 22 | 53 | 75 |
| 計 | 79 | 61 | 140 |
上記表をパーセンテージ表記にすると以下の通り
| 大きさ\家賃 | 安い | 高い | 計 |
|---|---|---|---|
| 狭い | 87.7 | 12.3 | 100 |
| 広い | 29.3 | 70.7 | 100 |
ここで、部屋が「狭い」ことにより家賃が「安く」なることが、広い場合に対してどのくらいか(オッズ比)計算する。
Odds.ratio=\frac{\frac{0.877}{0.123}}{\frac{0.293}{0.707}}=\frac{7.130}{0.414}=17.2倍
1.7 時系列データの記述と簡単な分析
幾何平均
幾何平均は時系列データに適用するのが良い。例えば、幾何平均で求めた年平均変化率であれば、考慮する期間の累乗は正確に定量的な数値を返す。算術平均では正しい値より大きい値が出る。
(\sum_{t=1}^T r_t)^{1/T} = \sqrt[T]{r_1*r_2*…*r_{T-1}*r_T}
時系列データの変動分解
時系列データは以下の3つに分解されることがある。
- 傾向変動$(TC)$: 循環する場合も含めた長期変動
- 季節変動$(S)$: 1年周期の循環変動
- 不規則変動$(I)$: 上記の変動に含まれない
y_t = TC_t+S_t+I_t
傾向変動TCを抽出できる移動平均法
ある時点$t$の傾向変動$TC_t$とすると、時点$t$前後の$k$個のデータ$(y_{t-k},…,y_t,…,y_{t+k})$を用いて、
\hat{TC_t} = \sum_{t=t-k}^{t+k}\frac{y_s}{2k+1}
とする。時点$t$を動かしながら平均をとるため、$\hat{TC_t}$を移動平均という。周期$2k+1$の季節変動は除去される。なお、年間12か月の移動平均など偶数(≠2k+1)となる際は、k=5.5として最初と最後の項(t-6,t+6項)の半分の値を加えて、次のように計算する
\hat{TC_t} = \frac{\frac{y_{t-6}}{2}+y_{t-5}+…+y_{t+5}+\frac{y_{t+6}}{2}}{12}
この式から傾向変動を求めると、平均が0ではない$y_t-TC_t$を平均0に標準化すると、季節変動$S$が計算できる。
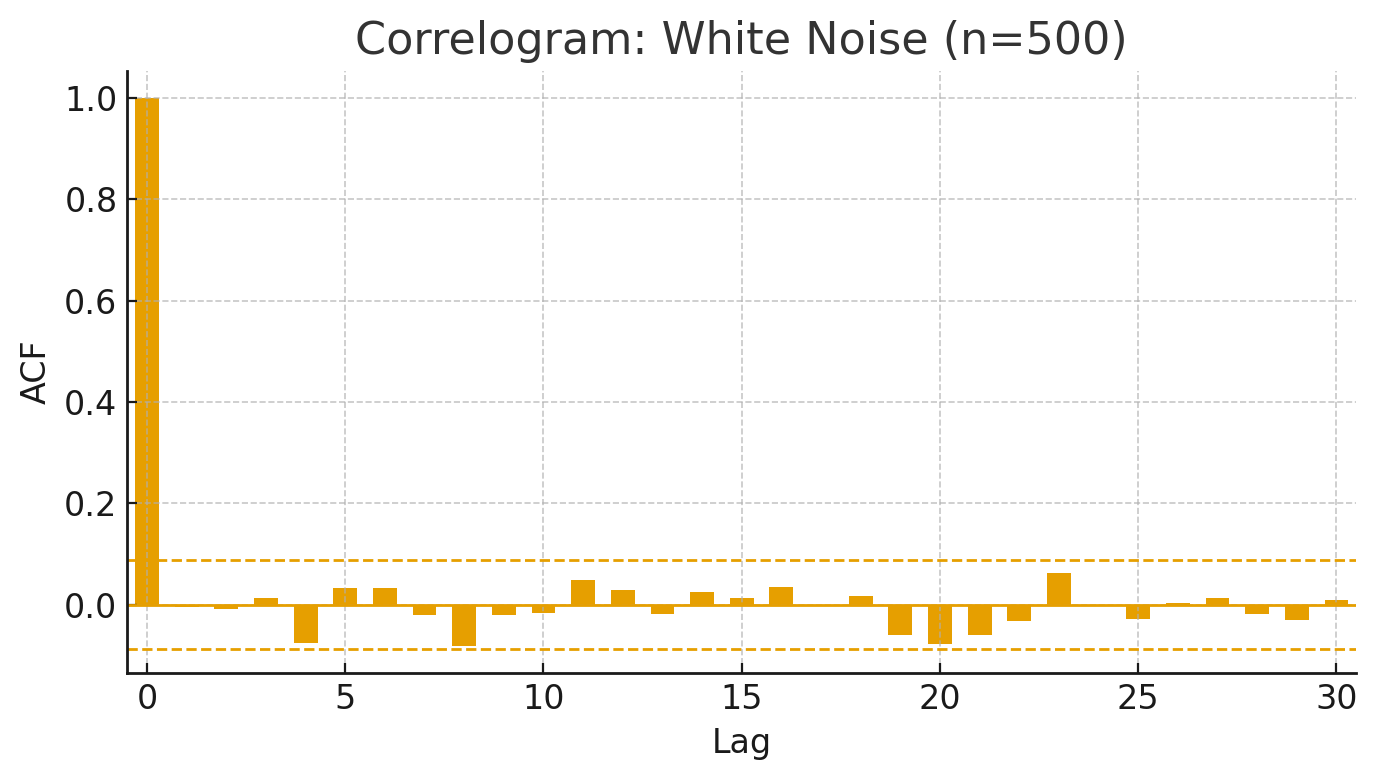
自己相関係数
時系列データにおいて、自身のデータ群から時点hだけずらしたデータ群との相関係数を自己相関係数と呼ぶ。
ここで$h$をラグと呼ぶ。自己相関係数を求めるために自己共分散関数を
C_h = \frac{1}{T}\sum_{t=1}^{T-h}(y_t-\bar{y})(y_{t+h}-\bar{y}), h=0,1,2,…
で計算し、それを用いて自己相関係数は
r_h = \frac{C_h}{C_0}
縦軸を$t_h$、横軸をラグ$h$としたグラフをコレログラムと呼ぶ。コレログラムは「この時系列がどれくらい 過去と似ているか を、時間差ごとに可視化したもの」。
各種指数
- ラスパイレス指数
ラスパイレス指数は基準年の買い物かごをそのままにして「今の価格で買うといくらかかるか」を計算し、基準年の支出と比べるイメージ。式は
\frac{\sum_{i}p_{ti}q_{0i}}{\sum_{i}w_i}
分母は基準年の買い物かご全体の価格、分子は品目の数は変えず$(q_{0i})$に新しい価格$p_{ti}$を掛けて、価格比較をする。ほかにもパーシェ式とフィッシャー式がある。
ラスパイレス指数と実質GDPの関係
- 実質GDP(基準年価格表示)
GDP^{\text{real}}_t = \sum_i q_{i,t} \, p_{i,0}
- ラスパイレス数量指数
Q^L_t = \frac{\sum_i q_{i,t}\, p_{i,0}}{\sum_i q_{i,0}\, p_{i,0}}
実質GDPをラスパイレス数量指数で書き直すと
GDP^{\text{real}}_t
= Q^L_t \times \sum_i q_{i,0}\, p_{i,0}
= Q^L_t \times GDP^{\text{nominal}}_0
つまり、実質GDPはラスパイレス数量指数と基準年の名目GDPの積である。
- ラスパイレス数量指数は比率(無次元の指数)
- 実質GDPは金額(基準年価格で測ったGDP)
- 両者の関係は
GDP^{\text{real}}_t = Q^L_t \times GDP^{\text{nominal}}_0
したがって「ラスパイレス数量指数=実質GDP」と言うときは、厳密には比例関係にあるという意味となる。