【Atcoder解法検討】ABC131 A~D Python

A - Security

問題ページ : A - Security

考察

標準入力、条件分岐による出力。
4桁と小さいためループなど回さず判定条件3つを列記しました。

コード

S = input()
print("Bad" if S[0] == S[1] or S[1] == S[2] or S[2] == S[3] else "Good")

B - Bite Eating

問題ページ : B - Bite Eating

考察

　リンゴ1とリンゴNの味だけから高速に解く方法もありそうですが、全探索しても十分に間に合いそうです。全探索できるなら全探索した方がミスは発生しにくいと思います。
　今回はリンゴの味の絶対値が最低のものを全探索でみつけてN個全てのリンゴの味から引くという方法でコードを組みました。

コード

N, L = map(int, input().split())
A = [L + i - 1 for i in range(1,N+1)]
total = sum(A)
dmin = float("inf")
ans = 0
for a in A:
    if abs(a) < dmin:
        ans = total - a
        dmin = abs(a)
print(ans)

C - Anti-Division

問題ページ : C - Anti-Division

考察

　まずA以上B以下の範囲の全探索はTLEとなるでしょう。次に、それぞれA以上B以下で
$$CでもDでも割り切れない個数 = 全個数 - CまたはDで割り切れる個数$$
となります。また
$$CまたはDで割り切れる個数 = Cで割り切れる個数 + Dで割り切れる個数 - CでもDでも割り切れる個数$$
であり、
$$CでもDでも割り切れる個数 = C,Dの最小公倍数で割り切れる個数$$
です。
よって最小公倍数の求め方とA以上B以下でxで割り切れる数字の個数の数え方があれば本問題の解答を作成することができます。
前者、最小公倍数については
$$x,yの最小公倍数\ =\ x \times\ y\ /\ x,yの最小公約数$$
で最小公約数はユークリッド互除法で計算できます。
また、後者については
$$ A以上B以下でxで割り切れる数字個数 = B\ //\ x\ -\ (A-1)\ //\ x$$
で求められます。Aがxで割り切れるかで否かで場合分けが必要にならないよう、右辺第二項を$(A-1)\ //\ x$としています。

コード

A, B, C, D = map(int, input().split())

#最大公約数
def gcd(a,b):
  if b == 0: return a
  return gcd(b, a % b)

# A以上Ｂ以下でxで割り切れる数
def cal(x):
  global A, B
  large = B // x
  small = (A-1) // x
  return large - small

# E:C,Dの最小公倍数
E = C * D // gcd(C, D)

# CまたはDで割り切れる個数
tmp = cal(C)+cal(D)-cal(E)

# CでもDでも割り切れない個数
print(B - A + 1 -tmp)

D - Megalomania

問題ページ : D - Megalomania

考察

貪欲法で〆切時間の早い仕事から実施し各仕事が各〆切時間内に終了するか確認、という方法で正解が得られます。

コード

N = int(input())
JOB = []
for _ in range(N):
    JOB.append(tuple(map(int, input().split())))

#JOBを各tupleの第2項でソート
JOB.sort(key = lambda x:x[1])

ans = "Yes"
totaltime = 0
for A,B in JOB:
    totaltime += A
    if totaltime > B:
        ans = "No"
        break

print(ans)

E - Friendships

問題ページ : E - Friendships

考察

　まず単純なグラフの意味するところですが、これは自己ループと多重辺が無いということです。ここはしっかりと認識する必要があります。
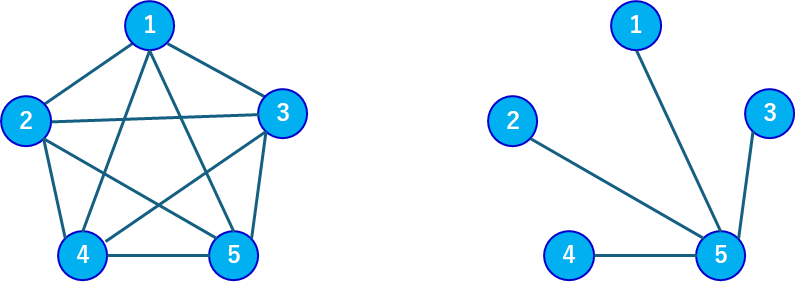
　次に条件をみたすグラフが存在しないこともあるとのことですので、グラフが存在するためのKの範囲を考えます。Kの下限は下図左側のような完全グラフで0となります。すべて二頂点の距離が1となるからです。
　一方で上限は下図右側のような一つの頂点を根として他の全ての頂点が直接つながっている木です（構造的にはスター型）。これは根を含まない全ての二頂点組み合わせが距離2となり、その個数は$\frac{(N-1)(N-2)}{2}$となります。

　なおこの値が最大値である理論的根拠としては、全ての頂点の組み合わせは$\frac{N(N-1)}{2}$ですが、グラフは連結であるため$N-1$個の組み合わせは二頂点が距離1でつながっています。
$$\frac{N(N-1)}{2} \ - (N-1) \ = \frac{(N-1)(N-2)}{2}$$
よって最大値となることが確認されました。
　そしてこの最大値構造から根を含まない二頂点を直接つないでいくとその二頂点間は距離2から1となり、距離2となる二頂点の組み合わせをひとつずつ減らしていけます。

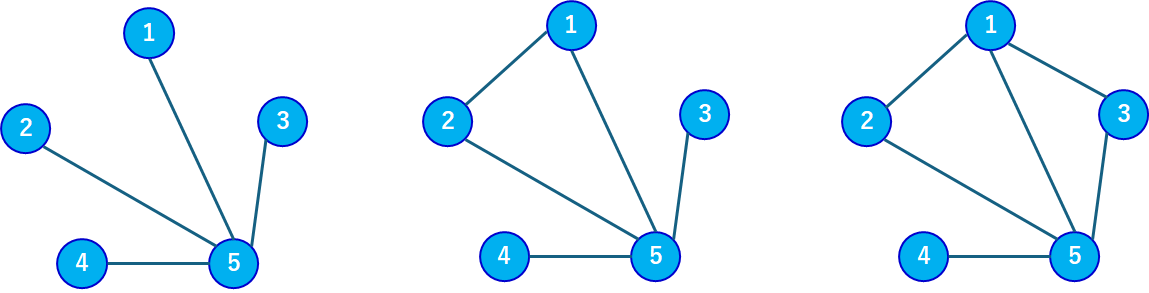
　上記内容をほぼそのままコードに反映させるとACに到ります。

コード

N, K = map(int, input().split())

cmax = (N-1) * (N-2) // 2
cnum = cmax - K

# 上限超えた場合-1を表示して終了
if K > cmax:
    print(-1)
    exit()

# Nを中心とするスター型を作成
ans = []
for i in range(1,N):
    ans.append((i,N))

# 1本づつパス１でつないで数を合わせる
cnt = 0
for i in range(1,N):
    for j in range(i+1,N):
        if cnt >= cnum:break
        ans.append((i,j))
        cnt += 1

# 解出力
print(len(ans))
for u,v in ans:
    print(u,v)

F -

問題ページ : F -

青色diff以上は後日挑戦