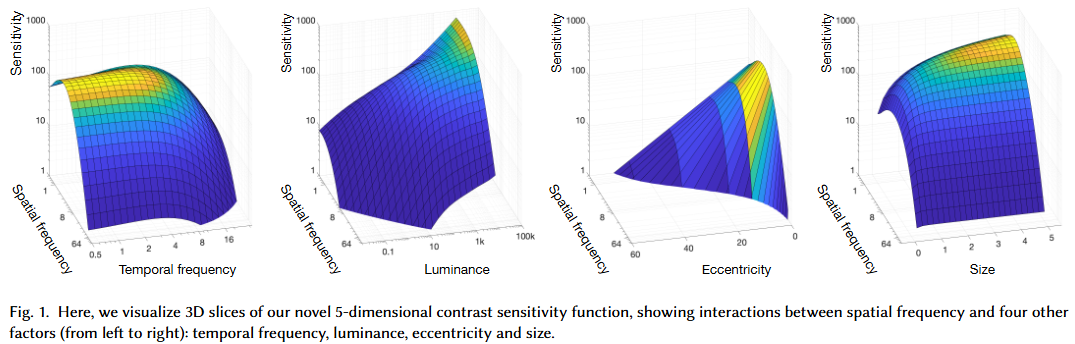
stelaCSF - A Unified Model of Contrast Sensitivity as the Function of Spatio-Temporal Frequency, Eccentricity, Luminance and Area (2022)

Posted at 2025-10-15

stelaCSF - A Unified Model of Contrast Sensitivity as the Function of Spatio-Temporal Frequency, Eccentricity, Luminance and Area (RAFAŁ K. MANTIUK, 2022)

3行要約

従来のContrast Sensitivity Function (CSF) は、空間周波数や輝度など刺激の主要な次元の一部しか扱えず、適用範囲が限定されるという課題がありました。
本研究は、空間・時間周波数、輝度、離心率、面積という5つの主要な刺激次元すべてを統合的に説明する新しいCSFモデル「stelaCSF」を提案し、複数のデータセットを単一のパラメータセットで高精度に予測します。
stelaCSFは、低周波数を含む全ドメインで既存モデルを大幅に上回る精度を示し、フリッカー検出やFoveated Renderingといったコンピュータグラフィックスの分野での実用性を実証しました。

Q:何が問題で、それをどのように解決したのか、わかりやすく説明してください

A:

🚀 問題：人間の「見えやすさ」を予測するのが難しかった！

私たちがディスプレイを見たり、現実世界を見たりするとき、何が「見えやすい」のか、何が「見えにくい」のかは、たくさんの要因で変わってきます。例えば：

物の細かさ（空間周波数）: すごく細かい模様は、遠くからだと見えにくいですよね。
物の動きの速さ（時間周波数）: チラつきが速すぎると、動きが認識できなくなります。
周りの明るさ（輝度）: 暗い場所では、細かいものが見えにくいです。
見ている場所（偏心）: 視線の中心（真ん中）はよく見えますが、端っこ（周辺視野）はぼんやりします。
物の大きさ（面積）: 小さすぎるものは、たとえ真ん中にあっても見えにくいことがあります。

これら5つの要因は、それぞれがバラバラに「見えやすさ」に影響するだけでなく、互いに複雑に影響し合います。

従来のモデルの問題点:

これまでの研究でも、この「見えやすさ」を予測するモデル（Contrast Sensitivity Function: CSF）はたくさんありました。しかし、そのほとんどは、上記の要因のうち一部しか考慮していなかったのです。

例えば、「静止画」は予測できるけど、「動きのある動画」は予測できない。
「視線の中心」では予測できるけど、「周辺視野」では予測できない。
「普通の明るさ」では予測できるけど、「すごく暗い場所」や「すごく明るい場所」では予測できない。

つまり、現実世界や現代のVR/ARディスプレイのように、これらの要因が同時に、かつ広範囲にわたって変化するような状況では、従来のモデルでは「正確に何が見えるか」を予測するのが非常に難しかったのです。これは、新しいディスプレイ技術やグラフィック技術を開発する上で大きな課題でした。

✨ 解決策：5つの要因をまとめて予測できる「統一モデル」を開発！

stelaCSFは、この「5つの要因が絡み合う複雑な状況での見えやすさ予測」という問題に挑戦しました。

stelaCSFの解決策のポイント:

5つの要因をすべて考慮:
stelaCSFは、空間周波数、時間周波数、輝度、偏心、面積という5つの主要な要因すべてを、単一のモデルで同時に考慮できるようにしました。これにより、「動きのある、周辺視野にある、暗い場所の、特定の大きさの細かい模様」がどのくらい見えやすいか、といった複雑な状況も一度に予測できます。
過去の膨大なデータを統合:
この5つの要因をすべて同時に測定する実験は、あまりにも時間がかかりすぎて現実的ではありません。そこでstelaCSFは、過去に発表された11もの異なる研究から集めた膨大なデータを、賢く組み合わせて利用しました。それぞれの研究は、5つのうち特定の要因の組み合わせに焦点を当てていましたが、それらを合わせることで、5次元空間全体の情報をカバーできるようにしたのです。
視覚科学の知見を組み込んだ数式:
ただデータを集めて数字を合わせるだけでなく、人間の目がどのように機能するかという視覚科学のこれまでの知見（心理物理学的モデル）に基づいて数式を構築しました。これにより、なぜそのように感度が変化するのかを説明できる、より信頼性の高いモデルができました。
単一のパラメータセットで汎用性高く:
従来のモデルがデータセットごとにパラメータを調整し直す必要があったのに対し、stelaCSFはたった一つのパラメータセットで、11もの異なるデータセットすべてを高い精度で予測できるように設計されています。これにより、どんな状況でも、一度モデルを組み込めば、再調整なしで使えるという大きなメリットが生まれました。

この解決策によって何ができるようになったか:

stelaCSFを使えば、例えば以下のようなことが、より正確に、かつ効率的にできるようになります。

VR/ARでの画面の最適化（中心窩レンダリング）: ユーザーが見ている中心部分は高画質に、あまり見ていない周辺部分は画質を落としても、人が気づかないようにできます。ディスプレイの解像度や明るさに合わせて、自動で最適な設定を見つけ出せます。
動画のチラつき（フリッカー）の検出: 動画のどこで、どんな明るさや動きの速さのときに、人がチラつきを感じやすいかを正確に予測し、対策を講じることができます。
画像・動画圧縮: 人が見えにくい部分の情報を大胆に削減しても、画質が劣化していると感じさせない圧縮技術を開発できます。

簡単に言えば、stelaCSFは、これまでバラバラにしか予測できなかった「人間の見えやすさ」を、**「どんな状況でもまとめて予測できる、賢い計算式」**として提供した、というわけです。

Q:そもそもContrast Sensitivity Function (CSF) とは何ですか？

A:

Contrast Sensitivity Function (CSF) について、とても良い質問ですね。これは人間の視覚を理解する上で非常に基礎的かつ重要な概念です。

Contrast Sensitivity Function (CSF) とは

Contrast Sensitivity Function (CSF) は、日本語で「コントラスト感度関数」と訳されます。これは、人間の視覚システムが、さまざまな空間周波数や時間周波数を持つコントラストパターンをどの程度検出しやすいかを示す関数です。

もう少し具体的に見ていきましょう。

コントラスト (Contrast):
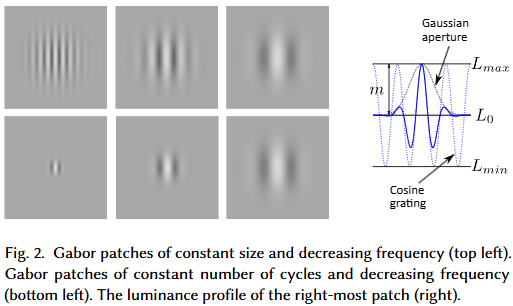
まず、「コントラスト」とは、画像の明るい部分と暗い部分の差の度合いを指します。stelaCSFの論文でも説明されている「Michelson contrast」$c$は、以下の式で定義されます。
$$
c = \frac{L_{max} - L_{min}}{L_{max} + L_{min}}
$$
ここで、$L_{max}$は刺激の最大輝度、$L_{min}$は最小輝度です。コントラストが高いほど、画像ははっきりとして見えやすくなります。
感度 (Sensitivity):
「感度」とは、ある刺激を知覚するために必要なコントラストの逆数です。
$$
S = \frac{1}{c_{threshold}}
$$
ここで、$c_{threshold}$は「閾値コントラスト」と呼ばれ、そのパターンをかろうじて検出できる最小のコントラストを意味します。
感度が高いほど、人間はより小さなコントラストの違いでもパターンを知覚できる、つまり「見えやすい」ということです。
関数 (Function):
CSFが「関数」である理由は、この感度が様々な刺激パラメータによって変化するからです。主要なパラメータは以下の通りです。
- 空間周波数 ($\rho$):
  これは、画像の細かさ（ディテール）を表します。単位は cpd (cycles per degree: 視覚角度1度あたりのサイクルの数) で表されます。
  - 低い空間周波数: 粗いパターン（例: 大きなぼやけた縞模様）。
  - 高い空間周波数: 細かいパターン（例: 細かい縞模様）。
    一般的に、人間は中程度の空間周波数（数cpd〜十数cpd）で最も感度が高く、低すぎても高すぎても感度が低下します。
- 時間周波数 ($\omega$):
  これは、刺激の時間的な変化の速さを表します。単位は Hz (ヘルツ) です。
  - 低い時間周波数: ゆっくりとした変化（例: ゆっくりと明滅する光）。
  - 高い時間周波数: 速い変化（例: 高速で明滅する光、フリッカー）。
    一般的に、静止画（0 Hz）でもコントラストを見ることができますが、ある程度の速さで変化するパターン（数Hz〜十数Hz）で最も感度が高く、それ以上速くなるとフリッカーとして知覚されなくなり、感度が急激に低下します。
stelaCSFがさらに拡張したのは、この空間周波数と時間周波数だけでなく、以下のパラメータも感度を決定する重要な要素として組み込んだ点です。
- 輝度 ($L$): 背景の明るさ。
- 偏心 ($e$): 視野の中心（中心窩）からの距離。
- 面積 ($a$): 刺激のサイズ。

CSFがなぜ重要なのか

CSFは、人間の視覚システムがどのように機能するかを理解するための「足がかり」となります。

視覚システムの応答特性: CSFは、人間の目が特定の空間的・時間的情報に対してどの程度「チューニング」されているかを示します。例えば、人間の目は細かい動き（高空間周波数＋低時間周波数）よりも、中程度の速さで変化するパターン（中空間周波数＋中時間周波数）に敏感であることがCSFから分かります。
画像・動画品質評価: 画像や動画の品質を評価する際、CSFは「何が見えるか、何が見えないか」の基本的な基準となります。例えば、圧縮アルゴリズムで失われた情報がCSFの感度の低い領域にあれば、その劣化は知覚されにくいと予測できます。
ディスプレイ技術: ディスプレイの解像度、リフレッシュレート、輝度などの設計において、CSFはユーザー体験を最適化するためのガイドラインとなります。stelaCSFの「中心窩レンダリング」の例が良い例ですね。
医療診断: 眼疾患の診断や視機能検査にも用いられます。
コンピュータグラフィックス: レンダリング手法やアーティファクトの可視性予測など、さまざまな応用があります。

典型的なCSFの形状

CSFをプロットすると、多くの場合、空間周波数に対して逆U字型（バンドパスフィルターのよう）の形状を示します。つまり、中程度の空間周波数で感度がピークに達し、低空間周波数（非常に大きなぼやけたパターン）と高空間周波数（非常に細かいパターン）の両方で感度が低下します。時間周波数を考慮すると、さらに複雑な3Dの「表面」を描くことになります。

stelaCSFは、このCSFをさらに5次元に拡張し、より広範な視覚条件下での人間の感度を統一的に予測できるモデルとして提案されたもの、ということになります。

Q:この論文の概要を教えてください

A:

本論文は、空間周波数、時間周波数、輝度、視覚野における位置（eccentricity）、刺激の面積（area）という5つの主要な次元を統一的に扱う新しいコントラスト感度関数（CSF: Contrast Sensitivity Function）モデル stelaCSF を提案しています。従来のCSFモデルはこれらの次元の一部しか考慮しておらず、用途が静的または中心窩のコンテンツに限定されるという課題がありました。また、高次元のコントラスト感度空間を単一の実験で測定することは困難であり、これまでのモデルは個別のデータセットに特化してフィッティングされていました。

stelaCSF の主な貢献は以下の点にあります。

統合データセットの構築と公開: 11の既存研究から得られたコントラスト感度データを統合・標準化し、大規模なデータセットとして公開しています。これにより、モデルの広範な検証とフィッティングが可能となりました。
既存モデルの定量的分析: 既存のCSFモデルが測定データをどの程度予測できるかについて、定量的な分析を実施し、その限界を明らかにしています。
新しい統一CSFモデル stelaCSF の提案: 上記5次元すべてを考慮し、既存のモデルを大幅に上回る予測精度を持つ stelaCSF を導入しています。モデルのソースコードも公開されています。
応用例の実証: stelaCSF の実用性をフリッカー検出メトリックとFoveated Renderingの改善に応用することで示しています。

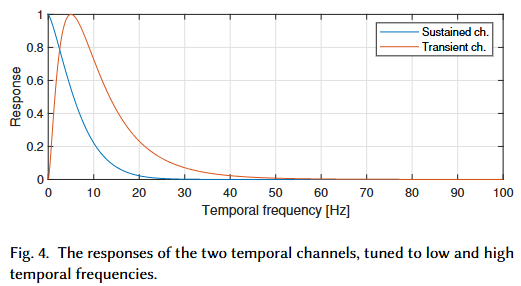
stelaCSF の中核となる手法は、以下のコンポーネントを組み合わせた心理物理学的モデルに基づいています。モデルは、持続（sustained, S）と過渡（transient, T）の2つの時間チャネルが独立して視覚情報を処理するという前提に立っています。最終的なコントラスト感度 $S$ は、各時間チャネルの応答の合計として以下のように定義されます。

$$S (\rho, \omega, L, a, e) = S_{ecc} (e, \rho) [R_S (\omega) S_{A,S} (\rho, a, L) + R_T (\omega) S_{A,T} (\rho, a, L)]$$

ここで、各要素は以下のようにモデル化されます。

サイズと空間周波数 ($S_A$):
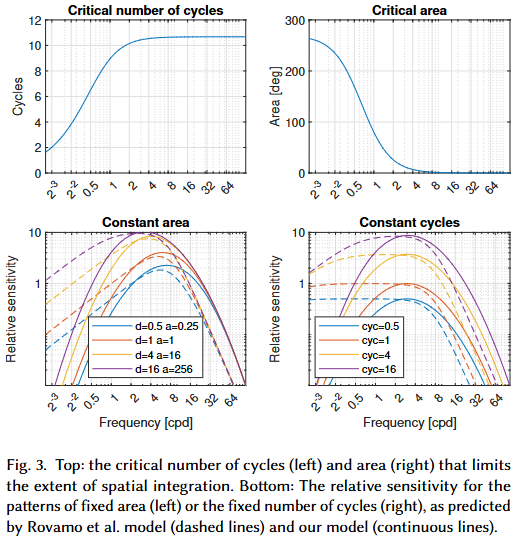
Rovamoらの研究に基づき、刺激の面積 $a$ と空間周波数 $\rho$ に依存する感度 $S_A$ をモデル化しています。特に、低空間周波数での感度低下と高空間周波数での光学系による感度低下を考慮するため、修正された Truncated log-parabola を使用しています。
$$S_A (\rho, a, L) = S_m (L) \frac{a_c}{1 + a_c/a} \rho S_{LP} (\rho)$$
$S_m (L)$ は輝度依存のピーク感度、$a_c$ は臨界面積、そして $S_{LP} (\rho)$ は以下のように定義されます。
$$S_{LP} (\rho) = \begin{cases} 1 - k_a & \text{if } \rho < \rho_m \text{ and } S_{LP} < 1 - k_a \ 10^{- \frac{(\log_{10} \rho - \log_{10} \rho_m (L))^2}{2k_b}} & \text{otherwise} \end{cases}$$
ここで、$\rho_m (L)$ は輝度依存のピーク周波数を制御し、$k_a$ は低周波での感度低下を制限し、$k_b$ はバンド幅を制御するパラメータです。
時間周波数 ($R_S, R_T$):
持続（S）と過渡（T）の2つの時間チャネルの応答をモデル化するために、一般化指数関数を使用しています。
$$R_S (\omega) = \exp \left( - \frac{\omega^{\beta_S}}{\sigma_S} \right)$$
$$R_T (\omega) = \exp \left( - \frac{\omega^{\beta_T} - \omega^{\beta_{T0}}}{\sigma_T} \right)$$
ここで、$\omega$ は時間周波数であり、$\beta_S, \sigma_S, \beta_T, \sigma_T, \beta_{T0}$ はモデルのパラメータです。
輝度 ($S_m, \rho_m$):
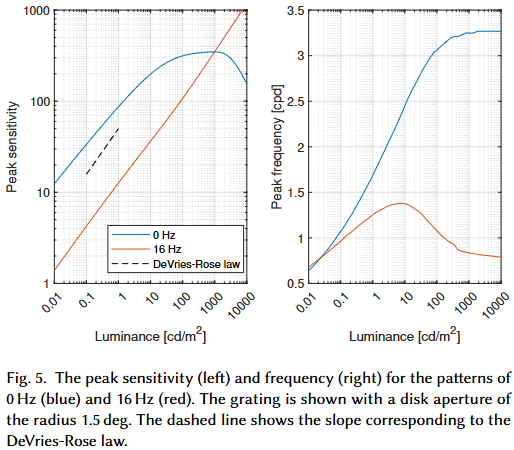
輝度 $L$ が感度のピーク値 $S_m$ とピーク周波数 $\rho_m$ に与える影響を、持続チャネルと過渡チャネルで別々にモデル化しています。持続チャネルは DeVries-Roseの法則からWeberの法則への移行と高輝度での感度低下を示し、過渡チャネルはDeVries-Roseの法則に従うと仮定しています。
$$S_{m,S} (L) = k_{s1,S} \frac{1 + k_{s2,S}L^{-k_{s3,S}}}{1 - (1 + k_{s4,S}L^{-k_{s5,S}})}$$
$$S_{m,T} (L) = k_{s2,T} L^{k_{s1,T}}$$
ピーク周波数シフトについては、
$$\rho_{m,S} (L) = k_{\rho1,S} \frac{1}{1 + k_{\rho2,S}L^{-k_{\rho3,S}}}$$
$$\rho_{m,T} (L) = k_{\rho,T}$$
ここで $k_{\dots}$ はモデルのパラメータです。
視覚野における位置 ($S_{ecc}$):
視覚野における位置（eccentricity, $e$）による感度低下は、対数感度、eccentricity、および空間周波数の線形関係に基づいてモデル化されています。これにより、中心窩から離れるにつれて感度が低下する現象を捉えます。また、周辺視の異方性（鼻側とその他の方向で感度低下が異なること）を考慮するため、異なるパラメータセットを導入し、補間を行っています。
$$S_{ecc} (e, \rho) = 10^{\hat{k}_{e1}\rho e + \hat{k}_{e2}e}$$
$\hat{k}_{e1}, \hat{k}_{e2}$ は視覚野の方向に応じて補間されるパラメータです。

モデルのフィッティングと検証には、ModelFest、HDR-VDP、HDR-CSFなど、広範な条件で測定された11のデータセットが用いられました。stelaCSF は、3次元、4次元、5次元すべての比較において、既存のBartenのCSF、VDP CSF、RovamoらのCSF、FovVideoVDPのCSF（fvvdpCSF）と比較して、最も低い予測誤差（RMSE）を達成しました。特に、fvvdpCSFと比較して統計的に有意な改善が見られました。

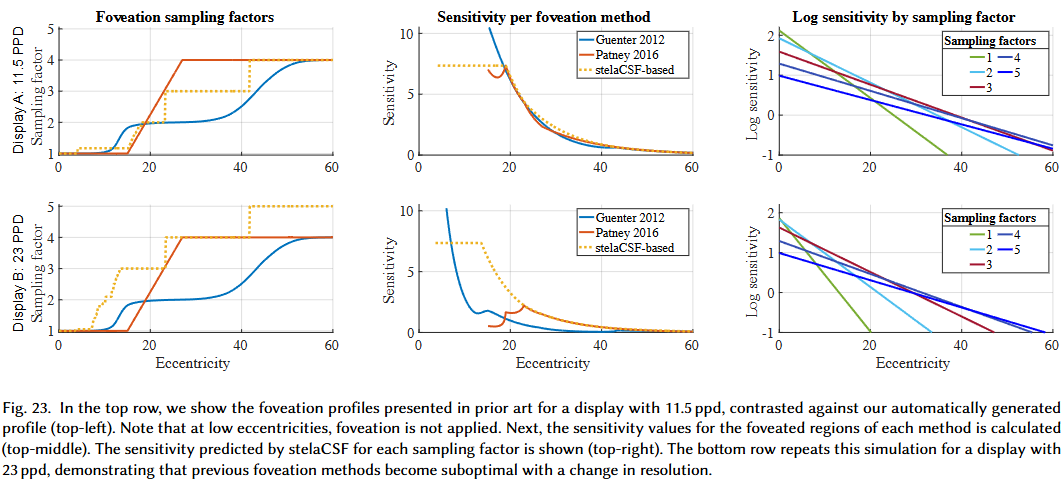
応用例として、まずコントラストエネルギーモデルとの組み合わせにより、複雑なパターンに対する視認閾値を予測できることを示しました。次に、DenesとMantiukのフリッカー検出アルゴリズムに stelaCSF を組み込むことで、Krajancichらの研究で検証されたような、視覚野における位置依存のフリッカー検出をより正確に行えることを示しました。最後に、Foveated Renderingにおいて、ディスプレイ解像度などのパラメータ変化に応じて知覚的に最適なサンプリングプロファイルを自動生成できることを実証し、手動で設計されたプロファイルが異なるディスプレイ条件で非最適になる可能性を指摘しています。

本モデルは、高時間周波数領域でのCFF（Critical Flicker Fusion frequency）測定値の予測精度や、輝度とeccentricity間の相互作用のモデリング、および色コントラスト感度への拡張が今後の課題として挙げられています。

Q:関連手法との比較について詳しく説明してください

A:

人間の視覚系のコントラスト感度機能（CSF）は、視覚モデルの基礎となる重要な要素ですが、既存のCSFモデルは、刺激を記述する多くの関連する次元（空間周波数、時間周波数、輝度、偏心、面積など）のうち、一部しか考慮していないことが一般的でした。そのため、従来のモデルは、静的な中心窩のコンテンツに限定されるか、移動する中心窩のコンテンツに限定されるなど、使用範囲が制限されていました。

stelaCSFは、これらすべての主要な次元を統一的にモデル化することで、この課題に対処しようとしています。

主要な関連CSFモデルと`stelaCSF`との比較

論文では、既存のCSFモデルを以下のように分類し、stelaCSFの優位性を説明しています。

空間周波数、サイズ、輝度、偏心に対応するモデル (3〜4次元)
- Rovamoとその同僚のモデル (Rovamo et al. 1993, Mustonen et al. 1993, Rovamo et al. 1995, Virsu and Rovamo 1979):
  - 特徴: 刺激のサイズ、輝度レベル、偏心にわたる感度を支配する単純な関係を提案しました。stelaCSFは、彼らのデータとアイデアをベースラインモデルとして利用しています。
  - 課題: 定数サイクル（constant-cycle）のGaborパッチに対して、低周波数での感度低下を予測できないこと（図3下右）や、中心窩外での高周波数での感度低下を説明できないことといった弱点がありました。
- DalyのVDP CSF (Daly 1992):
  - 特徴: 最も完全なコントラスト感度モデルの一つとして知られていますが、その作成に関する詳細は少ないです。
  - stelaCSFとの比較: 表3のRMSE比較では、stelaCSFの方がVDP CSFよりも低いエラー値を示しています。
- Bartenのモデル (Barten 1999, 2003):
  - 特徴: 視覚系に見られるノイズや減衰源を原理的にモデル化し、SMPTE 2084やITU-R 2100といった様々なアプリケーションや標準で広く採用されています。光視（photopic）だけでなく、薄明視（mesopic）や暗視（scotopic）のデータも予測できるとされています。
  - 課題: 偏心（eccentricity）を考慮していません。
  - stelaCSFとの比較: 表3のRMSE比較では、BartenのCSFはそのスコープ内では良い性能を示しますが、stelaCSFはより多くの次元を統合し、全体的な予測精度で優れています。
- Yi et al. (2022) のモデル:
  - 特徴: 周囲の輝度へのコントラスト感度の依存性を追加しています。stelaCSFは、この周囲の輝度の効果をグレアや局所適応として別途モデル化できると考えています。
時間周波数を考慮するモデル (主に2次元)
- Kelly-Dalyのモデル (Kelly 1979b, Daly 1998):
  - 特徴: spatio-temporalパターンを体系的に研究し、spatio-temporal CSFを提案しました。Kellyの研究は眼球運動を補償した刺激で測定されており、感度が高周波数側に強くシフトしていました。
  - 課題: 他の次元（輝度、偏心、サイズなど）を考慮していません。
  - stelaCSFとの比較: stelaCSFはKelly-Dalyのモデルも組み合わせていますが、その単体では多次元のCSFを構築できません。stelaCSFは、Kellyのデータが眼球運動補償のため他のデータセットと異なりすぎると判断し、直接的な比較対象から外しています。
簡略化された多次元モデル (3〜4次元、ただし制限あり)
- WatsonとAhumadaのPyramid of Visibility (PoV) (Watson and Ahumada 2016, Watson 2018):
  - 特徴: コントラスト感度の対数を、空間・時間周波数および網膜照度の対数の線形モデルとしてうまく説明できると提唱しました。そのシンプルさから魅力的です。後にWatson (2018) によって偏心効果も考慮されるようになりました。
  - 課題: 10 cpd以下、10 Hz以下の周波数をモデル化できないという大きな制限があります。これは、VRヘッドセットが再現できる周波数帯域など、視覚コンテンツの基本的な部分と重なるため、実用上の大きな制約となります。また、刺激サイズの影響を考慮していません。
  - stelaCSFとの比較: stelaCSFは、PoVが刺激サイズの影響を考慮せず、低周波数で有効な予測を提供できないため、表3のRMSE比較には含めていません。図7では、PoVが低spatio-temporal周波数で頂点を持たないのに対し、stelaCSFはより複雑な形状の可視性の境界をモデル化できることを示しています。
- Ahumada et al. (2018) のデュアルチャンネルモデル:
  - 特徴: 視覚系におけるパルボ細胞経路とマグノ細胞経路の存在に動機づけられ、2つの時間チャンネルを使ってspatio-temporal感度をモデル化することを提案しました。
  - stelaCSFとの関連: stelaCSFも、同様に低時間周波数と高時間周波数に対応する2つの時間チャンネル（持続チャンネルと過渡チャンネル）を採用し、時間感度をモデル化しています。
stelaCSFと同じ5次元を考慮する既存モデル
- FovVideoVDPのCSF (fvvdpCSF) (Mantiuk et al. 2021):
  - 特徴: stelaCSFが認識している中で、唯一同じ5次元を考慮するモデルです。spatio-chromatic CSF (Mantiuk et al. 2020)、皮質拡大モデル、Kelly-Dalyのモデルの組み合わせに基づいています。
  - 課題: 低空間周波数と高空間周波数の両方で大きな予測誤差が生じることが示されています（セクション6.2）。皮質拡大モデルが一部のデータセットと矛盾する結果を示すことも指摘されています。
  - stelaCSFとの比較: stelaCSFは、このfvvdpCSFを直接の競合モデルとして詳細に比較しています。表3のRMSE比較では、stelaCSFがfvvdpCSFを大幅に上回る予測精度を示しています（例：5次元CSFの比較で、fvvdpCSFの7.92 dBに対し、stelaCSFは4.16 dB）。これは、stelaCSFが統計的に有意な改善をもたらしていることを意味します。

`stelaCSF`の独自の強みと貢献

stelaCSFは、これらの既存モデルと比較して、以下の点で優位性を持っています。

真の統一モデル: 空間周波数、時間周波数、輝度、偏心、面積という主要な5つの次元すべてを統一的に説明します。これにより、VR/ARアプリケーションなど、複数の次元を同時に考慮する必要がある場面での利用が可能になります。
複数のデータセットへの適合: 11の異なる研究からのデータを組み合わせ、単一のモデルで、同じパラメーターセットを使用してすべてのデータセットを予測できるように設計されています。これは、既存のCSFモデルが通常、個別のデータセットに適合するために再フィッティングを必要とするのとは対照的です。
広範なドメインでの精度: 低周波数を含む、各次元の全可視範囲で正確な予測を提供します（例：PoVの低周波数制限を克服）。
心理物理学的モデルに基づいた構築: 既知の心理物理学的モデル（Rovamo et al.の空間統合関係やWatsonの偏心効果など）および実験的証拠に基づいてモデルが構築されており、5つの次元間の主要な相互作用を説明できます。
公開されたデータセットとコード: モデルの構築に使用された大規模な標準化されたデータセットと、モデルのコードが公開されており、再現性とさらなる研究が促進されます。
アプリケーションでの実証: フリッカー検出アルゴリズムや中心窩レンダリングにおけるサンプリング係数の推定など、コンピューターグラフィックス分野での実用性が示されています。

制限事項

一方で、stelaCSFにもいくつかの制限があります。

高時間周波数での予測精度: CFF（臨界フリッカー融合周波数）の測定値など、非常に高い時間周波数での予測精度は、現状では不十分であると論文で述べられています（図19）。
輝度と偏心の相互作用: Koenderink et al. (1978) の研究で報告された、輝度と偏心間の相互作用（例：中心窩ではDeVries-Roseの法則に従って感度が低下するが、周辺部ではWeberの法則に従って一定に保たれる）は、モデル化されていません。
独立したデータセットでの検証: 多数のデータセットに適合させることでオーバーフィッティングのリスクは軽減されていますが、理想的には、トレーニングに使用されていない新しい独立したデータセットでモデルを検証する必要があります。
有彩色コントラスト感度: achromatic（無彩色）パターンに焦点を当てており、有彩色コントラスト感度（chromatic contrast sensitivity）は考慮されていません。

これらの比較から、stelaCSFが既存のCSFモデルの限界を克服し、多次元にわたる人間の視覚特性をより包括的かつ正確にモデル化しようとする、重要な一歩であることがわかります。

Q:提案手法の限界と今後の課題はなんですか？

A:

stelaCSFは、空間周波数、時間周波数、輝度、偏心、面積という5つの主要な次元にわたる人間のコントラスト感度を統一的にモデル化し、多くの既存モデルを上回る優れた予測性能を示していますが、完璧ではありません。論文では、以下の点が現在の限界として挙げられ、今後の課題として認識されています。

`stelaCSF`の限界

高時間周波数（特にCFF）での予測精度
- 現状: stelaCSFは、感度が$S=1$となる最高の時間周波数を見つけることでCFF（Critical Flicker Fusion frequency：臨界フリッカー融合周波数）の測定値を予測できるはずです。しかし、論文の図19に示すように、stelaCSFの予測はCFFデータと十分に一致していません。
- 具体的な課題:
  - 中程度の偏心でのCFFの増加: 中程度の偏心でCFFが増加するという傾向は、stelaCSFでは予測できません。この現象は、Krajancich et al. (2021) のデータだけでなく、Hartmann et al. (1979) やTyler and Hamer (1990) などの他のCFF測定でも報告されています。論文の著者は、この特性が低空間周波数、高時間周波数、および高輝度レベルでのみ観察されるのではないかと推測しています。
  - 非常に低い周波数での傾向の誤予測: 0.04 cpd以下の非常に低い空間周波数でも、CFFの傾向を正確に予測できていません。
- 示唆: stelaCSFの時間チャンネルモデル、または時間周波数と他の次元（特に偏心や空間周波数）との相互作用のモデル化が、高時間周波数域ではまだ不十分である可能性を示唆しています。
輝度と偏心の相互作用の欠如
- 現状: stelaCSFは、輝度と偏心の相互作用をモデル化していません。
- 具体的な課題: Koenderink et al. (1978) の研究では、移動するパターンに対するCSFが、中心窩ではDeVries-Roseの法則（低輝度で感度が輝度の平方根に比例して増加）に従って輝度とともに変化するのに対し、大きな偏心（最大50度）ではWeberの法則（感度が輝度から独立して一定）に従うことが発見されています。この効果は、Rovamo et al. (1995) の静的なGaborでは観察されなかったものの、特定の条件下の視覚に影響を与える重要な現象です。
- 示唆: stelaCSFの現状のモデルでは、網膜の異なる領域における輝度適応メカニズムの複雑な差異を完全に捉えることができていません。
独立した検証データの不足とオーバーフィッティングのリスク
- 現状: コントラスト感度データは、トレーニング用とテスト用に簡単に分割できるほど豊富ではありません。各データセットは通常、5次元空間の特定のスライスにわたる均一にサンプリングされたデータを含んでいます。
- 具体的な課題: 訓練データとテストデータを完全に分離しない場合、モデルが過剰に特定のデータセットに適合（オーバーフィッティング）してしまうリスクがあります。論文では、11のデータセットすべてに適合させ、データポイント数よりもはるかに少ないモデルパラメータを使用することで、このリスクを軽減していると述べています。
- 示唆: 理想的には、モデルはトレーニングに使用されていない、5次元空間からランダムにサンプリングされた新しい測定データセットで検証されるべきですが、このようなデータ収集は論文のスコープ外でした。これは、モデルの真の汎化能力を評価するための今後の重要な課題です。
有彩色コントラスト感度の欠如
- 現状: stelaCSFは、achromatic（無彩色）コントラスト感度に特化しています。
- 具体的な課題: Mantiuk et al. (2020) やWuerger et al. (2020) の研究にあるように、人間の視覚系は色（chromatic）のコントラストにも感度を持っており、これは輝度（luminance）のコントラストとは異なる特性を示します。特に、VR/ARディスプレイでは広色域や高輝度が一般的になっており、色知覚の正確なモデル化がますます重要になっています。
- 示唆: stelaCSFは、現代のディスプレイ技術の要件を完全に満たすためには、有彩色成分を統合する必要があります。論文の著者らは、castleCSF (Ashraf et al.) としてこの方向で研究を進めていることを示唆する引用を他の論文で行っています。

今後の課題と研究の方向性

上記の限界を踏まえ、stelaCSFの今後の課題と研究の方向性としては、以下のような点が考えられます。

CFF予測の改善:
- 高時間周波数域におけるモデルの精度を向上させるために、既存のCFFデータセットをさらに詳細に分析し、必要に応じて新たな心理物理学的測定を行うことが考えられます。
- 時間応答モデル（式11, 12）や、時間周波数と他の次元（特に偏心、空間周波数、輝度）の相互作用を表す項を修正・追加することが考えられます。例えば、中程度の偏心でのCFFの増加を説明するメカニズムの導入などです。
輝度と偏心の相互作用のモデル化:
- Koenderink et al. (1978) の知見を取り入れ、輝度と偏心間の相互作用をモデルに追加することで、異なる網膜領域での適応特性の差異をより正確に反映させることが可能です。これは、特に幅広い輝度と視野を持つAR/VRアプリケーションにとって重要です。
独立した大規模な検証データセットの構築:
- モデルの汎化能力を厳密に評価するため、5次元空間を体系的かつランダムにサンプリングした、トレーニングに用いられていない新しい大規模な心理物理学的データセットを収集することが理想的です。
有彩色コントラスト感度の統合:
- stelaCSFを無彩色だけでなく、有彩色コントラスト感度も含むように拡張することで、より包括的な視覚モデルを構築できます。これにより、色歪みや色のフリッカーなど、現代のディスプレイにおける多様な視覚アーティファクトの評価に対応できるようになります。
より複雑な視覚モデルへの組み込み:
- stelaCSFは、低コントラストでしきい値に近い違いを予測するためのビルディングブロックとして機能します。しかし、高コントラストのパターンやパターン化された背景における知覚をモデル化するには、コントラスト恒常性やコントラストマスキングを考慮したVDP（Visual Difference Predictor）やHDR-VDPのようなより複雑な視覚モデルと統合する必要があります（セクション7.1）。
動的な視覚特性の考慮:
- 眼球運動（サッケード、スムースパーシュートなど）や頭部運動が、提示される刺激の有効な空間・時間周波数、偏心にどのように影響するかを考慮することで、モデルの現実世界での適用可能性をさらに高めることができます。