Python １次元でのDMD

はじめに

動的モード分解（Dynamic Mode Decomposition; DMD）というものが、2008年に発表されています¹²。DMDは主成分分析とフーリエ変換をあわせたような分解方法で、データを次元と時間方向の特徴に分離できる手法です。

参考にした解説記事は以下にあります。

• http://www.pyrunner.com/weblog/2016/07/25/dmd-python/
• https://iqujack-lequina.hatenablog.com/entry/2018/05/20/動的モード分解に関する覚書
• https://qiita.com/Miyabi1456/items/702f62c9bcd9c063d664
• https://qiita.com/harmegiddo/items/84552c32f4b75c26878a

DMDの固有値、固有ベクトルは複素数になり、固有値の複素成分で時間方向の分解を表します。ただ、１次元定在波だとうまく分離できない問題があります。説明は以下の記事にあります。

• https://iqujack-lequina.hatenablog.com/entry/2018/12/02/定在波のDMD

Pythonコードが公開されていなかったので、参考までに記載します。うまく分解できない例と、できる例を示します。ベースとなる論文はTu 2014³で、コードは、DMDの本のMatlabコードを参考にしています。

環境

• Windows 10 home

• Anaconda(Python 3.7.6)

• Numpy(1.18.1)

分解対象

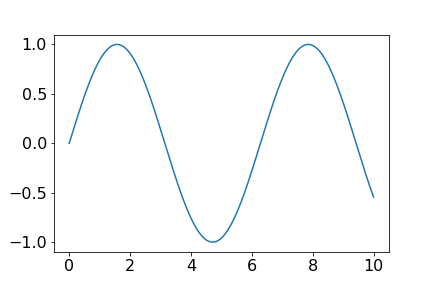
１次元のサイン波の数値データから周期を見つけます。周期は、複素数だと$1j$ですね。
$$
y = \sin(x)
$$

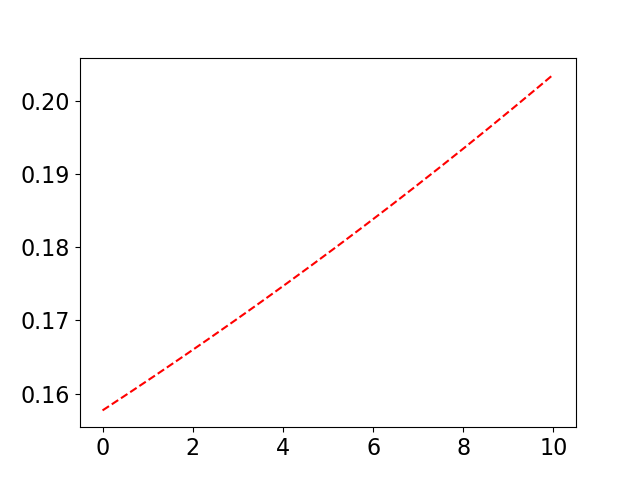
うまくいかないDMD例

うまくいかない例では、データが１次元しかないため、固有値が実数になり、複素数が出てきません。そのため、周期成分が分解できません。

import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt
%matplotlib inline

t = np.arange(0, 10.01, 0.01)
x = np.sin(t)
dt = t[2] - t[1]

#データ行列
X1 = x[:-1]
X2 = x[1:]

#SVD
U,S,Vh = LA.svd(X1[np.newaxis,:],False)
V = Vh.T

#Aを左特異ベクトルで次元削減したAtilde
Atilde = np.dot(np.dot(np.dot(U.T, X2[np.newaxis,:]), V), LA.inv(np.diag(S)))

#Atilde の固有値と固有ベクトルを求める
Lam, W = LA.eig(Atilde)

print("固有値:",Lam)#Lam:1.00025541となって実数

#Atildeの固有ベクトルから、Aの固有ベクトルを求める
Phi = np.dot(np.dot(np.dot(X2[np.newaxis,:], V), LA.inv(np.diag(S))), W)

#離散型から連続型のexp(**)の**を求める
Omega = np.log(Lam)/dt

#OmegaとPhiから元の関数を復元する。
b = np.dot(LA.pinv(Phi * np.exp(Omega * t)).T, x)
x_dmd = b * Phi * np.exp(Omega * t)

plt.plot(t, x_dmd[0,:])
plt.show()

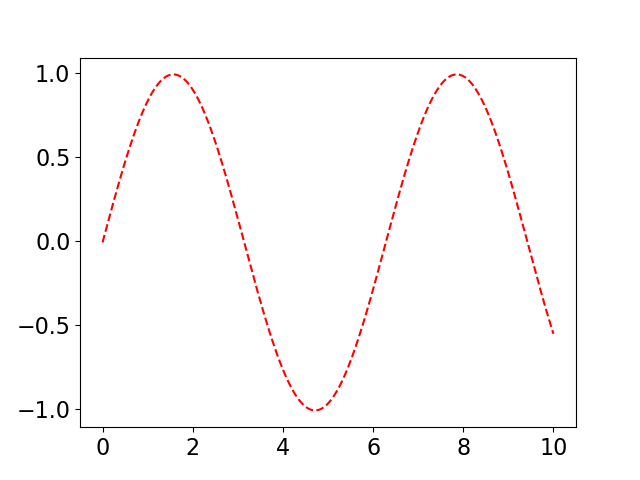
うまくいくDMD例

説明記事で紹介されていますが、時間方向にデータをずらしたもので、もう一次元作り、２次元データにします。こうすることで、固有値に複素成分が出まして、数値データから、$\sin(x)$ が見つけられます。ただ、それだけです。

import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt
%matplotlib inline

t = np.arange(0, 10.01, 0.01)
x = np.sin(t)
dt = t[2] - t[1]

#データ行列
#主な違いはここです。２次元にしています。
X_aug1 = np.array([x[:-2], x[1:-1]])
X_aug2 = np.array([x[1:-1], x[2:]])

#SVD
U,S,Vh = LA.svd(X_aug1,False)
V = Vh.conj().T

#Aを左特異ベクトルで次元削減したAtilde
#Uは複素共役をとって、転置行列にしてます。
Atilde = np.dot(np.dot(np.dot(U.conj().T, X_aug2), V), LA.inv(np.diag(S)))

#Atilde の固有値と固有ベクトルを求める
Lam, W = LA.eig(Atilde)

print("固有値:", Lam)#Lam:[0.9995+0.00999983j 0.9995-0.00999983j]複素数

#Atildeの固有ベクトルから、Aの固有ベクトルを求める
Phi = np.dot(np.dot(np.dot(X_aug2, V), LA.inv(np.diag(S))), W)

#離散型から連続型のexp(**)の**を求める
Omega = np.diag(np.log(Lam)/dt)

print("Omega:", Omega)#念のため、1jになる

#OmegaとPhiから元の関数を復元する。
#やっていることは１次元と変わらないですが、書き方が異なります。
b = np.dot(LA.pinv(Phi), X_aug1[:,0])
x_dmd = np.zeros([2,len(t)], dtype='complex')
for i, _t in enumerate(t):
    x_dmd[:,i] = np.dot(np.dot(Phi, np.exp(Omega * _t)), b)

plt.plot(t, x_dmd[0,:].real)
plt.show()

参考文献

1. P.J. Schmid, "Dynamic Mode Decomposition of numerical and experimental data", Proc., 61st Annual Meeting of the APS Division of Fluid Dynamics, 2008. ↩

2. P.J. Schmid, "Dynamic mode decomposition of numerical and experimental data", Journal of Fluid Mechanics, 2010. ↩

3. Tu, Rowley, Luchtenburg, Brunton, and Kutz, "On Dynamic Mode Decomposition: Theory and Applications", *American Institute of Mathematical Sciences, 2014. ↩