動的モード分解(Dynamic Mode Decomposition)のご紹介

はじめに

時間変化を調べる方法といえばフーリエ変換かウェーブレット変換くらいしか思い浮かびませんでしたが、時間方向と空間方向双方のモードを抽出できる動的モード分解(DMD)という良い手法があることを知りました。自身の理解を深めるためにもここに記録しようと思います。

内容はほぼ参考にしたサイトそのままで、Google翻訳したものを少し直して書いていきます。グラフ描画に関するコードは参考元にはないので追記しておきました。DMDの実行からグラフの描画までそのまま実行できるはずです。

参考

簡単のために3次元ベクトル場のDMDは省略して、単純な1次元のスカラー関数のみを考えます。
Dynamic Mode Decomposition in Python

SVDもなんだか知らなかったのでこちらを参考にしました。
PCAとSVDの関連について

動的モード分解

動的モード分解(DMD)は、比較的最近の数学的革新であり、とりわけ、時間内に成長、減衰、および/または振動するコヒーレント構造に関して動的システムを解決または近似することができます。コヒーレント構造をDMDモードと呼びます。各DMDモードには、単一の固有値に関して定義された対応する時間ダイナミクスがあります。

言い換えれば、DMDは動的システムを固有値によってダイナミクスが支配されるモードの重ね合わせに変換します。

驚くべきことに、DMDモードと固有値を識別するための数学的手順は純粋に線形ですが、システム自体は非線形でも構いません。ここでは取り上げませんが、非線形システムはモードと固有値のペアのセットで記述できるという主張には、健全な理論的根拠があります。詳細については、Koopman演算子とDMDの連携に関する論文を読んでください¹²³。

DMDは、システムの内部動作を分析するための便利な診断ツールであるだけでなく、システムの将来の状態を予測するためにも使用できます。必要なのは、モードと固有値だけです。僅かな労力で、モードと固有値を組み合わせて、いつでもシステム状態を近似する関数を生成できます。

公式の定義

n個のデータセットを考えます。
$${(x_0,y_0),(x_1,y_1),\dots (x_n,y_n)}$$

ここで、$x_i$と$y_i$はそれぞれ大きさ$m$の列ベクトルです。2つの$m\times n$行列を定義します。
$$X=[x_0\ x_1\ \dots\ x_n],\quad Y=[y_0\ y_1\ \dots\ y_n]$$

演算子$A$を次のように定義すると
$$A=YX^\dagger$$

ここで、$X^\dagger$は$X$の疑似逆行列であり、$(X,Y)$の動的モード分解は$A$の固有値分解によって与えられます。つまりDMDモードと固有値は$A$の固有ベクトルと固有値です。

上記のTu et al.²による定義はexact DMDとして知られています。これは現在最も一般的な定義であり、特定の要件を満たす任意のデータセットに適用できます。この記事では、$A$がすべての$i$について式$y_i=Ax_i$を（おそらくおおよそ）満たす場合に最も興味があります。または、より正確には:
$$Y=AX$$

明らかに、$X$は入力ベクトルのセットであり、$Y$は対応する出力ベクトルのセットです。このDMDの特定の解釈は、支配方程式が不明な動的すステムを分析（および予測）するための便利な方法を提供するため、非常に強力です。動的システムについては後ほど説明します。

このDMD²の定義に沿った定理がいくつかあります。より有用な定理の1つは、$X$と$Y$が線形に一貫している場合（換言すれば、ベクトル$v$に対して$Xv=0$であるとき、常に$Yv=0$も満たす場合）に限り、$Y=AX$を完全に満たします。後で説明するように、線形一貫性のテストは比較的簡単です。つまり、線形一貫性はDMDを使用するための必須の前提条件ではありません。$A$のDMD分解が式$Y=AX$を完全に満たさない場合でも、最小二乗法であり、$L^2$ノルムの誤差を最小にします。

DMDアルゴリズム

一見すると、$A=YX^\dagger$の固有値分解はそれほど大きな問題ではないように思えます。実際、$X$と$Y$のサイズが適切な場合、NumpyまたはMATLABからpinvメソッドとeigメソッドを2、3回呼び出すとうまくいきます。問題は$A$が本当に大きいときに発生します。$A$は$m\times m$であるため、$m$（各時間サンプル内の信号の数）が非常に大きい場合、固有値分解が扱いにくくなります。

幸いなことに、exact DMDのアルゴリズムの助けを借りて、問題を小さな断片に分割することができます。

1. $X$のSVD(singular value decomposition:特異値分解)を計算し、同時に必要に応じて低位の切り捨てを実行します:
   $$X=U\Sigma V^*$$

2. 行列$A$を$U$へ射影して$\tilde A$を計算します:
   $$\tilde A=U^* AU=U^*YV\Sigma^{-1}$$

3. $\tilde A$の固有値$\lambda_i$と固有ベクトル$w_i$を計算します:
   $$\tilde AW=W\Lambda$$

4. $W$と$\Lambda$から$A$の固有値分解を再構成します。$A$の固有値は、$\tilde A$の固有値と同等です。$A$の固有ベクトルは、$\Phi$の列で与えられます。
   $$A\Phi=\Phi\Lambda,\quad \Phi=YV\Sigma^{-1}W$$

アルゴリズムの導出のより詳細な説明は、参考文献¹²にあります。また、$\Phi=UW$は、projected DMDモードと呼ばれる$\Phi$の代替の導出であることに注意することも理論的に興味深いかもしれません。この記事では、exact DMDモードのみを使用します。

Pythonでアルゴリズムをステップごとに見ていきましょう。 必要なすべてのパッケージをインストールしてインポートすることから始めます。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from numpy import dot, multiply, diag, power
from numpy import pi, exp, sin, cos, cosh, tanh, real, imag
from numpy.linalg import inv, eig, pinv
from scipy.linalg import svd, svdvals
from scipy.integrate import odeint, ode, complex_ode
from warnings import warn

#これは私の好み
plt.rcParams["font.family"] = "Times New Roman"      #全体のフォントを設定
plt.rcParams["xtick.direction"] = "in"               #x軸の目盛線を内向きへ
plt.rcParams["ytick.direction"] = "in"               #y軸の目盛線を内向きへ
plt.rcParams["xtick.minor.visible"] = True           #x軸補助目盛りの追加
plt.rcParams["ytick.minor.visible"] = True           #y軸補助目盛りの追加
plt.rcParams["xtick.major.width"] = 1.5              #x軸主目盛り線の線幅
plt.rcParams["ytick.major.width"] = 1.5              #y軸主目盛り線の線幅
plt.rcParams["xtick.minor.width"] = 1.0              #x軸補助目盛り線の線幅
plt.rcParams["ytick.minor.width"] = 1.0              #y軸補助目盛り線の線幅
plt.rcParams["xtick.major.size"] = 10                #x軸主目盛り線の長さ
plt.rcParams["ytick.major.size"] = 10                #y軸主目盛り線の長さ
plt.rcParams["xtick.minor.size"] = 5                 #x軸補助目盛り線の長さ
plt.rcParams["ytick.minor.size"] = 5                 #y軸補助目盛り線の長さ
plt.rcParams["font.size"] = 14                       #フォントの大きさ
plt.rcParams["axes.linewidth"] = 1.5                 #囲みの太さ

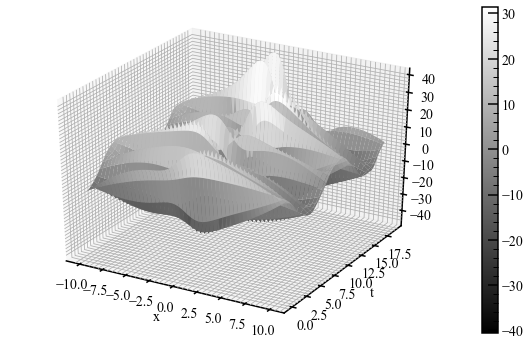
いくつかのプレイデータを生成しましょう。 実際には、必ずしもデータの支配方程式を知っているわけではないことに注意してください。 ここでは、データセットを作成するための方程式をいくつか作成しています。 データが生成されたら、それらが存在することを忘れてください。

# 時間領域と空間領域を定義する
x = np.linspace(-10, 10, 100)
t = np.linspace(0, 6*pi, 80)
dt = t[2] - t[1]
Xm,Tm = np.meshgrid(x, t)

# 3つの時間と空間上のパターンを作成する
f1 = multiply(20-0.2*power(Xm, 2), exp((2.3j)*Tm))
f2 = multiply(Xm, exp(0.6j*Tm))
f3 = multiply(5*multiply(1/cosh(Xm/2), tanh(Xm/2)), 2*exp((0.1+2.8j)*Tm))

# 信号を組み合わせてデータ行列を作成する
D = (f1 + f2 + f3).T

# DMD入出力行列を作成する
X = D[:,:-1]
Y = D[:,1:]

fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111, projection="3d")
surf = ax.plot_surface(Xm, Tm, np.real(D.T), cmap="gray", linewidth=0)
ax.set_xlabel("x")
ax.set_ylabel("t")
fig.colorbar(surf)

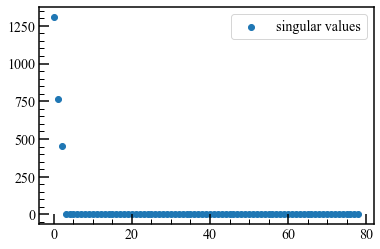
ここで、$X$のSVDを計算します。主な関心のある最初の変数は、$X$の特異値である$\Sigma$です。$X$のSVDを取得すると、「高エネルギー」モードを抽出し、システムの次元を適切な直交分解で削減できます （Proper Orthogonal Decomposition, POD:固有直交分解）。 特異値を見ると、切り捨てるモードの数が決まります。

# 入力行列のSVD
U2,Sig2,Vh2 = svd(X, False)

fig, ax = plt.subplots()
ax.scatter(range(len(Sig2)), Sig2, label="singular values")
ax.legend()

上記の特異値を考えると、データには重要な3つのモードがあると結論付けられます。 したがって、これらのモードのみを含めるようにSVDを切り捨てます。 次に、$\tilde A$を構築し、その固有値分解を見つけます。

# ランク3切り捨て
r = 3
U = U2[:,:r]
Sig = diag(Sig2)[:r,:r]
V = Vh2.conj().T[:,:r]

# A~を構築する
Atil = dot(dot(dot(U.conj().T, Y), V), inv(Sig))
mu,W = eig(Atil)

def circle(r=1):
    x,y = [],[]
    for _x in np.linspace(-180,180,360):
        x.append(np.sin(np.radians(_x)))
        y.append(np.cos(np.radians(_x)))
    return x,y

c_x,c_y = circle(r=1)

fig, ax = plt.subplots(figsize=(8,8))
ax.plot(c_x, c_y, c="k", linestyle="dashed")
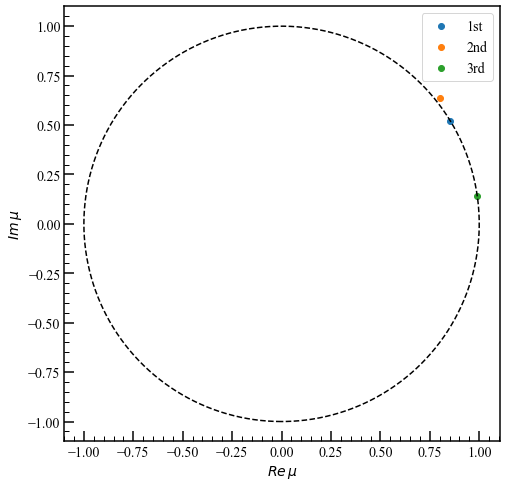
ax.scatter(np.real(mu[0]), np.imag(mu[0]), label="1st")
ax.scatter(np.real(mu[1]), np.imag(mu[1]), label="2nd")
ax.scatter(np.real(mu[2]), np.imag(mu[2]), label="3rd")
ax.set_aspect("equal")
ax.set_xlabel(r"$\it{Re}\,\mu$")
ax.set_ylabel(r"$\it{Im}\,\mu$")
ax.legend()

$\Lambda$の各固有値は、対応するDMDモードの動的な振る舞いについて教えてくれます。 その正確な解釈は、$X$と$Y$の関係の性質に依存します。差分方程式の場合、多くの結論を出すことができます。 固有値にゼロ以外の虚数部がある場合、対応するDMDモードに振動があります。 固有値が単位円内にある場合、モードは減衰しています。 固有値が外側にある場合、モードは成長しています。 固有値が単位円に正確に当てはまる場合、モードは成長も減衰もしません。

次に、exact DMDモードを構築します。

# DMDモードを構築する
Phi = dot(dot(dot(Y, V), inv(Sig)), W)

fig, ax = plt.subplots()
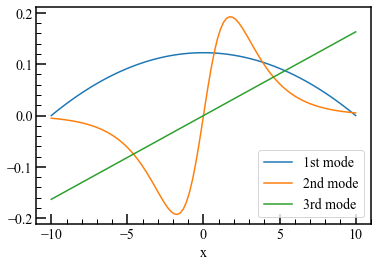
ax.plot(x, np.real(Phi[:,0]), label="1st mode")
ax.plot(x, np.real(Phi[:,1]), label="2nd mode")
ax.plot(x, np.real(Phi[:,2]), label="3rd mode")
ax.set_xlabel("x")
ax.legend()

$\Phi$の列は、上にプロットされたDMDモードです。 それらは、異なる時間ダイナミクスに従ってシステム内で成長/減衰/振動する一貫した構造です。 上記のプロットの曲線を、元の3D表面プロットに見られる回転、進化する形状と比較します。 類似点に気付くはずです。

ここがDMDアルゴリズムの技術的な終着点です。 $A$の固有値分解とシステム$Y=AX$の性質の基本的な理解を備えているため、システムの時間発展に対応する行列$\Psi$を構築できます。 以下のコードを完全に理解するには、次のセクションで差分方程式の関数$x(t)$を見てください。

# 時間発展の計算
b = dot(pinv(Phi), X[:,0])
Psi = np.zeros([r, len(t)], dtype='complex')
for i,_t in enumerate(t):
    Psi[:,i] = multiply(power(mu, _t/dt), b)

fig = plt.figure(figsize=(10,10))
ax1,ax2,ax3 = fig.add_subplot(311), fig.add_subplot(312), fig.add_subplot(313)
plt.subplots_adjust(wspace=0.5, hspace=0.5)
ax1.set_title("1st mode"), ax2.set_title("2nd mode"), ax3.set_title("3rd mode")

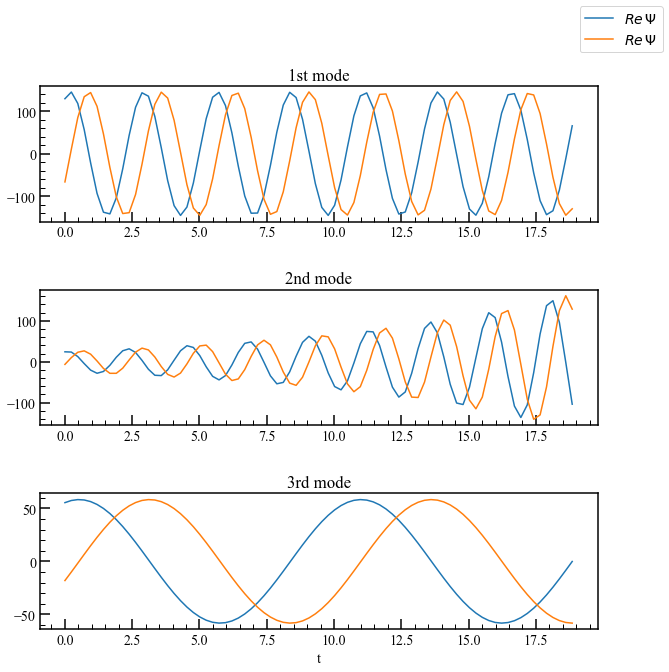
ax1.plot(t, np.real(Psi[0]), label=r"$\it{Re}\,\Psi$")
ax1.plot(t, np.imag(Psi[0]), label=r"$\it{Re}\,\Psi$")
ax2.plot(t, np.real(Psi[1])), ax2.plot(t, np.imag(Psi[1]))
ax3.plot(t, np.real(Psi[2])), ax3.plot(t, np.imag(Psi[2]))
ax3.set_xlabel("t")

fig.legend()

上記の3つのプロットは、3つのDMDモードの時間ダイナミクスです。 3つすべてが振動していることに注目してください。 さらに、2番目のモードは指数関数的に成長するように見えます。これは固有値プロットによって確認されます。

元のデータ行列の近似を作成する場合は、単純に$\Phi$と$\Psi$を乗算します。 この特定のケースでは、オリジナルと近似が正確に一致します。

# DMD再構成の計算
D2 = dot(Phi, Psi)
np.allclose(D, D2) # True

動的システム

この記事では、式$Y=AX$の2つの解釈のみを検討します。 最初の解釈は、$A$が差分方程式を定義する場所で
$$x_{i+1}=Ax_i$$

この場合、演算子$A$は動的システム状態$x_i$を時間的に1ステップ進めます。 時系列$D$があるとしましょう。
$$D=[x_0\ x_1\ \dots\ x_{n+1}]$$

ここで、$x_i$はタイムステップ$i$でのシステムの$m$次元状態を定義する列ベクトルです。すると、以下のように$X$と$Y$を定義できます。
$$X=[x_0\ x_1\ \dots\ x_{n}],\quad Y=[x_1\ x_2\ \dots\ x_{n+1}]$$

このようにして、$X$および$Y$の列ベクトルの各組は、差分方程式の1回の反復に対応し、一般に次のようになります。
$$Y=AX$$

DMDを使用して、$A\Phi=\Phi\Lambda$の固有分解を見つけます。 DMDモードと固有値を使用すると、$Y=AX$を時間ステップ$\Delta t$の離散時間反復$k$で定義された関数に簡単に変換できます。
$$x_k=\Phi\Lambda^k\Phi^\dagger x_0$$

連続時間$t$の対応する関数は
$$x(t)=\Phi\Lambda^{t/\Delta t}\Phi^\dagger x(0)$$

本当に驚くべきことは、データのみを使用して時間内に明示的な関数を定義したところです。これは、方程式のないモデリングの良い例です。

この記事で考慮される$Y=AX$の2番目の解釈は、$A$が微分方程式系を定義する場所で
$$\dot x=Ax$$

この場合、演算子$A$は、ベクトル$x_i$の時間に関する1次導関数を計算します。 行列$X$と$Y$は、ベクトル場の$n$個のサンプルで構成されます。$X$の$i$番目の列は位置ベクトル$x_i$です。 $Y$の$i$番目の列は、速度ベクトル$\dot x_i$です。

DMDの計算後、時間の関数は先程と非常によく似ています（つまり、差分方程式）。 $x(0)$が任意の初期条件であり、$t$が連続時間である場合、
$$x(t)=\Phi\text{exp}(\Lambda t)\Phi^\dagger x(0)$$

ヘルパーメソッド

便宜上、DMDコードを1つのメソッドにまとめて、いくつかのヘルパーメソッドを定義して線形整合性をチェックし、解を確認します。

def nullspace(A, atol=1e-13, rtol=0):
    # from http://scipy-cookbook.readthedocs.io/items/RankNullspace.html
    A = np.atleast_2d(A)
    u, s, vh = svd(A)
    tol = max(atol, rtol * s[0])
    nnz = (s >= tol).sum()
    ns = vh[nnz:].conj().T
    return ns

def check_linear_consistency(X, Y, show_warning=True):
    # tests linear consistency of two matrices (i.e., whenever Xc=0, then Yc=0)
    A = dot(Y, nullspace(X))
    total = A.shape[1]
    z = np.zeros([total, 1])
    fails = 0
    for i in range(total):
        if not np.allclose(z, A[:,i]):
            fails += 1
    if fails > 0 and show_warning:
        warn('linear consistency check failed {} out of {}'.format(fails, total))
    return fails, total

def dmd(X, Y, truncate=None):
    U2,Sig2,Vh2 = svd(X, False) # SVD of input matrix
    r = len(Sig2) if truncate is None else truncate # rank truncation
    U = U2[:,:r]
    Sig = diag(Sig2)[:r,:r]
    V = Vh2.conj().T[:,:r]
    Atil = dot(dot(dot(U.conj().T, Y), V), inv(Sig)) # build A tilde
    mu,W = eig(Atil)
    Phi = dot(dot(dot(Y, V), inv(Sig)), W) # build DMD modes
    return mu, Phi

def check_dmd_result(X, Y, mu, Phi, show_warning=True):
    b = np.allclose(Y, dot(dot(dot(Phi, diag(mu)), pinv(Phi)), X))
    if not b and show_warning:
        warn('dmd result does not satisfy Y=AX')

制限事項

DMDにはいくつかの既知の制限があります。 まず第一に、並進および回転の不変性を特にうまく処理できません。 第二に、一時的な時間動作が存在する場合、完全に失敗する可能性があります。 次の例は、これらの問題を示しています。

1. 並進不変性

次のデータセットは非常に単純です。 これは、システムの進化に応じて空間ドメインに沿って並進する単一モード（ガウス）で構成されます。 DMDはこれをきれいに処理すると思うかもしれませんが、逆のことが起こります。 SVDは、明確に定義された単一の特異値を取得する代わりに、多くの値を取得します。

# 時間領域と空間領域を定義する
x = np.linspace(-10, 10, 50)
t = np.linspace(0, 10, 100)
dt = t[2] - t[1]
Xm,Tm = np.meshgrid(x, t)

# 空間的にも時間的にも移動する単一モードでデータを作成する
D = exp(-power((Xm-Tm+5)/2, 2))
D = D.T

# 入出力行列を抽出する
X = D[:,:-1]
Y = D[:,1:]
check_linear_consistency(X, Y)

U2,Sig2,Vh2 = svd(X, False)

fig = plt.figure(figsize=(10,5))
ax1,ax2 = fig.add_subplot(121), fig.add_subplot(122)
ax1.set_xlabel("x"), ax1.set_ylabel("t")
ax1.imshow(D.T, aspect=0.5)
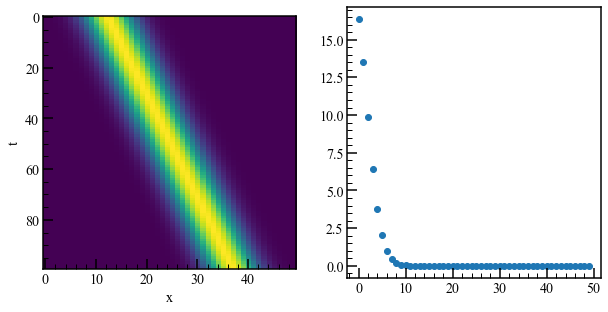
ax2.scatter(range(len(Sig2)), Sig2)

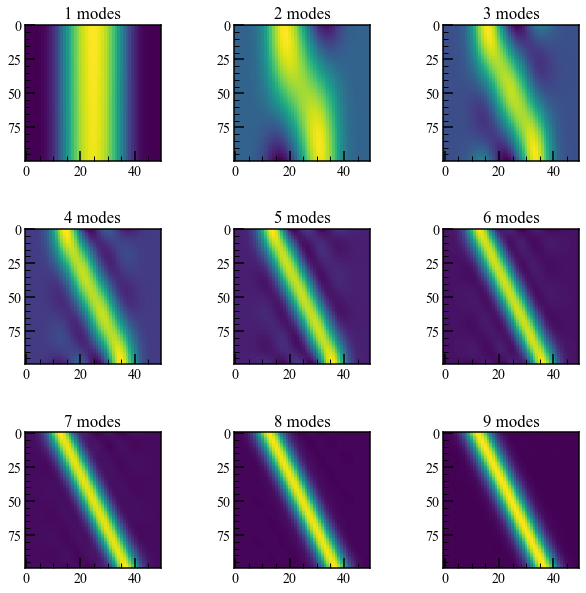
左側のプロットは、システムの時間変化を示しています。 右側のプロットは特異値を示しています。 システムを正確に近似するには、10近いDMDモードが必要であることがわかりました。次のプロットを考えてみましょう。真のダイナミクスと、重ね合わせるモードの数を変化させたものを比較します。

def build_dmd_modes(t, X, Y, r):
    """
    DMD再構成
    """
    mu, Phi = dmd(X, Y, truncate=r)
    b = dot(pinv(Phi), X[:,0])
    Psi = np.zeros([r, len(t)], dtype='complex')
    for i,_t in enumerate(t):
        Psi[:,i] = multiply(power(mu, _t/dt), b)
    return dot(Phi, Psi)

fig = plt.figure(figsize=(10,10))
axes = []
for i in range(9):
    axes.append(fig.add_subplot(331+i))
plt.subplots_adjust(wspace=0.5, hspace=0.5)

for i,ax in enumerate(axes):
    ax.set_title("{} modes".format(i+1))
    ax.imshow(np.real(build_dmd_modes(t, X, Y, r=i+1).T), aspect=0.5)

2. 過渡時間の挙動

この最後の例では、一時的な時間のダイナミクスを含むデータセットを調べます。 具体的には、データにガウスが存在する場合と存在しない場合を示しています。 残念ながら、DMDはこのデータを正確に分解できません。

# 時間領域と空間領域を定義する
x = np.linspace(-10, 10, 50)
t = np.linspace(0, 10, 100)
dt = t[2] - t[1]
Xm,Tm = np.meshgrid(x, t)

# 単一の一時モードでデータを作成する
D = exp(-power((Xm)/4, 2)) * exp(-power((Tm-5)/2, 2))
D = D.astype('complex').T

# 入出力行列を抽出する
X = D[:,:-1]
Y = D[:,1:]
check_linear_consistency(X, Y)

# DMD分解
r = 1
mu,Phi = dmd(X, Y, r)
check_dmd_result(X, Y, mu, Phi)

# 時間発展
b = dot(pinv(Phi), X[:,0])
Psi = np.zeros([r, len(t)], dtype='complex')
for i,_t in enumerate(t):
    Psi[:,i] = multiply(power(mu, _t/dt), b)

fig = plt.figure(figsize=(10,10))
ax1,ax2 = fig.add_subplot(221),fig.add_subplot(222)
ax3,ax4 = fig.add_subplot(223),fig.add_subplot(224)

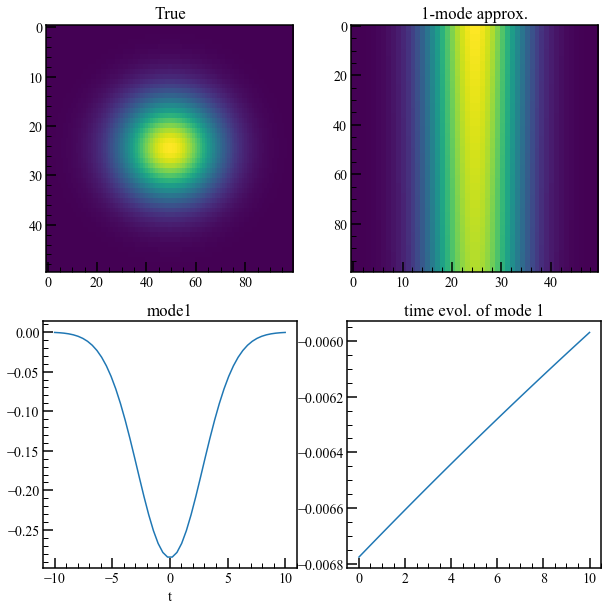
ax1.imshow(np.real(D), aspect=2.0), ax1.set_title("True")
ax2.imshow(np.real(dot(Phi, Psi).T), aspect=0.5), ax2.set_title("1-mode approx.")
ax3.plot(x, np.real(Phi)), ax3.set_xlabel("x"), ax3.set_title("mode1")
ax4.plot(t, np.real(Psi[0])), ax3.set_xlabel("t"), ax4.set_title("time evol. of mode 1")

DMDはモードを正しく識別しますが、時間の振る舞いを完全に識別することはできません。 これは、DMD時系列の時間挙動が固有値に依存していることを考慮すると理解できます。固有値は、指数関数的成長（固有値の実数部）と振動（虚数部）の組み合わせのみを特徴付けることができます。

このシステムの興味深い点は、理想的な分解がさまざまな固有値を持つ単一モード（図に示すように）の重ね合わせで構成される可能性があることです。 単一のモードに、真の時間ダイナミクスを近似する多くの直交サインとコサインの線形結合（フーリエ級数）が掛けられていると想像してください。 残念ながら、SVDベースのDMDの単一のアプリケーションでは、異なる固有値で同じDMDモードを何度も生成することはできません。

さらに、時間の振る舞いを多数の固有値として正しく抽出できたとしても、過渡的な振る舞い自体を完全に理解しないと、解の予測機能は信頼できないことに注意することが重要です。 一時的な動作は、その性質上、永続的ではありません。

多重解像度DMD（mrDMD）は、DMDを再帰的に適用することにより、一時的な時間動作の問題を軽減しようとしています。

結言

その制限にもかかわらず、DMDは動的システムを分析および予測するための非常に強力なツールです。 すべてのバックグラウンドのすべてのデータサイエンティストは、DMDとその適用方法について十分に理解している必要があります。 この記事の目的は、DMDの背後にある理論を提供し、実際のデータで使用できる実用的なPythonのコード例を提供することです。 DMDの正式な定義を検討し、アルゴリズムを段階的に説明し、失敗した例を含むいくつかの簡単な使用例を試してみました。これにより、DMDが研究プロジェクトまたはエンジニアリングプロジェクトにどのように適用されるかについて、より明確な理解が得られることを願っています。

DMDには多くの拡張機能があります。 将来の作業では、多解像度DMD（mrDMD）やスパースDMD（sDMD）など、これらの拡張機能の一部に関する投稿が行われる可能性があります。

まとめ

ハイスピードカメラの映像のような2次元配列の時間発展をDMDしようと思ったときは、2次元配列を1次元配列に平らにすれば上記のコードでうまくいきます。CFDでカルマン渦のシミュレーションをしたものをDMDした例もそのうち追加しようと思います。

1. "Kutz, J. Nathan. Data-driven modeling & scientific computation: methods for complex systems & big data. OUP Oxford, 2013" ↩ ↩²

2. "Tu, Jonathan H., et al. “On dynamic mode decomposition: theory and applications.” arXiv preprint arXiv:1312.0041 (2013)." ↩ ↩² ↩³ ↩⁴

3. "Wikipedia contributors. “Composition operator.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 28 Dec. 2015. Web. 24 Jul. 2016." ↩