DMD(dynamic mode decomposition; 動的モード分解)に入門する

0. 概要

DMD(dynamic mode decomposition)は時系列データから固定の周波数及び時系列変化（減衰、成長）を解析してくれる、とりわけ新しい数式理論（2008年に登場）である。主成分分析(PCA)と異なる次元削減アルゴリズムだと考えればよい。特徴は、PCAよりは縮約モデルとしての削減率は低いが、正弦波をベースに分解されるので物理的な意味合いが強くなる傾向がある。

約まるところ、フーリエ変換と似た動作をする。また、縮約モデルとしても機能する。
※2018年現在解説記事が殆どないので間違っていた場合は指摘をお願いします。

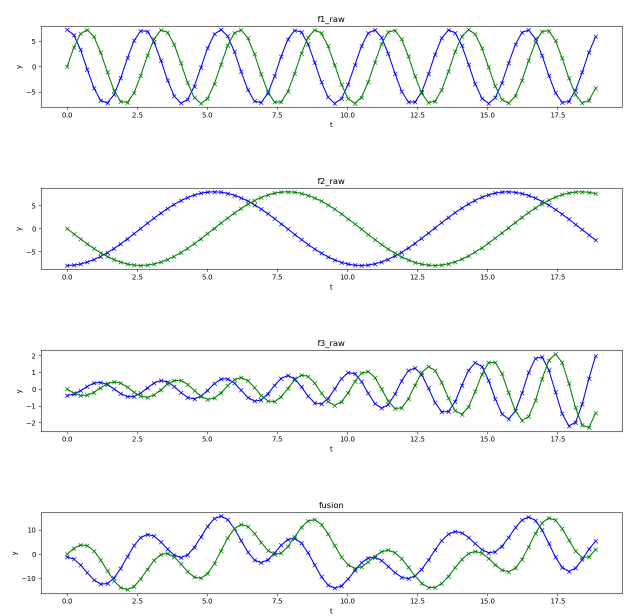
具体例としては、3つの波形が合わさった合成波があったとする。

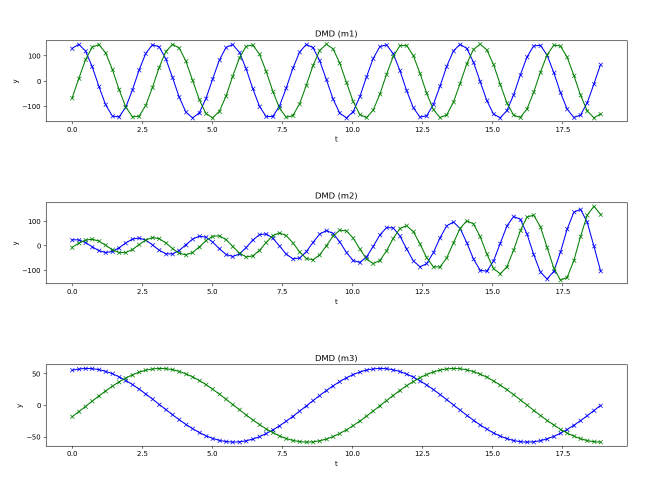
それをDMDによって分解すると、以下のような波形が得られる。この3つを重ね合わせれば元の合成波となる。

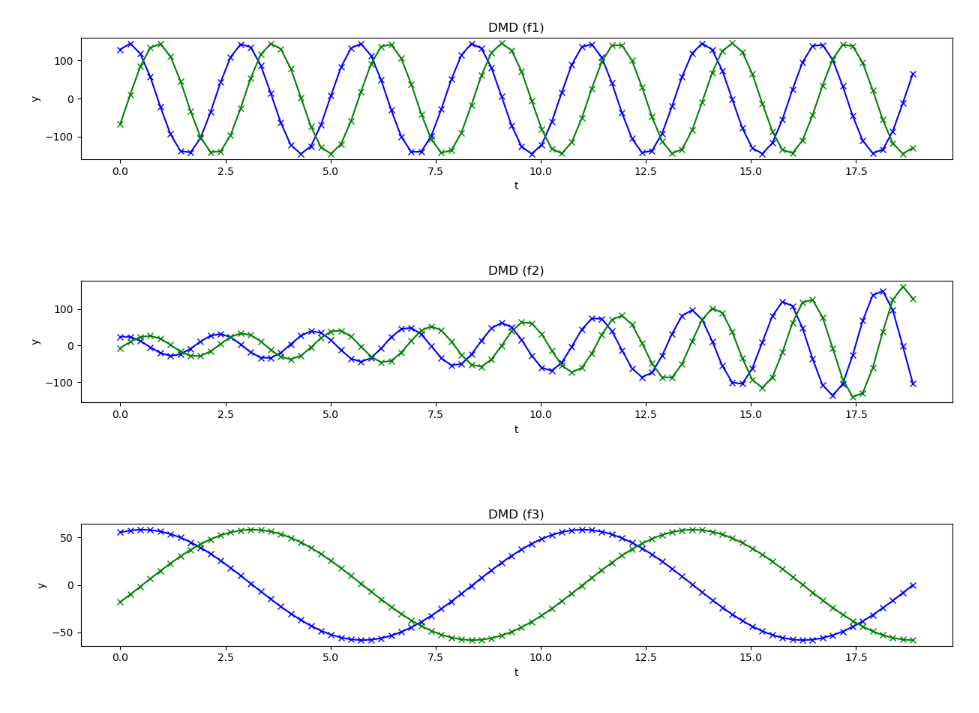
これは波や音声等あらゆる波形を分析する際に用いることが出来る。

参考文献:
http://www.pyrunner.com/weblog/2016/07/25/dmd-python/

1. 理論

DMDで扱うデータ及びアルゴリズムについて説明する。

1.1 データ

DMDでは時系列データを用い、時間発展させていく。

1.1.1 スナップショットデータ

DMDはフローデータ(時系列データ)から動的特徴を抽出する手法である。このため、用いるデータは時系列である。
ある時刻における状態ベクトル(1次元)をスナップショットという。
スナップショットデータは以下で表現する。

V^{N}_{M}=\left\{ v_{1},v_{2},\ldots ,v_{N}\right\}

ここで$N$は時間長であり、配列は各時間のデータを示す。時間刻み(サンプリング)は一定である。
Mは列を示す。これは異なるセンサ、もしくは時間軸がズレたデータだと思えばよい。
すなわち、

V^{N}_{1}\in \mathbb{R} ^{M \times N}

が1つのデータ(スナップショット)を表している。

1.1.2. 時間発展

次に、各データの時間発展を考える。

v_{i+1}=Av_i

ここで、$A$は時間発展を表す関数のベクトルである。一般的に非線形かつ未知である。
これは離散力学系であり、連続力学系の場合は時間に関する一階の微分方程式になる。

DMDは、この$A$をデータから推定するEquation freeの方法である。

次に、スナップショットの時間発展を考える。

V^{N}_{2}=AV^{N-1}_{1}+re^{T}_{N-1}

基本的には$A$が時間発展を完璧に表現できるのであれば$N-1$のデータから$N$を推定できるはずである。
しかし、完全に説明できない動作やノイズ等を説明する残差ベクトルも必要なので、$+re^{T}_{N-1}$を付け加える。
ようは、直線の方程式$y=ax+b$の$+b$に近い。

これを分かりやすく時間発展の各要素で表記すると、

$M=1$の場合

V^{N-1}_{1}=\left\{ v_{1},v_{2},\ldots ,v_{N-1}\right\}

$M=2$の場合

V^{N}_{2}=\left\{ v_{2},v_{3},\ldots ,v_{N}\right\}

となる。$M$は時系列$N$が1ずれたデータのスナップショットである。
DMDでは各センサのスナップショット$M$の関係性（相関関係）から時間発展の関数$A$を推定していく。
因みに、直線の方程式からも分かるように、DMDは線型で近似を行う。このため、非線形データの場合は上手く推定できないことがある。

1.1.3. DMDの出力

DMDの出力は$A$の固有値と固有ベクトルである。
それぞれ、DMD固有値、及びDMDモードと呼ばれる。

DMDモードは入力データ(複合的な要素が重ねわさったセンサデータ)をいくつに分解するかということである。

1.2 アルゴリズム

主な計算方法としては、2つありThe Arnoldi法とThe SVD-based法がある。
理論解析的にはThe Arnoldi法が良くて、ノイズや数値誤差が大きいものには特異値分解ベースのSVDが良いといわれている。
よって、数値解析的には特異値分解ベースのSVDを用いる。

1.2.1 The Arnoldi

スパース性を持つ大規模行列を計算するのでクリロフ部分空間法を用いる。

流体のアプリケーションにおいて、スナップショットのサイズ$M$は
スナップショットの数$N$よりも大きいと考えられる。すなわち、センサは長い時間観測していない。
このため、$A$は多くの解を持つこととなる。

ここで、時系列発展させた$V^{N}_{2}$$ は

$V^{N}_{1}$ とDMDによって最適化された線型結合の$A$によって求められる。

各要素の発展系は以下である

v^{N}=a_{1}v_{1}+a_{2}v_{2}\ldots +a_{N-1}v_{N-1}+r=v^{N-1}_{1}a+r

各$a$は重みと考えればよい。

すなわち$V$に関する式にまとめると、

V^{N}_{2}=AV^{N-1}_{1}=V^{N-1}_{1}S+re^{T}_{N-1}

となる。

ここで$S$はコンパニオン行列である。

S=\begin{pmatrix}
0 & 0 & \ldots & 0 & a_{1} \\
1 & 0 & \ldots & 0 & a_{2} \\
0 & 1 & \ldots & 0 & a_{3} \\
\vdots& \vdots&\ddots&\vdots&\vdots&\\
0 & 0 & \ldots & 1 & a_{N-1} \\
\end{pmatrix}

ここで$a$は最小二乗法によって最適化を行い、残差(損失)を最小にする。

$V^{N-1}_1=QR$としたとき、$QR$の分解を行うと、$a=R^{-1}Q^{T}v_{N}$となる。

$S$の固有値は$A$の固有値の近似値といえる。すなわち、
$y$が$S$の固有値とした時、$A=V^{N-1}_{1}y$といえる。厳密には近似の固有ベクトルである。

固有値分解が$S$で行われるのは、$S$が$A$より小さいからである。
DMDの計算コストはスナップショットのサイズ$M$ではなく、スナップショットの数$N$に依存する。

1.2.2 The SVD-based

SVD法によって固有値分解を行う手法について説明する。さしあたり、データの固有値分解と縮約モデル化の2つについて説明する。

1.2.2.1 固有値分解

数値解析によく用いられるSVD法(Singular Value Decomposition: 特異値分解)では、コンパニオン行列$S$は用いない。
代わりに、相似変換(similarity transform)を用いて$A$に関連する$\widetilde {S}$を計算する（$\widetilde {}$は相似を表す）。

まず、フローデータ（時系が進んだデータ）$V_1$及び$V_2$から行列$A$の固有値及び固有ベクトルを求めることを考える。

率直な方法は次式を最小化し、$A$を求めることである。

E=\left\| V_{2}-AV_{1}\right\| ^{2}_{2}

※ここで、$\left|\right| ^{}_{2}$はフロベニウスノルムを表す。

$V_1$の疑似逆行列を$V^{+}_{1}$としたとき、$A$は次式で計算可能である。

A\approx V_{2}V^{+}_{1}

$A$を求めるためには疑似逆行列を求める必要がある。ここでSVD法を用いる。
疑似逆行列$V^{+}_{1}$は特異値分解を用いることで計算できるからである。
$V_1$の特異値分解は次式で表される。

V^{N-1}_1=U\Sigma W^{T}

$U$は特異値分解で得た直行基底である。
これを$V_2$周りで解くと、次式になる。

V^{N}_2=AV^{N-1}_1+re^{T}_{N-1}=AU\Sigma W^{T}+re^{T}_{N-1}

ここで、$W^ T$は$W$の随伴行列を表す。
また、$U$及び$W^T$はそれぞれ、$N×N$、$M×M$の直行行列、$\Sigma$は$N×M$の行列である。
また、行列$V_1$の階数を$r$とすると、$\Sigma$は$r$個の非零の対角成分、すなわち特異値を持つ。

$V^{N}_2$のスナップショットが$U$の列の線形重ね合わせとして表現できるよう$A$を選択(最適化)する。
これはPODモードの重ね合わせとして記述できることと等価である。
残差を最小化するには、それがPOD規定($U^Tr=0$)に直行している必要がある。

以下の式に$U^T$を乗じると、

V^{N}_2=AV^{N-1}_1+re^{T}_{N-1}=AU\Sigma W^{T}+re^{T}_{N-1}

以下の式が求まり、

U^TV^{N}_2=U^TAU\Sigma W^{T}

さらに、これを展開し、$\widetilde {S}$まわりで整理すると以下になる。

U^TAU=U^TV^{N}_2W\Sigma^{-1}\equiv\widetilde {S}

なお、最初の方で示した次式で整理すると

E=\left\| V_{2}-AV_{1}\right\| ^{2}_{2}

以下のようになり、

E=\left\| V_{2}-US\Sigma W^{T}\right\| ^{2}_{2}

これを$S$まわりに整理すると以下となる。

\widetilde{S}\equiv U^TV^{N}_2W\Sigma^{-1}

このとき、$\widetilde{S}$は$r×r$の行列である。多くの場合$r << N$となるため、
$\widetilde{S}$の固有値及び固有ベクトルは容易に求めることが可能である。

なお、$\widetilde{S}$と$A$の関係は相似行列のため、$S$の固有値は$A$の固有値である。
また、$\widetilde{S}$の固有値が$y$の場合、$U_y$が$A$の固有値となる。

1.2.2.2 縮約モデル

簡単のため、$\widetilde{S}$の固有値を

\left\{ \mu_{S_{1}}, \mu_{S_{2}}, \ldots , \mu_{S_{r}}\right\}

対応する固有ベクトルを

\left\{ \phi_{S_{1}}, \phi_{S_{2}}, \ldots , \phi_{S_{r}}\right\}

とする。求めた行列$A$の近似固有値$\mu_j$、固有ベクトル$\phi_j$は、それぞれ以下となる。

\mu_j=\mu_{S_j}

\phi_j=U\phi_{S_j}

固有値$\mu_j$は対応する固有ベクトル$\phi_j$の時間刻み$\Delta t$の間の時間発展を表す。
$\mu_j=e^{\lambda_{j^{\Delta t}}} $から$\lambda_j$の実数部$\sigma_j$及び虚数部$\omega_j$は次式によって求められる。

\sigma_{j}=\dfrac {Real \left\{log \left( \mu_j \right) \right\} }{\Delta t}

\omega_{j}=\dfrac {Imag \left\{log \left( \mu_j \right) \right\} }{\Delta t}

ここで$Real$及び$Imag$は複素数の実数部と虚数部であり、$\sigma_{j}$と$\omega_{j}$は、
それぞれ対応する固有ベクトルの増幅率と振動数を表している。

得られたDMDモードを用いて、入力データを以下のように表現することが可能である。

V\left( x,t\right) =\sum ^{r}_{j=1}a_{j}\phi _{j}\left( x\right)e^{\lambda_{j}t} 

2. 実装手順

SVD法による実装手順について触れる。

A. 時系列データの作成
時系列データ$\mathbb{R} ^{M \times N}$から以下のデータ行列を作成

V^{N-1}_{1}

V^{N}_{2}

B. 特異分解する
$V^{N-1}_{1}$の特異値分解を次式から行い、低ランク近似する。

V^{N-1}_1=U\Sigma W^{T}

C. 時間発展行列を求める
POD基底に射影した時間発展行列を次式から求め、固有値$\mu_j$と固有ベクトル$\phi_j$を求める。

\widetilde{S} \equiv U^TV^{N}_2W\Sigma^{-1}

D. 任意の時間に対する時間発展を求める

V\left( x,t\right) =\sum ^{r}_{j=1}a_{j}\phi _{j}\left( x\right)e^{\lambda_{j}t} 

3. 実装

実際にDMDを用いてモード分解を行う。

3.1. データ作成

まずは、分解する予定の波形データを3つ作り、1つの合成波とする。
プログラムは以下である。

import numpy as np
import matplotlib as mpl
mpl.use('Agg')
import matplotlib.pyplot as plt

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from numpy import dot, multiply, diag, power
from numpy import pi, exp, sin, cos, cosh, tanh, real, imag
from numpy.linalg import inv, eig, pinv
from scipy.linalg import svd, svdvals
from scipy.integrate import odeint, ode, complex_ode
from warnings import warn

# define time and space domains
x = np.linspace(-10, 10, 100) # space
t = np.linspace(0, 6*pi, 80) # time
dt = t[2] - t[1] # sampling period
Xm,Tm = np.meshgrid(x, t)

# create three spatiotemporal patterns
f1 = multiply(20-0.2*power(Xm, 2), exp((2.3j)*Tm))
f2 = multiply(Xm, exp(0.6j*Tm))
f3 = multiply(5*multiply(1/cosh(Xm/2), tanh(Xm/2)), 2*exp((0.1+2.8j)*Tm))

# combine signals and make data matrix
D = (f1 + f2 + f3).T

# create DMD input-output matrices
X = D[:,:-1]
Y = D[:,1:]

ax = []
plt.clf()
ax_count = 1
max_plot_num = 10
indx = 10
fig = plt.figure(figsize=(15, 40))
fig.subplots_adjust(hspace=1)

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('f1_raw')
ax[-1].plot(t, f1.T.real[indx,:], color='blue', label='Real', marker='x')
ax[-1].plot(t, f1.T.imag[indx,:], color='green', label='Complex', marker='x')
ax_count += 1

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('f2_raw')
ax[-1].plot(t, f2.T.real[indx,:], color='blue', label='Real', marker='x')
ax[-1].plot(t, f2.T.imag[indx,:], color='green', label='Complex', marker='x')
ax_count += 1

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('f3_raw')
ax[-1].plot(t, f3.T.real[indx,:], color='blue', label='Real', marker='x')
ax[-1].plot(t, f3.T.imag[indx,:], color='green', label='Complex', marker='x')
ax_count += 1

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('fusion')
ax[-1].plot(t, D.real[indx,:], color='blue', label='Real', marker='x')
ax[-1].plot(t, D.imag[indx,:], color='green', label='Complex', marker='x')
ax_count += 1

plt.savefig( 'output.png' )

exit()

実行すると以下のような画像が生成される。

以下ソースコードの時間方向データが$N$である。
列解像度(空間方向)が100で、行解像度が80である。

x = np.linspace(-10, 10, 100) # space
t = np.linspace(0, 6*pi, 80) # time

これをグリッド分割し、メッシュ化する。

Xm,Tm = np.meshgrid(x, t)

次に、3つの波形を作成する。

f1 = multiply(20-0.2*power(Xm, 2), exp((2.3j)*Tm))
f2 = multiply(Xm, exp(0.6j*Tm))
f3 = multiply(5*multiply(1/cosh(Xm/2), tanh(Xm/2)), 2*exp((0.1+2.8j)*Tm))

XmとTmの掛け算は、ある時刻において各空間の距離が異なる。
ようは波の発生源から100個のセンサが異なる距離に置かれていると考えると分かりやすい(Xm)。
発生源に近いほど高いゲインが発生する。しかし、各センサでゲインは変わるものの周期や減衰率は同じになる。

D = (f1 + f2 + f3).T

次に波形を足し合わせる。

X = D[:,:-1]
Y = D[:,1:]

この複数センサ(100個)によって取得された合成波から$t-1$ずれた$V_1$と$V_2$を作成する。
これから、得られた$X$と$Y$から$f1, f2, f3$を推定していく。

3.2. 特異値分解して固有値、固有ベクトルを求める

plt.savefigの前に以下のコードを入力する。
scipyライブラリのSVDを用いるため、コードが簡潔である。

U2,Sig2,Vh2 = svd(X, False)
ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('SVD')
ax[-1].scatter(range(0, len(Sig2)), Sig2, label="SVD")
ax_count += 1

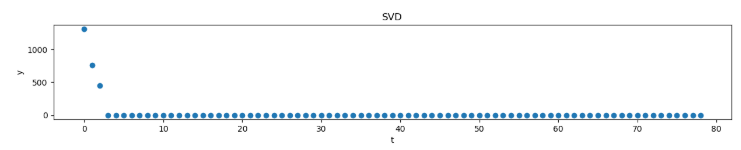
実行すると、以下が求まる

V^{N-1}_1=U\Sigma W^{T}

実行結果は以下である。

これから、特異値（モード）は3つあることが容易に理解できる。
では主成分のみを用い$\widetilde {S}$を計算し、固有値$\mu_j=\mu_{S_j}$及び固有ベクトル$\phi_j=U\phi_{S_j}$を求める。

# rank-3 truncation
r = 3
U = U2[:,:r]
Sig = diag(Sig2)[:r,:r]
V = Vh2.conj().T[:,:r]

# build A tilde
Atil = dot(dot(dot(U.conj().T, Y), V), inv(Sig))
mu,W = eig(Atil)

# build DMD modes
Phi = dot(dot(dot(Y, V), inv(Sig)), W)

3.3. 時間発展させる

以下のコードにより、$r$階(3モード)の時間発展をする。

# compute time evolution
b = dot(pinv(Phi), X[:,0])
Psi = np.zeros([r, len(t)], dtype='complex')
for i,_t in enumerate(t):
    Psi[:,i] = multiply(power(mu, _t/dt), b)

このように元の波形を復元できれば、成功である。

3.4. コードのまとめ

全コードは以下である。

import numpy as np
import matplotlib as mpl
mpl.use('Agg')
import matplotlib.pyplot as plt

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from numpy import dot, multiply, diag, power
from numpy import pi, exp, sin, cos, cosh, tanh, real, imag
from numpy.linalg import inv, eig, pinv
from scipy.linalg import svd, svdvals
from scipy.integrate import odeint, ode, complex_ode
from warnings import warn

# define time and space domains
x = np.linspace(-10, 10, 100) # space
t = np.linspace(0, 6*pi, 80) # time
dt = t[2] - t[1]
Xm,Tm = np.meshgrid(x, t)

# create three spatiotemporal patterns
f1 = multiply(20-0.2*power(Xm, 2), exp((2.3j)*Tm))
f2 = multiply(Xm, exp(0.6j*Tm))
f3 = multiply(5*multiply(1/cosh(Xm/2), tanh(Xm/2)), 2*exp((0.1+2.8j)*Tm))

# combine signals and make data matrix
D = (f1 + f2 + f3).T

# create DMD input-output matrices
X = D[:,:-1]
Y = D[:,1:]

ax = []
plt.clf()
ax_count = 1
max_plot_num = 10
indx = 10
fig = plt.figure(figsize=(15, 40))
fig.subplots_adjust(hspace=1)

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('f1_raw')
ax[-1].plot(t, f1.T.real[indx,:], color='blue', label='Real', marker='x')
ax[-1].plot(t, f1.T.imag[indx,:], color='green', label='Complex', marker='x')
ax_count += 1

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('f2_raw')
ax[-1].plot(t, f2.T.real[indx,:], color='blue', label='Real', marker='x')
ax[-1].plot(t, f2.T.imag[indx,:], color='green', label='Complex', marker='x')
ax_count += 1

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('f3_raw')
ax[-1].plot(t, f3.T.real[indx,:], color='blue', label='Real', marker='x')
ax[-1].plot(t, f3.T.imag[indx,:], color='green', label='Complex', marker='x')
ax_count += 1

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('fusion')
ax[-1].plot(t, D.real[indx,:], color='blue', label='Real', marker='x')
ax[-1].plot(t, D.imag[indx,:], color='green', label='Complex', marker='x')
ax_count += 1


# SVD of input matrix
U2,Sig2,Vh2 = svd(X, False)
ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('SVD')
ax[-1].scatter(range(0, len(Sig2)), Sig2, label="SVD")
ax_count += 1


# rank-3 truncation
r = 3
U = U2[:,:r]
Sig = diag(Sig2)[:r,:r]
V = Vh2.conj().T[:,:r]

# build A tilde
Atil = dot(dot(dot(U.conj().T, Y), V), inv(Sig))
mu,W = eig(Atil)

# build DMD modes
Phi = dot(dot(dot(Y, V), inv(Sig)), W)

# compute time evolution
b = dot(pinv(Phi), X[:,0])
Psi = np.zeros([r, len(t)], dtype='complex')
for i,_t in enumerate(t):
    Psi[:,i] = multiply(power(mu, _t/dt), b)

# compute DMD reconstruction
D2 = dot(Phi, Psi)
np.allclose(D, D2) # True

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('DMD (m1)')
ax[-1].plot(t, Psi.real[0,:], color='blue', label='Original', marker='x')
ax[-1].plot(t, Psi.imag[0,:], color='green', label='Complex', marker='x')
ax_count += 1

ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('DMD (m2)')
ax[-1].plot(t, Psi.real[1,:], color='blue', label='Original', marker='x')
ax[-1].plot(t, Psi.imag[1,:], color='green', label='Complex', marker='x')
ax_count += 1


ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('t')
ax[-1].set_ylabel('y')
ax[-1].set_title('DMD (m3)')
ax[-1].plot(t, Psi.real[2,:], color='blue', label='Original', marker='x')
ax[-1].plot(t, Psi.imag[2,:], color='green', label='Complex', marker='x')
ax_count += 1

plt.savefig( 'output.png' )