2021/7/27 投稿
0. この記事の対象者
- python, sklearnをある程度扱える人
- 次元削減手法q-SNEについて知りたい人
- q-SNEを使ってみたい人
1. はじめに
この記事ではICPR2020で発表された論文「q-SNE: Visualizing Data using q-Gaussian Distributed Stochastic Neighbor Embedding」の解説と実装を行う.
解説は論文の内容を元にしたもので行い,実装は著者のgithubにあるものを使って行う.
2. 論文解説
2-1. 簡潔に言うと
タイトルより「q-SNE: Visualizing Data using q-Gaussian Distributed Stochastic Neighbor Embedding」とあるようにt-SNEがt分布を使っているのに対してq-SNEはqガウス分布というものを使っている.
これによりt−SNEよりも直感的に次元削減後の形を操作できるようになる.
2-2. qガウス分布
qガウス分布はガウス分布の拡張版で,以下のように定義される.
P_q(x;\mu,\sigma^2)=\frac{1}{Z_q}\left( 1+\frac{q-1}{3-1}\frac{(x-\mu)^2}{\sigma^2}\right)^{-\frac{1}{q-1}}\\
Z_q = \begin{cases}
\sqrt{\frac{3-q}{q-1}}Beta\left(\frac{3-q}{2(q-1)},\frac{1}{2}\right)\sigma & 1\leq q<3\\
\sqrt{\frac{3-q}{1-q}}Beta\left(\frac{2-q}{1-q},\frac{1}{2}\right)\sigma & q<1
\end{cases}
上式のようにqガウス分布はハイパーパラメータqを持っており,このqを操作することで次元削減後の埋め込みの形を操作する.
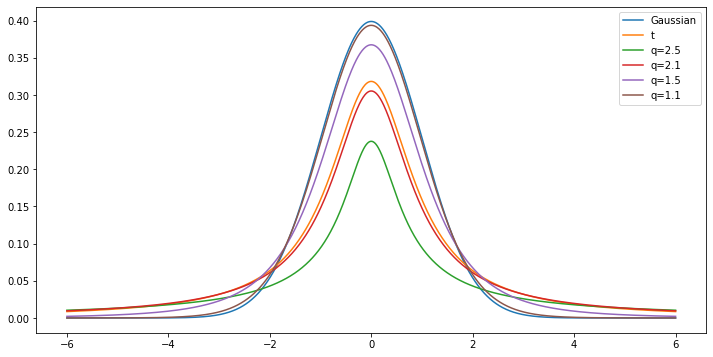
qガウス分布は以下のような確率分布である.
分布から見てわかるように,qが1に近づいていくとガウス分布と一致していき,qが2に近づくとt分布に一致する.
実際にq=1(極限で1)になるとガウス分布,q=2になるとt分布になるようになっている.
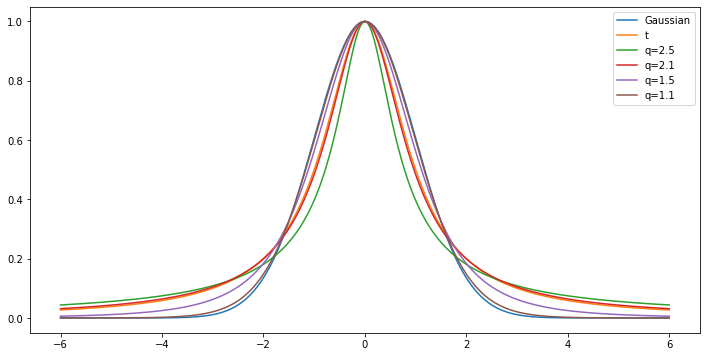
この図は分布の係数部分$Z_q$を含んでいるが,t-SNEないしq-SNEは計算時に係数部分を使用しないため係数を省いた分布もみてみる.
この図を見るとqが大きくなるほど中心が細くなり,裾が大きくなっている.
この分布の変化がわかれば,直感的にqを操作してサンプルの近さを近づけたり離したりできるようになる.
2-3. q-SNEの式
i). 高次元の類似度
SNE系統はこの高次元の類似度を教師無しでいかに評価することがポイントとなっている.
まず,式は以下のようになっている.
p_{j|i}=\frac{\exp{(-\|\boldsymbol{x}_j-\boldsymbol{x}_i\|^2/2\sigma_i^2)}}{\sum_{k\neq i}^N\exp{(-\|\boldsymbol{x}_k-\boldsymbol{x}_i\|^2/2\sigma_i^2)}}
ここで$N$はサンプル数,$\boldsymbol{x}$は$D$次元のサンプルとする.
分子に注目するとサンプル$\boldsymbol{x}_i$というベクトルを平均(中心)としたあるサンプル$\boldsymbol{x}_j$についての多次元ガウス分布となっている.
同様に分母は$\boldsymbol{x}_i$を中心としたガウス分布の全サンプルの総和であることがわかる.
これは$i$番目のサンプルと$j$番目のサンプルは全体的にどれくらい近いよ,というのを測っている.
(ちなみにガウス分布の係数部分は分母分子で打ち消してなくなっている)
ここで多次元ガウス分布の共分散行列をここではスカラーの$\sigma_i$で近似しており,これは以下の式で求める
\log{k}=\sum_{j\neq i}^Np_{j|i}\log{p_{j|i}}
この$k$をperplexityというハイパーパラメータで決め,上式が成り立つような$\sigma$をバイナリーサーチで求める.
これでサンプル$\boldsymbol{x}$周りの類似度を決定し,これを全サンプル分用意する.
しかし,このままでは対象性がなく,$p_{j|i}\neq p_{i|j}$となってしまうので,以下のようにして対称性を作る.
p_{ij} = \frac{1}{2}(p_ip_{j|i}+p_jp_{i|j})=\frac{p_{j|i}+p_{i|j}}{2N}
上の式では$p_i=p_j=\frac{1}{N}$として求まる.
この$p_{ij}$を高次元サンプルの類似度として扱う.
ii). 低次元の類似度
低次元の類似度はqガウス分布を使うと以下のようになる.
r_{ij}=\frac{\left(1+\frac{q-1}{3-q}\|\boldsymbol{y}_j-\boldsymbol{y}_i\|^2\right)^{-\frac{1}{q-1}}}{\sum_l^N\sum_{k\neq l}^N\left(1+\frac{q-1}{3-q}\|\boldsymbol{y}_k-\boldsymbol{y}_l\|^2\right)^{-\frac{1}{q-1}}}
ここで$\boldsymbol{y}$は$d$次元($d<<D$)の次元削減後のベクトルである.
上式のように次元削減後のベクトル間の類似度を高次元のときと同じように測っている.
ここで違う点としては低次元側では分散を1として扱い,分母の総和の際は全サンプル間の類似度の総和を使っている.
(qガウス分布の係数部分は分母分子で打ち消してなくなっている)
ちなみにq=2にすると
r_{ij}=\frac{\left(1+\frac{2-1}{3-2}\|\boldsymbol{y}_j-\boldsymbol{y}_i\|^2\right)^{-\frac{1}{2-1}}}{\sum_l^N\sum_{k\neq l}^N\left(1+\frac{2-1}{3-2}\|\boldsymbol{y}_k-\boldsymbol{y}_l\|^2\right)^{-\frac{1}{2-1}}}=\frac{\left(1+\|\boldsymbol{y}_j-\boldsymbol{y}_i\|^2\right)^{-1}}{\sum_l^N\sum_{k\neq l}^N\left(1+\|\boldsymbol{y}_k-\boldsymbol{y}_l\|^2\right)^{-1}}
となり,完全にt-SNEの式と一致する.
iii). 最適化
高次元の分布に低次元の分布を近づけることで次元削減を行う.
最適化する式は以下の通り.
C=\sum_{i}^N\sum_{j\neq i}^Np_{ij}\log{\frac{p_{ij}}{r_{ij}}}
これはカルバックライブラーダイバージェンスという分布間の近さを評価する損失関数である.
これで$p_{ij}$と$r_{ij}$が近づき,$\boldsymbol{y}$がきれいに可視化されていく.
その$\boldsymbol{y}$の更新式は以下の通り.
\boldsymbol{y}_i^{t+1}=\boldsymbol{y}_i^t-\eta\frac{\partial C}{\partial \boldsymbol{y}_i}+\alpha(t)(\boldsymbol{y}_i^t-\boldsymbol{y}_i^{t-1})\\
\frac{\partial C}{\partial \boldsymbol{y}_i}=\frac{4}{3-q}\sum_j^N(p_{ij}-r_{ij})(\boldsymbol{y}_j-\boldsymbol{y}_i)\left(1+\frac{q-1}{3-q}\|\boldsymbol{y}_j-\boldsymbol{y}_i\|^2\right)^{-1}
ここで$t$はイテレーション,$\eta$は学習率, $\alpha(t)$はモーメンタムを意味する.
3. python実装
実装は上記にも上げたgithubのコードを用いて行う(ここの解説が必要と言われれば追記します).
リポジトリをローカルにcloneし,python環境を整える.
cythonを使用して高速実装をしているため,OSによってcython周りの環境は注意して整える.
(cythonがうまく行かない場合はQSNE.pyの126行目を"_utils._binary_search_perplexity"から"_binary_search_perplexity"に変えれば実行時間は遅くなるが実行できる)
q=2の時の実装プログラムは以下
import numpy as np
from QSNE import QSNE
import matplotlib.pyplot as plt
from sklearn import datasets
digits = datasets.load_digits()
qsne = QSNE(n_components=2, q=2.0, verbose=1)
X_reduced = qsne.fit_transform(digits.data)
target = digits.target
for i in range(10):
plt.scatter(X_reduced[target==i, 0], X_reduced[target==i, 1], label=str(i))
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, ncol=1)
plt.show()
出力結果は以下
qをq=1.1に変えて実装した結果は以下
qを小さくするとqガウス分布の中心周りが太くなるため次元削減したマップも大きく広がっている.
qをq=2.5に変えて実装した結果は以下
qを大きくするとqガウス分布の中心周りが細くなるため次元削減したマップもきゅっと小さくなる.