主成分分析をExcelで理解する

主成分分析（principal component analysis, PCA）とは多変量解析手法のうち次元削減手法としてよく用いられる手法の一種で、相関のある多変数から、相関のない少数で全体のばらつきを最もよく表す変数を合成します。
主成分分析を行う便利なツールとして、Pythonで利用可能なScikit-learnなどがありますが、ここでは、PCAがどのような手法か概観するためにExcelで計算してみたいと思います。

理論的な話は 意味がわかる主成分分析 など詳しい記事がたくさんあります。

ワインのデータ

データは UC Irvine Machine Learning Repository から取得したものを少し改変しました。

https://github.com/maskot1977/ipython_notebook/blob/master/toydata/wine.xlsx

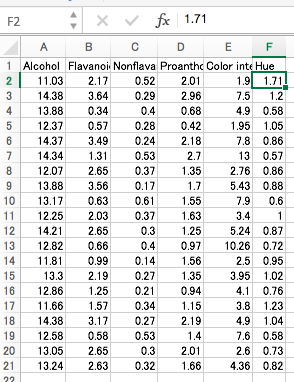
今回のデータは、20個のワインの銘柄の特徴が、６種類の「観測変数」(x₁, x₂, x₃, x₄, x₅, x₆) で表されています。この6変数を説明変数とします。これに対し、PCAで合成する合成変数は「主成分得点」といい、次式のように線型結合で与えられます。「合成変数」と呼んだり「潜在変数」と呼んだりすることもあり、紛らわしいです。

y_PC1 = a_1,1 x₁ + a_1,2 x₂ + a_1,3 x₃ + a_1,4 x₄ + a_1,5 x₅ + a_1,6 x₆
y_PC2 = a_2,1 x₁ + a_2,2 x₂ + a_2,3 x₃ + a_2,4 x₄ + a_2,5 x₅ + a_2,6 x₆
y_PC3 = a_3,1 x₁ + a_3,2 x₂ + a_3,3 x₃ + a_3,4 x₄ + a_3,5 x₅ + a_3,6 x₆
...
y_PC6 = a_6,1 x₁ + a_6,2 x₂ + a_6,3 x₃ + a_6,4 x₄ + a_6,5 x₅ + a_6,6 x₆

ここで、係数 a_ij (i = 1...6, j = 1...6) を「固有ベクトル」といい、主成分得点に対する観測値の影響度を表します。説明変数の個数が p の場合、主成分PCは p 個算出されます。

主成分分析では、固有値（＝主成分得点の分散）が大きい主成分得点ほど重要と判断します。

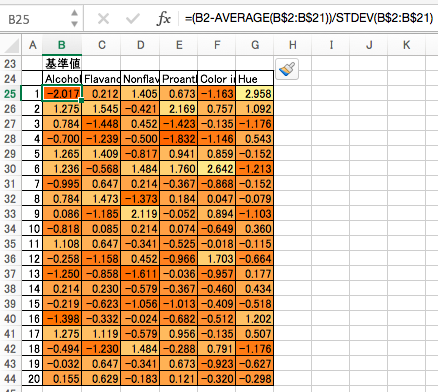
基準値

各列に対して、平均値を引いたものを標準偏差で割ります。

（補足：基準値ではなく、偏差（平均との差）を用いる方法もありますが、偏差を用いる方法は、各列の単位が異なる場合には普通は使いません。ただ、いつでも基準値にすればいいというわけでもないようです。その点については 主成分分析で標準偏差で割るべき？に対する議論 などの解説が詳しいです。）

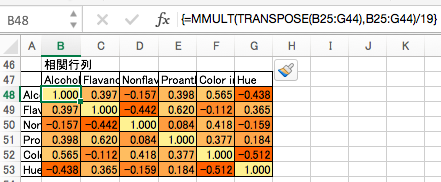
相関行列

基準値の行列に対して、自分自身との行列の積を計算し、データ数 - 1 で割ると相関行列になります。

（補足：偏差を用いる方法では、自分自身との行列の積を計算して データ数 - 1 で割ると「分散共分散行列」と呼ばれる行列になります。）

第1主成分

第1主成分の固有値

相関行列の固有方程式を解きます。相関行列の固有値の第1成分を、主成分分析では「第1主成分(PC1)の固有値」と言います。

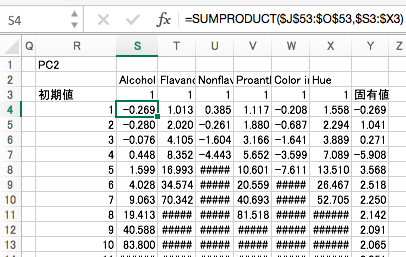
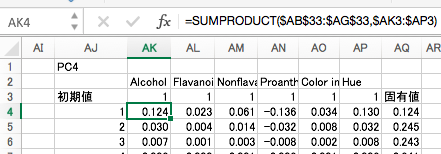
各変数に対する初期値として1を与え、相関行列の第１行目（対称行列なので１列目でも同じ）との線型結合を計算します。

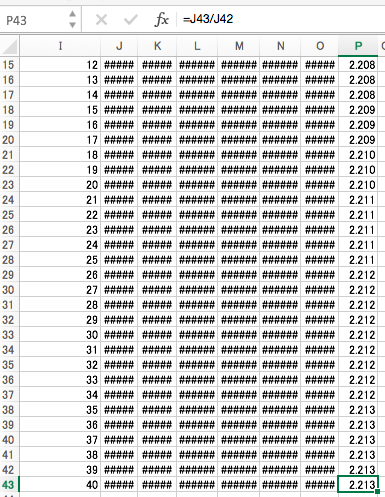
得られた線型結合の１つめ（ここではJ列）の変化量が固有値になります。

以降、このJ4:P4のセルを縦方向に繰り返しコピペして、固有値が落ち着くまで、縦方向の計算を繰り返します。諦めたらそこで計算終了です。

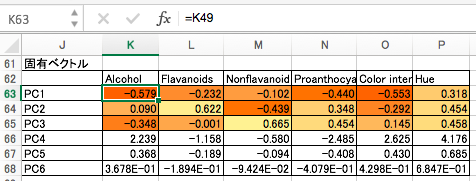
第1主成分の固有ベクトルと主成分負荷量

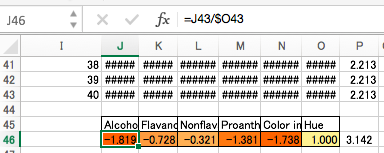
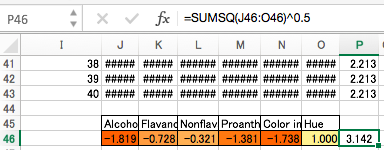
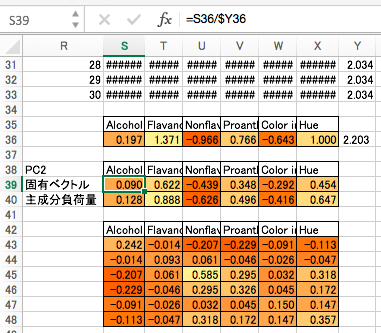
固有値が落ち着いたら、最終的に得られたJ列〜O列の値に対して次のように比率を取り、

２乗和の平方根を取り、

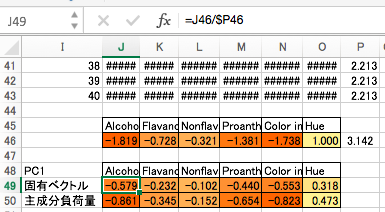
その割合を取れば、主成分分析でいう「第1主成分(PC1)の固有ベクトル」が得られます。このベクトルは相関行列の固有ベクトルの第1列と一致します。

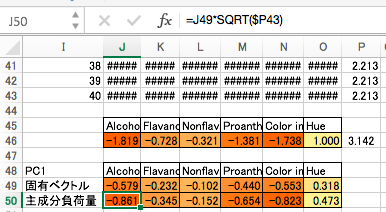
固有ベクトルに、固有値の平方根をかけた値を「主成分負荷量」と言います。

途中結果をチェックしたい

• 相関行列は正方行列で、対称行列で、-1〜1の間の値をとり、対角成分は必ず1です。そうでなければどこかで計算ミスしてます。

• PC1の固有値は、PC1の主成分得点の分散と同じ値になります。固有値の収束の時に多少の計算誤差は出ますが、あまりに誤差が大きい時は、どこかで計算ミスしてると思った方がよいでしょう。（主成分得点の計算方法は、もう少し下にある「主成分得点と固有値」を見てください）

第2主成分

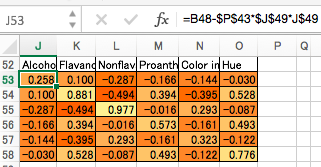
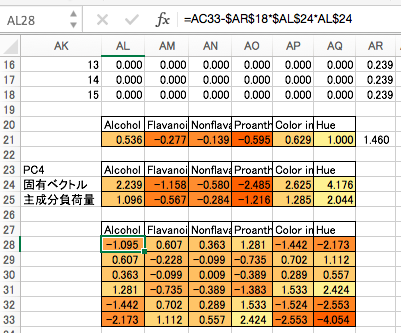
PC1の影響を取り除いた相関行列2（もはや相関行列とは呼べない）を作成します。相関行列と同様、この行列も、各説明変数を行と列にもつ対称行列です。この行列の成分 C'_i,j は、最初の相関行列を C_i,j、固有ベクトルのn番目の成分を V_n とすると、

C'_i,j = C_i,j - PC1の固有値 * V_i * V_j

で計算できます。

相関行列2の固有値の第1成分を、主成分分析では「第2主成分(PC2)の固有値」と言います。相関行列2に対して、PC1の固有値を求めたのと同様の手法で算出します。

同様にして「第2主成分(PC2)の固有ベクトル」を算出します。さらに、PC2の影響を取り除いた相関行列3を作成し、第３主成分の計算に用います。

第3主成分

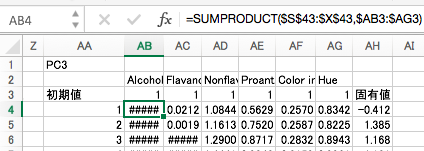
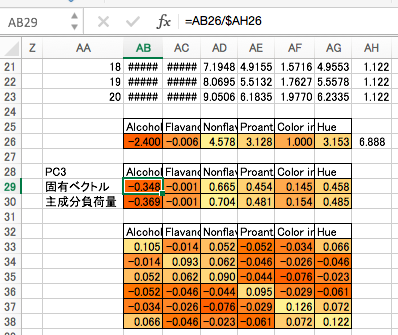
ここから後の流れは第２主成分と同様です。第3主成分の固有値を求めて、第3主成分の固有ベクトルを求めます。そして、第4主成分の計算のために、PC3の影響を取り除いた相関行列4を作成します。

第4主成分

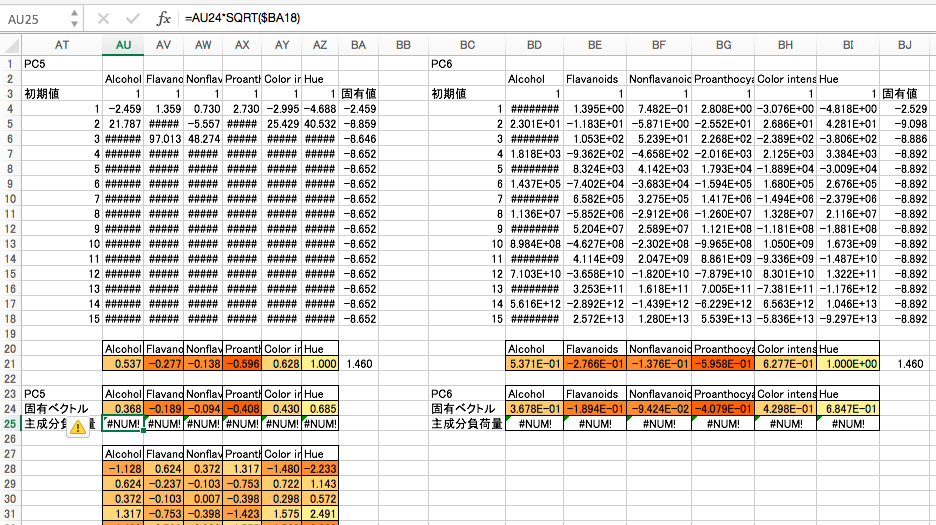
基本的には、これまでと同様の計算を繰り返しますが、経験的に、このあたりから計算がおかしくなってきます。固有値計算の途中経過の絶対値が1.0を下回ると繰り返し計算による収束がおかしくなってきます。

第5主成分・第6主成分

計算がおかしくなってきたのは承知の上ですが、諦めず最後まで計算してみましょう。

主成分得点と固有値

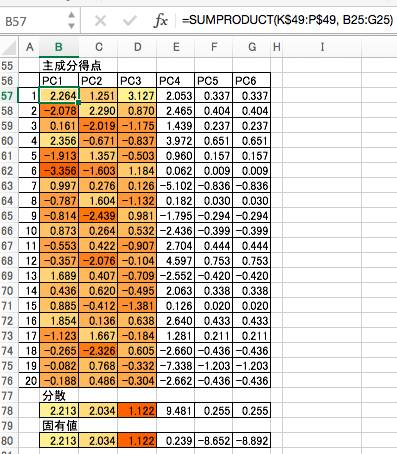
主成分得点は、主成分の固有ベクトルと説明変数との線型結合で計算できます。本来は、主成分得点の分散と、主成分の固有値は等しくなるはずなのですが、固有値の収束がおかしいとこの２つの値が異なってきます。今回の例では、PC3までは大丈夫そうですが、PC4以降は信用できません。

また、今回は「PC4以降は信用できない」という結果になってしまいましたが、Pythonのscikit-learnなど、主成分分析を実行する専用の計算ライブラリを使用すると最後まで計算できます。そのときには、各主成分の固有値（＝分散）の和をとり、その和の中で各固有値が何割を占めているかを「寄与度」とみなして、寄与度の大きい主成分ほど重要であるとします。（今回は寄与度の計算ができません）

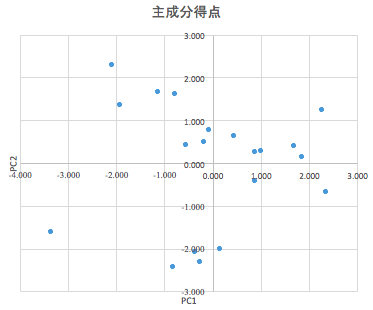
主成分得点を用いて各サンプル（ワインの銘柄）をプロットしてみましょう。

この横軸(PC1)、縦軸(PC2)にいかほどの意味が解釈できるかは、次の固有ベクトルに依存します。

固有ベクトル

主成分得点と同様、今回はPC4以降の固有ベクトルの計算結果は信用できません。

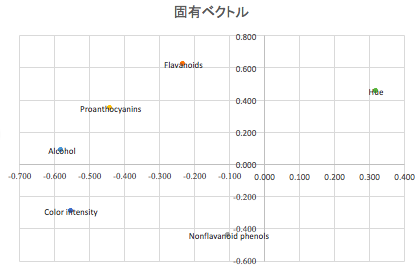
固有ベクトルを用いて各説明変数をプロットしてみましょう。

横軸(PC1）は、Hueを正に強く評価し、AlcoholやColor intensityを負に強く評価したような指標です。縦軸(PC2)はFlavonoidsを正に強く評価し、Nonflavonoid phenolsを負に強く評価したような指標です。こうしたプロットを見ることで、各変数の相互の関係が概観できます。

また、主成分得点のプロットと固有ベクトルのプロットを合わせて考えることで、各サンプルの主成分点に基づいた解釈の助けになります。

追記：第4主成分以降の固有値の収束について訂正

本記事では、経験的に第4主成分以降は固有値と主成分の分散が一致しないので信用できないという旨の記載をしましたが、もっと頑張って２００回くらい繰り返し計算をすれば収束するとの報告をいただきました。私は４０回くらいで諦めてしまいましたが、諦めたらそこで試合終了でした。報告してくれた学生さん、ありがとうございました！

課題

• 第１主成分 vs 第２主成分、第１主成分 vs 第３主成分、第２主成分 vs 第３主成分で主成分得点のプロット、固有ベクトルのプロットを作成し、その結果について考察してください。

• 実習用データ から「都道府県別アルコール類の消費量」を取得し、同様に主成分分析を行い、その結果について考察してください。また、基準値を用いる方法と、偏差を用いる方法の結果を比較してください。