Scipyで実装しながら学ぶ ロジスティック回帰 と 多層パーセプトロン の基礎

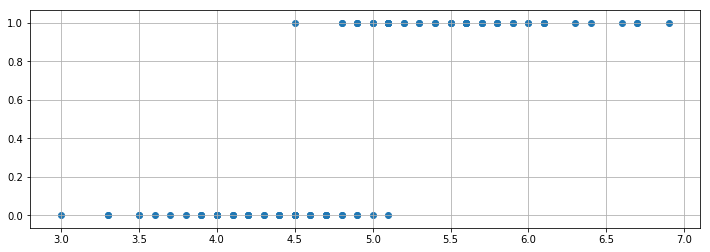
補間やカーブフィッティングなどの最適化 では、様々な曲線に近似する方法を学びました。それでは、次のように、$Y$ が $０$ か $１$ しかない場合にはどんな曲線に近似すれば良いでしょうか？

X1 = [4.7, 4.5, 4.9, 4.0, 4.6, 4.5, 4.7, 3.3, 4.6, 3.9, 
      3.5, 4.2, 4.0, 4.7, 3.6, 4.4, 4.5, 4.1, 4.5, 3.9, 
      4.8, 4.0, 4.9, 4.7, 4.3, 4.4, 4.8, 5.0, 4.5, 3.5, 
      3.8, 3.7, 3.9, 5.1, 4.5, 4.5, 4.7, 4.4, 4.1, 4.0, 
      4.4, 4.6, 4.0, 3.3, 4.2, 4.2, 4.2, 4.3, 3.0, 4.1, 
      6.0, 5.1, 5.9, 5.6, 5.8, 6.6, 4.5, 6.3, 5.8, 6.1, 
      5.1, 5.3, 5.5, 5.0, 5.1, 5.3, 5.5, 6.7, 6.9, 5.0, 
      5.7, 4.9, 6.7, 4.9, 5.7, 6.0, 4.8, 4.9, 5.6, 5.8, 
      6.1, 6.4, 5.6, 5.1, 5.6, 6.1, 5.6, 5.5, 4.8, 5.4, 
      5.6, 5.1, 5.1, 5.9, 5.7, 5.2, 5.0, 5.2, 5.4, 5.1]

Y = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
     0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
     0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
     0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
     0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1]

とりあえずデータを図示してみましょう。

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(12,4))
plt.scatter(X1, Y)
plt.grid()
plt.show()

ロジスティック回帰

このような関係を近似するときに、シグモイド曲線に近似する「ロジスティック回帰」（Logistic Regression）を使います。scipy.optimize.curve_fit で実装してみましょう。

# Python の List を Numpy の Array に変換しておきましょう。
import numpy as np
X1 = np.array(X1)
Y = np.array(Y)

説明変数が１つのシグモイド曲線に近似

説明変数が１つのシグモイド曲線 func1 を定義します。 $a$ と $b$ を最適化することになります。

import numpy as np
def func1(X, a, b): # シグモイド曲線
    f = a + b * X
    return 1. / (1. + np.exp(-f))

func1 の使用例はこんな感じ。

func1(X1, 1, 1)

array([0.99666519, 0.99592986, 0.99726804, 0.99330715, 0.99631576,
       0.99592986, 0.99666519, 0.98661308, 0.99631576, 0.99260846,
       0.98901306, 0.9945137 , 0.99330715, 0.99666519, 0.9900482 ,
       0.99550373, 0.99592986, 0.9939402 , 0.99592986, 0.99260846,
       0.99698158, 0.99330715, 0.99726804, 0.99666519, 0.9950332 ,
       0.99550373, 0.99698158, 0.99752738, 0.99592986, 0.98901306,
       0.99183743, 0.9909867 , 0.99260846, 0.99776215, 0.99592986,
       0.99592986, 0.99666519, 0.99550373, 0.9939402 , 0.99330715,
       0.99550373, 0.99631576, 0.99330715, 0.98661308, 0.9945137 ,
       0.9945137 , 0.9945137 , 0.9950332 , 0.98201379, 0.9939402 ,
       0.99908895, 0.99776215, 0.99899323, 0.99864148, 0.99888746,
       0.9994998 , 0.99592986, 0.99932492, 0.99888746, 0.99917558,
       0.99776215, 0.99816706, 0.99849882, 0.99752738, 0.99776215,
       0.99816706, 0.99849882, 0.99954738, 0.99962939, 0.99752738,
       0.9987706 , 0.99726804, 0.99954738, 0.99726804, 0.9987706 ,
       0.99908895, 0.99698158, 0.99726804, 0.99864148, 0.99888746,
       0.99917558, 0.99938912, 0.99864148, 0.99776215, 0.99864148,
       0.99917558, 0.99864148, 0.99849882, 0.99698158, 0.9983412 ,
       0.99864148, 0.99776215, 0.99776215, 0.99899323, 0.9987706 ,
       0.99797468, 0.99752738, 0.99797468, 0.9983412 , 0.99776215])

scipy.optimize.curve_fit を使って、 $a$ と $b$ の最適解を得ます。

from scipy.optimize import curve_fit  
popt, pcov = curve_fit(func1,X1,Y) # poptは最適推定値、pcovは共分散
popt

array([-47.16056308,   9.69474387])

これが $a$ と $b$ の最適解になります。

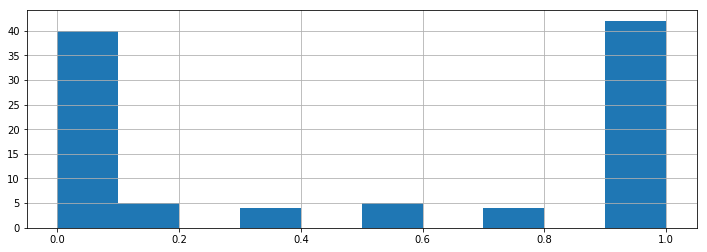
得られた最適解を用いて $X_1$ をシグモイド曲線に回帰すると、その予測された $Y$ の値は、「０か１のどちらに分類されるか予測するとき、１への分類が正しいとされる確率」と解釈できます。その確率の分布を見てみましょう。

plt.figure(figsize=(12,4))
plt.hist(func1(X1, -47.16056308,   9.69474387))
plt.grid()
plt.show()

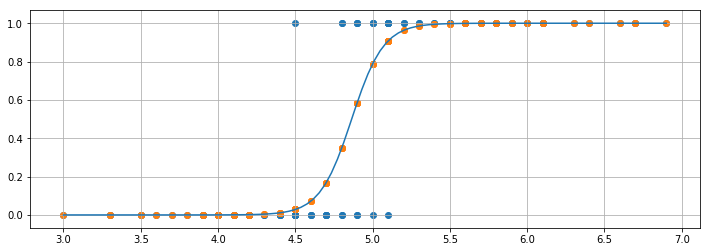
得られた最適解を用いて $X_1$ をシグモイド曲線に回帰すると、下のような図になります。青いドットが元データ、曲線が回帰曲線、オレンジのドットが回帰後のデータになります。この縦軸が、「 $０$ か $１$ のどちらに分類されるか予測するとき、$１$ への分類が正しいとされる確率」です。

課題1

matplotlib を使って、上図のような回帰曲線を図示しなさい。

予測精度の見積もり

実際の分類（ $０$ か $１$ か）は $Y$ という変数に入っています。回帰して得られた値が $0.5$ 以上のときは $１$、 $0.5$ 未満の時は $０$ に分類するなど、閾値を設定した場合、それがどのくらい正確かを計算できます。ここで、

• TP （True Positives, 真の陽性）： $１$ と予想したものが本当に $１$ だった
• FP （False Positives, 偽陽性）： $１$ と予想したものが実は $０$ だった
• FN （False Negatives, 偽陰性）： $０$ と予想したものが実は $１$ だった
• TN （True Negatives, 真の陰性）： $０$ と予想したものが本当に $０$ だった

とします。

課題2

評価指標はいろいろあります。ここでは最も単純な

Accuracy （正答率） = (TP + TN) / (TP + FP + FN + TN) を計算しなさい。

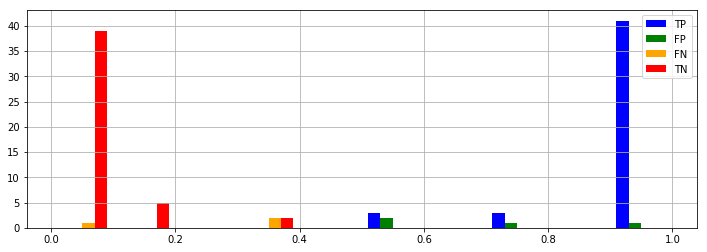
また、下図のように、TP, FP, FN, TN ごとの確率分布を図示しなさい。

print("Accuracy: ", len(TP + TN) / len(TP + FP + FN + TN))
plt.figure(figsize=(12,4))
plt.hist([TP, FP, FN, TN], label=['TP', 'FP', 'FN', 'TN'], color=['blue', 'green', 'orange', 'red'])
plt.legend()
plt.grid()
plt.show()

説明変数が２つのシグモイド曲線に近似

説明変数が２つの場合を試してみましょう。

X2 = [1.4, 1.5, 1.5, 1.3, 1.5, 1.3, 1.6, 1.0, 1.3, 1.4, 
      1.0, 1.5, 1.0, 1.4, 1.3, 1.4, 1.5, 1.0, 1.5, 1.1, 
      1.8, 1.3, 1.5, 1.2, 1.3, 1.4, 1.4, 1.7, 1.5, 1.0, 
      1.1, 1.0, 1.2, 1.6, 1.5, 1.6, 1.5, 1.3, 1.3, 1.3, 
      1.2, 1.4, 1.2, 1.0, 1.3, 1.2, 1.3, 1.3, 1.1, 1.3, 
      2.5, 1.9, 2.1, 1.8, 2.2, 2.1, 1.7, 1.8, 1.8, 2.5, 
      2.0, 1.9, 2.1, 2.0, 2.4, 2.3, 1.8, 2.2, 2.3, 1.5, 
      2.3, 2.0, 2.0, 1.8, 2.1, 1.8, 1.8, 1.8, 2.1, 1.6, 
      1.9, 2.0, 2.2, 1.5, 1.4, 2.3, 2.4, 1.8, 1.8, 2.1, 
      2.4, 2.3, 1.9, 2.3, 2.5, 2.3, 1.9, 2.0, 2.3, 1.8]

X = np.array([X1, X2])

説明変数が２つのシグモイド曲線 func2 を定義します。 $a$ （定数項）と $b$ （X1の係数）と $c$ （X2の係数）を最適化することになります。

課題3

• func2 を定義し、係数 $a$ と $b$ と $c$ の最適解を scipy.optimize.curve_fit を使って得なさい。
• 課題２と同様に、正答率を計算しなさい。
• 課題２と同様に、TP, FP, FN, TN ごとの確率分布を図示しなさい。
• 説明変数が１つの場合と比較して、正答率がどうなったか答えなさい。

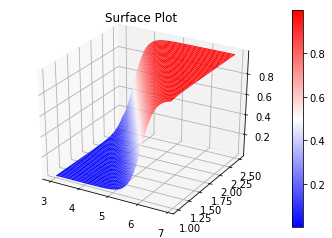
回帰曲面の図示

説明変数が２つありますので、回帰「曲線」ではなく回帰「曲面」になります。 matplotlib で3Dプロット を参考に図示してみましょう。

N = 1000
x1_axis = np.linspace(min(X[0]), max(X[0]), N)
x2_axis = np.linspace(min(X[1]), max(X[1]), N)
x1_grid, x2_grid = np.meshgrid(x1_axis, x2_axis)
x_mesh = np.c_[np.ravel(x1_grid), np.ravel(x2_grid)]

得られた $a$ と $b$ と $c$ が次の値であったとして、

y_plot = func2(x_mesh.T, -34.73855674,   4.53539756,   7.68378862).reshape(x1_grid.shape)

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(x1_grid, x2_grid, y_plot, cmap='bwr', linewidth=0)
fig.colorbar(surf)
ax.set_title("Surface Plot")
fig.show()

ここで大事なことは、シグモイド曲線（あるいは曲面）に回帰していますが、分類問題として考えると、分類境界は「直線」（あるいは平面）であるということです。

より多変数のシグモイド曲線に近似

より多くの説明変数に対応できるように改良しましょう。

X3 = [7.0, 6.4, 6.9, 5.5, 6.5, 5.7, 6.3, 4.9, 6.6, 5.2, 
      5.0, 5.9, 6.0, 6.1, 5.6, 6.7, 5.6, 5.8, 6.2, 5.6, 
      5.9, 6.1, 6.3, 6.1, 6.4, 6.6, 6.8, 6.7, 6.0, 5.7, 
      5.5, 5.5, 5.8, 6.0, 5.4, 6.0, 6.7, 6.3, 5.6, 5.5, 
      5.5, 6.1, 5.8, 5.0, 5.6, 5.7, 5.7, 6.2, 5.1, 5.7, 
      6.3, 5.8, 7.1, 6.3, 6.5, 7.6, 4.9, 7.3, 6.7, 7.2, 
      6.5, 6.4, 6.8, 5.7, 5.8, 6.4, 6.5, 7.7, 7.7, 6.0, 
      6.9, 5.6, 7.7, 6.3, 6.7, 7.2, 6.2, 6.1, 6.4, 7.2, 
      7.4, 7.9, 6.4, 6.3, 6.1, 7.7, 6.3, 6.4, 6.0, 6.9, 
      6.7, 6.9, 5.8, 6.8, 6.7, 6.7, 6.3, 6.5, 6.2, 5.9]

X4 = [3.2, 3.2, 3.1, 2.3, 2.8, 2.8, 3.3, 2.4, 2.9, 2.7, 
      2.0, 3.0, 2.2, 2.9, 2.9, 3.1, 3.0, 2.7, 2.2, 2.5, 
      3.2, 2.8, 2.5, 2.8, 2.9, 3.0, 2.8, 3.0, 2.9, 2.6, 
      2.4, 2.4, 2.7, 2.7, 3.0, 3.4, 3.1, 2.3, 3.0, 2.5, 
      2.6, 3.0, 2.6, 2.3, 2.7, 3.0, 2.9, 2.9, 2.5, 2.8, 
      3.3, 2.7, 3.0, 2.9, 3.0, 3.0, 2.5, 2.9, 2.5, 3.6, 
      3.2, 2.7, 3.0, 2.5, 2.8, 3.2, 3.0, 3.8, 2.6, 2.2, 
      3.2, 2.8, 2.8, 2.7, 3.3, 3.2, 2.8, 3.0, 2.8, 3.0, 
      2.8, 3.8, 2.8, 2.8, 2.6, 3.0, 3.4, 3.1, 3.0, 3.1, 
      3.1, 3.1, 2.7, 3.2, 3.3, 3.0, 2.5, 3.0, 3.4, 3.0]

X = np.array([X1, X2, X3, X4])

任意の数の説明変数に対応できるよう関数を改良します。

import numpy as np
def func(X, *params):
    f = np.zeros_like(X[0])
    for i, param in enumerate(params):
        if i == 0:
            f = f + param
        else:
            f = f + np.array(param * X[i - 1])
    return 1. / (1. + np.exp(-f))

課題4

補間やカーブフィッティングなどの最適化 を参考に、

• func を用いて、最初の１変数 $X_1$ だけを用いた予測を行い、正答率を計算しなさい。
• func を用いて、最初の2変数 $X_1$, $X_2$ だけを用いた予測を行い、正答率を計算しなさい。
• func を用いて、最初の3変数 $X_1$, $X_2$, $X_3$ だけを用いた予測を行い、正答率を計算しなさい。
• func を用いて、4変数 $X_1$, $X_2$, $X_3$, $X_4$ 全てを用いた予測を行い、正答率を計算しなさい。

課題４ 補足

func1 では、x1 だけを用いて y を予測します。
func2 では、x1 と x2 を用いて y を予測します。

同様に

func3 では、x1 と x2 と x3 を用いて y を予測します。
func4 では、x1 と x2 と x3 と x4 を用いて y を予測します。

というふうにしても良いのかもしれませんが、説明変数の数が増えるたびに新しい関数を用意するのでは生産性が低いので、

func で x1 だけを用いて y を予測します。
func で x1 と x2 を用いて y を予測します。
func で x1 と x2 と x3 を用いて y を予測します。
func で x1 と x2 と x3 と x4 を用いて y を予測します。
func で x1, x2, ..., x10 を用いて y を予測します。

というふうに、説明変数の数が増えても対応できるような、汎用性の高い func を開発しましょう、という意図です。

scikit-learn のススメ

以上のような計算を「ロジスティック回帰」と呼びます。ロジスティック回帰は、機械学習における「分類」手法の１つとして使われます。今回はロジスティック回帰の理解と scipy.optimize.curve_fit の使用方法の理解を目的としましたが、実用的には scikit-learn という機械学習ライブラリを用いた計算が便利です。

多層パーセプトロン

多層パーセプトロン（Multilayer perceptron、MLP）は、順伝播型ニューラルネットワークの一種であり、少なくとも3つのノードの層（入力層 X、隠れ層 H、出力層 O）からなります。入力ノード以外の個々のノードは非線形活性化関数を使用するニューロンであり、誤差逆伝播法（バックプロパゲーション）と呼ばれる教師あり学習手法を利用することで、線形分離可能ではないデータを識別できます。非線形活性化関数として使われる関数のひとつに、シグモイド関数があります。

今回はMLPを次のように scipy.optimize.curve_fit で実装しようと思います。

def mlp(X, *params):
    h01, h02, h03, h04, h0b = params[0], params[1], params[2], params[3], params[4]
    h11, h12, h13, h14, h1b = params[5], params[6], params[7], params[8], params[9]
    h21, h22, h23, h24, h2b = params[10], params[11], params[12], params[13], params[14]

    o01, o02, o03, o0b = params[15], params[16], params[17], params[18]

    h0 = 1. / (1. + np.exp(-(h01 * X[0] + h02 * X[1] + h03 * X[2] + h04 * X[3] + h0b)))
    h1 = 1. / (1. + np.exp(-(h11 * X[0] + h12 * X[1] + h13 * X[2] + h14 * X[3] + h1b)))
    h2 = 1. / (1. + np.exp(-(h21 * X[0] + h22 * X[1] + h23 * X[2] + h24 * X[3] + h2b)))

    o0 = 1. / (1. + np.exp(-(o01 * h0 + o02 * h1 + o03 * h2 + o0b)))

    return o0

課題5

• 上記の mlp はどのような構成か説明せよ。
• mlp を用いて、4変数 $X_1$, $X_2$, $X_3$, $X_4$ 全てを用いた予測を行い、正答率を計算しなさい。

課題５ 補足

MLP は初期値依存性が高く、初期値によっては期待通りの動作をしないことがあります。思ったような挙動を示さないなと思ったら、初期値を少し変えてみてください。

scikit-learn と pytorch

MLPは、ディープラーニング（深層学習）と呼ばれる機械学習法のうち、最も簡単な構成をもつものです。今回は MLP の理解と scipy.optimize.curve_fit の使用方法の理解を目的としましたが、実用的には scikit-learn や pytorch などのライブラリを用いた計算が便利です。

参考記事：線形重回帰からロジスティック回帰、多層パーセプトロン、オートエンコーダーまでPyTorchでいっぱい統治する

• https://qiita.com/maskot1977/items/2fb459c66d49ba550db2