線形重回帰からロジスティック回帰、多層パーセプトロン、オートエンコーダーまでPyTorchでいっぱい統治する

PyTorch を使って、深層学習（deep learning）の基本的な考えを学びます。

PyTorch の基本パーツ

次のように、 numpy の array 型で表されたデータがあるとしましょう。

import numpy as np
x1 = np.array([0.12, 0.21])
x2 = np.array([0.34, 0.43])
x3 = np.array([0.56, 0.65])

次のようにして線型結合できます。

z = 0.5 * x1 + 0.3 * x2 + 0.2 * x3
z

array([0.274, 0.364])

Pytorch では、numpy の array を tensor 型に変換して使用します。

import torch
x1 = torch.from_numpy(x1).float()
x2 = torch.from_numpy(x2).float()
x3 = torch.from_numpy(x3).float()

同じように線型結合できます。

z = 0.5 * x1 + 0.3 * x2 + 0.2 * x3
z

tensor([0.2740, 0.3640])

めんどくさいように見えますが、tensor型をさらにVariable型に変換することで、自動的に微分できる（勾配を算出できる）ようになります。

from torch.autograd import Variable
x1 = Variable(x1)
x2 = Variable(x2)
x3 = Variable(x3)

同じように線型結合できます。

z = 0.5 * x1 + 0.3 * x2 + 0.2 * x3
z

tensor([0.2740, 0.3640])

Pytoach では、線型結合する関数が用意してあります。その前に、線型結合を numpy で表現してみましょう。

import numpy as np
W = np.array([[ 5,  1, -2 ],
       [ 3,  -5, -1 ]], dtype=np.float32) # 重み行列 

b = np.array([2, -3], dtype=np.float32) # バイアス項

次のようにして線型結合できます。

x = np.array([0, 1, 2]) # ３変数から成るデータが１レコード
y = x.dot(W.T) + b
y

array([ -1., -10.])

３変数から成るデータが５レコードの場合は次のようになります。

x = np.array(range(15)).astype(np.float32).reshape(5, 3)
x

array([[ 0.,  1.,  2.],
       [ 3.,  4.,  5.],
       [ 6.,  7.,  8.],
       [ 9., 10., 11.],
       [12., 13., 14.]], dtype=float32)

y = x.dot(W.T) + b
y

array([[ -1., -10.],
       [ 11., -19.],
       [ 23., -28.],
       [ 35., -37.],
       [ 47., -46.]], dtype=float32)

以上が、numpy を用いた線型結合です。Pytorchでは、線型結合を表す関数は次のように定義されます。

h = torch.nn.Linear(3,2) # 3次元ベクトルを入力し、2次元のベクトルを出力する線形作用関数 y = Wx + b

デフォルトでは重み行列 W とバイアス項 b には乱数が入ります。これらの係数を最適化するのが、深層学習の目的です。

h.weight # デフォルトでは乱数が入る

Parameter containing:
tensor([[-0.2569, -0.5403,  0.4155],
        [-0.5554,  0.5284,  0.3978]], requires_grad=True)

h.bias # デフォルトでは乱数が入る

Parameter containing:
tensor([-0.5164, -0.2875], requires_grad=True)

ちなみに、tensor型のデータをnumpyのarray型に変換するには次のようにします。

h.weight.detach().numpy()

array([[-0.256898  , -0.54026437,  0.41552007],
       [-0.55537015,  0.5283861 ,  0.39781755]], dtype=float32)

h.bias.detach().numpy()

array([-0.5163672 , -0.28754294], dtype=float32)

では、 Pytorchを用いて線形変換してみましょう。

x = Variable(torch.from_numpy(x).float()) # array型→tensor型→Variable型に変換

y = h(x) # 線形変換

y.data.detach().numpy() # 得られた値をarray型で確認

array([[-0.22559142,  1.0364783 ],
       [-1.3705183 ,  2.1489787 ],
       [-2.515445  ,  3.2614794 ],
       [-3.660372  ,  4.37398   ],
       [-4.805299  ,  5.48648   ]], dtype=float32)

x = x.detach().numpy()
x.dot(h.weight.detach().numpy().T) + h.bias.detach().numpy() # 検算

array([[-0.22559142,  1.0364783 ],
       [-1.3705183 ,  2.1489787 ],
       [-2.515445  ,  3.2614794 ],
       [-3.660372  ,  4.37398   ],
       [-4.805299  ,  5.48648   ]], dtype=float32)

アヤメのデータ

それでは、Pytorch の練習として、線形重回帰をしてみましょう。取り扱うデータとして、機械学習分野でよく用いられる Iris （アヤメ）のデータを取り扱います。

import numpy as np
from sklearn import datasets
iris = datasets.load_iris() # アヤメのデータの読み込み
data = iris.data.astype(np.float32)
X = data[:, :3] # アヤメの計測データのうち、最初の３つを説明変数とします。
Y = data[:, 3].reshape(len(data), 1) # 最後の１つを目的変数とします。

# 奇数番目のデータを教師データ、偶数番目のデータをテストデータとします。
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :] # 説明変数（教師データ）
X_test = X[index[index % 2 == 0], :] # 説明変数（テストデータ）
Y_train = Y[index[index % 2 != 0], :] # 目的変数（教師データ）
Y_test = Y[index[index % 2 == 0], :] # 目的変数（テストデータ）

データをtensor型で表現します。

import torch
X_train = torch.from_numpy(X_train).float()
X_test = torch.from_numpy(X_test).float()
Y_train = torch.from_numpy(Y_train).float()
Y_test = torch.from_numpy(Y_test).float()

X_train.shape

torch.Size([75, 3])

説明変数と目的変数をまとめて TensorDataset 型のデータにします。

from torch.utils.data import TensorDataset
train = TensorDataset(X_train, Y_train)

train[0]

(tensor([4.9000, 3.0000, 1.4000]), tensor([0.2000]))

深層学習では、教師データを小さい「バッチ」に分割して学習します。

from torch.utils.data import DataLoader
train_loader = DataLoader(train, batch_size=10, shuffle=True)

線形重回帰 Multiple Linear Regresion (MLR)

線形重回帰を行うクラスを定義します。

class MLR(torch.nn.Module):
    def __init__(self, n_input, n_output):
        super(MLR, self).__init__()
        self.l1 = torch.nn.Linear(n_input, n_output)

    def forward(self, x):
        return self.l1(x)

そのクラスのオブジェクトを生成します。

model = MLR(3, 1) # 入力が３変数、出力が１変数の線形重回帰モデル

誤差（深層学習では「損失」という）を最小化するのが目的ですが、その誤差を定義します。

criterion = torch.nn.MSELoss() # mean square error

誤差を最小化するアルゴリズムを選択します。

optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 確率的勾配降下法

順方向の計算で「予測」し、誤差を算出した後、誤差を逆方向に伝播する操作を繰り返します。

from torch.autograd import Variable
loss_history = []
for epoch in range(100):
    total_loss = 0
    for x_train, y_train in train_loader:
        x_train = Variable(x_train)
        y_train = Variable(y_train)
        optimizer.zero_grad()
        y_pred = model(x_train)
        loss = criterion(y_pred, y_train)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    loss_history.append(total_loss)
    if (epoch +1) % 10 == 0:
        print(epoch + 1, total_loss)

10 0.5098993554711342
20 0.49431246891617775
30 0.37891835160553455
40 0.38362359534949064
50 0.602457270026207
60 0.4444280909374356
70 0.41419393196702003
80 0.4345690496265888
90 0.38460623472929
100 0.3826814219355583

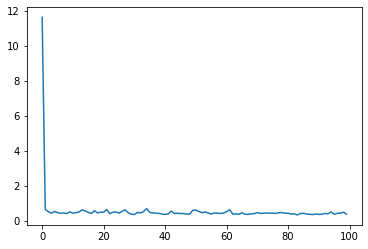
誤差（損失）が減少していくのを確認できたでしょうか？
履歴を図示してみましょう。

%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)

[<matplotlib.lines.Line2D at 0x7fc33444d128>]

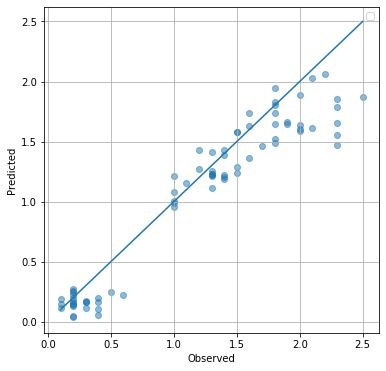
では、予測値と実測値を比較した y-y プロットを眺めてみましょう。対角線に近いほど、良い予測だと言えます。

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
plt.scatter(Y_train.flatten(), model.forward(X_train).data.flatten(), alpha=0.5)
plt.plot([min(Y), max(Y)], [min(Y), max(Y)])
plt.grid()
plt.legend()
plt.xlabel('Observed')
plt.ylabel('Predicted')
plt.show()

ロジスティック回帰 Logistic Regression (LR)

次は、シグモイド関数（ロジスティック関数）に回帰する手法であり、分類手法としても用いられるロジスティック回帰を行ってみましょう。

アヤメのデータ

今度は、アヤメの４つの計測データを説明変数に、アヤメの品種（３種）を目的変数にします。

import numpy as np
from sklearn import datasets
iris = datasets.load_iris() # アヤメのデータの読み込み
X = iris.data.astype(np.float32) # ４変数を説明変数に
Y = iris.target # アヤメの品種（３種）を目的変数に

# アヤメの品種を one-hot vector に変換します。
Y_ohv = np.zeros(3 * Y.size).reshape(Y.size, 3).astype(np.float32)
for i in range(Y.size):
    Y_ohv[i, Y[i]] = 1.0 # one-hot vector

# 奇数番目のデータを教師データ、偶数番目のデータをテストデータとします。
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :] # 説明変数（教師データ）
X_test = X[index[index % 2 == 0], :] # 説明変数（テストデータ）
Y_train = Y_ohv[index[index % 2 != 0], :] # 目的変数の one-hot vector （教師データ）
Y_test = Y_ohv[index[index % 2 == 0], :] # 目的変数の one-hot vector （テストデータ）
Y_ans_train = Y[index[index % 2 != 0]] # 目的変数（教師データ）
Y_ans_test = Y[index[index % 2 == 0]] # 目的変数（テストデータ）

import torch
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader

X_train = torch.from_numpy(X_train).float()
X_test = torch.from_numpy(X_test).float()
Y_train = torch.from_numpy(Y_train).float()
Y_test = torch.from_numpy(Y_test).float()

train = TensorDataset(X_train, Y_train)

train_loader = DataLoader(train, batch_size=10, shuffle=True)

train[0]

(tensor([4.9000, 3.0000, 1.4000, 0.2000]), tensor([1., 0., 0.]))

#import torch.nn.functional as F
class LR(torch.nn.Module):
    def __init__(self, n_input, n_output):
        super(LR, self).__init__()
        self.l1 = torch.nn.Linear(n_input, n_output)

    def forward(self, x):
        h1 = self.l1(x)
        h2 = torch.sigmoid(h1)
        return h2

model = LR(4, 3)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

from torch.autograd import Variable
loss_history = []
for epoch in range(1000):
    total_loss = 0
    for x_train, y_train in train_loader:
        x_train = Variable(x_train)
        y_train = Variable(y_train)
        optimizer.zero_grad()
        y_pred = model(x_train)
        loss = criterion(y_pred, y_train)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    loss_history.append(total_loss)
    if (epoch +1) % 100 == 0:
        print(epoch + 1, total_loss)

100 1.63955856859684
200 1.2039469927549362
300 0.9843573123216629
400 0.9481473788619041
500 0.847799651324749
600 0.857478104531765
700 0.8010830879211426
800 0.8148728087544441
900 0.8013908714056015
1000 0.7699911445379257

%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)

[<matplotlib.lines.Line2D at 0x7fc3317298d0>]

出力値が最大値になる品種が「予測された品種」であるとしたときの、正答率を求めましょう。

Y_pred = model.forward(X_train)
nrow, ncol = Y_pred.data.shape

count = 0
for i in range(nrow):
    cls = np.argmax(Y_pred.data[i, :])
    if cls == Y_ans_train[i]:
        count += 1

print(count, " / ", nrow, " = ", count / nrow)

65  /  75  =  0.8666666666666667

多層パーセプトロン Multi-Layer Perceptron (MLP)

これまで、Pytorch を用いた線形重回帰とロジスティック回帰モデルを作成してみました。同じような要領で、層を厚くしていくと「深層学習」になります。深層学習の中で最も単純なモデルが多層パーセプトロンです。

MLP による回帰

import numpy as np
from sklearn import datasets
iris = datasets.load_iris() # アヤメのデータの読み込み
data = iris.data.astype(np.float32)
X = data[:, :3] # アヤメの計測データのうち、最初の３つを説明変数とします。
Y = data[:, 3].reshape(len(data), 1) # 最後の１つを目的変数とします。

# 奇数番目のデータを教師データ、偶数番目のデータをテストデータとします。
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :] # 説明変数（教師データ）
X_test = X[index[index % 2 == 0], :] # 説明変数（テストデータ）
Y_train = Y[index[index % 2 != 0], :] # 目的変数（教師データ）
Y_test = Y[index[index % 2 == 0], :] # 目的変数（テストデータ）

import torch
X_train = torch.from_numpy(X_train).float()
X_test = torch.from_numpy(X_test).float()
Y_train = torch.from_numpy(Y_train).float()
Y_test = torch.from_numpy(Y_test).float()

from torch.utils.data import TensorDataset
train = TensorDataset(X_train, Y_train)

from torch.utils.data import DataLoader
train_loader = DataLoader(train, batch_size=10, shuffle=True)

#import torch.nn.functional as F
class MLPR(torch.nn.Module):
    def __init__(self, n_input, n_hidden, n_output):
        super(MLPR, self).__init__()
        self.l1 = torch.nn.Linear(n_input, n_hidden)
        self.l2 = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        h1 = self.l1(x)
        h2 = torch.sigmoid(h1)
        h3 = self.l2(h2)
        return h3

model = MLPR(3, 3, 1)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

from torch.autograd import Variable
loss_history = []
for epoch in range(1000):
    total_loss = 0
    for x_train, y_train in train_loader:
        x_train = Variable(x_train)
        y_train = Variable(y_train)
        optimizer.zero_grad()
        y_pred = model(x_train)
        loss = criterion(y_pred, y_train)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    loss_history.append(total_loss)
    if (epoch +1) % 100 == 0:
        print(epoch + 1, total_loss)

100 0.40582243632525206
200 0.3966686334460974
300 0.4202105160802603
400 0.3585368797648698
500 0.3776881340891123
600 0.3534861374646425
700 0.40271759033203125
800 0.37439848855137825
900 0.40052078012377024
1000 0.35703002475202084

%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)

[<matplotlib.lines.Line2D at 0x7fc3316929e8>]

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
plt.scatter(Y_train.flatten(), model.forward(X_train).data.flatten(), alpha=0.5)
plt.plot([min(Y), max(Y)], [min(Y), max(Y)])
plt.grid()
plt.legend()
plt.xlabel('Observed')
plt.ylabel('Predicted')
plt.show()

No handles with labels found to put in legend.

MLP による分類

import numpy as np
from sklearn import datasets
iris = datasets.load_iris() # アヤメのデータの読み込み
X = iris.data.astype(np.float32) # ４変数を説明変数に
Y = iris.target # アヤメの品種（３種）を目的変数に

# アヤメの品種を one-hot vector に変換します。
Y_ohv = np.zeros(3 * Y.size).reshape(Y.size, 3).astype(np.float32)
for i in range(Y.size):
    Y_ohv[i, Y[i]] = 1.0 # one-hot vector

# 奇数番目のデータを教師データ、偶数番目のデータをテストデータとします。
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :] # 説明変数（教師データ）
X_test = X[index[index % 2 == 0], :] # 説明変数（テストデータ）
Y_train = Y_ohv[index[index % 2 != 0], :] # 目的変数の one-hot vector （教師データ）
Y_test = Y_ohv[index[index % 2 == 0], :] # 目的変数の one-hot vector （テストデータ）
Y_ans_train = Y[index[index % 2 != 0]] # 目的変数（教師データ）
Y_ans_test = Y[index[index % 2 == 0]] # 目的変数（テストデータ）

import torch
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader

X_train = torch.from_numpy(X_train).float()
X_test = torch.from_numpy(X_test).float()
Y_train = torch.from_numpy(Y_train).float()
Y_test = torch.from_numpy(Y_test).float()

train = TensorDataset(X_train, Y_train)

train_loader = DataLoader(train, batch_size=10, shuffle=True)

class MLPC(torch.nn.Module):
    def __init__(self, n_input, n_hidden, n_output):
        super(MLPC, self).__init__()
        self.l1 = torch.nn.Linear(n_input, n_hidden)
        self.l2 = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        h1 = self.l1(x)
        h2 = torch.sigmoid(h1)
        h3 = self.l2(h2)
        h4 = torch.sigmoid(h3)
        return h4

model = MLPC(4, 3, 3)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

from torch.autograd import Variable
loss_history = []
for epoch in range(5000):
    total_loss = 0
    for x_train, y_train in train_loader:
        x_train = Variable(x_train)
        y_train = Variable(y_train)
        optimizer.zero_grad()
        y_pred = model(x_train)
        loss = criterion(y_pred, y_train)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    loss_history.append(total_loss)
    if (epoch +1) % 500 == 0:
        print(epoch + 1, total_loss)

500 1.645580604672432
1000 1.3838596642017365
1500 1.1801470965147018
2000 1.0481771975755692
2500 1.004256546497345
3000 0.9521581381559372
3500 0.9244466200470924
4000 0.8533390164375305
4500 0.845703762024641
5000 0.7936465740203857

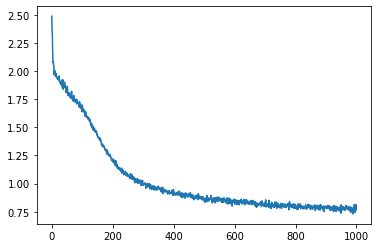
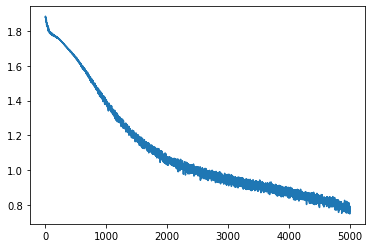
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)

[<matplotlib.lines.Line2D at 0x7fc331581c18>]

Y_pred = model.forward(X_train)
nrow, ncol = Y_pred.data.shape

count = 0
for i in range(nrow):
    cls = np.argmax(Y_pred.data[i, :])
    if cls == Y_ans_train[i]:
        count += 1

print(count, " / ", nrow, " = ", count / nrow)

67  /  75  =  0.8933333333333333

オートエンコーダー AutoEncoder (AE)

オートエンコーダーは、自分自身に回帰するニューラルネットワークです。入力層から中間層への変換器はエンコーダー encoder、中間層から出力層への変換器はデコーダー decoder と呼ばれます。中間層のニューロン数を入力データより少なくすることで「次元縮約」（次元削減）できます。

import numpy as np
from sklearn import datasets
iris = datasets.load_iris() # アヤメのデータの読み込み
data = iris.data.astype(np.float32)
X = data 

index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :] # 説明変数（教師データ）
X_test = X[index[index % 2 == 0], :] # 説明変数（テストデータ）

import torch
X_train = torch.from_numpy(X_train).float()
X_test = torch.from_numpy(X_test).float()

from torch.utils.data import TensorDataset
train = TensorDataset(X_train, X_train)

from torch.utils.data import DataLoader
train_loader = DataLoader(train, batch_size=10, shuffle=True)

class MLPR(torch.nn.Module):
    def __init__(self, n_input, n_hidden, n_output):
        super(MLPR, self).__init__()
        self.l1 = torch.nn.Linear(n_input, n_hidden)
        self.l2 = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        h1 = self.l1(x)
        h2 = torch.sigmoid(h1)
        h3 = self.l2(h2)
        return h3

    def project(self, x):
        h1 = self.l1(x)
        h2 = torch.sigmoid(h1)
        return h2

model = MLPR(4, 2, 4)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

from torch.autograd import Variable
loss_history = []
for epoch in range(500):
    total_loss = 0
    for x_train, y_train in train_loader:
        x_train = Variable(x_train)
        y_train = Variable(y_train)
        optimizer.zero_grad()
        y_pred = model(x_train)
        loss = criterion(y_pred, y_train)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    loss_history.append(total_loss)
    if (epoch +1) % 50 == 0:
        print(epoch + 1, total_loss)

50 7.260494828224182
100 3.8141910433769226
150 2.6670321971178055
200 1.9922174364328384
250 1.538402482867241
300 1.2299609556794167
350 1.1305854469537735
400 1.0665423274040222
450 1.0088475532829762
500 0.9823619686067104

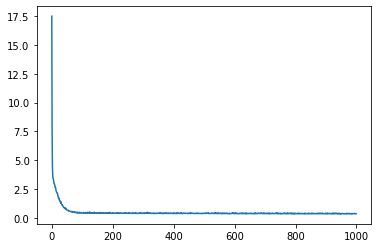
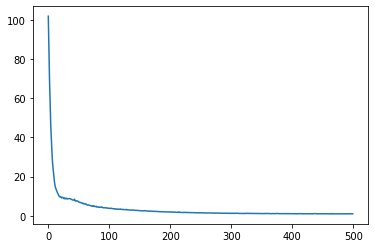
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)

[<matplotlib.lines.Line2D at 0x7fc33154e2e8>]

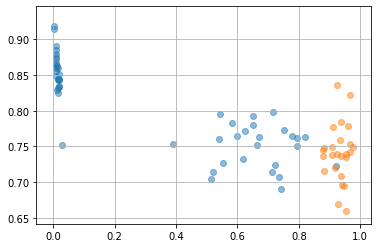
中間層に投影されたデータを見る

latent = model.project(X_train)

%matplotlib inline
import matplotlib.pyplot as plt
plt.scatter(latent.data[0:50, 0], latent.data[0:50, 1], alpha=0.5)
plt.scatter(latent.data[50:100, 0], latent.data[50:100, 1], alpha=0.5)
plt.scatter(latent.data[100:150, 0], latent.data[100:150, 1], alpha=0.5)
plt.grid()

課題

• 上記のモデルについて、テストセットの予測性能を評価しなさい。

• 線形重回帰、ロジスティック回帰、多層パーセプトロン、オートエンコーダーを比較し、その違いと共通点について説明しなさい。