補間やカーブフィッティングなどの最適化

実験などにより得られた観測値は、普通は飛び飛びの値になりますが、その間の値を求めたい時があります。その時に用いるのが、種々の補間法（補完ではありません）と、その他のカーブフィッティング（曲線近似）です。これらの解法は、プログラミング演習の題材としてよく使われますが、実用上は強力なライブラリが多数存在しますので、自作するよりも既存のライブラリを使ったほうが便利です。

計算機実験

ここでは、計算機実験として、以下の3つの数学関数 f(x), g(x), h(x) を用意します。

import numpy as np
f = lambda x: 1/(1 + np.exp(-x))
g = lambda x: 1.0/(1.0+x**2)
h = lambda x: np.sin(x)

上記3つの数学関数が実際に起きている現象を示すものとします。

実験による観測値

ですが実際には、実験で得られる観測点は、次のように飛び飛びの値です。

x_observed = np.linspace(-10, 10, 11)
x_observed

array([-10.,  -8.,  -6.,  -4.,  -2.,   0.,   2.,   4.,   6.,   8.,  10.])

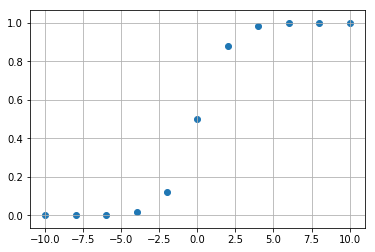
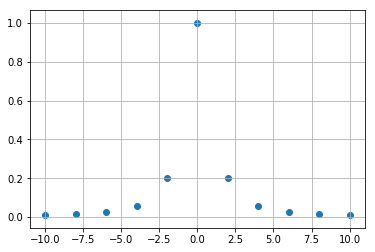
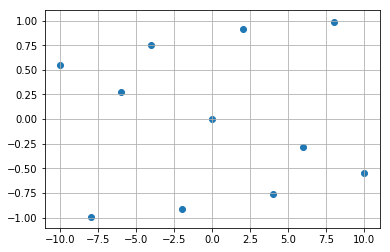
このとき、実験によってどのような値が観測されるか図示してみましょう。

%matplotlib inline
import matplotlib.pyplot as plt

for func in [f, g, h]:
    y_observed = func(x_observed)
    plt.scatter(x_observed, y_observed)
    plt.grid()
    plt.show()

以上のような観測値から、どのようなカーブ（曲線）が想像できるでしょうか。

観測されない真実の姿

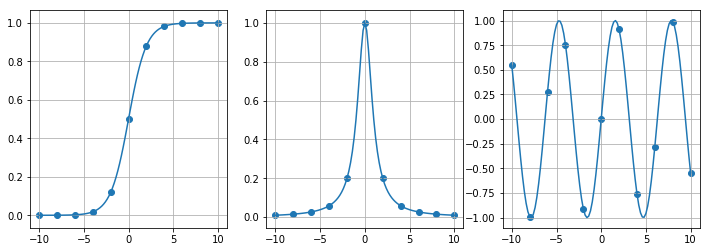
実験では観測されない真実の姿を図示してみましょう。

x_latent = np.linspace(-10, 10, 101)
x_latent

array([-10. ,  -9.8,  -9.6,  -9.4,  -9.2,  -9. ,  -8.8,  -8.6,  -8.4,
        -8.2,  -8. ,  -7.8,  -7.6,  -7.4,  -7.2,  -7. ,  -6.8,  -6.6,
        -6.4,  -6.2,  -6. ,  -5.8,  -5.6,  -5.4,  -5.2,  -5. ,  -4.8,
        -4.6,  -4.4,  -4.2,  -4. ,  -3.8,  -3.6,  -3.4,  -3.2,  -3. ,
        -2.8,  -2.6,  -2.4,  -2.2,  -2. ,  -1.8,  -1.6,  -1.4,  -1.2,
        -1. ,  -0.8,  -0.6,  -0.4,  -0.2,   0. ,   0.2,   0.4,   0.6,
         0.8,   1. ,   1.2,   1.4,   1.6,   1.8,   2. ,   2.2,   2.4,
         2.6,   2.8,   3. ,   3.2,   3.4,   3.6,   3.8,   4. ,   4.2,
         4.4,   4.6,   4.8,   5. ,   5.2,   5.4,   5.6,   5.8,   6. ,
         6.2,   6.4,   6.6,   6.8,   7. ,   7.2,   7.4,   7.6,   7.8,
         8. ,   8.2,   8.4,   8.6,   8.8,   9. ,   9.2,   9.4,   9.6,
         9.8,  10. ])

fig_idx = 0
plt.figure(figsize=(12,4))
for func in [f, g, h]:
    fig_idx += 1
    y_observed = func(x_observed)
    y_latent = func(x_latent)
    plt.subplot(1, 3, fig_idx)
    plt.scatter(x_observed, y_observed)
    plt.plot(x_latent, y_latent)
    plt.grid()
plt.show()

さて、ここで求めたいことは、限られた観測値から、この「真実の姿」にどれだけ近いものを導き出せるかということです。

Scipy.interpolate による補間

scipy には interpolate という強力なライブラリが用意されていて、様々な補間法が使えます。

from scipy import interpolate

ip1 = ["最近傍点補間", lambda x, y: interpolate.interp1d(x, y, kind="nearest")]
ip2 = ["線形補間", interpolate.interp1d]
ip3 = ["ラグランジュ補間", interpolate.lagrange]
ip4 = ["重心補間", interpolate.BarycentricInterpolator]
ip5 = ["Krogh補間", interpolate.KroghInterpolator]
ip6 = ["2次スプライン補間", lambda x, y: interpolate.interp1d(x, y, kind="quadratic")]
ip7 = ["3次スプライン補間", lambda x, y: interpolate.interp1d(x, y, kind="cubic")]
ip8 = ["秋間補間", interpolate.Akima1DInterpolator]
ip9 = ["区分的 3 次エルミート補間", interpolate.PchipInterpolator]

x_observed = np.linspace(-10, 10, 11)
x_observed

array([-10.,  -8.,  -6.,  -4.,  -2.,   0.,   2.,   4.,   6.,   8.,  10.])

y_observed = f(x_observed)
y_latent = f(x_latent)
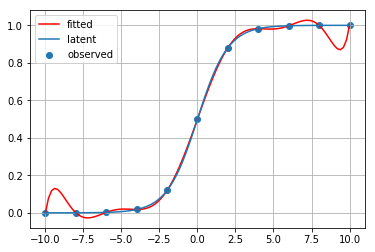
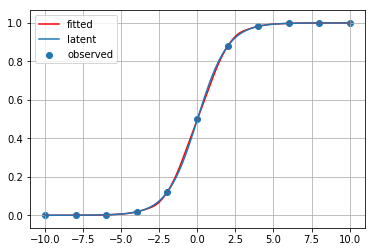
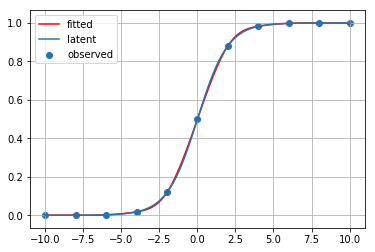
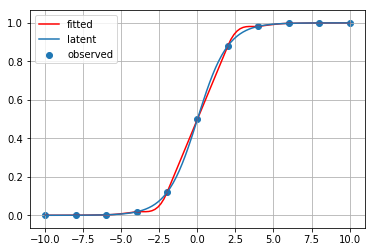
for method_name, method in [ip1, ip2, ip3, ip4, ip5, ip6, ip7, ip8, ip9]:
    print(method_name)
    fitted_curve = method(x_observed, y_observed)
    plt.scatter(x_observed, y_observed, label="observed")
    plt.plot(x_latent, fitted_curve(x_latent), c="red", label="fitted")
    plt.plot(x_latent, y_latent, label="latent")
    plt.grid()
    plt.legend()
    plt.show()

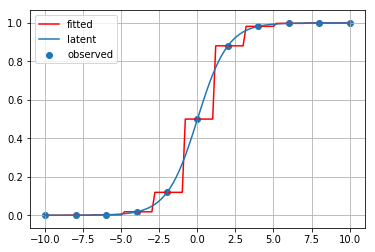
最近傍点補間

線形補間

ラグランジュ補間

重心補間

Krogh補間

2次スプライン補間

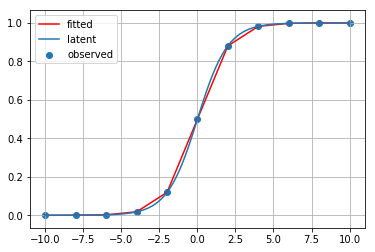
3次スプライン補間

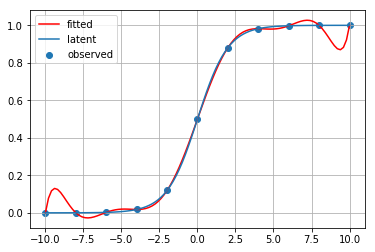
秋間補間

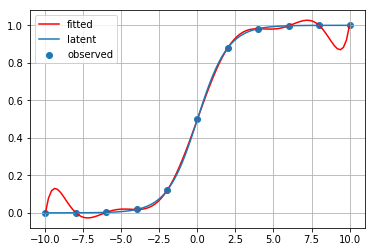
区分的 3 次エルミート補間

課題1

• g(x) を様々な補間法で補間してください。

• h(x) を様々な補間法で補間してください。

• 次の測定値を様々な補間法で補間してください。

x_observed = np.array([9, 28, 38, 58, 88, 98, 108, 118, 128, 138, 148, 158, 168, 178, 188, 198, 208, 218, 228, 238, 278, 288, 298])
y_observed = np.array([51, 80, 112, 294, 286, 110, 59, 70, 56, 70, 104, 59, 59, 72, 87, 99, 64, 60, 74, 151, 157, 57, 83])

x_latent = np.linspace(min(x_observed), max(x_observed), 100)

Numpy.polyfit によるカーブフィッティング

Numpy の .polfyfit を用いると、最小2乗法によるカーブフィッティングが簡単にできます。改めて、実験により観測された飛び飛びの観測値を計算し直しておくと

x_observed = np.linspace(-10, 10, 11)
x_observed

array([-10.,  -8.,  -6.,  -4.,  -2.,   0.,   2.,   4.,   6.,   8.,  10.])

y_observed = f(x_observed)
y_observed

array([4.53978687e-05, 3.35350130e-04, 2.47262316e-03, 1.79862100e-02,
       1.19202922e-01, 5.00000000e-01, 8.80797078e-01, 9.82013790e-01,
       9.97527377e-01, 9.99664650e-01, 9.99954602e-01])

上記の x, y に対して、最小2乗法による線形回帰を行うと

coefficients = np.polyfit(x_observed, y_observed, 1)
coefficients

array([0.06668944, 0.5       ])

上記の戻り値がそのまま y = ax + b の係数 a, b に相当します。Sympyを用いて表すと、

import sympy as sym
from sympy.plotting import plot
sym.init_printing(use_unicode=True)
%matplotlib inline

x, y = sym.symbols("x y")

# Google Colab 使用の場合、SympyによるTeX表示をサポートするために実行する
def custom_latex_printer(exp,**options):
    from google.colab.output._publish import javascript
    url = "https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.3/latest.js?config=default"
    javascript(url=url)
    return sym.printing.latex(exp,**options)

sym.init_printing(use_latex="mathjax",latex_printer=custom_latex_printer)

expr = 0
for index, coefficient in enumerate(coefficients):
    expr += coefficient * x ** (len(coefficients) - index - 1)
display(sym.Eq(y, expr))

$$y = 0.0666894399883493 x + 0.5$$

というのが、得られた回帰式です。

最後の引数で何次式に回帰するかが指定できます。たとえば３次式にフィッティングしたければ

coefficients = np.polyfit(x_observed, y_observed, 3)

expr = 0
for index, coefficient in enumerate(coefficients):
    expr += coefficient * x ** (len(coefficients) - index - 1)
display(sym.Eq(y, expr))

$$y = - 0.000746038674650085 x^{3} + 0.119807393623435 x + 0.5$$

に回帰できたことを示しています。

得られたカーブを描くためには、複数のxとそれに対応するyが必要ですが、それは以下のように得られます。

fitted_curve = np.poly1d(np.polyfit(x_observed, y_observed, 3))(x_latent)
fitted_curve

array([ 0.04796474,  0.02805317,  0.00989629, -0.00654171, -0.02129666,
       -0.03440435, -0.0459006 , -0.05582121, -0.064202  , -0.07107878,
       -0.07648735, -0.08046353, -0.08304312, -0.08426194, -0.08415579,
       -0.08276049, -0.08011184, -0.07624566, -0.07119776, -0.06500394,
       -0.05770001, -0.04932179, -0.03990508, -0.02948569, -0.01809944,
       -0.00578213,  0.00743042,  0.02150241,  0.03639803,  0.05208146,
        0.0685169 ,  0.08566854,  0.10350056,  0.12197717,  0.14106254,
        0.16072086,  0.18091634,  0.20161315,  0.22277549,  0.24436755,
        0.26635352,  0.28869759,  0.31136394,  0.33431678,  0.35752028,
        0.38093865,  0.40453606,  0.42827671,  0.45212479,  0.47604449,
        0.5       ,  0.52395551,  0.54787521,  0.57172329,  0.59546394,
        0.61906135,  0.64247972,  0.66568322,  0.68863606,  0.71130241,
        0.73364648,  0.75563245,  0.77722451,  0.79838685,  0.81908366,
        0.83927914,  0.85893746,  0.87802283,  0.89649944,  0.91433146,
        0.9314831 ,  0.94791854,  0.96360197,  0.97849759,  0.99256958,
        1.00578213,  1.01809944,  1.02948569,  1.03990508,  1.04932179,
        1.05770001,  1.06500394,  1.07119776,  1.07624566,  1.08011184,
        1.08276049,  1.08415579,  1.08426194,  1.08304312,  1.08046353,
        1.07648735,  1.07107878,  1.064202  ,  1.05582121,  1.0459006 ,
        1.03440435,  1.02129666,  1.00654171,  0.99010371,  0.97194683,
        0.95203526])

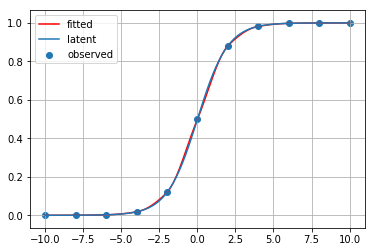
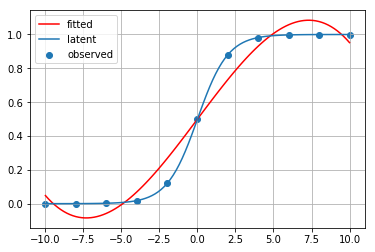
plt.scatter(x_observed, f(x_observed), label="observed")
plt.plot(x_latent, fitted_curve, c="red", label="fitted")
plt.plot(x_latent, f(x_latent), label="latent")
plt.grid()
plt.legend()

<matplotlib.legend.Legend at 0x7fb673a3c630>

課題2

• g(x) を５次式で近似してください。

• h(x) を９次式で近似してください。

• 次の測定値を９次式で近似してください。

x_observed = np.array([9, 28, 38, 58, 88, 98, 108, 118, 128, 138, 148, 158, 168, 178, 188, 198, 208, 218, 228, 238, 278, 288, 298])
y_observed = np.array([51, 80, 112, 294, 286, 110, 59, 70, 56, 70, 104, 59, 59, 72, 87, 99, 64, 60, 74, 151, 157, 57, 83])

Scipy.optimize.curve_fit によるカーブフィッティング

Pythonを使ってカーブフィッティング（曲線近似）する方法として、 scipy.optimize.curve_fit を使う方法があります。

用いる実験値

x_observed = [9, 28, 38, 58, 88, 98, 108, 118, 128, 138, 148, 158, 168, 178, 188, 198, 208, 218, 228, 238, 278, 288, 298]
y_observed = [51, 80, 112, 294, 286, 110, 59, 70, 56, 70, 104, 59, 59, 72, 87, 99, 64, 60, 74, 151, 157, 57, 83]

Python の List 型から、Numpy の Array 型に変換しておきましょう。

import numpy as np
x_observed = np.array(x_observed)
y_observed = np.array(y_observed)

１次式近似

まず、１次式に近似してみましょう。関数 func1 を定義します。a と b が、求めたい値になります。

def func1(X, a, b): # １次式近似
    Y = a + b * X
    return Y

関数 func1 の使用例はこちらです。

func1(x_observed, 2, 2)

array([ 20,  58,  78, 118, 178, 198, 218, 238, 258, 278, 298, 318, 338,
       358, 378, 398, 418, 438, 458, 478, 558, 578, 598])

さて、scipy.optimize.curve_fit を使って近似してみましょう。

from scipy.optimize import curve_fit  
popt, pcov = curve_fit(func1,x_observed,y_observed) # poptは最適推定値、pcovは共分散
popt

array([125.77023172,  -0.1605313 ])

ここで得られた popt が最適推定値を格納しています。Numpy.polyfit を使ったカーブフィッティング で得られた推定値と比較してみましょう。

２次式近似

次に、２次式に近似してみましょう。関数 func2 を定義します。a と b と c が、求めたい値になります。

def func2(X, a, b, c): # 2次式近似
    Y = a + b * X + c * X ** 2
    return Y

関数 func2 の使用例はこちらです。

func2(x_observed, 2, 2, 2)

array([   182,   1626,   2966,   6846,  15666,  19406,  23546,  28086,
        33026,  38366,  44106,  50246,  56786,  63726,  71066,  78806,
        86946,  95486, 104426, 113766, 155126, 166466, 178206])

さて、scipy.optimize.curve_fit を使って近似してみましょう。

from scipy.optimize import curve_fit  
popt, pcov = curve_fit(func2,x_observed,y_observed) # poptは最適推定値、pcovは共分散
popt

array([ 1.39787684e+02, -4.07809516e-01,  7.97183226e-04])

ここで得られた popt が最適推定値を格納しています。Numpy.polyfit を使ったカーブフィッティング で得られた推定値と比較してみましょう。

次のようにすれば、最適推定値を用いた近似曲線が描けます。

func2(x_observed, 1.39787684e+02, -4.07809516e-01,  7.97183226e-04)

array([136.1819702 , 128.9940092 , 125.44205497, 118.81645644,
       110.07383349, 107.47849913, 105.04260142, 102.76614035,
       100.64911593,  98.69152815,  96.89337701,  95.25466253,
        93.77538468,  92.45554348,  91.29513893,  90.29417102,
        89.45263976,  88.77054514,  88.24788717,  87.88466585,
        88.02614699,  88.46010889,  89.05350743])

３次式近似

同様に、３次式に近似してみましょう。関数 func3 を定義します。a と b と c と d が、求めたい値になります。

def func3(X, a, b, c, d): # 3次式近似
    Y = a + b * X + c * X ** 2 + d * X ** 3
    return Y

さて、scipy.optimize.curve_fit を使って近似してみましょう。

from scipy.optimize import curve_fit  
popt, pcov = curve_fit(func3,x_observed,y_observed) # poptは最適推定値、pcovは共分散
popt

array([ 7.84214107e+01,  1.88213104e+00, -1.74165777e-02,  3.89638087e-05])

ここで得られた popt が最適推定値を格納しています。Numpy.polyfit を使ったカーブフィッティング で得られた推定値と比較してみましょう。

次のようにすれば、最適推定値を用いた近似曲線が描けます。

func3(x_observed, 7.84214107e+01,  1.88213104e+00, -1.74165777e-02,  3.89638087e-05)

array([ 93.97825188, 118.32181643, 126.93087413, 136.59795028,
       135.72770915, 132.27386543, 127.62777811, 122.02323006,
       115.69400413, 108.87388316, 101.79665001,  94.69608754,
        87.80597859,  81.36010602,  75.59225267,  70.73620141,
        67.02573508,  64.69463654,  63.97668864,  65.10567422,
        92.76660851, 106.63700433, 123.75703075])

何次式になっても使える汎用的な関数を作りたい

今まで１次式、２次式、３次式と別々の関数を作りましたが、これだと面倒すぎるので、何次式になっても使える汎用的な関数を作りましょう。何次式に近似するかはパラメータの数で自動的に判定するようにします。

import numpy as np
def func(X, *params):
    Y = np.zeros_like(X)
    for i, param in enumerate(params):
        Y = Y + np.array(param * X ** i)
    return Y

次の２つのコードを実行して、上記の func2 による計算結果と、func3 による計算結果と同じであることを確認しましょう。

func(x_observed, 1.39787684e+02, -4.07809516e-01,  7.97183226e-04)

array([136.1819702 , 128.9940092 , 125.44205497, 118.81645644,
       110.07383349, 107.47849913, 105.04260142, 102.76614035,
       100.64911593,  98.69152815,  96.89337701,  95.25466253,
        93.77538468,  92.45554348,  91.29513893,  90.29417102,
        89.45263976,  88.77054514,  88.24788717,  87.88466585,
        88.02614699,  88.46010889,  89.05350743])

func(x_observed, 7.84214107e+01,  1.88213104e+00, -1.74165777e-02,  3.89638087e-05)

array([ 93.97825188, 118.32181643, 126.93087413, 136.59795028,
       135.72770915, 132.27386543, 127.62777811, 122.02323006,
       115.69400413, 108.87388316, 101.79665001,  94.69608754,
        87.80597859,  81.36010602,  75.59225267,  70.73620141,
        67.02573508,  64.69463654,  63.97668864,  65.10567422,
        92.76660851, 106.63700433, 123.75703075])

何次式になっても使える汎用的な関数による多項式近似

ここまでくれば、何次式にでも多項式近似できます。ただし、パラメータの数を指定するために p0= で初期値を必要数だけ入力する必要が生じます。

from scipy.optimize import curve_fit  
popt, pcov = curve_fit(func,x_observed,y_observed, p0=[1, 1]) 
popt

array([125.77023172,  -0.1605313 ])

from scipy.optimize import curve_fit  
popt, pcov = curve_fit(func,x_observed,y_observed, p0=[1, 1, 1]) 
popt

array([ 1.39787684e+02, -4.07809516e-01,  7.97183226e-04])

from scipy.optimize import curve_fit  
popt, pcov = curve_fit(func,x_observed,y_observed, p0=[1, 1, 1, 1]) 
popt

array([ 7.84214107e+01,  1.88213104e+00, -1.74165777e-02,  3.89638087e-05])

from scipy.optimize import curve_fit  
popt, pcov = curve_fit(func,x_observed,y_observed, p0=[1, 1, 1, 1, 1]) 
popt

array([-7.54495613e+01,  1.13179580e+01, -1.50591743e-01,  7.02970546e-04,
       -1.07313869e-06])

Numpy.polyfit を使ったカーブフィッティングとの比較

上記の計算結果を、Numpy.polyfit を使ったカーブフィッティング で得られた推定値と比較してみましょう。

Numpy.polyfit は、多項式近似するだけなら、便利で使いやすいですが、多項式近似しかできません。もっと他の関数で近似したい場合は、scipy.optimize.curve_fit の使い方を理解するのが良いでしょう。

他にどんな最適化手法があるか知りたい

「optimize?」とすると、他の方法についてもいろいろ説明してあります。英語ですけど。

from scipy import optimize
optimize?

ググってももちろん良いんですが、「?」を使うとダイレクトにその説明に行けて、しかもオフラインでも使えるのが良いですね。

ニュートン法と二分法

方程式 f(x) = 0 の解を求める方法として代表的なものに、二分法とニュートン法があります。例として、こんな関数を使います。

import math
def f(x):
    return math.exp(x) - 3 * x

import math
f = lambda x: math.exp(x) - 3 * x

scipy という科学技術計算用のライブラリが便利です。

from scipy import optimize

二分法

二分法は、関数 y=f(x)が区間[a,b]で連続で、解が1つ存在するときに使えます。たとえば区間[0,1]の中に解があるとわかってる場合は

optimize.bisect(f, 0, 1)

0.619061286737633

あら簡単。

ニュートン法

ニュートン法は、関数y=f(x)が単調連続で変曲点がなく、かつf(x)の導関数が求められるときに使えます。f(x)=0のときのxを求めたいときは

optimize.newton(f, 0)

0.6190612867359452

あら簡単。

もっと詳しい使い方を知りたい

「?」を使うと、パラメーターの説明や使用例などが確認できます。英語ですけど。

optimize.bisect?

optimize.newton?