「Morgan Fingerprint」 ってよォ〜〜...あるよなァ...
RDKit とかで計算できる、化合物を「部分構造のベクトル」で表現するヤツよぉ...
そうすっとよォ... Ligand-based screening とかで「創薬」に使えるわけだ...
ところがだッ!!!
あれってなァ... 「次元」が高すぎんだよォ!! そのくせ「スパース」すぎんだよッ!!
ふざけやがって! AutoEncoder で、テメェの次元をどのくらい削減できるか試してやろうぜエェェェーッ!!
解析の流れ
ドドドドド...
PCCDB データ
PCCDB ってあるだろ...知らねえだとッ!?
Public Computational Chemistry Database だよッ!
そいつを使って「ベンチマーク」ってヤツをよォ...トコトンやってやるぜ...
PCCDB の全データを使うのもナンだからよォ...「先頭2000個のみ」にするッ!
「データを見せろ」だとォ!
自分で取得しやがれッ!
しょぉ〜〜がねえからサイズだけ教えてやるッ!
2000 rows × 21 columns
ここから先のコードはよォ...全部 「Google Colab」 上で実行してやったぜ...
RDKit のインストール
Google Colab 上で 「RDKit」 が使えねえだとォッ!?
を参考に自力でインストールしやがれッ!
MFを算出
テメェの名前は何だ? 「Morgan Fingerprint」??...贅沢な名前だなァ...
いいかッ! テメェの名は今から MF と略すッ! 分かったか MF ッ!!
PCCDBデータにある化合物のSMILES表記から、次のようにして MF を算出し、高次元ベクトルに変換してやるぜ...言っただろうがよォ〜〜〜...トコトンやるってなッ!!
import numpy as np
from rdkit import Chem
from rdkit.Chem import AllChem
morgans = [] # 算出した MF を格納
no_error = [] # エラーなく計算できたIDを格納
for idx, smile in enumerate(df1['smiles']): # df1 に PCCDB データが pandas DataFrame 型で入ってる
mol = Chem.MolFromSmiles(smile)
try:
fp = AllChem.GetMorganFingerprint(mol, 2) # MF を算出
except:
continue
no_error.append(idx)
morgans.append(fp.GetNonzeroElements())
morgan_keys = [] # 全化合物のMFキーを格納
for morgan in morgans:
morgan_keys += morgan.keys()
morgan_keys = list(set(morgan_keys))
morgan_mat = np.zeros((len(morgans), len(morgan_keys))) # 全化合物のMF行列
for idx1, morgan in enumerate(morgans):
for k, v in morgan.items():
morgan_mat[idx1][morgan_keys.index(k)] = v
MFってよォ...実はたくさん種類があるんだよな...
- radius をいくつにするか
- bit vector にするか count-based vector にするか
- hash するかしないか
今回はよォ...
- radius = 2, count-based, unhashed MF
- radius = 4, count-based, unhashed MF
について計算してやったぜ...
それぞれ MF2, MF4 と命名してやるッ!
計算したMF行列のサイズを今から見せてやるぜ...
MF2
1917 rows × 6487 columns
MF4
1917 rows × 14339 columns
おいッ!
「2000化合物」も入力してやったのに、使えるヤツぁ〜たった「1917化合物」かよッ!! 「83化合物」もエラーを起こしてやがるぜッ!! フヌケがぁ〜〜〜ッ!!
で、 unhashed にすると、列の数が 6487 と 14339 だとよッ! なあッ、次元がクソ高ェだろッ! こんな「高次元」が!「本当に必要」なのかよッ!!!
この中で、「ゼロ」が異様に目につきやがるので、「何%がゼロなのか」今から数えてやるッ!
s_bool = pd.DataFrame(morgan_mat) == 0.0
s_bool.sum().sum() / (len(morgans) * len(morgan_keys))
MF2
0.9970657578549419
MF4
0.9982852431998807
「99%以上がゼロ」だとォ〜〜〜ッ!!! フザケやがって! この「スパースな行列」野郎〜〜〜ッ!!
このオレがッ! 予測性能を落とさず! 次元削減してやるぜエェェーッ!! 覚悟してろッ!!!
ドドドドド...
MF を直接使ってMLP回帰
今回、「予測対象となる物性」を発表するッ! 以下の9種類の物性だッ!! 意味はテメェで調べやがれッ!
target_names = ['TPSA', 'dipole', 'excitation_energy_1',
'homo_energy', 'homo_lumo_gap', 'logP', 'lumo_energy', 'melting_point',
'molecular_refractivity']
この「予測対象となる物性」がよォ〜〜...機械学習における「目的変数」になるわけだな...
「機械学習」つっても、色々あんだろ? 今から何するか分かるか?
「教師あり機械学習」の「回帰」だろうがよォ〜〜〜ッ!!!
「回帰手法」も色々あるんだぜ...それこそ「スタンド使い」の数くらいある...
その中で、オレが選んだ手法は分かるか?
AutoEncoderと関連があって、次元削減しながら予測する教師あり機械学習手法...
ゴゴゴゴゴゴ...
喰らえッ! 必殺! Multi-Layer Perceptron (MLP)ッ!!!
ズギュウゥゥゥーン!!!
import timeit
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
hidden_layer_sizes = [250, 1000, 2000] # 隠れ層のサイズ
curve_test0 = {}
curve_train0 = {}
curve_seconds0 = {}
X = morgan_mat
y = df1.iloc[no_error]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4)
for target_name in target_names:
for hidden_layer_size in hidden_layer_sizes:
regressor = MLPRegressor(hidden_layer_sizes=(hidden_layer_size,),
max_iter=10000) # 回帰器の生成
seconds = timeit.timeit(lambda: regressor.fit(X_train, y_train[target_name]),
number=1)
score_train = regressor.score(X_train, y_train[target_name])
score_test = regressor.score(X_test, y_test[target_name])
print(target_name, hidden_layer_size, seconds)
print("\t", score_train, score_test)
if target_name not in curve_test0.keys():
curve_test0[target_name] = []
curve_test0[target_name].append(score_test)
if target_name not in curve_train0.keys():
curve_train0[target_name] = []
curve_train0[target_name].append(score_train)
if target_name not in curve_seconds0.keys():
curve_seconds0[target_name] = []
curve_seconds0[target_name].append(seconds)
テメェのちっぽけな脳みそでよォ、 MFの次元を覚えてやがるか?
MF2 は 6487 次元、 MF4 は 14339 次元だっただろ...
そいつをよォ...オレのMLPで、隠れ層のサイズを 2000次元 1000次元 250次元 と絞っていったときに、予測性能がどの程度下がるか計算してやったぜ...
%matplotlib inline
import matplotlib.pyplot as plt
for target_name in target_names:
plt.title(target_name)
plt.ylim([0, 1.1])
plt.plot(hidden_layer_sizes, curve_train0[target_name],
marker='o', label="MF2 train")
plt.plot(hidden_layer_sizes, curve_test0[target_name],
marker='o', label="MF2 test")
plt.grid()
plt.legend()
plt.show()
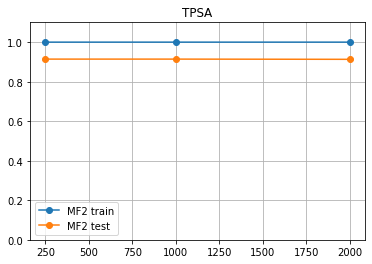
TPSAの予測結果だけ見せてやる...いいか、横軸は「隠れ層のサイズ」、縦軸は「R2値」だぜ...
なぁ、見てみろよ...「隠れ層の数を 250次元 まで減らしても、予測精度はほとんど変わんねぇ」ってことだ... MF2 は 「6487 次元」 もあったクセによオォォォ!! こいつァ〜とんだスパース行列だぜッ!!!
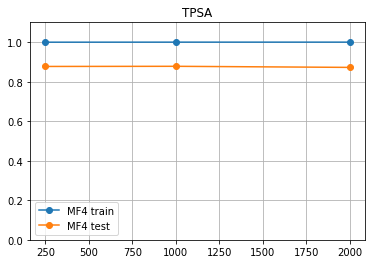
おい、せっかくだから MF4 の結果も見てみるか?
MF4 なんてよォ、 14339 次元もあったクセに、やっぱり 250次元 まで減らしても予測精度はほとんど変わんねぇんだぜ!!
しかも、だ!
MF4 は MF2 と比べて、「学習に使わなかったデータの予測性能が低い」ことが分かるッ!! これは予測対象の性質に依るのか? せっかく radius を広げて情報量を増やしたのにこのザマだ!!
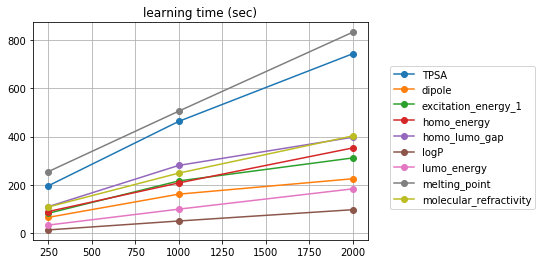
計算時間はどうなるか想像できるか? まあ見てみろよ...
%matplotlib inline
import matplotlib.pyplot as plt
for target_name in target_names:
plt.title("learning time (sec)")
plt.plot(hidden_layer_sizes, curve_seconds0[target_name],
marker='o', label=target_name)
plt.grid()
plt.legend(loc = 'upper right',
bbox_to_anchor = (1, 0.7, 0.5, 0.1),
borderaxespad = 0.0)
plt.show()
MF2
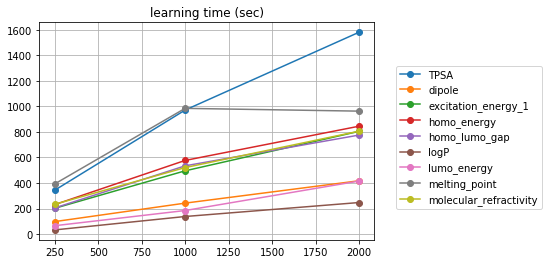
MF4
「隠れ層の数にほぼ比例」してやがるぜ...こいつらよォ...
よ〜〜〜〜く分かっただろ...MFは 「250次元」 に圧縮しても大丈夫ってことだ...
それ以上の次元は「無駄」ってわけだな...
なら、何次元までなら次元削減して大丈夫か?
興味があるヤツぁ、「最適なパラメータを効率的に探索しちゃおっちゅうな(Optuna)」でも参考にして、テメェでパラメータ・チューニングしやがれ!!!
オレは「別の解析」をヤるッ!!!
ドドドドド...
MF を AE して、その潜在空間上のベクトルで MLP 回帰
次によォ...オレは考えたんだ...
「クソ高次元のMFを使ってMLPで物性予測をしたとき、隠れ層の次元は低くても良い」
ならば、
「低次元の隠れ層を持つオートエンコーダーを使えば、クソ高次元のMFを低次元に写像することで、予測性能を落とさずに計算時間を短縮できるのではないか?」
となッ!!...どうだァ〜ッ!このオレの頭のキレはよォ〜ッ!
オートエンコーダーの「隠れ層の次元」は、細かく試してやったぜ...言っただろうがよぉ〜〜〜...トコトンやるってな!!!
hidden_layer_sizes = [250, 500, 750, 1000, 1250, 1500, 1750, 2000]
これがコードだ... まずMFを、「自分自身に回帰する」オートエンコーダーで回帰する...次に、「学習後のオートエンコーダー」を使って、MFを低次元に写像する...最後に、「低次元に写像したMF」を使って物性予測する...
import timeit
curve_test2 = {}
curve_train2 = {}
curve_seconds2 = {}
for h in hidden_layer_sizes:
ae = MLPRegressor(hidden_layer_sizes=(h,), max_iter=10000) # オートエンコーダー
seconds_ae = timeit.timeit(lambda: ae.fit(morgan_mat, morgan_mat), number=1)
print("AE ", h, " took ", seconds_ae, " sec.")
X = np.array(morgan_mat).dot(ae.coefs_[0]) # オートエンコーダーでMFを低次元へ写像
for target_name in target_names:
regressor = MLPRegressor(hidden_layer_sizes=(250,), max_iter=10000) # MLP回帰(隠れ層は250次元に固定)
seconds = timeit.timeit(lambda: regressor.fit(X_train, y_train[target_name]),
number=1)
score_train = regressor.score(X_train, y_train[target_name])
score_test = regressor.score(X_test, y_test[target_name])
print("MLP ", h, " (", target_name, ") took ", seconds, " sec.")
print(score_train, score_test)
if target_name not in curve_test2.keys():
curve_test2[target_name] = []
curve_test2[target_name].append(score_test)
if target_name not in curve_train2.keys():
curve_train2[target_name] = []
curve_train2[target_name].append(score_train)
if target_name not in curve_seconds2.keys():
curve_seconds2[target_name] = []
curve_seconds2[target_name].append(seconds)
これが、「予測性能を比較する」ためのコード...
%matplotlib inline
import matplotlib.pyplot
for target_name in target_names:
plt.title(target_name)
plt.plot(hidden_layer_sizes, curve_train2[target_name],
marker='x', label="MF2AE train")
plt.plot(hidden_layer_sizes, curve_test2[target_name],
marker='x', label="MF2AE test")
plt.plot([250, 1000, 2000], curve_train0[target_name],
marker='o', label="MF2 train")
plt.plot([250, 1000, 2000], curve_test0[target_name],
marker='o', label="MF2 test")
plt.grid()
plt.legend()
plt.show()
これが「学習時間を比較する」コードだ...
%matplotlib inline
import matplotlib.pyplot as plt
for target_name in target_names:
plt.title("learning time (sec)")
plt.plot(hidden_layer_sizes, curve_seconds2[target_name],
marker='o', label=target_name)
plt.grid()
plt.legend(loc = 'upper right',
bbox_to_anchor = (1, 0.7, 0.5, 0.1),
borderaxespad = 0.0)
plt.show()
解析結果
ゴゴゴゴゴゴ...
予測性能 (R2値)
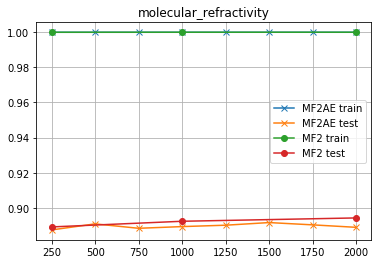
「MFを直接使ったMLP回帰」の結果も載せてやったぜ...
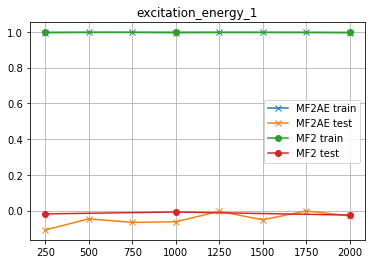
たとえば 「MF2 test」 は「MF2を直接使ったMLP回帰(テストデータ)」の結果で、横軸は「そのMLPの隠れ層の次元」だ...
そしてッ!「MF2AE test」は「MF2をオートエンコーダーで低次元に写像して、その写像したベクトルを使ったMLP回帰(テストデータ)」の結果で、横軸は「そのオートエンコーダーの隠れ層の次元」だ!MLPの隠れ層の次元は250次元で固定してあるッ!
縦軸は、予測精度 R2値だ...
「高い予測精度をキープする」
「計算時間は短くする」
「両方」やらなくちゃあいけないのが「計算科学者」の辛いところだな...覚悟はいいか...オレはできている...
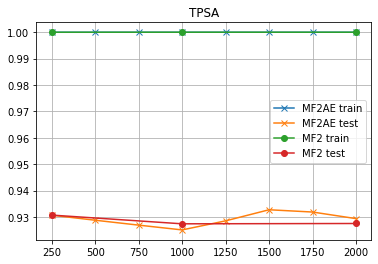
TPSA
- MF2
直接MLP使った時は、「隠れ層を下手に高次元にすると予測精度が落ちる」傾向があるようだな...「オーバーフィッティング」ってヤツだな...「時間ばっかりかかる」クセによ...ところがAEを使った場合は、「次元数は高めの方が良いかもしれない」ようだぜ...誤差の範囲内かも知れんがな...
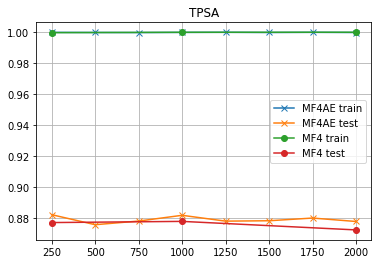
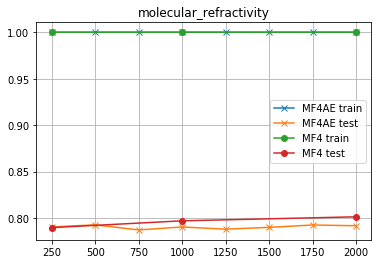
- MF4
前にも言ったが、「MF4を使うとかえって性能が落ちる」ようだ...それ以外は、MF2と傾向が同じようだな...
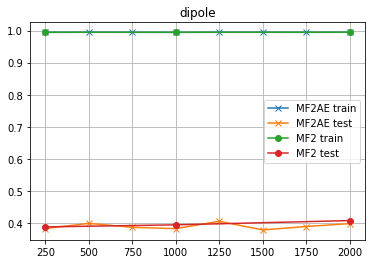
dipole
- MF2
おいッ! 予測性能が低すぎるぜッ! ちょっと「話にならんレベル」だな...
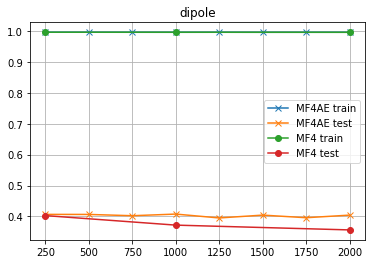
- MF4
予測性能が低くて使えんが、「AEの次元を変えても性能はほぼ変わらない」ということが分かる...
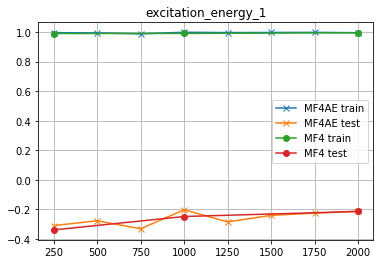
excitation_energy_1
何だこれはッ! ますます「使えねー」結果じゃねーかよッ!
コイツもかッ!!
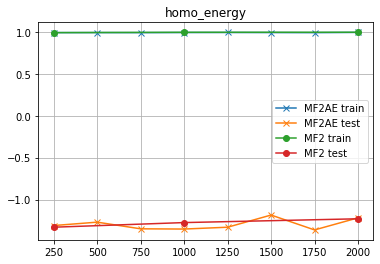
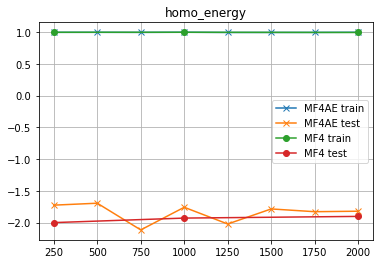
homo_energy
さらにダメになりやがったッ!!!!
さらに「悪い」ッ!! ふざけやがってクソがァァァーッ!!!
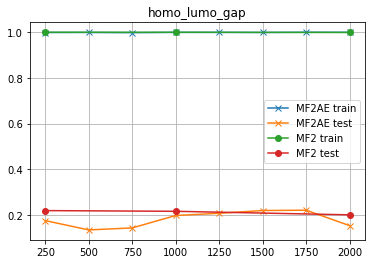
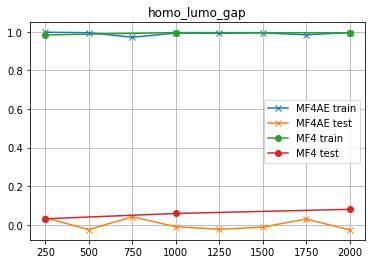
homo_lumo_gap
さっきよりは良くなったが...「使えねー」ことには変わりねーッ!
ドイツもコイツもッ!!! 「MF4はMF2より悪い」のかよッ!!!
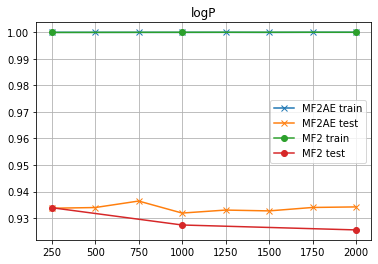
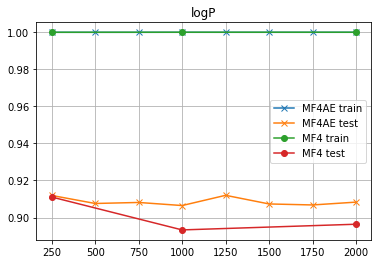
logP
ふぅ...このくらいの予測精度が出ると「安心」するぜ...
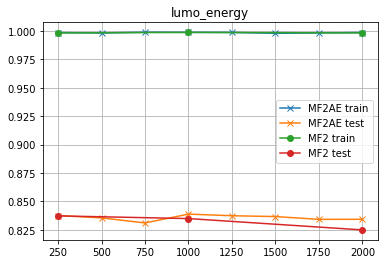
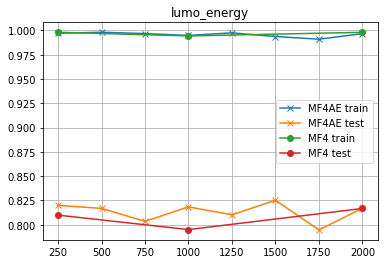
lumo_energy
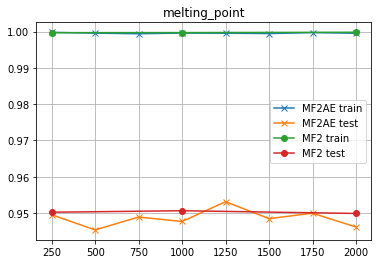
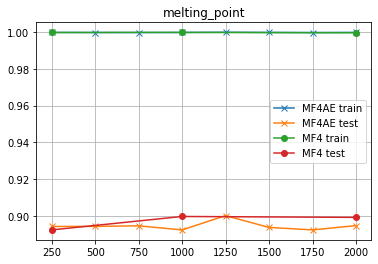
melting_point
molecular_refractivity
以上、見てきたことをまとめると、こうだ。
- MLPの隠れ層の次元を高くしすぎると精度が落ちることがある。
- オートエンコーダーを使って次元削減しても、予測性能はほぼ変わらない。
- オートエンコーダーの隠れ層の次元も、多くしたからといって精度が上がるわけじゃなさそうだ。
- MF4よりMF2のほうがテストデータの予測精度が高い。これは予測したい物性によるかも知れんが、少なくともPCCDBに記載してあるデータに関しては、全てそうだった。
計算時間
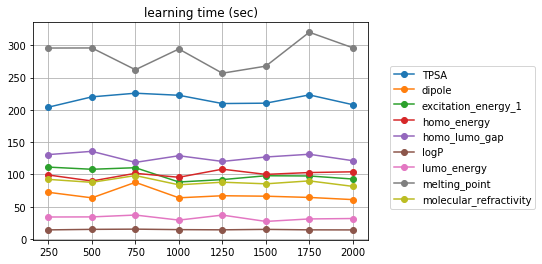
「オートエンコーダーで写像したベクトル」から物性を予測するMLPの学習時間は、こうだッ!
MF2AE: 20 〜 300 s くらいのオーダー
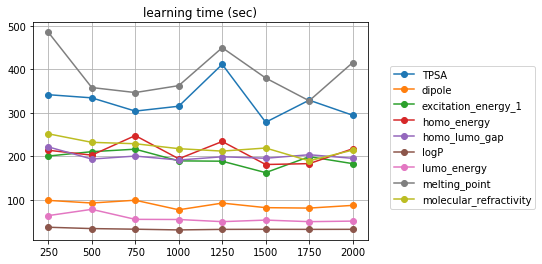
MF4AE: 40 〜 500 s くらいのオーダー
「隠れ層の次元に依存せず、学習時間はほぼ一定」???
...って驚くんじゃねェ...これは、横軸は「AEの隠れ層の次元」だ。つまり、MLP回帰するときの入力層の次元だ。「MLP回帰の隠れ層」の次元は 250 に固定してある。
「真の学習時間」はよォ...紛らわしいが「AEの学習時間+MLPの学習時間」になる...
AEを使う時は、物性の値を使わねェから、テメェの分子セットが決まっていれば、あらかじめ計算しておける...計算時間のオーダーは、
- MF2 の AE: 42.35 s
- MF4 の AE: 90.93 s
ってとこだ... つまり、「AEの学習時間+MLPの学習時間」は
- MF2AE なら 60〜340 s くらいのオーダー
- MF4AE なら 110〜580 s くらいのオーダー
だな...一方で、MFを直接使ったMLP回帰の学習時間は
- MF2 なら 20 〜 250 s くらいのオーダー
- MF4 なら 20 〜 400 s くらいのオーダー
...
ドドドドドドド....
...「負け」てるじゃねェかヨォォォォォッ!!!!!!
つまり、オレのこの解析はアァァァッ!!!
無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄アアァァァッ!!!!
→ TO BE CONTINUED...