問題
線型分離可能なデータ集合に対してロジスティック回帰モデルの最尤解が, クラスを分離する決定境界$\mathrm{w^T{\phi}(x)=0}$を満足するベクトル$\mathbf{w}$に対しその値を$\mathrm{\infty}$とすることで得られることを示せ.
ロジスティック回帰モデル
本文より
まず2クラス分類問題における一般化線形モデルを扱ってみよう. 4.2節での生成的アプローチの議論において,かなり一般的な仮定の下で.クラス C1 の事後確率が特徴ベクトル$\mathbf{\phi}$の線形関数のロジスティックシグモイド関数として書けた.つまりその事後確率は
$$
\mathrm{p(C_1|\phi)=y(\phi)=\sigma(w^T\phi)}
\tag{4.87}
$$
$$
\mathrm{p(C_2|\phi)=1-p(C_1|\phi)}
\tag{4.87.a}
$$
$$
\mathrm{\sigma(a)=\frac{1}{1+exp(-a)}}
\tag{4.59}
$$
となる$\mathrm{\sigma(\centerdot)}$は(4.59)で定義されるロジスティックシグモイド関数である.このモデルは回帰より分類のモデルであるが統計ではロジスティック回帰として知られている.
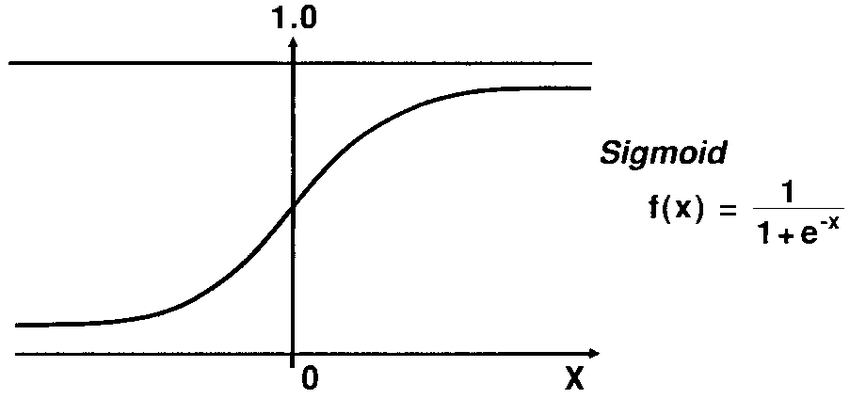
ロジスティックシグモイド関数
シグモイド関数は$\mathrm{0<f(x)<1, lim_{x\to-\infty}f(x)=0,lim_{x\to\infty}f(x)=1}$という性質を持つことから確率としてみることができる.また以下のように使うことで2クラス分類にも用いることができる.
\begin{align*}
\left\{
\begin{array}{ll}
y=1 \hspace{10pt} (f(x)\ge0.5, x\ge0) \\
y=0 \hspace{10pt} (f(x)<0.5, x<0)
\end{array}
\right.
\end{align*}
上の分類法より$\mathrm{x=0}$が分類の境界になっていることがわかる.この境界がロジスティック回帰による決定境界である.
方針
まずベクトル$\mathbf{w}$がクラスを分離する決定境界$\mathrm{w^T{\phi}(x)=0}$を満足することを示す.そして次に推定した最尤解のとる値によってベクトル$\mathrm{w}$がどのような値を取るのかを考え題意を示していく.
解答
線型分離可能なデータ集合{$\mathrm{\phi_n, t_n}$}, $\mathrm{t_n\in}$ {0,1}が存在するときに
\begin{align*}
\left\{
\begin{array}{ll}
t_n &=1 \hspace{10pt} (w^T{\phi}\ge0)\\
t_n &=0 \hspace{10pt} (w^T{\phi}<0) \hspace{10pt} ただし\phi = \phi(x)
\end{array}
\right.
\end{align*}
したがってベクトル$\mathbf{w}$はクラスを分離する決定境界$\mathrm{w^T{\phi}(x)=0}$を満足する.
次に最尤解について考える.最尤解を与える尤度関数は(4.89)で与えられる.
\begin{align*}
\mathrm{p(t|w)=\prod_{n=1}^Ny_n^{t_n}\bigl\{1-y_n\bigr\}^{1-t_n}}
\tag{4.89}
\end{align*}
$\mathrm{t=(t_1,...,t_n)^T}$であり$\mathrm{y_n=p(C_1|\phi_n)}$である.
尤度の負の対数を取って誤差関数を定義すると以下の(4.90)で与えられる交差エントロピー関数を得る.
\begin{align*}
\mathrm{E(w)}=\mathrm{-lnp(t|w)}=\mathrm{-\sum_{n=1}^N\bigl\{t_nlny_n+(1-t_n)ln(1-y_n)\bigr\}}
\tag{4.90}
\end{align*}
(4.90)より負の対数尤度は全ての$\mathrm{t_n}$に対して$\mathrm{y_n=t_n}$のときに最小化されることがわかる.与えられたデータ集合では$\mathrm{t_n=0, 1}$である.また$\mathrm{y_n}$が$\mathrm{y_n=0, 1}$を取りうる時、$\mathrm{w^T\phi}$の値は$\mathrm{\pm\infty}$である.したがってベクトル$\mathbf{w}$の値を$\mathrm{\infty}$とすることでロジスティック回帰モデルの最尤解が得られることが示された.