「信頼できる local score を作成する」 K-Fold クロスバリデーションの効果とは？

機械学習コンペティション（例: Kaggle）に参加していて、モデルづくりをしていると、

• 手元（train データ内）で計算したスコア（local score）
• コンペサイト上の public leaderboard のスコア

が全然一致せず、「どのモデルが本当に良いのか分からない」ということがよく起きます。

このとき重要になるのが、

「本番のスコアをある程度予測できる、信頼できる local score を作ること」

です。
本記事では、そのための基本テクニックである K-Fold クロスバリデーション について、

• そもそも何か
• どう書くか（コード例）
• 単純な 8:2 分割と比べて、どれくらい「信頼できる local score」になるか

を、できるだけ丁寧に説明します。

---

K-Fold クロスバリデーションとは？

まず、K-Fold クロスバリデーションに入る前に、「local score」と「単純な分割」の話から始めます。

local score とは何か

ここでは local score を次のように定義します。

自分の手元で、学習用データを分割して計算した評価値

具体的には、次のような流れです。

1. 訓練用のデータを train / validation に分ける（例: 8:2 に分割）
2. train でモデルを学習する
3. validation に対するスコア（正解率や RMSE など）を計算する
   → これを local score と呼ぶ

コンペなら、この local score を見ながら

• 特徴量を増やす・減らす
• ハイパーパラメータを変える
• モデルの種類を変える

といった試行錯誤を繰り返します。

なぜ単純な 1 回分割だとまずいのか

一番シンプルな方法は、次のような「1 回だけの train/validation 分割」です。

• 全データ 1000 行
• 800 行を train、200 行を validation にする（8:2 分割）
• train で学習し、validation のスコアを local score とする

一見これで良さそうですが、問題がいくつかあります。

1. 分割の仕方によってスコアが大きく変わる

   例えば、同じモデルでも、乱数シードを変えて分割し直すと、
   validation のスコアが 0.82 のときもあれば 0.87 のときもある、ということが普通に起きます。

2. 本番で出会うデータと validation の傾向が違うかもしれない

   • 偶然、validation 側に「判断しやすい」ケースばかり入ってしまった
   • 逆に「難しい」ケースばかり入ってしまった

   などの偏りがあると、

   • local score は高いのに本番スコアは低い
   • local score は低いのに本番スコアは高い
     といったことが起こりやすくなります。

3. validation に過剰に最適化しやすい

   1 回分の validation をずっと見ながらモデル調整をすると、
   「その分割の validation だけ」で良くなる方向に寄りがちです。
   つまり local score だけは高いのに、本番では再現しない 状態になります。

結果として、「local では良かったのに本番でダメだった」モデルが量産され、
local score への信頼度が下がります。

K-Fold クロスバリデーションの基本的な考え方

K-Fold クロスバリデーションは、この問題を和らげるために、

訓練データを K 個に分割し、
そのうち 1 つを検証用、残りを学習用として K 回繰り返す

という手順をとります。

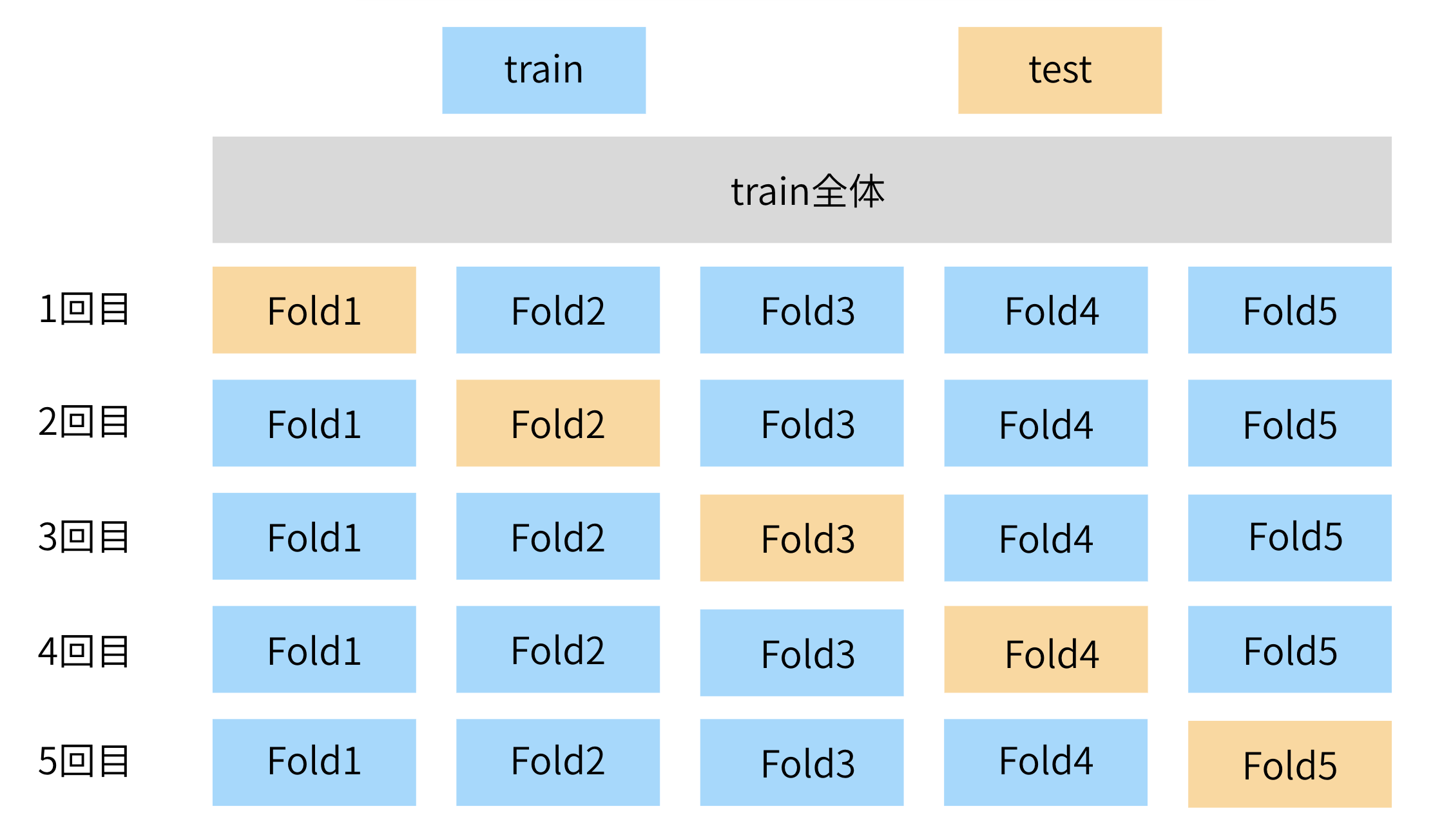
例として、K=5 の場合を説明します（5-Fold クロスバリデーション）。

1. 訓練用データ（例: 800 行）を、できるだけ均等に 5 分割する
   • fold 1, fold 2, fold 3, fold 4, fold 5
2. 1 回目
   • fold 2 〜 5 を学習用
   • fold 1 を検証用（validation）
3. 2 回目
   • fold 1,3,4,5 を学習用
   • fold 2 を検証用
4. 同様に、検証に使う fold を交代しながら、合計 5 回学習・評価する
5. 5 回の検証スコアを 1 つの指標にまとめるために、その「平均値」を local score として使う

こうすることで

• 検証に使われるデータが、1 回分割よりも多くなる
• 「たまたま有利な分割」「たまたま不利な分割」の影響を平均して抑えられる

ようになります。

信頼できる local score を作成するという観点

K-Fold クロスバリデーションを使うと、local score には次のような性質が出てきます。

• 1 回の分割だけを見る場合より、スコアのブレが小さくなる
• 乱数シードを変えても、local score の値が極端に変わりづらい
• 「local で良かったモデルが、本番でもそこそこ良い」ことが増える

つまり、

「local score が、モデルの本番データでの性能を、よりよく表している」

と言いやすくなります。
これが「信頼できる local score を作成する」ために、K-Fold がよく使われる理由です。

メリットとデメリットの整理

メリット

• スコアが安定しやすい
• 検証に使われるデータが増える（データを有効活用できる）
• 1 回だけの「当たり・外れ」分割の影響を平均でならせる
• Out-of-Fold（OOF）予測を作れる（後述）

デメリット・注意点

• 学習を K 回行うので、計算時間が約 K 倍かかる
• 時系列データなど、シャッフルしてはいけないデータでは注意
  • この場合は TimeSeriesSplit など専用の分割方法を使う
• 最終的な test データ（本番評価用）は、K-Fold に混ぜてはいけない
  • train の中だけで K-Fold を行い、test は最後の一回だけ使う

---

使用例

ここからは、実際のコードで K-Fold クロスバリデーションを使う例を示します。
どれも上から順に実行していけば動くようになっています。

1. cross_val_score を使った基本的な K-Fold

まずは、K-Fold クロスバリデーションを 自分で for ループを書かずに実行する方法 から見ていきます。

scikit-learn には cross_val_score という便利な関数があり、これを使うと

1. データを K 分割する
2. 各分割について「学習用データでモデルを学習 → 検証用データでスコアを計算」
3. K 回分のスコアをまとめて返す

という一連の流れを、自動で実行してくれます。

cross_val_score はざっくりいうと次のような関数です。

• 第1引数：学習させたいモデル（例: RandomForestClassifier のインスタンス）
• 第2引数：説明変数 X
• 第3引数：目的変数 y
• cv 引数：クロスバリデーションの分割方法
  • 整数（例: cv=5）を渡すと「単純に 5 分割」
  • KFold オブジェクトを渡すと、「シャッフルするか」「random_state は何か」などを細かく指定可能
• scoring 引数：評価指標（"accuracy", "roc_auc" など）

戻り値は「各 fold でのスコアが入った 1 次元配列」です。
この配列の平均値を取ることで、「K-Fold による local score」を簡単に得ることができます。

以下は、KFold オブジェクトを自分で用意して cross_val_score に渡す、基本的な例です。

# =========================
# 必要なライブラリのインポート
# =========================
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.model_selection import KFold, cross_val_score
from sklearn.ensemble import RandomForestClassifier

# =========================
# Titanic データの読み込み & 前処理
# =========================
# seaborn に同梱されている titanic データセットを使用
df = sns.load_dataset("titanic")

# 目的変数（生存フラグ: 0 or 1）
y = df["survived"].values

# 使用する特徴量の例
feature_cols = ["pclass", "sex", "age", "sibsp", "parch", "fare", "embarked"]

# 必要な列だけ抽出
df_feat = df[feature_cols].copy()

# カテゴリ列と数値列を分ける
cat_cols = ["sex", "embarked"]
num_cols = ["pclass", "age", "sibsp", "parch", "fare"]

# カテゴリ列を整数エンコード（カテゴリ → 0,1,2,... の整数に変換）
for col in cat_cols:
    df_feat[col] = df_feat[col].astype("category").cat.codes

# 数値列の欠損値を中央値で補完
for col in num_cols:
    df_feat[col] = df_feat[col].fillna(df_feat[col].median())

# 説明変数の ndarray
X = df_feat.values

# =========================
# モデルの定義
# =========================
model = RandomForestClassifier(
    n_estimators=200,  # 決定木の本数
    random_state=0,    # 再現性のための乱数シード
    n_jobs=-1,         # CPU をフル活用
)

# =========================
# K-Fold の設定
# =========================
kf = KFold(
    n_splits=5,        # 5 分割（5-Fold CV）
    shuffle=True,      # 分割前にシャッフルする
    random_state=0,    # 再現性のため固定
)

# =========================
# クロスバリデーションの実行
# =========================
scores = cross_val_score(
    model,
    X,
    y,
    cv=kf,
    scoring="accuracy",  # 評価指標（正解率）
)

print("fold ごとのスコア:", scores)
print(f"平均スコア (local score): {scores.mean():.3f}")
print(f"標準偏差: {scores.std():.3f}")

ここで出てくる

• fold ごとのスコア
• 平均スコア (local score)

が、K-Fold クロスバリデーションによる local score です。
標準偏差が小さいほど、「どの分割でもそこそこ同じスコアが出ている」ことを意味します。

2. OOF 予測を作る

次に、もう一歩進んで、OOF（Out-Of-Fold）予測を作る例です。

OOF 予測とは、

各行について、「その行を学習に使っていないモデルによる予測値」

のことです。
K-Fold をループで回しながら、検証用に回した部分の予測だけを集めることで作れます。

# =========================
# 必要なライブラリのインポート
# =========================
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# =========================
# データの準備（Titanic）
# =========================
# seaborn に同梱されている titanic データセットを読み込み
df = sns.load_dataset("titanic")

# 目的変数（生存フラグ: 0 or 1）
y = df["survived"].values

# 使用する特徴量の例
feature_cols = ["pclass", "sex", "age", "sibsp", "parch", "fare", "embarked"]

# 必要な列だけ抽出
df_feat = df[feature_cols].copy()

# カテゴリ列と数値列を分ける
cat_cols = ["sex", "embarked"]
num_cols = ["pclass", "age", "sibsp", "parch", "fare"]

# カテゴリ列を整数エンコード
for col in cat_cols:
    df_feat[col] = df_feat[col].astype("category").cat.codes

# 数値列の欠損値を中央値で補完
for col in num_cols:
    df_feat[col] = df_feat[col].fillna(df_feat[col].median())

# 説明変数の ndarray
X = df_feat.values

# =========================
# K-Fold の設定
# =========================
kf = KFold(
    n_splits=5,
    shuffle=True,
    random_state=0,
)

# =========================
# モデルの定義
# =========================
model = RandomForestClassifier(
    n_estimators=200,
    random_state=0,
    n_jobs=-1,
)

# =========================
# OOF 予測用の配列を用意
# =========================
# 各サンプルについて「そのサンプルを学習に使っていないモデルの予測確率」を格納する
oof_pred = np.zeros_like(y, dtype=float)

# 各 fold のスコア（validation スコア）を保存するリスト
oof_score_list = []

# =========================
# K-Fold で学習・予測
# =========================
for fold, (tr_idx, val_idx) in enumerate(kf.split(X, y), start=1):
    X_tr, X_val = X[tr_idx], X[val_idx]
    y_tr, y_val = y[tr_idx], y[val_idx]
    
    # 学習
    model.fit(X_tr, y_tr)
    
    # 検証データに対する予測（クラス1の確率）
    pred_val = model.predict_proba(X_val)[:, 1]
    
    # OOF 予測に格納（val_idx に対応する位置に入れる）
    oof_pred[val_idx] = pred_val
    
    # 0.5 を閾値にしてラベルに変換し、正解率を計算
    pred_val_label = (pred_val >= 0.5).astype(int)
    score = accuracy_score(y_val, pred_val_label)
    oof_score_list.append(score)
    
    print(f"fold {fold} のスコア: {score:.4f}")

print("fold ごとのスコア:", oof_score_list)
print(f"平均スコア (local score): {float(np.mean(oof_score_list)):.3f}")

oof_pred に入っている値は、各行に対して「その行を学習に使っていないモデル」が出した確率になっています。
この OOF 予測は、単にスコア計算に使うだけでなく、次のような応用ができます。

• メタモデルの学習（スタッキング）

  スタッキングでは、
  1段目：いくつかの異なるモデル（例: ランダムフォレスト、ロジスティック回帰、XGBoost など）を学習
  2段目：それらのモデルが出した予測値を「入力特徴量」として、別のモデル（メタモデル）を学習
  という構成をとります。

  このとき、2段目の学習に使う特徴量として「OOF 予測」を使うと、

  • 各行について「その行を学習に使っていないモデルの予測」を渡せる
  • 1段目モデルの「本番に近い予測性能」をメタモデルに渡せる

  という性質を保てます。
  逆に、単純に「学習に使ったデータに対する予測値」をそのまま使ってしまうと、
  1段目モデルが過学習している部分まで含めてメタモデルに渡してしまい、
  クロスバリデーションや本番に対する再現性が下がりやすくなります。

• 外れ値検出

  OOF 予測と実際の正解ラベルとの差を見て、

  • （今回のように単一モデルの場合）そのモデルが「高確率でクラス 1」と予測しているのに、実ラベルは 0
  • 逆に、「高確率でクラス 0」と予測しているのに、実ラベルは 1

といった行を「モデルから見て説明しづらいサンプル」として検出できます。
もし複数モデルを学習していれば、「多くのモデルが高確率で 1 と予測しているのにラベルは 0」のようなケースも同じように見つけられます。

こういった行は、

• ラベルの誤り（アノテーションミス）
• 入力特徴量の入力ミス
• そもそも分布的にかなり特殊なサンプル

である可能性があり、個別に確認・除外・重み調整などを検討するきっかけになります。

このように、OOF 予測は

• 「より正直な」モデルの出力（学習に使っていないデータに対する予測）
• 各サンプルごとに 1 つずつ割り当てられる値

という性質があるため、スタッキングや外れ値検出をはじめ、
モデル診断やアンサンブルの設計において重要な役割を果たします。

---

効果検証

ここでは、次の 2 つの方法を比較し、

• 方法 A: 単純な 8:2 分割での local score
• 方法 B: K-Fold クロスバリデーションの local score

それぞれが

test データ（本番に見立てたデータ）でのスコアと、どれくらい相関しているか

をテストします。

相関が高いほど、

local score が高いモデルほど、本番スコアも高い

と言いやすくなります。
つまり、「信頼できる local score」と言えます。

実験の手順

1. 全データを train / test に分ける（ここは一度決めたら固定）
   • test は「本番データの代わり」と考える
2. いくつかのハイパーパラメータの組み合わせ（例: 20 通り）について
   • 方法 A: train をさらに 8:2 に分割し、そのパラメータで学習して local score と test score を計算
   • 方法 B: 同じパラメータで train に対して K-Fold を行い、local score と test score を計算
3. 方法 A / B それぞれについて
   • 「local score のリスト」と「test score のリスト」の相関係数（ピアソン相関）を計算する
4. 方法 A と方法 B の相関係数を比べ、どちらが「本番スコアを良く予測しているか」を見る

ここで変えているのは乱数ではなく、**ハイパーパラメータの候補（モデル設定）**です。
実務で複数の特徴量やパラメータを比較するときの状況に近いと考えられます。

実験コード

ここからの実験でも、先ほどと同じく、seaborn に同梱されている Titanic データセット（sns.load_dataset("titanic")）を使います。

# =========================
# 必要なライブラリのインポート
# =========================
import numpy as np
import pandas as pd
import seaborn as sns

from sklearn.model_selection import train_test_split, KFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from tqdm import tqdm

# =========================
# 1. Titanic データを読み込み & 前処理
# =========================
titanic = sns.load_dataset("titanic")

# 使う列を選択
use_cols = ["survived", "pclass", "sex", "age", "sibsp", "parch", "fare", "embarked"]
df = titanic[use_cols].copy()

# 欠損行を削除（シンプルな方法）
df = df.dropna()

# 目的変数と説明変数に分割
y_all = df["survived"].astype(int).values  # 0 or 1
# カテゴリ列をダミー変数に変換
X_all = pd.get_dummies(df.drop("survived", axis=1), drop_first=True).values

# train/test に分割（ここは一度決めたら固定）
X_train_all, X_test, y_train_all, y_test = train_test_split(
    X_all,
    y_all,
    test_size=0.2,      # 8:2 に分割
    random_state=42,    # 再現性のため固定
    stratify=y_all,     # クラスの比率が偏らないようにする
)

# =========================
# 2. ハイパーパラメータ 20 通りを用意
# =========================
param_list = []
for max_depth in [3, 5, 7, None]:
    for min_samples_leaf in [4, 8, 16, 32, 64]:
        param_list.append(
            {
                "max_depth": max_depth,
                "min_samples_leaf": min_samples_leaf,
            }
        )
# len(param_list) == 4 * 5 = 20

# =========================
# 方法 A: 単純 8:2 split の評価関数
# =========================
def evaluate_with_simple_split(params: dict):
    """
    方法 A:
    train_all をさらに 8:2 に分割し、
    その validation スコアを local score とする。
    ハイパーパラメータは params を使用。
    """
    X_tr, X_val, y_tr, y_val = train_test_split(
        X_train_all,
        y_train_all,
        test_size=0.2,      # train_all の中で 8:2 に分割
        random_state=0,     # 分割は固定（パラメータ比較のため）
        stratify=y_train_all,
    )
    
    model = RandomForestClassifier(
        n_estimators=200,
        random_state=0,   # モデル側の乱数も固定
        n_jobs=-1,
        **params,
    )
    model.fit(X_tr, y_tr)
    
    # local score（validation スコア）
    val_pred = model.predict(X_val)
    local_score = accuracy_score(y_val, val_pred)
    
    # test データに対するスコア
    test_pred = model.predict(X_test)
    test_score = accuracy_score(y_test, test_pred)
    
    return local_score, test_score

# =========================
# 方法 B: K-Fold CV の評価関数
# =========================
def evaluate_with_kfold(params: dict, n_splits: int = 5):
    """
    方法 B:
    train_all に KFold を適用し、
    fold ごとのスコアの平均を local score とする。
    test 側は、各 fold のモデルの予測を平均してスコアを計算する。
    ハイパーパラメータは params を使用。
    """
    kf = KFold(
        n_splits=n_splits,
        shuffle=True,
        random_state=42,  # 全パラメータで同じ fold 分割を共有
    )
    
    oof_scores = []   # fold ごとの validation スコア
    test_preds = []   # test 用確率予測を各 fold ごとに保存

    for tr_idx, val_idx in kf.split(X_train_all, y_train_all):
        X_tr, X_val = X_train_all[tr_idx], X_train_all[val_idx]
        y_tr, y_val = y_train_all[tr_idx], y_train_all[val_idx]
        
        model = RandomForestClassifier(
            n_estimators=200,
            random_state=0,
            n_jobs=-1,
            **params,
        )
        model.fit(X_tr, y_tr)
        
        # fold ごとの local score
        val_pred = model.predict(X_val)
        oof_scores.append(accuracy_score(y_val, val_pred))
        
        # test に対する予測（クラス1の確率）
        test_pred = model.predict_proba(X_test)[:, 1]
        test_preds.append(test_pred)
    
    # local score は fold ごとのスコアの平均
    local_score = float(np.mean(oof_scores))
    
    # test 側は fold ごとの確率を平均し、0.5 でラベル化してスコア計算
    test_mean_prob = np.mean(test_preds, axis=0)
    test_pred_label = (test_mean_prob >= 0.5).astype(int)
    test_score = accuracy_score(y_test, test_pred_label)
    
    return local_score, test_score

# =========================
# 3. パラメータ 20 通りでシミュレーション
# =========================
simple_local_list = []
simple_test_list = []
kfold_local_list = []
kfold_test_list = []

for params in tqdm(param_list, desc="Param sets"):
    # 方法 A: 単純 8:2 split
    local_a, test_a = evaluate_with_simple_split(params)
    simple_local_list.append(local_a)
    simple_test_list.append(test_a)
    
    # 方法 B: KFold CV
    local_b, test_b = evaluate_with_kfold(params)
    kfold_local_list.append(local_b)
    kfold_test_list.append(test_b)

print()  # tqdm の進捗バーと出力を区切るための改行

# =========================
# 4. 相関係数（ピアソン相関）を計算
# =========================
def pearson_corr(x, y):
    x = np.array(x)
    y = np.array(y)
    return np.corrcoef(x, y)[0, 1]

corr_simple = pearson_corr(simple_local_list, simple_test_list)
corr_kfold = pearson_corr(kfold_local_list, kfold_test_list)

print(f"方法 A (単純 8:2 split) の local と test の相関: {corr_simple:.3f}")
print(f"方法 B (KFold CV)       の local と test の相関: {corr_kfold:.3f}")

実行すると、環境にもよりますが、

• 方法 A（単純 8:2）の相関より
• 方法 B（K-Fold）の相関のほうが高くなる（または少なくとも同程度）

という結果になることがよくあります。

今回の実験環境（Titanic データセット・20 通りのハイパーパラメータ）では、例えば次のような結果になりました。
（相関係数は小数第 4 位を四捨五入しています。）

方法	説明	local と test の相関
方法 A	単純 8:2 split	0.627
方法 B	K-Fold クロスバリデーション	0.796

つまり、

K-Fold クロスバリデーションで作った local score のほうが、
test（本番に近いデータ）での性能をよりよく反映している

と言いやすくなります。
この意味で、**K-Fold は「信頼できる local score を作成するための標準的な方法」**と考えられます。

---

まとめ

local score は「手元で計算する評価値」であり、モデル同士を比較するときの重要な指標です。ただし、単純に 1 回だけ train/validation を 8:2 に分割して評価すると、分割のしかた（運）にスコアが左右されやすく、本番データのスコアをうまく予測できないことがよくあります。

この問題を和らげるのが K-Fold クロスバリデーションです。データを K 分割して複数回学習・評価し、その結果を平均することで、1 回分割に比べてスコアのブレを小さくできます。実験でも、単純な 8:2 split より K-Fold のほうが、local score と test スコアの相関が高くなり、「local で良いモデルが本番でも良い」傾向が強くなることが確認できました。

さらに、K-Fold の過程で得られる OOF 予測は、スタッキング用の入力や外れ値検出などにも利用できます。どのようなデータで予測を外しやすいかを調べることもできるので、モデルを見直すときの手がかりになります。

実務やコンペでは、train データの中で K-Fold による local score を基準にモデル選択・改善を行うという流れを徹底することで、本番スコアをある程度予測できる、信頼できる local score を作りやすくなります。