- AIでデータ分析-定常性の判定:季節性非定常データの視覚的判定
- 用いるデータの紹介
- AIの活用:時系列データをプロットしたグラフ・コレログラム・偏コレログラムを作成し定常性の判定を視覚的に行う
- まとめ
AIでデータ分析-定常性の判定:季節性非定常データの視覚的判定
このノートは、データ分析においてAIを使って何ができて何ができないかを検証するために、実際に試した結果をまとめたノートです。
今回はトレンド非定常データに対しAIを用いてグラフを作成し、定常性の判定を視覚的に行ってみたいと思います。
AIを用いることでいかに効率化できるのか、体験していただければと思います。
所要時間は10分ほどとなっています。
それでは、さっそく始めていきましょう!
データの紹介
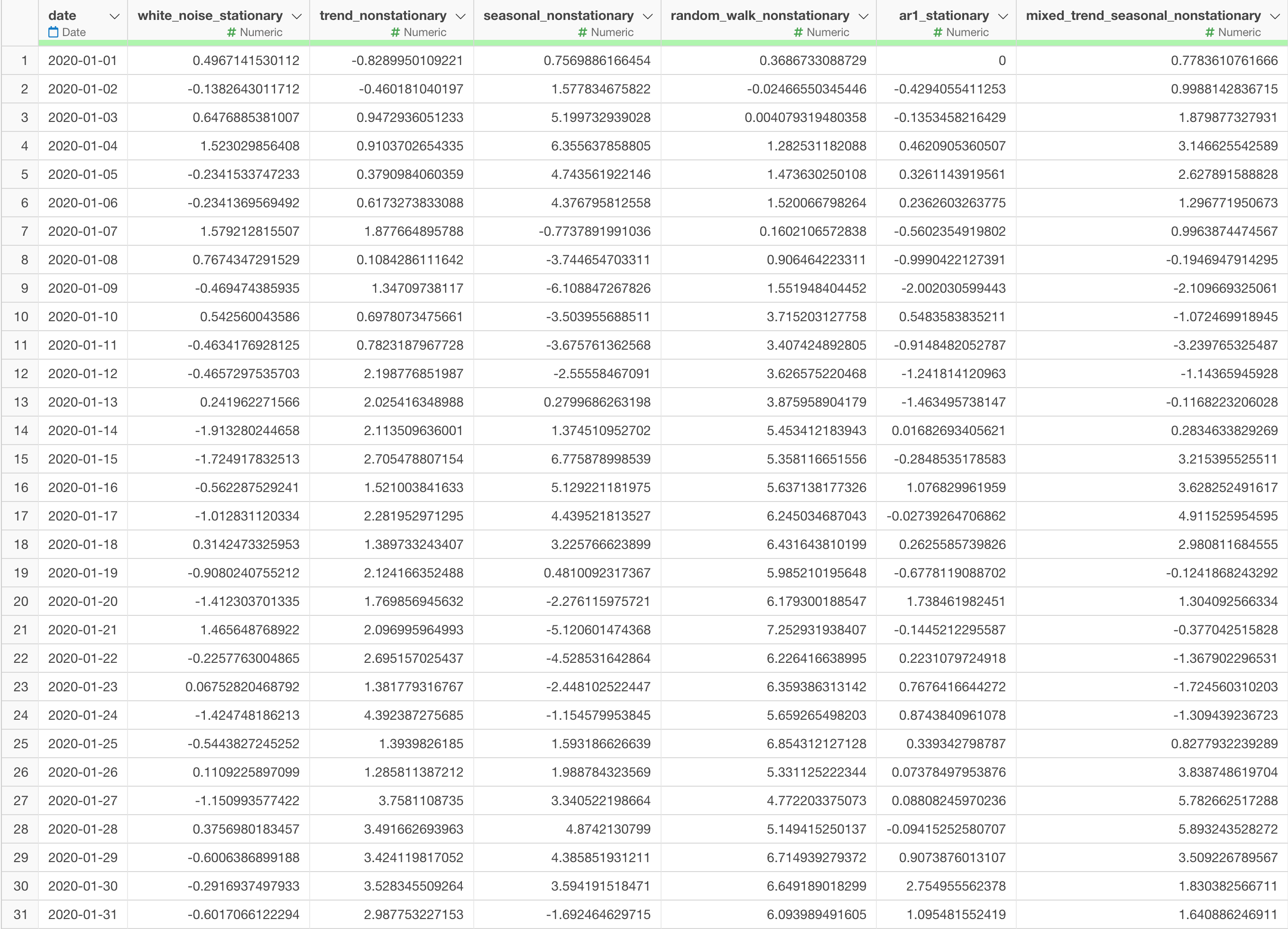
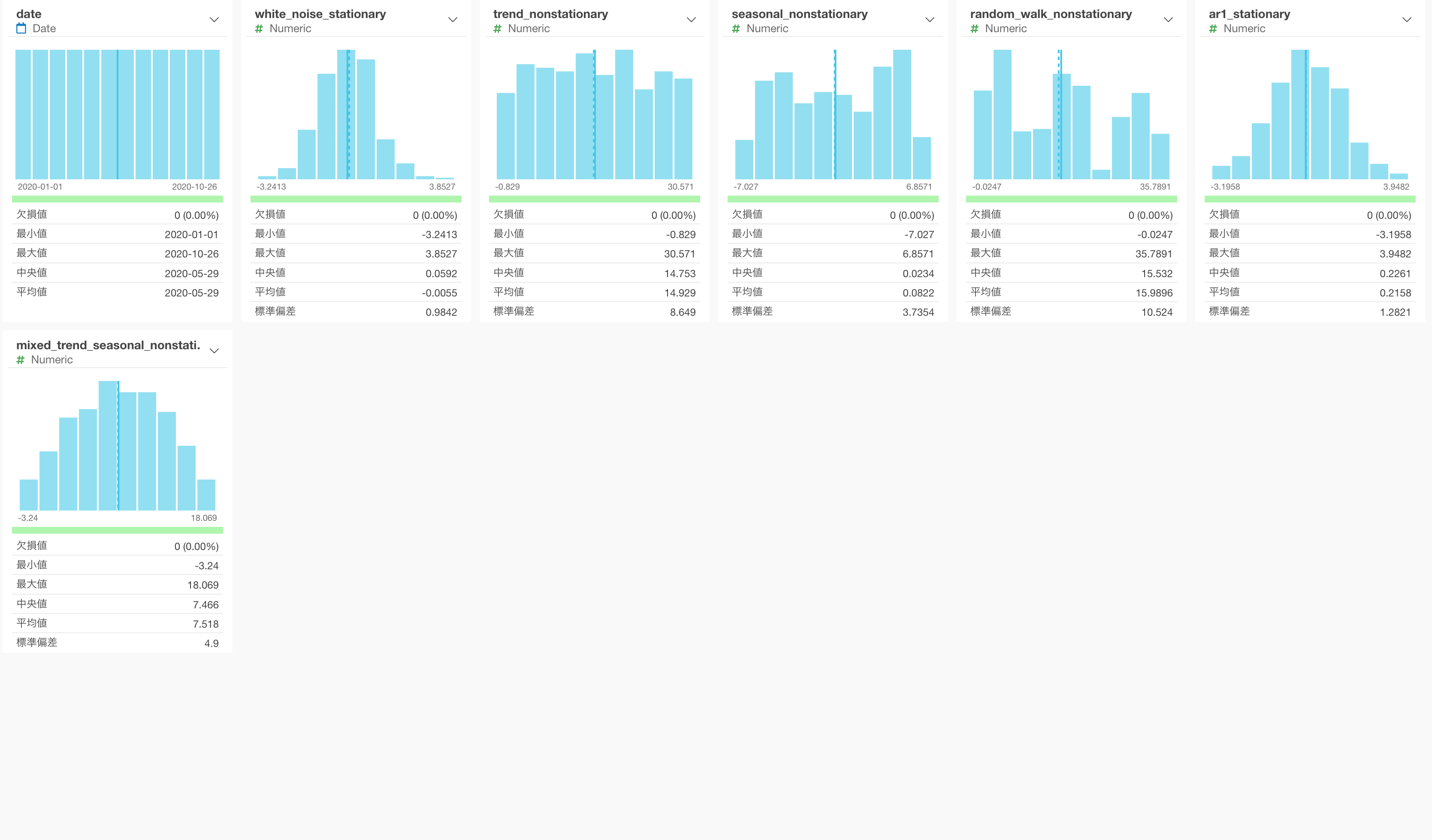
今回検証で得られたデータはsynthetic_time_series_for_stationarityです。
サンプルデータはこちらからダウンロードできます。
1行が1日のデータになっています。
AIの活用:時系列データをプロットしたグラフ・コレログラム・偏コレログラムを作成し定常性の判定を視覚的に行う
結果を確認します。
定常な時系列データとは二次統計量(平均・分散・自己共分散)が時間によって変化しない時系列データのことでした。
時系列データのプロットからの判定
見るポイント
・トレンドの有無:データが全体的に上昇または下降傾向を示しているか
・分散の均一性:時間と共にデータのばらつき(変動幅)が変化していないか
・周期性(季節性)の有無:明らかな繰り返しパターン(周期的な上昇・下降)が見られるか
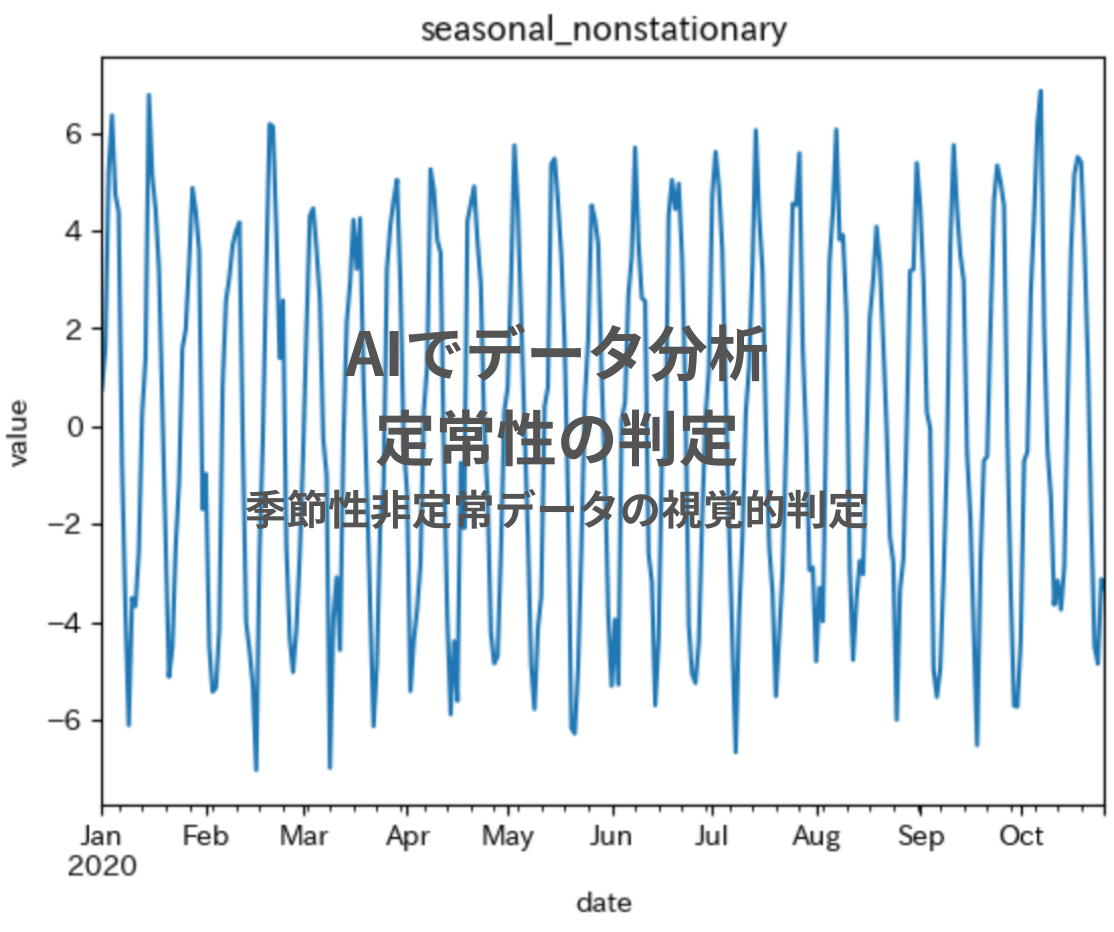
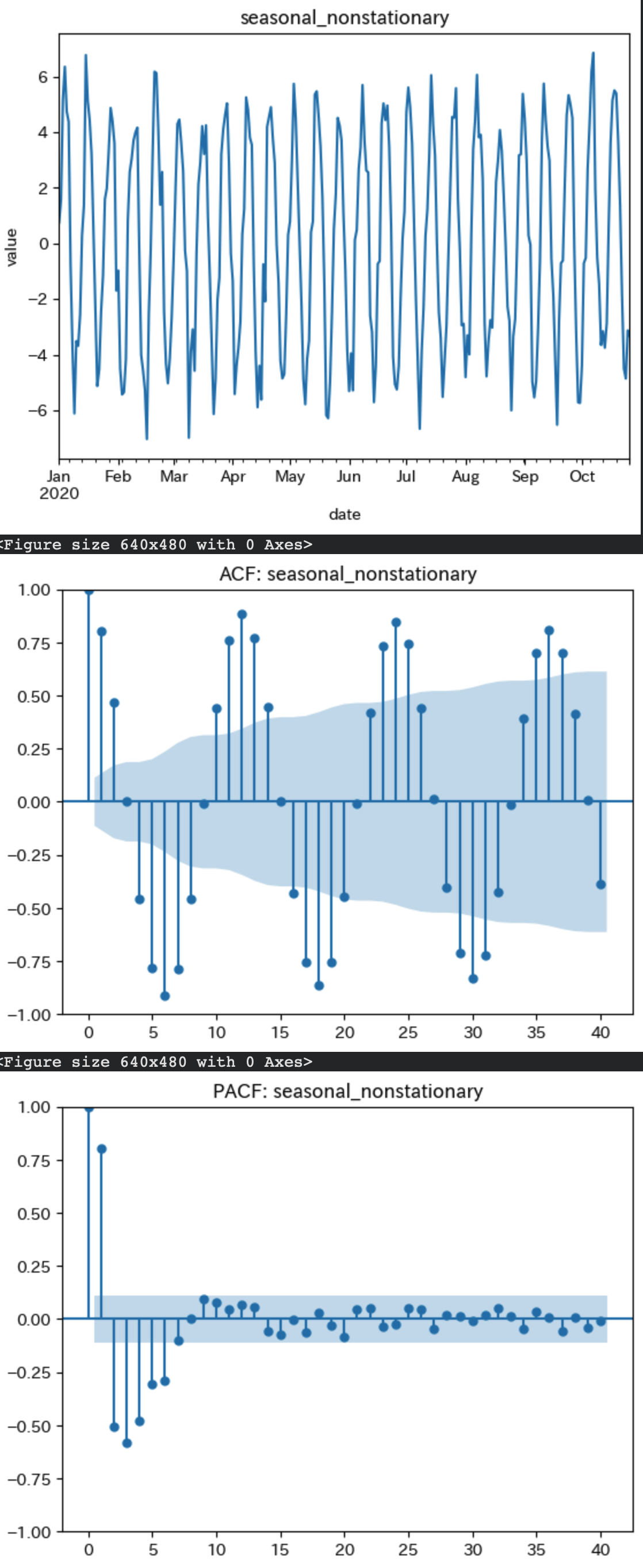
時系列データをプロットしたグラフを見ると、一定の間隔で値が上がったり下がったりを繰り返す波のようなパターンが見られ、季節性が確認されます。非定常データだと判定できそうです。
ACF(自己相関関数)プロットからの判定
見るポイント
・減衰の速さ:自己相関係数の棒が、ラグが増えるにつれてどれくらいの速さでゼロ(信頼区間内)に収まるか。
・周期的なスパイク:特定のラグ(季節周期に対応するラグ)で、繰り返し有意な(信頼区間を超える)相関が見られるか。
コレログラムを見ると、6日周期でACFがゆっくりと減衰しており、多くのラグで高い自己相関が確認できます。これは過去の遠い値が現在の値に対し長期的に影響を与え続けていることを示しています。
トレンドがあると、過去の遠い時点t-k(kはラグ)と現在の時点tの値の間には、そのトレンドに沿った長期的な依存関係が生まれます。
結果として、自己共分散がラグkだけでなく、時点tそのものに依存することになり、時間によって自己共分散構造が変化します。
そのため定常性の定義に沿わないことが分かり、これは非定常データであると判定できます。
PACF(偏自己相関関数)プロットからの判定
見るポイント
・初期の減衰:最初の数ラグで有意な値を示した後、残りのラグで突然ゼロに落ち込む(信頼区間内に入る)か。
・季節周期でのスパイク:ACFと同様に、季節周期に対応するラグでスパイクが見られるか。
偏コレログラムでは、ラグ1が極めて大きく、これは非定常系列(単位根・季節単位根)に典型的に見られる特徴です。
一方で、ラグ7まで有意な偏自己相関が見られ、それ以降は信頼区間内に収まっているため、形だけ見れば AR(7) 過程に似ています。しかし、非定常系列でも PACF が有限ラグで切れたような形状を示すことは多いため、PACF の形だけでは定常性を判定することはできなさそうです
したがって、この PACF から「定常性がある」と結論付けることはできさそうですが
時系列のプロット・ACFも踏まえると季節性非定常データであると判定できそうです。
AIを用いて視覚的に正しく定常性の判定を行うことができました。
まとめ
今回は季節性非定常データに対し、AIを用いて視覚的に定常性の判定を正しく行えるのか試しました。
結果はAIを用いて視覚的にも正しく定常性の判定を行えることを確認することができました。
AIでできることとできないことを把握し、うまく活用することで、データ分析もかなり効率化できそうですね!
AIでデータ分析-定常性の判定:季節性非定常データの視覚的判定 は以上となります!