- AIでデータ分析-時系列モデルの同定
- 用いるデータの紹介
- Pythonで時系列データの可視化・コレログラム/偏コレログラムを作成し、データがARMA(2,3)に当てはまっているか確認する
- AIの活用:コレログラム/偏コレログラムの画像情報をchatGPTに与えモデルを同定する
- まとめ
AIでデータ分析-定常性の判定:季節性非定常データの視覚的判定
このノートは、データ分析においてAIを使って何ができて何ができないかを検証するために、実際に試した結果をまとめたノートです。
今回はトレンド非定常データに対しAIを用いてグラフを作成し、定常性の判定を視覚的に行ってみたいと思います。
AIを用いることでいかに効率化できるのか、体験していただければと思います。
所要時間は10分ほどとなっています。
それでは、さっそく始めていきましょう!
データの紹介
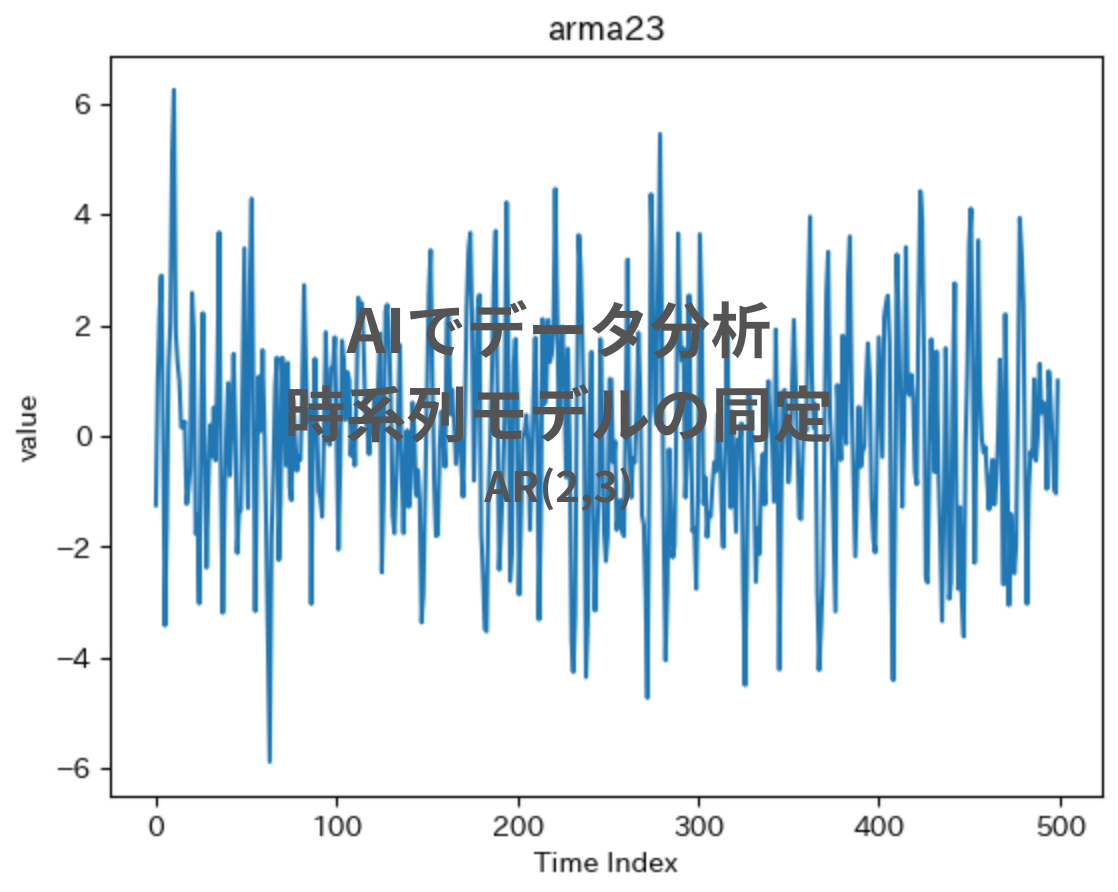
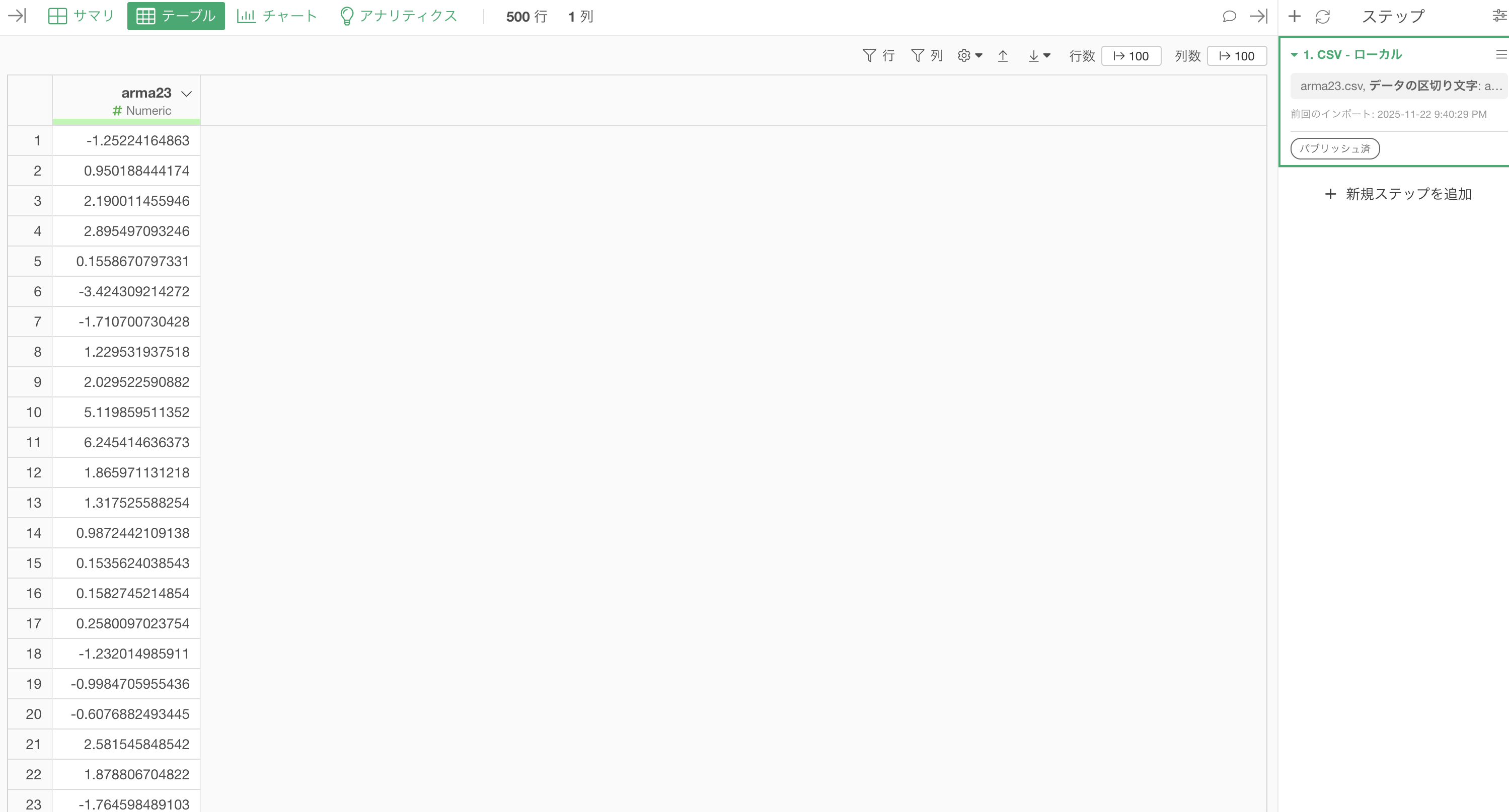
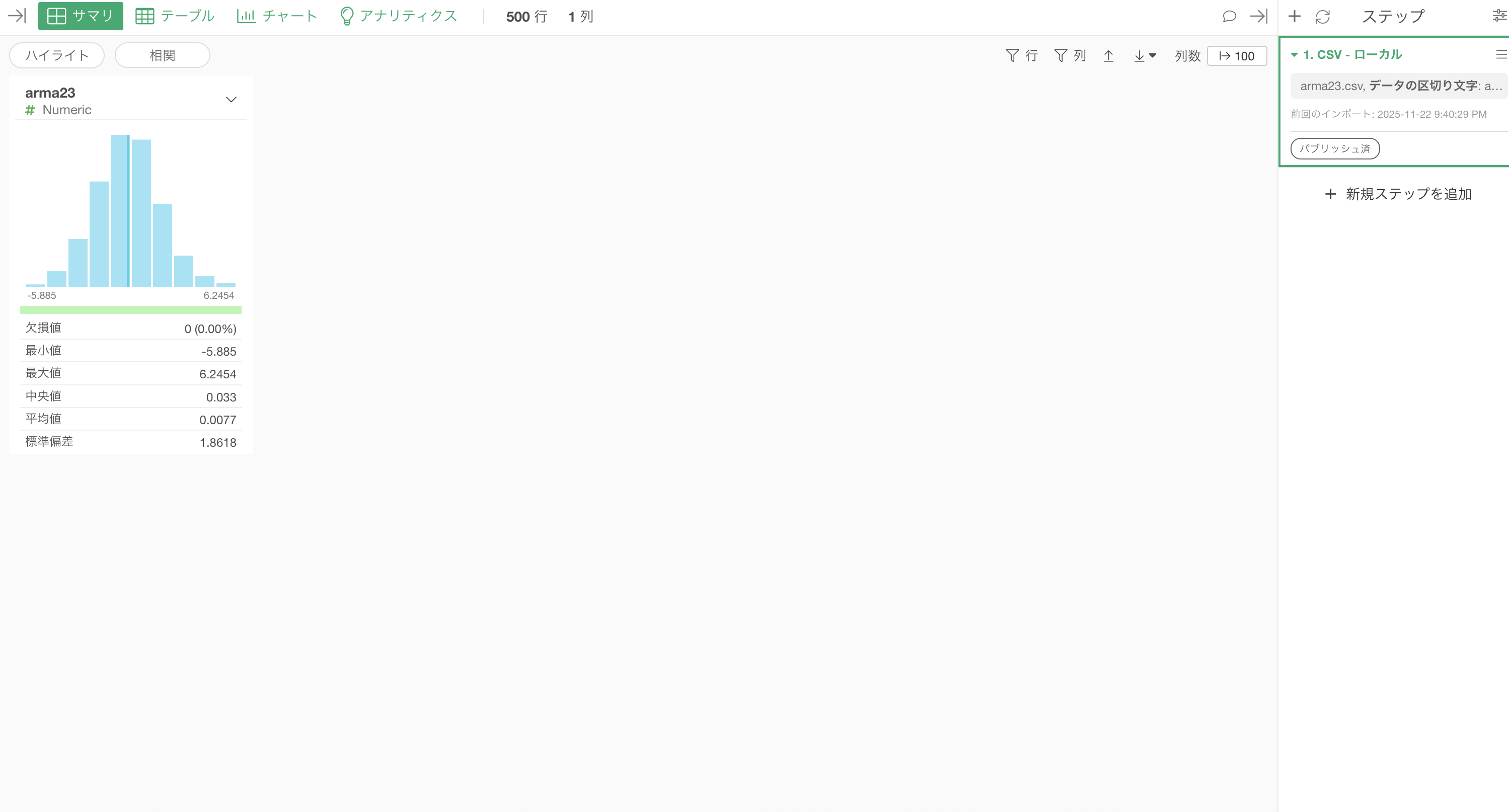
今回検証で得られたデータはAIで生成したarma23です。
サンプルデータはこちらからダウンロードできます。
1行が1つの値を示す時系列データになっています。
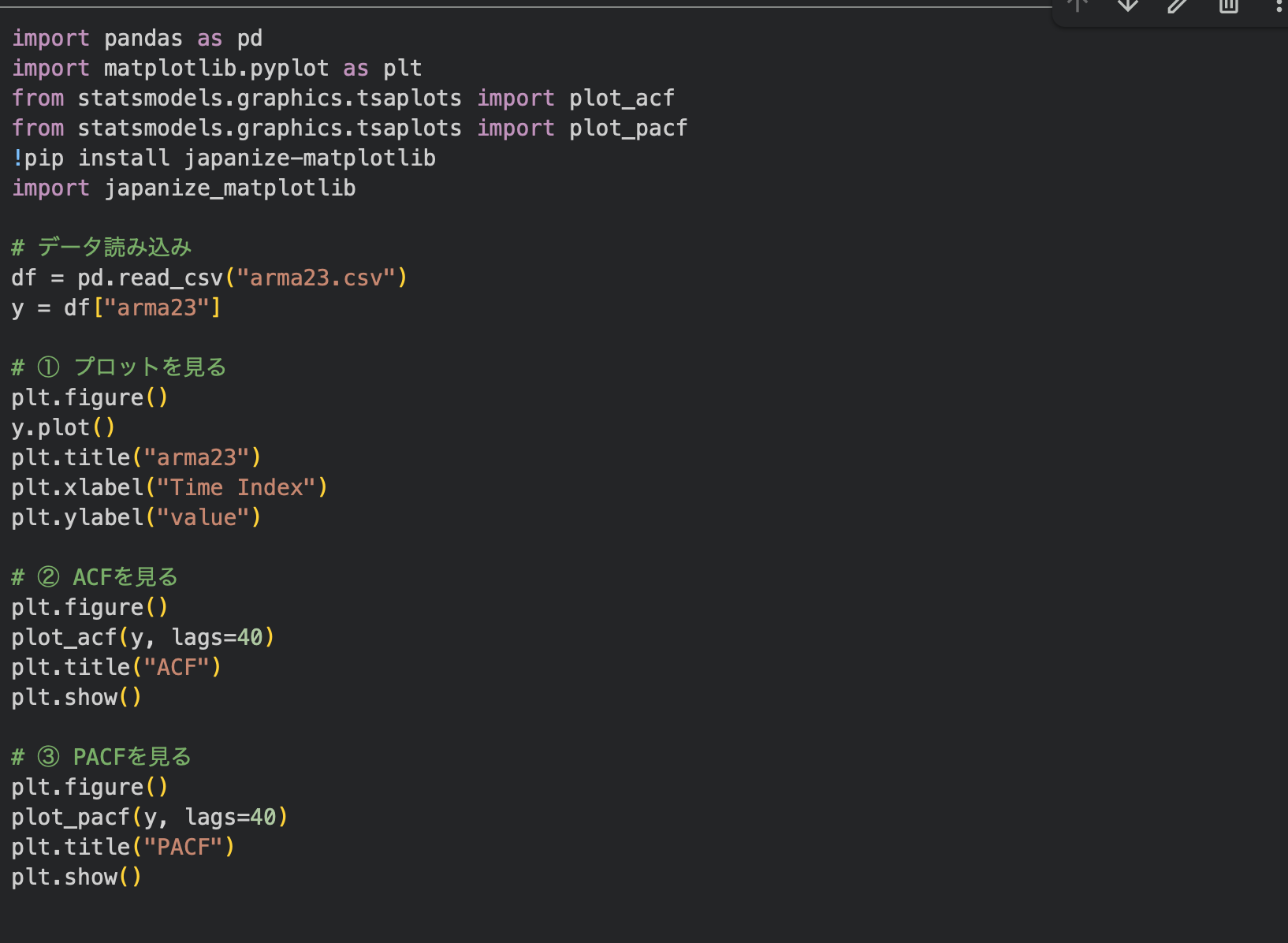
Pythonで時系列データの可視化・コレログラム/偏コレログラムを作成し、データがARMA(2,3)に当てはまっているか確認する
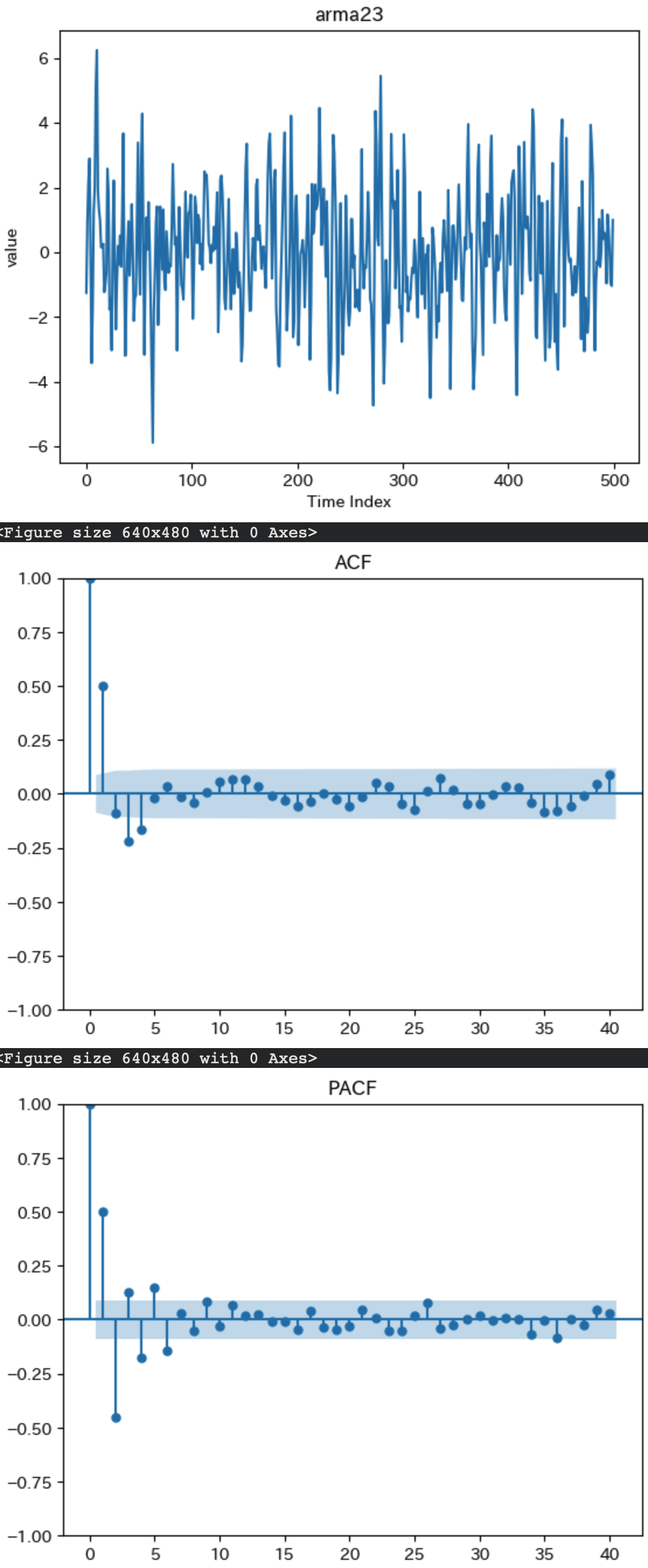
結果を確認します。
ACFの考察
ACFを見るとラグ3まで大きな相関が見られ、ラグ4以降ではゼロ付近に向かって減衰しています。これは一見すると MA(3) の特徴と似ています。
理論的な MA(q) モデルでは、ε の有限依存でモデルが構成されており、ACF は「現在の誤差 ε と、どのラグまで誤差を共有しているか」を表します。そのため、母集団の ACF はラグ q で 0 となり、それ以降は 0 になります。しかし今回の標本 ACF では、ラグ3を超えても系統的な減衰が続いており、「q でパタッと切れる」という MA(q) の特徴が見られません。
一方、ARMA(p,q) では現在の Xt は「過去の X」と「過去の ε」の両方の線形結合で表されるため、AR 部分による間接効果が無限に連鎖し、ACF は一般に「切れずに減衰」します。
したがって、ACF からは純粋な MA(3) よりも ARMA(p,3) の方が適切だと考えられます。
PACFの考察
続いてPACFを見るとラグ2まで大きな相関を示し、それ以降は急激に小さくなり減衰しています。これは AR(2) の特徴と似ています。
理論的な AR(p) モデルでは、PACF は「ラグ k の Xt−kが、ラグ1〜k−1の X の影響を取り除いたうえで、 Xtに与える直接的な影響」を表すため、ラグ p までがゼロにならず、それより大きなラグでは理論上 0 になります。しかし今回の 標本PACF では、ラグ2以降も小さいながら有意なスパイクが残り、完全には「pで切れる」形にはなっていません。
一方、ARMA(p,q) では MA(q) 部分が AR∞ に展開されるため、過去の X からの直接的な影響はラグが大きくなるにつれて減衰はするものの、理論的には無限に続きます。この性質が PACF の切れずに減衰する形で現れます。
したがって、PACF を踏まえると純粋な AR(2) よりも ARMA(2,q) の方が適切だと考えられます。
考察結果
ACF からは MA(3) 成分が、PACF からは AR(2) 成分が示唆され、いずれも「純粋な AR だけ/MA だけ」では説明しきれない減衰パターンを持っています。このため、ACF・PACF の両方を総合すると、使用した時系列データを表す時系列モデルとして ARMA(2,3) を同定するのが最も自然であると判断できます。
所要時間は10分でした。
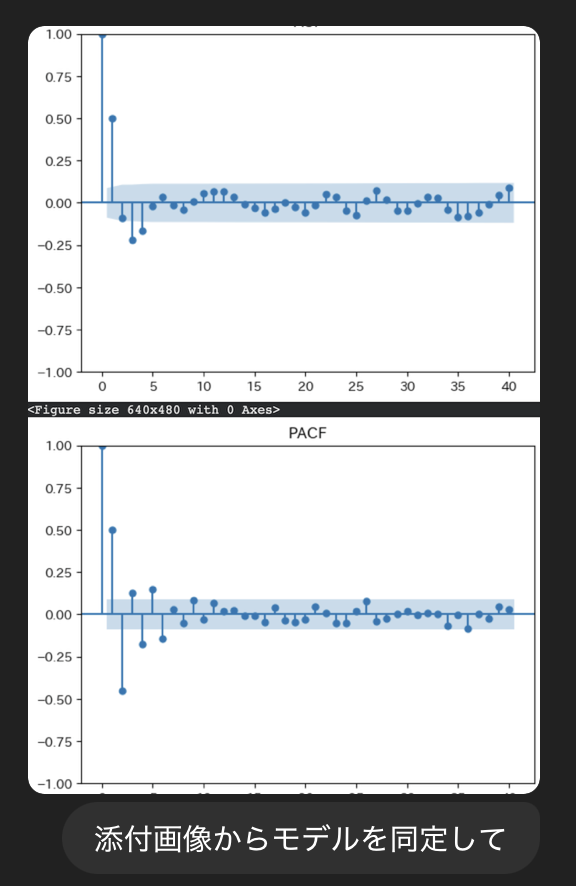
AIの活用:時系列データをプロットしたグラフ・コレログラム・偏コレログラムを作成し定常性の判定を視覚的に行う
結果を確認します。
ARMA(2,3)とモデルが同定されており、AIを用いて正しく時系列モデルの同定を行うことができました。
所要時間は3分でした。
まとめ
今回はARMA(2,3)に当てはまるデータに対し、AIを用いて正しくモデルの同定が行えるのか試しました。
結果はAIを用いて正しく時系列モデルの同定を行えることを確認することができました。
AIでできることとできないことを把握し、うまく活用することで、データ分析もかなり効率化できそうですね!
AIでデータ分析-時系列モデルの同定 は以上となります!