はじめに
ICCV2019から3D の人の形を推定する以下の論文
S. Saito, et. al. "PIFuHD: Multi-Level Pixel-Aligned Implicit Function for High-Resolution 3D Human Digitization"
のまとめ
ちなみに同じサイトーさんから既に
[2]PIFuHD: Multi-Level Pixel-Aligned Implicit Function for High-Resolution 3D Human Digitization
が発表されてて、CVPR2020にacceptされてるらしい。
arXiv:
https://arxiv.org/abs/1905.05172
著者のコード:
https://github.com/shunsukesaito/PIFu
Pytorchで実装されてる。
まとめ
- 服を着た人の画像を入力して、その3次元形状やテクスチャを推定するモデル
- PIFu(Pixel-aligned implicit function)を使い end-to-end で学習する
- これまでの3d 形状推定と比べて精度・及びメモリ使用量で優れる
以下が推論の例。
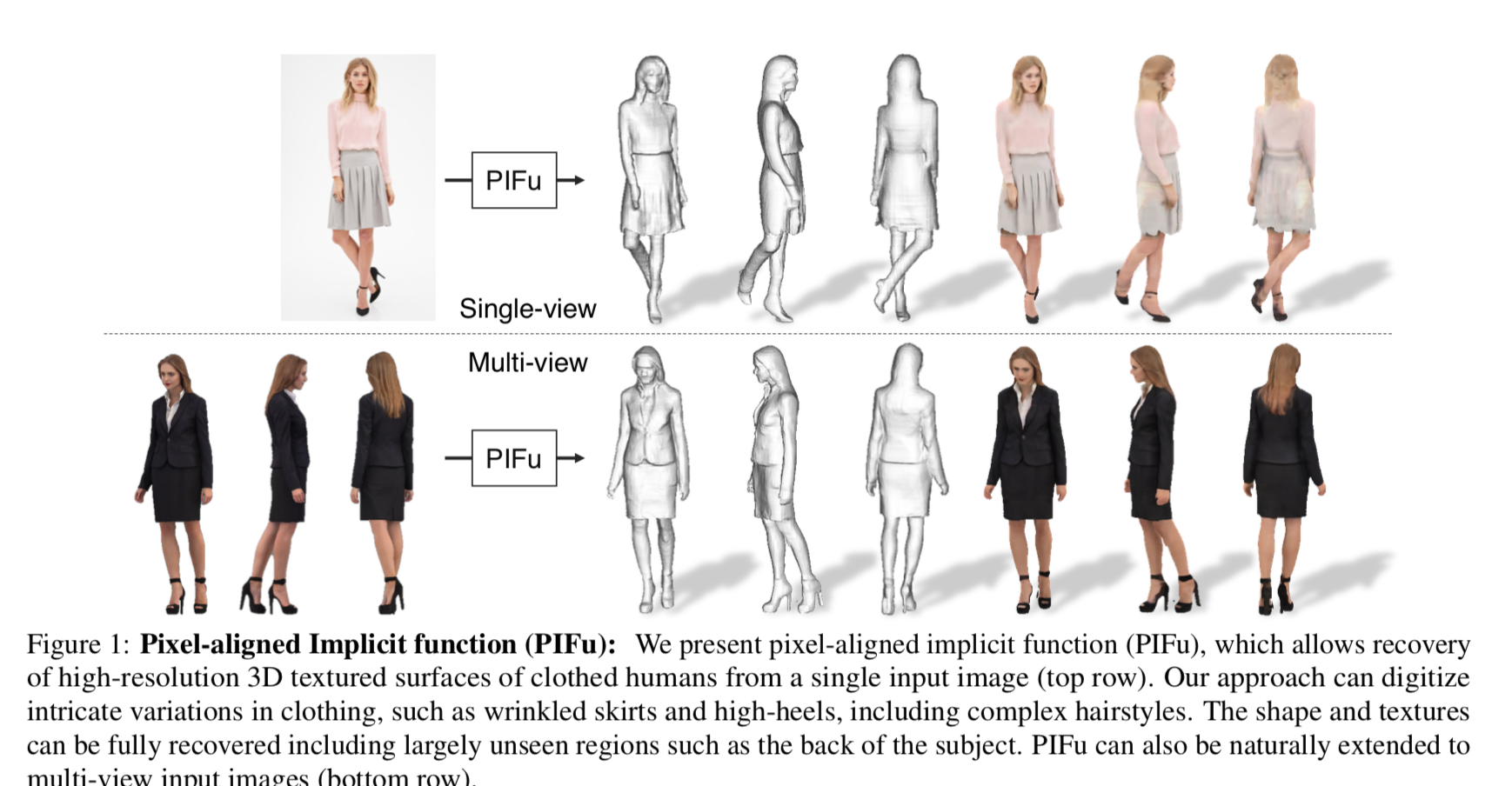
上側は1枚の画像を入力した場合で、下側がmultiな視点からの画像を入力した場合。いずれも3次元の形状、およびテクスチャを推定している。
手法
もろもろ定義
$X$ ・・・3次元のカメラ座標におけるある点の位置。
$x = \pi(X)$ ・・・ $X$ を二次元にprojectしたもの
$I(x)$ ・・・ その Image
$z(x)$ ・・・カメラ座標における depth。
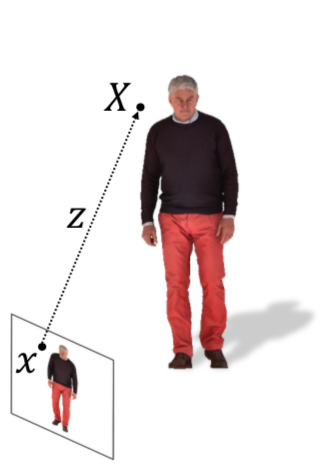
$g$ ・・・入力画像($I(x)$ ?)をエンコードする encoder。
$F(x) = g(I(x))$ ・・・入力画像をエンコードして得られる特徴量。
$F_v(x)$ ・・・surfaceに関する特徴量。
$F_c(x)$ ・・・textureに関する特徴量。

おそらく、$F$ はこのように入力画像と同じサイズにencode, decodeされ、その特徴マップ上の位置 $x(h, w)$ は画像上の $x(h, w)$ に対応していて、
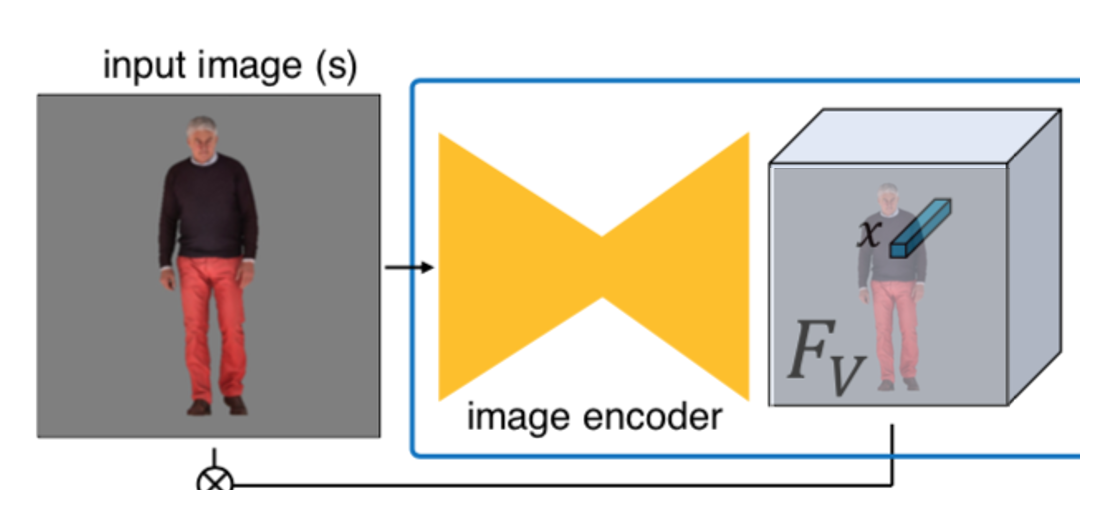
チャンネル方向の次元は特徴量の次元だろう。
陰関数の表現
特徴量 $F(x)$ と $X$ までのdepth $z(X)$ を用いて surface は以下のように表す。
f(F(x), z(X)) = s:s \in \mathbb{R}

surface の学習
まず陰関数のtargetは
f^*_v (X) = \left\{ \begin{array}{ll}
1 & if\ X\ is\ inside\ mesh\ surface \\
0 & otherwise
\end{array} \right.
として、推論値とのMSEをlossとする。
\mathcal{L}_v = \frac{1}{n} \sum^n_{i=1} |f_v (F_V (x_i), z(X_i)) - f^*_v ( X_i)|^2
推論時は陰関数の値が $0.5$ となるところを表面とする。
data のサンプリング方針

データとなる点 $X$ は空間上から一様に取得すると、ほとんどが体表面から外れたものとなり、その結果、体表面の推定が困難なモデルができるだろう。
一方で体表面周囲のみから取得すると、過適合になるだろう。
そこで本手法では以下の1、2を $16:1$ の比率で混ぜて使う。著者によると、ここを変えると学習がうまくいかないらしい。
- 体表面から正規分布 $\mathcal{N}(0, \sigma), \sigma=5.0 \ cm$ に従う値だけ外れた位置からサンプリングする
- 空間上の一様分布からサンプリングする
Texture Inference
テクスチャに関しても
\mathcal{L}_C = \frac{1}{n} \sum^n_{i=1} |f_c (F_C (x_i), z(X_i)) - C ( X_i)|^2
としたいところ。ここで $C(X)$ は $X$ におけるRGB値。
しかし著者らに言わせると、この学習は進まない。問題点はこの図のように

$F_C$ が $(x, z)$ ・・・つまり空間上の位置 $X$ に対して体表面の RGB を推定するためにはそもそも体表面自体も推定しなければならない点。
そこで texture inferenceにsurface Reconstruction で推定した $F_V$ を入れることでこれを回避する。
\mathcal{L}_C = \frac{1}{n} \sum^n_{i=1} |f_c (F_C (x'_i, F_V), X'_{i,z}) - C (X_i)|^2
ここで $X'_i = X_i + \epsilon \cdot N_i, \ N_i \sim \mathcal{N}(0,d)$ として体表面から一定の距離の位置に対しても色付けする。

改めてモデルの図を見ると、Surface Reconstruction で推定した $F_V$ が Texture Inference に入力されている。
multi-view stereo 画像の場合
multi-view のデータがある場合、この図のように

まず $f_1$ でこれまでと同様 single-viewからの陰関数を推定し、
\Phi_i = f_1(F_i(x_i), z_i(X))
次に $f_2$ でそれぞれの view からの陰関数を集計して包括的の陰関数を求める。
f_2 (\Phi_1, \cdots , \Phi_n) = s
実験と結果
1. 定量的評価
メトリクスは以下
- the average point-to-surface Euclidean distance(P2S)
- Chamfer distance
- normal reprojection error
simgle-viewで RenderPeople dataset と BUFF dataset で学習させた結果は以下。

いずれのメトリクスで見ても他の手法よりよい。
multi-viewで RenderPeople dataset と BUFF dataset で学習させた結果は以下。

こちらも他の手法より全般的に良い。
2. 定性的評価
DeepFashion dataset で学習させた場合の推論した surface と texture は以下。

いぃ感じに生成されてる。
また以下は他のモデルと出来具合を比較した画像。
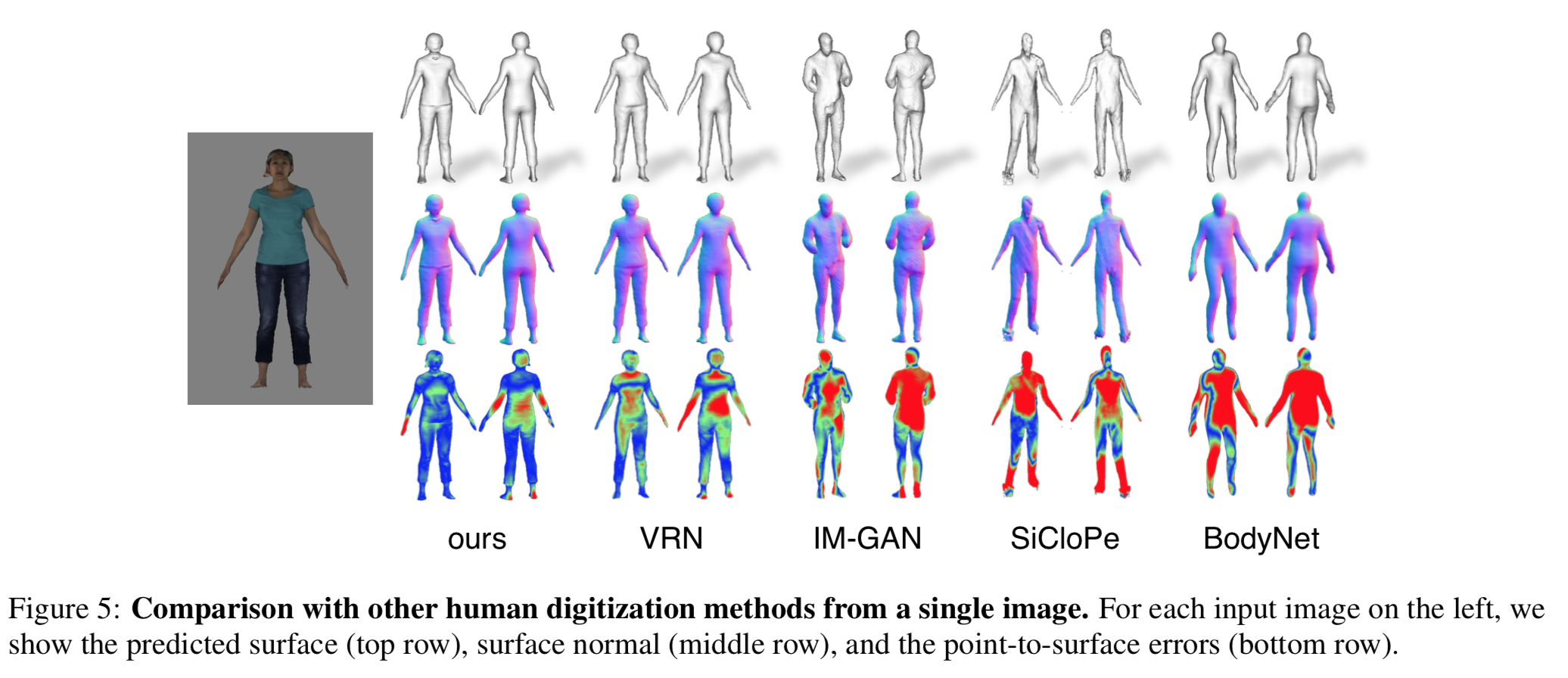
3. ablation study
multi-viewのあるデータに対してviewを増やしていった時に精度が上がるか、の検証は以下。
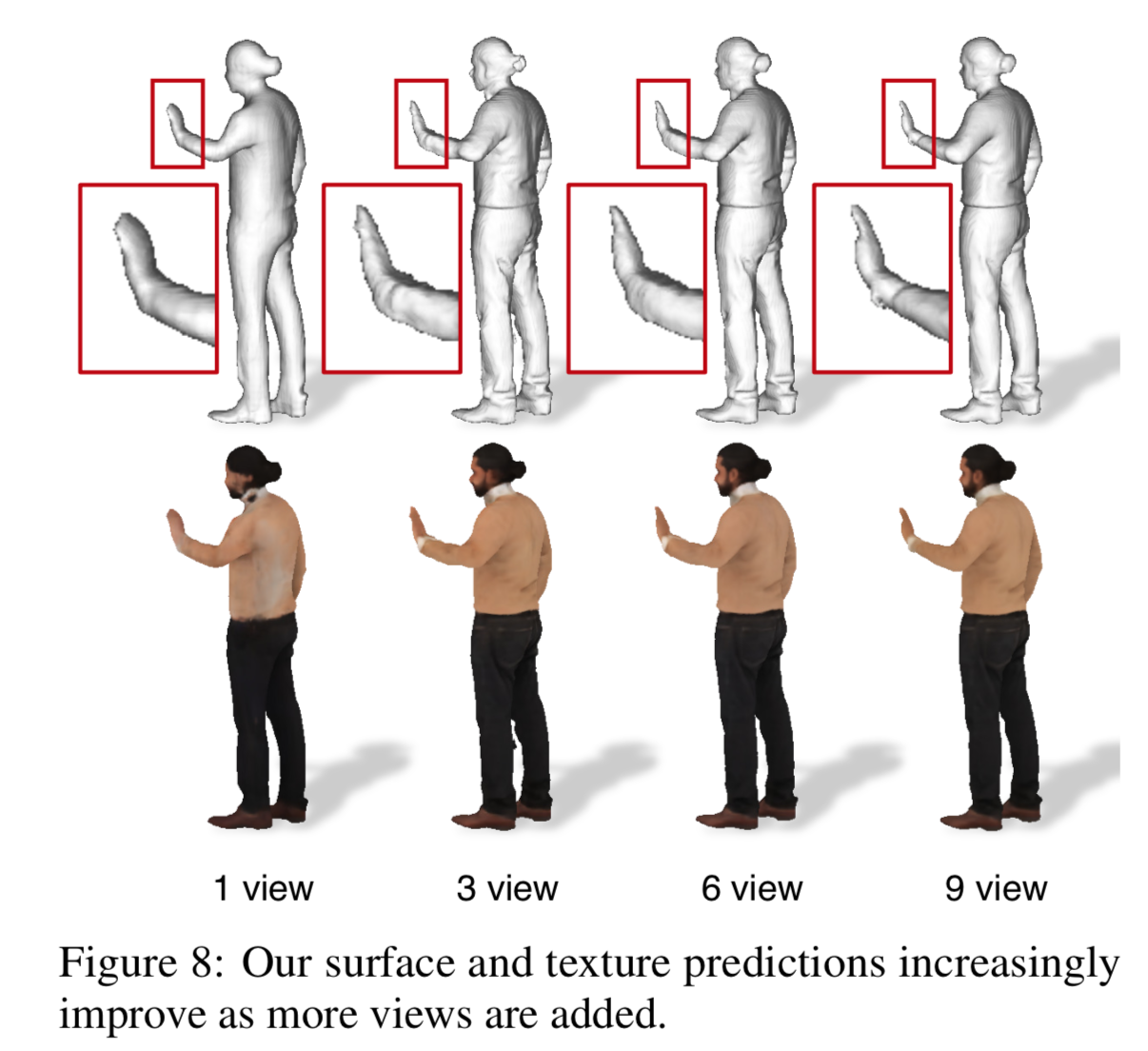
multi-viewの増加に伴って、よりdetailが取れるようになってる。