はじめに
KaggleのCarvana Image Masking Challengeで1位を取ったモデル:TernausNet の論文をまとめてみた。
[1] V. Iglovikov, et. al. "TernausNet: U-Net with VGG11 Encoder Pre-Trained on ImageNet for Image Segmentation"
arXiv:https://arxiv.org/abs/1801.05746
著者らのGithubコードは公開されている。
https://github.com/ternaus/TernausNet
概要
- U-Net に転移学習を適用させ、有効性を実証した
アーキテクチャ
[1]のFigure 1より
見た通り、通常のU-Net構造だが、encoderだけVGGNetを転移学習させる。
転移学習させるVGG-11のネットワークはこれ。
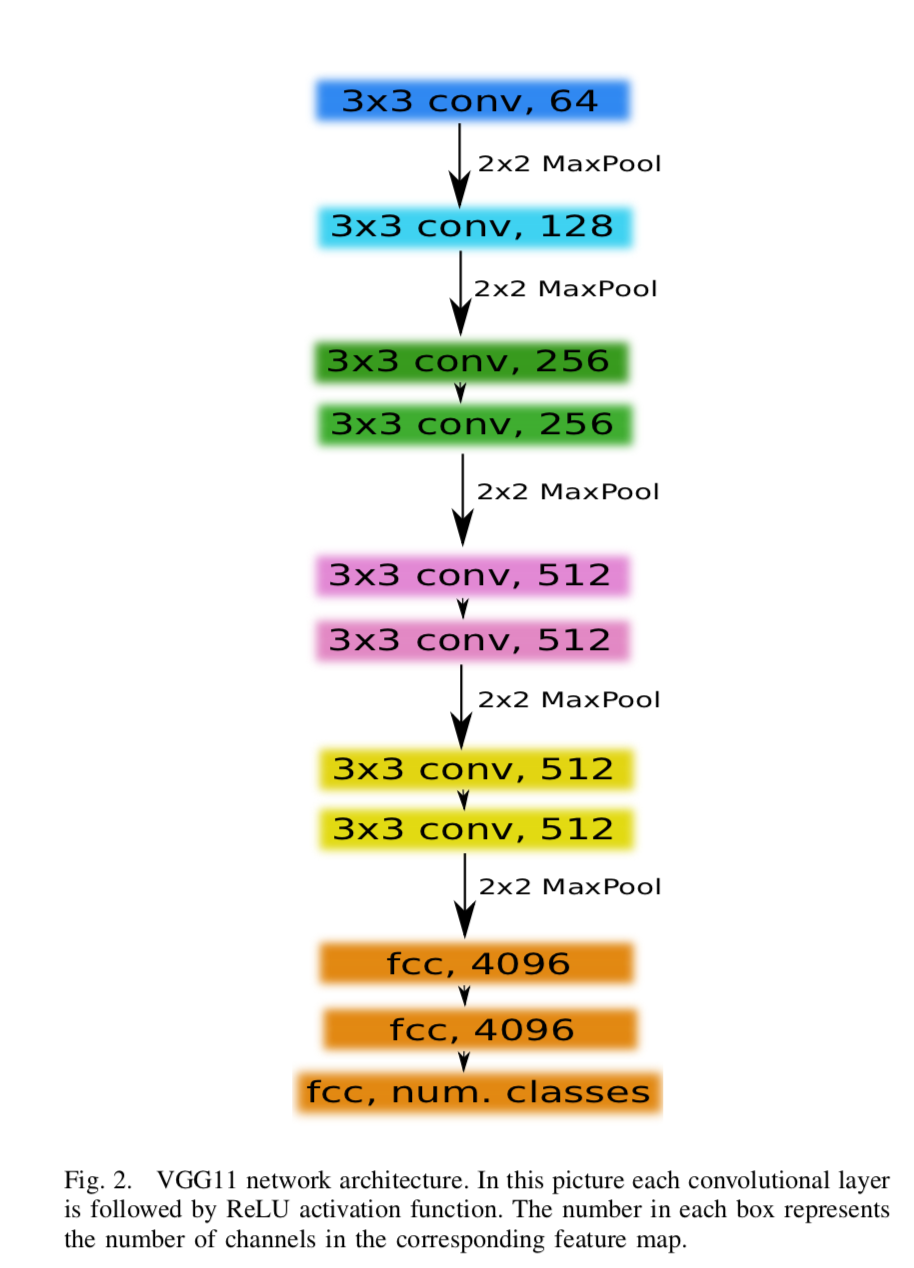
[1] Figure 2 より
よく見かけるVGG-11。このオレンジの部分(fully-connected)を取り払って、1つのconv層を追加し、encorderとする。
メトリクス
以下のIoU(Jaccard index)。
J(A,B) = \frac{| A \cap B |}{| A \cup B |} = \frac{| A \cap B |}{| A | + | B | - |A \cap B |}
目的関数
2つの要素から構成される。1つ目はメトリクスのIoUを直接求める。
J = \frac{1}{n} \sum^n_{i=1} \left( \frac{y_i \hat{y_i}}{y_i + \hat{y_i} - y_i \hat{y_i}} \right)
ここで $y_i$ はi pixelのtarget、$\hat{y_i}$ は同推論値。
もう1つは通常のcross entropy。
H = - \frac{1}{n} \sum^n_{i=1} \left( y_i \log \hat{y_i} + (1-y_i)\log (1-\hat{y_i}) \right)
トータルのlossはこれら2つを足す。具体的には H に J の negative-logを足す。
L = H -\log J
実験と結果
転移学習の有効性を証明するため、転移学習したものとしないもので比較実験を行なった。
実験の設定は以下
- データセット:Inria Aerial Image Labeling Dataset
- 最適化:Adam learning rate=0.001
- data augmentation:crop
転移学習しないモデルは以下の LeCun uniform initializerでパラメータを初期化した。
- $L = \sqrt{\frac{1}{f_{in}}}$ として $[-L, L]$ の一様分布から得る
結果
- LeCun uniform initializer:IoU=0.593
- ImageNetで学習したVGG11の転移学習:IoU=0.686
- Carvanaデータセットで事前学習したモデルの再学習:IoU=0.687
学習曲線は以下。
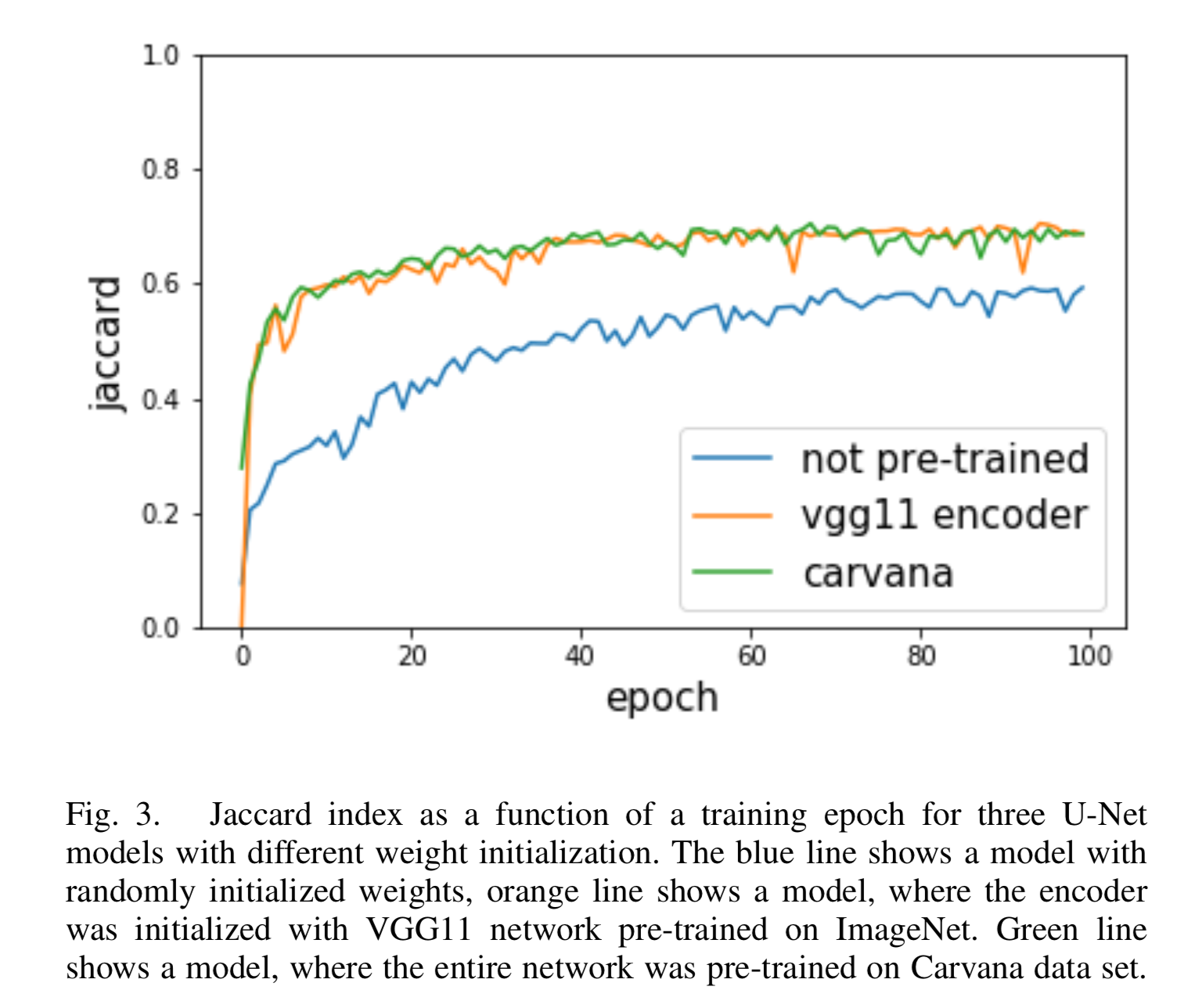
[1] Figure 3より
結論
- 転移学習はU-Netモデルでも有効
今後の展望
今回はVGG11の転移学習だったが、これをVGG16やResNetにすると、さらに精度が上がるのではないか。
個人的感想
この論文が出る前からコンペとかでsemantic segmentationモデルに転移学習を適応させていた方は多いと思うが、改めて論文にまとめてくれた点は有難い。
