はじめに
GANを使った異常検知論文からその先駆け的存在の以下
[1] T. Schlegl, et. al."Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery" IPMI 2017
をまとめる。
arXivのページ
https://arxiv.org/abs/1703.05921
githubにいくつかコードがあがってるが
https://github.com/xtarx/Unsupervised-Anomaly-Detection-with-Generative-Adversarial-Networks
それらが著者らのかどうかは不明
概要
- GANを使って異常検知をするモデル
- 正常・異常を分類するモデルではアノテーション作業が膨大 or 異常データが少ないので、正常のみから学習するという点で意義がある
- 網膜等医療系の画像で効果を実証した
モデルの全体像
以下の[1] figure 1で説明すると
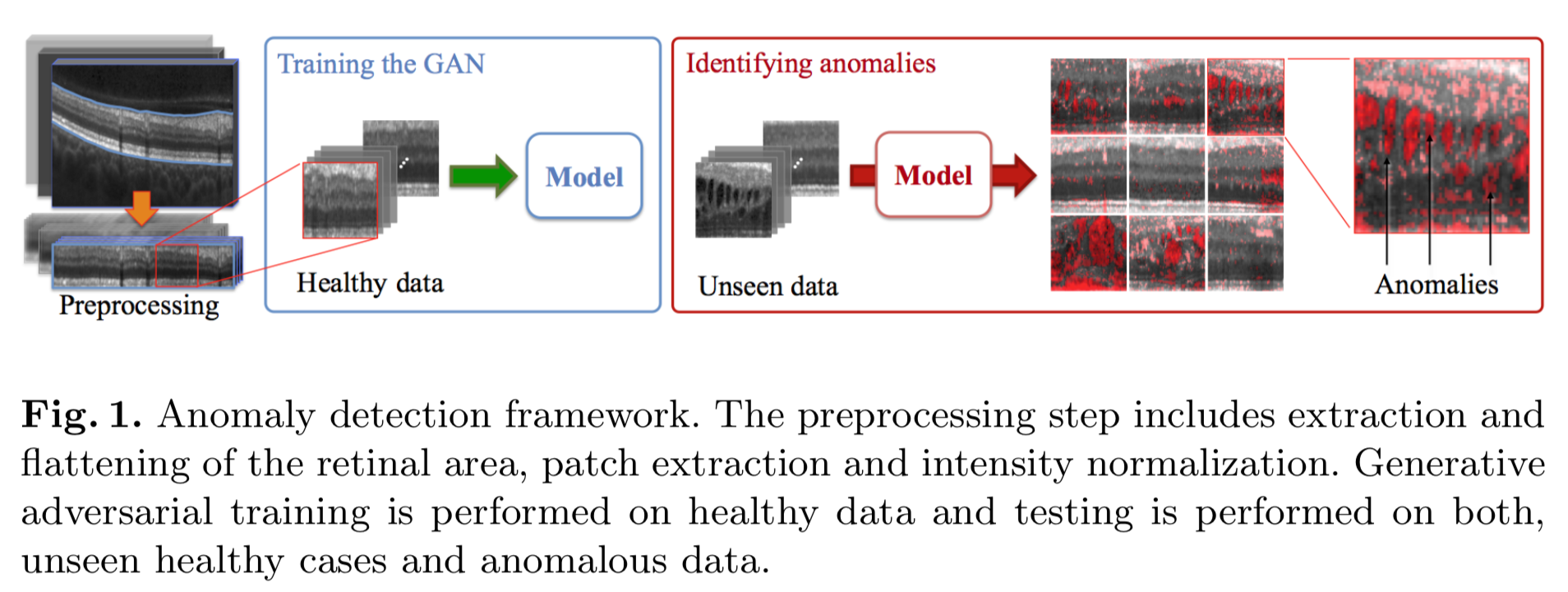
大きく分けて以下2つのフェーズがある。
1)正常データを生成するよう学習するフェーズ
2)学習したモデルで未知のデータに近いもの生成するノイズを探索するフェーズ
フェーズ1
figure 1 の左上が網膜付近の画像。これから前処理で網膜部分を切り取り、平らにした画像がその下。
これからパッチを切り取り、正規化したものを正常データとする。
正常データを生成するよう、その右(Training the GAN)のGANで学習する。
フェーズ2
右半分(Identifying anomarilies)の左から未知データを入力する。
これに対し、異常と判定されたエリアが右からの出力画像の赤い部分。
フェーズ1:正常データを生成するようGANで学習
GANのアーキテクチャ
GANのアーキテクチャは以下の[1]figure 2 の(a)。
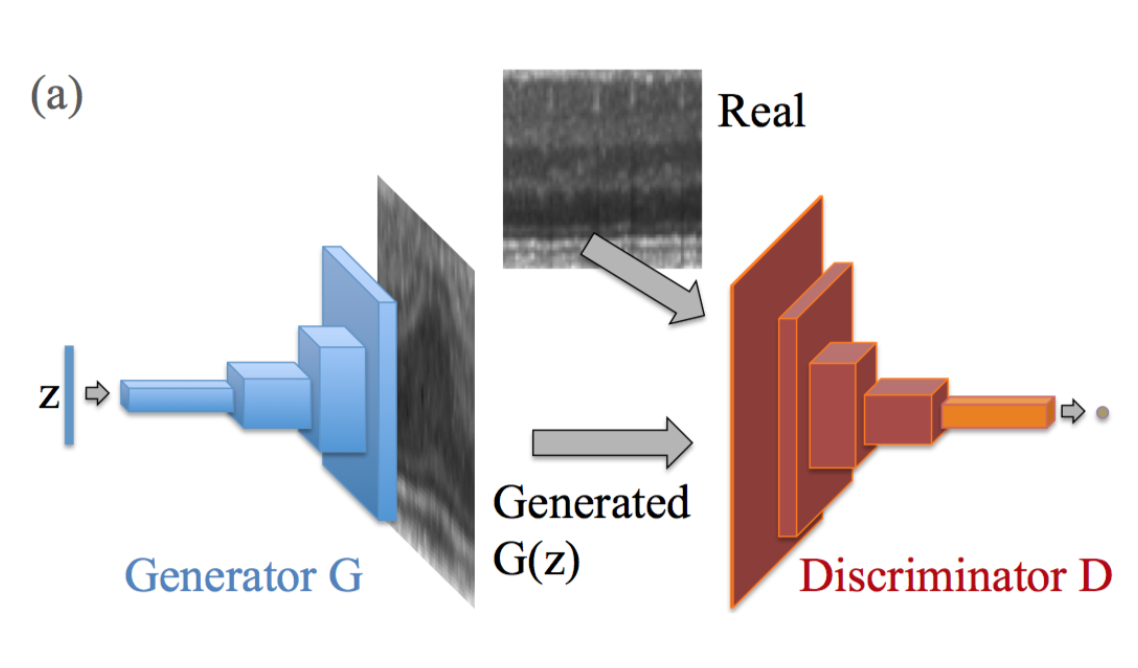
スタンダードなGAN構造。
目的関数
1次元のノイズ $\bf z$ とそれが従う一様分布 $p_{\bf z}$ 、
入力画像 $\bf x$ とそれが従うデータ分布 $p_{data}(\bf x)$ 、
generator:$G$、
discriminator:$D$ としてminimaxな式は以下のスタンダードなもの。
\min_G \max_D V(D, G) = \mathbb{E}_{\bf x \rm \sim p_{data}(\bf x \rm)} [\log D(\bf x \rm)] + \mathbb{E}_{\bf z \rm \sim p_{\bf z \rm}(\bf z \rm)} [\log (1 - D(G(\bf z \rm)))]
フェーズ2:異常検知
学習したGANを異常検知に利用するには特殊な処理が必要。
異常検知の全体像
1)適当な $\bf z\rm_1 \sim p_{\bf z}$ で生成した画像 $G(\bf z\rm_1)$ と未知の画像 $\bf x$ とのロスを求める
2)勾配降下法でより未知の画像 $\bf x$ に近い画像を生成する $\bf z\rm_2$ を求める
3)生成した画像 $G(\bf z\rm_2)$ と未知の画像 $\bf x$ とのロスを求める
4)以上の繰り返しで未知の画像 $\bf x$ に最も近い画像を生成するノイズ $\bf z\rm_{\gamma} $ を求め、これにより生成した画像 $G(\bf z\rm_{\gamma})$ と未知の画像 $\bf x$ との距離で正常・異常を判定する
フェーズ2のロス
ロスは2種類。
- 未知の画像 $\bf x$ と生成した画像 $G(\bf z \rm)$ との見た目の近さを測る residual loss
- 生成した画像 $G(\bf z \rm)$ が正常データ $\chi$ の多様体に含まれるかを測る discrimination loss
residual loss
residual loss は以下のL1。
\mathcal{L}_R (\bf z\rm_{\gamma}) = \sum |\bf x\rm - G(\bf z\rm_{\gamma}) |
discrimination loss
discrimination loss は以下のようなDiscriminatorの中間層からの出力同士のL1。
\mathcal{L}_{D} (\bf z\rm_{\gamma}) = \sum | f(\bf x\rm ) - f(G(z\rm_{\gamma}))|
トータルのロス
上記2つのロスを組み合わせて、最終的なロスは以下。
\begin{eqnarray}
\mathcal{L} (z\rm_{\gamma}) = (1-\lambda) \cdot \mathcal{L}_R (\bf z\rm_{\gamma}) + \lambda \cdot \mathcal{L}_{D} (\bf z\rm_{\gamma}) \\
\end{eqnarray}
正常・異常の判定
正常・異常の判定には、探索して求まった最終的な $(\bf z\rm_{\Gamma})$ に対して以下のスコア $A(\bf x\rm)$ を用いる。
A(\bf x\rm) = (1- \lambda) \cdot R(\bf x\rm) + \lambda \cdot D(\bf x\rm)
ここで $R(\bf x\rm)$ はresidual loss。
また $D(\bf x\rm)$ は discriminatorからの出力に対する sigmoid cross entropy。
\mathcal{L}_{\hat{D}} (\bf z\rm_{\gamma}) = \sigma (D(G(\bf z\rm_{\gamma})),1.)
実験と結果
書きかけ