IndianBuffetProcessと潜在特徴モデル
IBP(Indian buffet process)を使って潜在特徴モデルの実装を行います。
モチベーション
IBPを使って潜在特徴モデルの実装を行うことが目的です。まずここでいう潜在特徴モデル(線形因子モデル?)の説明をするためによくあるレコメンデーションの例を使います。
まず人を縦、映画の種類を横とする行列(X)があるとします。(成分は(i,j)はiによるjの評価だとする)このとき下のようにX=UVとうまく分解することによって潜在特徴を知ることができます。

例えば潜在特徴としてはアドベンチャー成分、ミステリー成分、ロマンス成分とかが考えられます。(あくまでイメージです)この時、Uは人のそれらの成分に対する好感度、Vはそれぞれの映画がどのような成分を持っているかを表します。(実際のレコメンドシステムでは欠損値の予測に使います)
他にも自然言語処理のシチュエーションだったらドキュメントの種類と単語からなる行列に対して同じようなことを考えたりするし、音声処理では音源分離の文脈で同じモデルを使います。
しかし潜在特徴の個数はいくつがいいのでしょうか?
決定論的なモデルだったら潜在特徴の個数は上手く定まるのですが、ベイズ的なモデルを組むと潜在特徴がいくつあるかを決めるのは難しくなります。
そこで潜在特徴の個数を自動的に決めるため無限次元の確率過程(IBP)を使おうというのがモチベーションです。一見分かりやすいことはできないのですが実際にZを予測した結果が下の図です。左が真のZ,右がgibbs samplingで予測したZを表しています。

どこか違うのではと一見なりますがもともと特徴量の位置(列)は交換可能なモデルなので見事に33step後には予測できていることが分かります。
今回の記事ではもう少し定式化した説明をした後、実装パートに移ります。その後、理論編としてIBPと深い関係のあるbeta processについて触れます。最後に応用例について書きます。
実装編
佐藤先生のノンパラ本[1]をそのまま実装すればできます。分かりやすいのでぜひそちらを読むことをお勧めします。ここにコードはあげてあります。
https://github.com/Ma-sa-ue/practice/tree/master/machine%20learning(python)/nonparabayes
Indian buffet process
名前の通りインド料理店での様子を表すものです。サンプリングしてみると下のようになります。
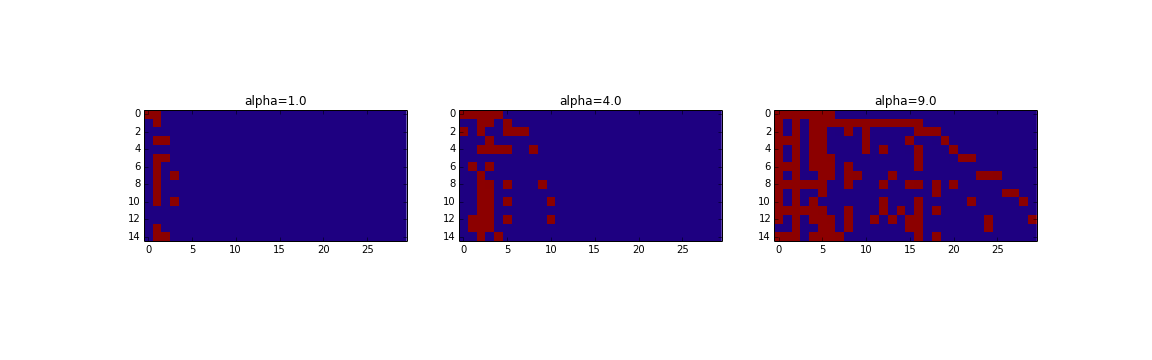
また次のように0と1からなる行列を生成することによって上のようになります。
- for i in 1,...,N(Nは行の数)
- これまで生成された列に関しては$z_{i,k}\sim Bernoulli(\frac{m_{i-1,k}}{i}$) の確率で1を生成($m_{i,k}$は行1からiまでに1が生成された個数)
- 新たな列として$m\sim Poisson(\frac{\alpha}{i})$個1を生成
感覚的には簡単で人が順番に好きな料理を取っていくという様子を表しています。具体的には人が縦、料理が横です。順番に人が来て今までのある料理に関しては人気なものほど多くとり、またそれだけだと飽きるので新たな料理を頼むということを繰り返していきます。
$\alpha$は拡散具合を表すハイパーパラメータで大きいほど色んな料理が出てくることが分かります。
このままだと交換可能性に問題があるように見えますが、実はIBPはbeta-bernoulli生成モデルのバイナリ行列の履歴の分布であるということが重要です。
今回考える潜在特徴モデル
$x_{k}$をD次元ベクトルとしたときに
$x_{k}\sim N(0,\sigma_{X}^{2}I)$,$y_{k}\sim N(\sum_{k=0}^{\infty}z_{i,k}x_{k},\sigma_{y}^{2}I)$
でZのpriorとしてindian buffet processが入っているとします。
行列表記にすると$Y=ZX+E$となります。
実装
まず状況として以下のような状況を考えます。
上の状況において一番が左がY,真ん中がZ,右がXです。
観測されるのはYだけということに注意してください。

方針としては順番に条件付き分布に沿ってZとXをgibbs samplingしていく感じです。
gibbs samplingを繰り返していくと以下のようになります。

特徴量は交換可能なのでうまく予測できていることが分かります。
実際はこのようにぴったりになることはあんまりないです。
理論編
beta processからのサンプリングとIBPとbeta processの関係について書きます。
詳しくは[4],[6]に載っています。
Levy process
Levy processは定常な独立な増分を持つ確率過程です。かなり一般的な確率過程で様々な確率過程を含んでいます。まずLevy-ito decompositionによりlevy processはdrift付きのBrownian motionとjump processに分けることができます。
Jump processが今回の本題です。Jump processはjumpしているような確率過程でpoisson process,beta process,gamma processを含みます。
まず大前提としてこのように単調にjumpしていくlevy processはrandom measureに対応します。そしてlevy processはlevy measureによって特徴づけることができます。
levy measureとrandom measure(levy process)の対応がサンプリングしたいときは重要でlevy measureをmean measureとするようなpoisson processによりrandom measure(levy process)を構成することができます。
Poisson process
Poisson processからのシミュレーションについて考えます。基本的には二通りのシミュレーションの仕方があります。
一つ目は順番に人がくるとして次々に人をサンプリングしていく手法。
二つ目は順番にあらかじめ何人来るか定めて強度関数(mean measure)に応じてその人たちを配置する手法です。
Beta processからのサンプリングにおいては後者を使います。詳しくは[7],[8]をみてください。
Beta process
$\Omega$上のbeta processを考えます。
Beta processでは$B(d\omega)\sim Beta(c\mu (d\omega),c(1-\mu (d\omega)))$となっています。
このときBeta processに対応するLevy measureは$B_{0}$を基底測度とするとき
$\nu(d\omega,dp) = cp^{-1}(1-p)^{c-1}dp B_{0}(d\omega)$
です。つまりBeta process:Bは上のlevy measureをmean measureとするpoisson process$(\omega_{i},p_{i})(i=1,2,..)$から$B = \sum_{i}p_{i}\delta_{\omega_{i}}$と構成されます。
残念ながら$p^{-1}(1-p)^{c-1}$の(0,1)の積分は有限とならないので上手い方法を考えます。
そこで$\pi^{-1}=\sum_{k=0}^{\infty}(1-\pi)^{k}$を利用して$\nu$はさらに分解することができると分かります。すると
$\nu = \sum_{k=0}\nu_{k}$
$\nu_{k}(d\pi, d\omega)=Beta(1,c(\omega )+k)d\pi \mu_{k}(d\omega )$
$\mu_{k} = \frac{c(\omega)}{c(\omega)+k)}\mu(d\omega)$
となります。これを使ってサンプリングを行います。
Beta processからのサンプリング
上に従うとアルゴリズムは以下のようになります。
- sample the number of points many times : $n_{k}\sim Poisson(\int_{\Omega}\mu_{k}(d\omega))$
- for each k, sample $n_{k}$ points from $\mu_{ki}$:$\omega_{ki}\sim\frac{\mu_{k}}{\int_{\Omega}\mu_{k}(d\omega)}$
- sample $p_{ki}\sim beta(1,c(\omega_{ki})+k)$
- then $\cup_{k=0}^{\infty }{(\omega_{ki},p_{ki})}$ is a realization
例えば$\mu_{k}$を一様,$\Omega=[0,1]$,$\int_{\Omega}\mu_{k}(d\omega)$を$\gamma$とすると
次のようなグラフが書けます。
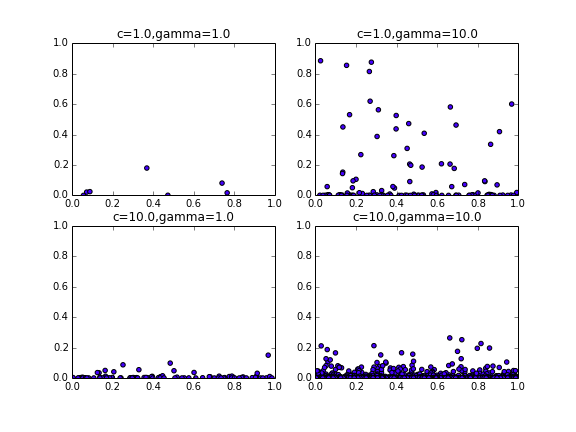
また実際に$\gamma=10.0$のとき何回かサンプリングを行ってみると$B(\Omega)$の平均はだいたい10になります。
Beta processとIBPの関係
[4]に詳しくは書いてあります。こちらの論文ではbeta processのサンプリング手法もibpとの関連から導出しています。
De Finetti's Theoremによるととexchangebleな観測列$Z_{1},...,Z_{n}$は
$P(Z_{1},...,Z_{n} )= \int[\prod_{i=1}^nP(Z_{i}|B)]dP(B)$
となりました。
IBPではP(B)がbeta processに対応していて$P(Z_{i}|B)$がpoisson processに対応していることになります。
二つのパラメータによる一般化
IBPはパラメータが一つ分布モデルにおけるbeta bernoulli分布のパラメータを二つにすることによってさらに一般化することができます。またこれはbeta processにおけるcと$\gamma $を変えることにも対応しています。
応用例
IBPの応用例というより行列分解による潜在特徴モデルの応用例なのですが雑多に挙げてあります。Griffithsによるreview[3]を軽くまとめた感じです。
全般的なこと
probabilistic PCA,factor analysis,sparse codingなどの線形因子モデルについては下にまとめてあります。
http://qiita.com/masasora/items/431afb71eae60a1c826b
推薦システム
もう既によい文献もまとめたページ([10],[11],[12])は沢山ありますが、一応説明します。
推薦システムには一般的に3つのやり方があります。
1つ目は基本的な統計量をそのまま使うやり方です。例えば売れている店や売れている商品をそのまま推薦するとかです。
2つ目は協調フィルタリングです。user basedとitem basedがあります。例えばuser basedだったらある人(A)のある商品(B)の評価を予測するためにAに似ている人のBの評価を取ってきてAによるBの評価を予測するという感じです。
3つ目が行列分解による方法です。最もbasicな方法がSVDによる行列分解でX=SVDとなった時、XをSとVDに分解することで今まで述べてきたよう行列を分解します。しかし実際は欠損値とかあったり負の評価はおかしかったりするので、これをさらに発展(もはやSVDではない?)方法が多々あります。用途によりますが、単純な予測性能だけを言うと基本的には3に基づく手法が優れています。また分解した行列を利用して似たユーザーや似た映画を知ることもできます。
本題に戻るとIBPが使えるのは3の手法です。
音声処理
音声処理の典型的な応用例としてが音源分離の問題があります。注意することとしてはXのpriorがgaussianではないということがあります。例えばlaplace分布であったりt分布します。
生物学
一つ目の応用として遺伝子と細胞の発現レベルを表す行列(Z)の分解があります。遺伝子iが細胞kで発現しているか否かが$z_{ik}$になっています。
また他にはタンパク質の相互作用を調べるという応用があります。タンパク質$i$がcomplex$k$に属しているか否かが$z_{ik}$になっているということです。分解した行列を利用して似たタンパク質を知ることができます。(つまり$\sum z_{ik}z_{jk}$が大きいほど似ている。)
参考文献
- 佐藤先生のノンパラ本 アルゴリズムや理論的なことがとても簡潔にまとまっている。
http://www.kspub.co.jp/book/detail/1529151.html - 佐藤先生のスライド http://www.slideshare.net/issei_sato/ss-37837949
- IBPを勉強すると絶対お目にかかるreview https://cocosci.berkeley.edu/tom/papers/indianbuffet.pdf
- Beta processとIBPの関連について書いてある 階層beta processの作り方も http://www.cs.berkeley.edu/~jordan/papers/thibaux-jordan-aistats07.pdf
- Beta processとか含めて機械学習のためのnonparaということでいろいろ書いてある。上と同じ著者。(jordanの弟子)
http://digitalassets.lib.berkeley.edu/techreports/ucb/text/EECS-2008-130.pdf - Beta processとかgamma processからのサンプリング手法についてのっている。
http://people.ee.duke.edu/~lcarin/Yingjian_ICML_2012.pdf - poisson procesについて意外とわかりやすくまとまっている。(Wikipedia)
https://en.wikipedia.org/wiki/Poisson_point_process#Simulation - poisson processについて 理研での講義資料?
http://toyoizumilab.brain.riken.jp/hideaki/res/lecture/point_process.html - Linear factor modelについてまとまってる章がある。(BengioたちのDeep learningの本です)
http://www.deeplearningbook.org/contents/linear_factors.html - 推薦モデルについてわかりやすくまとまっている。 http://ameblo.jp/principia-ca/entry-10980281840.html
- 推薦モデルについてわかりやすくまとまっている。http://smrmkt.hatenablog.jp/entry/2014/08/23/211555
- Courseraの授業の教科書 推薦モデルについて纏まっているパートがあるhttp://infolab.stanford.edu/~ullman/mmds/book.pdf
- 測度論的確率論は和書だと舟木さんの洋書だとwilliamsのが定番(連続時間の確率過程の本は厳密に勉強したことがないのですがBrownian motionだとshereveの本が一般的だと思います。"for finance"となっている方は厳密ではないですが読みやすいです。点過程の本は何がいいのでしょうかね...)
- Handbook of markov chain monte calro 点過程ついても計算統計の観点から丁寧に書かれている http://www.mcmchandbook.net/HandbookTableofContents.html