More than 5 years have passed since last update.

CNTK 2.2 Python API 解説 (2) - マルチノード分散トレーニングの実装と実行 / ベンチマーク

Last updated at 2017-11-05Posted at 2017-11-05

CNTK 2.2 Python API 解説 (2) - マルチノード分散トレーニングの実装と実行 / ベンチマーク

0. はじめに

◆ CNTK ( Microsoft Cognitive Toolkit ) 2.2 の Python API 解説第２弾です。
今回は CNTK の分散トレーニング、特にマルチノード構成における分散トレーニングの実装・実行方法の解説とベンチマークの結果報告になります。
ユーザ設定が必要な初期値 (ウォームスタートサイズ, ブロックサイズ) についても適正値を検証しています。
また、CIFAR-10 用にカスタマイズした BN Inception, ResNet-110 モデルを分散トレーニングすることによってテスト精度 94.04 % を達成しています。

これまでは主として CNTK 2.2 Tutorials への橋渡しを意識した記事作成を心がけてきましたが、
今回はリファレンスマニュアルを参考に、サンプルプログラムを利用した分散処理の実験報告です。

◆ CNTK 2.2 を新たに学び始めた一番の理由は、分散トレーニングへの期待です。
他の幾つかの深層学習フレームワークで分散トレーニングに挑戦してみましたが、
個人的に試した限りでは以下のような短所の何れかを持つケースが目立ち、良い感触が得られていません :

分散対応に必要なコード変更量が多すぎて、手軽に利用できない。
柔軟性に欠けていて、雛形に落とし込むことがタスクによっては困難。
パフォーマンス (速度・精度) が出ない。速度が出なかったり、速度が出ても精度が極端に落ちる。
具体的な分散アルゴリズムが不明。
(開発途上なのかもしれませんが) 安定感に欠けて現時点で利用しづらい。

そこで CNTK です。
CNTK では並列データ処理、とくに "1-bit SGD" アルゴリズムの実装をセールスポイントにしていますので分散処理を重視しているはずです。そして分散処理フレームワークとして MPI 仕様ベースの OpenMPI 実装を利用していますから全体像の理解が容易ですし、かつステーブルであることも期待できます。

◆ 今回実験した結論として、CNTK の分散トレーニングについて以下のような 優位点 が確認できました :

実装が非常に簡単です。分散トレーニングへの対応に必要なプログラムの改変は最小限で済みます。
少なくとも 4 ノードあれば明確にパフォーマンス改善が得られます。大幅な速度の改善が見られ、精度の劣化もアルゴリズムの選択により最小限に抑えることができます。
ジョブの投入も MPI をベースにしているのでスムースで手軽です。
複数のデータ並列アルゴリズムから選択できますので、モデルやデータセットについて最適化できます。
それぞれのアルゴリズムの主目的 (勾配交換の効率化や非並列化トレーニングの活用等々) が明確ですので、高速化のポイントが抑えやすいです。

【マルチノード構成に関する補足】
なお、マルチノード (・シングルワーカー) 環境 - つまり 1 GPU 装備の (仮想) マシン複数台で構成された環境を選択した第一の理由は、4 GPUs や 8 GPUs を装備した (仮想) マシンを調達するよりも一般にはハードルが低いと考えためです。

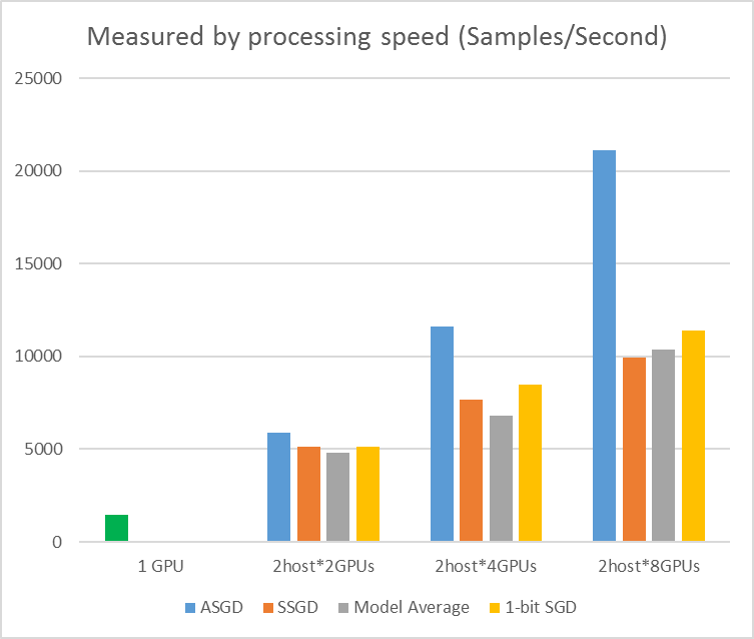
また同じ GPU デバイス総数で比較した場合、(試した限りでは) ワンノード・マルチワーカーはマルチノード構成ほどのパフォーマンスは得られませんでした。これは I/O がボトルネックになっている可能性が考えられます。もちろんモデルやデータセットによっては異なる結果になるでしょう。アルゴリズムの選択も影響を与えるはずで、下図のグラフを見ると "ASGD" の選択はマルチワーカーについて顕著な改善を示しています。

もちろん、理想的には複数 GPU を装備した (仮想) マシンを複数用意してマルチノード・マルチワーカーを追求するのが良いでしょう。

本記事の内容 :

動作環境について
CNTK 分散トレーニングの基礎知識
分散トレーニング例題
ベンチマーク
CIFAR-10 分散トレーニングの結果

本記事は以下のドキュメントと Python サンプルプログラムを参考にしています :

1. 動作環境について

動作環境

動作環境の構築が必要な場合には、Cognitive Toolkit 2.2 を Azure Linux GPU 仮想マシンにインストールを参考にしてください。Azure ポータルと Ubuntu Linux にある程度慣れていれば、30 分程度で以下のような環境が構築できるかと思います :

Azure NC 仮想マシン with NVIDIA Tesla® K80 GPU
Ubuntu 16.04 LTS
NVIDIA CUDA 8.0 & cuDNN 6.0
Anaconda 3 4.1.1
CNTK 2.2 (for GPU)

※ 本記事ではマルチノード環境、つまり GPU 装備の仮想マシン複数台で構成された環境を利用しています。
そのためには、ご利用のサブスクリプションによってはクォータ制限の拡張が必要となるケースがあるかもしれません。ご留意ください。

2. CNTK 分散トレーニングの基礎知識

CNTK の分散トレーニングの基礎知識は次のドキュメントで得られますが、この章で Python 実装に必要な要点を簡単にまとめておきます :

Multiple GPUs and Machines

Python API を使用するプログラミング視点では特に難しい話しはありませんが、
ウォームスタートサイズやブロックサイズ等のユーザ設定が必要な初期値の適正値がドキュメントでは明示されていません。
もちろんモデルやデータセットにも依存するためでしょう。これについても後で実際に検証してみます。

2-1 概要

CNTK は以下の４つの並列 SGD アルゴリズムをサポートしています :

但し上述のドキュメントを見る限りでは、ModelAveragingSGD と DataParallelASGD の２つのアルゴリズムについて、現時点では Python 実装あるいはドキュメントが公開されていないように見受けられます。そのため、本記事では 1. DataParallelSGD と 2. BlockMomentumSGD だけを扱うことにします。
(Python 実装がドキュメントとして公開され次第、記事を再作成する予定です。)

なお、DataParallelSGD については通常のアルゴリズムと "1-bit SGD" アルゴリズムが用意されています。

ライセンス形態

※ この項目については、意図的に直訳を心がけましたので少し文章が固いかもしれません :

SGD アルゴリズム実装の位置づけとライセンス交付については以下を参照してください。簡単に目を通しておくと良いでしょう :

２番目のライセンスは 1-bit Stochastic Gradient Descent (1bit-SGD) と Block-Momentum コンポーネントに対して特有のもので、メインの CNTK ライセンスよりもより制限的です。

Data-Parallel SGD は 1bit-SGD と共に、あるいはそれなしで使用されるかもしれません。Data-Parallel SGD が 1bit-SGD なしで使用されるときには、それはメインの CNTK ライセンスのもとにライセンスされます。1bit-SGD と共に使用されるときは、CNTK 1bit-SGD のもとにライセンスされます。

Block-Momentum SGD は、使用シナリオにかかわらず、常に CNTK 1bit-SGD ライセンスのもとにライセンスされます。注意してください、このアルゴリズムに対するソースコード実装を得るためには、1bit-SGD 自身を使用する計画がない場合でさえも 1bit-SGD を有効にするためには指示に従う必要があります。

Model-Averaging SGD の実装はメインの CNTK コードと共にストアされてメインの CNTK ライセンスのもとでライセンスされます。

2-2. Python プログラムで CNTK の分散トレーニングを構成する

さて、CNTK で分散トレーニングを行なうために実際に Python プログラムの改変を行ないます。
基本的には通常の (ローカル) learner をベースに分散 learner を作成するだけですから、非常に簡単です。
そしてその分散 learner を使用して、通常のように trainer オブジェクトを作成すれば良いです。

◆ データ並列 SGD (= DataParallelSGD) アルゴリズムを使用するためには、ユーザは分散 learner を作成して trainer に渡す必要があります。分散 learner を作成するためには、data_parallel_distributed_learner() を使用し、これは次の引数を取ります :

learner – ローカル learner (i.e. sgd)
distributed_after (int) – ウォームスタート のためのサンプル数を指定します、この (サンプル数の) 後で分散トレーニングが開始されます。デフォルトは 0。
num_quantization_bits (int) – 量子化のためのビット数 (1 to 32)。デフォルトは 32、これは量子化を行いません。

ウォームスタート は分散処理を開始する前に並列化しないでトレーニングすることを意味し、これが (分散処理による) 精度の劣化を最小限に抑えてくれます。但し、サイズを大きくし過ぎると当然のことながら速度の低下を招きます。

from cntk import distributed
...

learner = cntk.learner.momentum_sgd(...)    # ローカル learner を作成します。
distributed_after = epoch_size              # サンプル数、これでウォームスタートします。
distributed_learner = distributed.data_parallel_distributed_learner(
    learner = learner,
    num_quantization_bits = 32,              # 量子化されない勾配蓄積
    distributed_after = 0)                   # 0 はウォームスタートしません。
...
minibatch_source = MinibatchSource(...) 
...
trainer = Trainer(z, ce, pe, distributed_learner)
...
session = training_session(trainer=trainer, mb_source=minibatch_source, ...)
session.train()
...
distributed.Communicator.finalize()       # 分散トレーニングが成功した場合には MPI を finalize するために呼び出されなければなりません。

(training_session の代わりに) ユーザ定義訓練ループのためには、MinibatchSource.next_minibatch() メソッドに num_data_partitions と partition_index 引数を渡す必要があります。これによって (distributed_after サンプルが読まれた後に) 異なる MPI ノードが異なるデータ・パーティションからデータを読むことができます。

分散トレーニングが成功的に終了した場合に限り、Communicator.finalize() が呼び出されるべきであることに注意してください。分散ワーカーが失敗した場合には、このメソッドは呼ばれるべきではありません。

2-3 MPI で CNTK の並列トレーニングを実行する

CNTK の並列化は MPI (実装は Open MPI) で実装されていますので、使い方は簡単です。
CNTK v2 Python スクリプト training.py が与えられたとすると、並列 MPI ジョブを開始するためには次のコマンドを使用します :

同じ (Linux) マシン上の並列トレーニング :

mpiexec --npernode $num_workers python training.py

複数の (Linux) 計算ノードに渡る並列トレーニング :
- Step 1: ホストファイル $hostfile を作成します。name_of_node1, 2... は IP アドレスでかまいません :
```
# Comments are allowed after pound sign
name_of_node1 slots=4 # we want 4 workers on node1
name_of_node2 slots=2 # we want 2 workers on node2
```
- Step 2: ワークロードを実行します :
```
mpiexec -hostfile $hostfile python training.py
```

2-4 "1-bit SGD" によるデータ並列トレーニング

CNTK は 1-bit SGD テクニック [1] を実装しています。このドキュメントは www.microsoft.com/en-us/research/ で読むことができます :

[1] F. Seide, Hao Fu, Jasha Droppo, Gang Li, and Dong Yu,
"1-bit stochastic gradient descent and its application to data-parallel distributed training of speech DNNs,"
in Proceedings of Interspeech, 2014.

このテクニックは K ワーカーに渡り各ミニバッチを分散することを可能にします。結果としての部分的な勾配は各ミニバッチ後に交換されて集計されます。"1 bit" はデータの総量を減じるために Microsoft で開発された技術を指し、データは各勾配値について単一のビットで交換されます。

2-4-1 "1-bit SGD" アルゴリズム

各ミニバッチ後に部分的な勾配を直接交換することは法外な通信帯域を必要とします。
これに対処するために、1-bit SGD は各勾配値を... 値毎に単一のビット (!) に aggressively に量子化します。
これは実際には、大きな勾配値はクリップされ、その一方で小さな値は人工的に膨らまされることを意味します。
驚くべきことに、トリックが使用された場合そしてそのときに限り、これは収束を害しません。

そのトリックは、各ミニバッチについて、アルゴリズムは量子化された勾配 (これはワーカーの間で交換されます) を元の勾配値 (これは交換されることになっています) と比較することです。２つの差異 (量子化誤差, quantization error) が計算されて残差として記憶されます。そしてこの残差が次のミニバッチに加算されます。

結果として、aggressive 量子化にもかかわらず、各勾配値は最終的に完全な (= full) 精度で交換されます; つまり単なる遅延です。実験によれば、このモデルがウォームスタート (訓練データの小さなサブセット上で並列化せずに訓練される seed モデル) と結合される限りは、このテクニックは線形からそれほど遠くはない高速化を可能にする一方で、精度の損失がないか非常に小さい損失に導かれることを示します (制限的要因としては非常に小さなサブ・バッチ上で計算する時に GPU が非効率になることです)。

簡単に言えば、ウォームスタートと共に利用する限りは、高速化を可能にしながら精度の劣化は非常に小さい、ということです。また、上述の説明も踏まえれば、ワーカー間で交換される勾配値が 1-bit に量子化されているためにマルチノードによるオーバーヘッドも小さいはずと推測できます。

最大効率化のためには、このテクニックは自動的なミニバッチ・スケーリングと結合されるべきです、そこでは trainer は時にミニバッチ・サイズを増やそうとします。次のエポックの (データの) 小さいサブセット上で評価する際、trainer は収束を害しない範囲で最大のミニバッチサイズを選択します。これは、CNTK がミニバッチ・サイズが不可知な中で学習率と momentum ハイパー・パラメータを指定するのに役立ちます。

2-4-2 Python で "1-bit SGD" を使用する

オプションの "1-bit SGD" でデータ並列 SGD を使用する場合にも、ユーザは同様に分散 learner を作成して trainer に渡す必要があります。相違点は data_parallel_distributed_learner() の引数 :

num_quantization_bits (int) – 量子化のためのビット数 (1 to 32)。デフォルトは 32。

について、1 をセットすることです :

from cntk import distributed
...

learner = cntk.learner.momentum_sgd(...)    # ローカル learner を作成します。
distributed_after = epoch_size              # サンプル数、これでウォームスタートします。
distributed_learner = distributed.data_parallel_distributed_learner(
    learner = learner,
    num_quantization_bits = 1,              # change to 32 for non-quantized gradient accumulation
    distributed_after = distributed_after)  # warm start: no parallelization is used for the first 'distributed_after' samples
...
minibatch_source = MinibatchSource(...) 
...
trainer = Trainer(z, ce, pe, distributed_learner)
...
session = training_session(trainer=trainer, mb_source=minibatch_source, ...)
session.train()
...
distributed.Communicator.finalize()       # 分散トレーニングが成功した場合には MPI を finalize するために呼び出されなければなりません。

distributed_learner を作成する間に num_quantization_bits を 32 に変更すれば非量子化 Data-Parallel SGD を使用することになります。この場合にはウォームスタートは必要ありません。

2-5 Block-Momentum SGD

Block-Momentum SGD は以下の実装です。このドキュメントは www.microsoft.com/en-us/research/ で読むことができます :

[2] K. Chen and Q. Huo, "Scalable training of deep learning machines by incremental block training with intra-block parallel optimization and blockwise model-update filtering," in Proceedings of ICASSP, 2016.

2-5-1 Block-Momentum SGD アルゴリズム

次の図は Block-Momentum アルゴリズムの手続きを要約しています。
手続き全体としては標準的なものですが、ブロック勾配を導入している点が目新しいです :

2-5-2 Python で Block-Momentum を使用する

Python で Block-Momentum を有効にするためには、1-bit SGD の場合と同様に、
block momentum 分散 learner ( block_momentum_distributed_learner ) を作成して trainer に渡す必要があります :

from cntk import distributed
...

learner = cntk.learner.momentum_sgd(...)    # create local learner
distributed_learner = cntk.distributed.block_momentum_distributed_learner(learner, block_size=block_size)
...
minibatch_source = MinibatchSource(...) 
...
trainer = Trainer(z, ce, pe, distributed_learner)
...
session = training_session(trainer=trainer, mb_source=minibatch_source, ...)
session.train()
...
distributed.Communicator.finalize()         # must be called to finalize MPI in case of successful distributed training

3. 分散トレーニング例題

分散トレーニングを有効にするだけであれば前章で説明したように非常に少ない変更ですみます。
しかし、より効率をあげるためには学習率やバッチサイズについて最適化を行なうことも必要です。

そのため、分散トレーニングを実装した以下のサンプル全体を簡単に眺めてみましょう :

MNIST_Complex_Training.py

このサンプルは MNIST を題材としたシンプルなものですが、以下のようなトレーニング時のオプションのショーケースとなっています。分散トレーニングもその一つとして実装されています :

チェックポインティング。
各ミニバッチ後にテスト評価。
学習率制御ベースの交差検証そしてユーザコード内でのトレーニングの早期停止。
MPI を使用したデータ並列分散トレーニング。

◆ さて、それでは具体的にコードにあたってみましょう。最初に必要なモジュールをインポートします :

from __future__ import print_function
import os
import cntk as C
import numpy as np
import scipy.sparse

特徴とラベルの次元を定義します :

# Define the task.
input_shape = (28, 28)  # MNIST digits are 28 x 28
num_classes = 10        # classify as one of 10 digits
model_path = os.path.join(os.path.dirname(os.path.abspath(__file__)), "Models/mnist.cmf")

scikit-learn を利用して MNIST データを取得します :

try:
    from sklearn import datasets, utils
    mnist = datasets.fetch_mldata("MNIST original")
    X, Y = mnist.data / 255.0, mnist.target
    X_train, X_test = X[:60000].reshape((-1,28,28)), X[60000:].reshape((-1,28,28))
    Y_train, Y_test = Y[:60000].astype(int), Y[60000:].astype(int)
except: # workaround if scikit-learn is not present
    import requests, io, gzip
    X_train, X_test = (np.fromstring(gzip.GzipFile(fileobj=io.BytesIO(requests.get('http://yann.lecun.com/exdb/mnist/' + name + '-images-idx3-ubyte.gz').content)).read()[16:], dtype=np.uint8).reshape((-1,28,28)).astype(np.float32) / 255.0 for name in ('train', 't10k'))
    Y_train, Y_test = (np.fromstring(gzip.GzipFile(fileobj=io.BytesIO(requests.get('http://yann.lecun.com/exdb/mnist/' + name + '-labels-idx1-ubyte.gz').content)).read()[8:], dtype=np.uint8).astype(int) for name in ('train', 't10k'))

訓練データをシャッフルしてから交差検証セットをスプリット・オフします。
特徴は float32 で、交差エントロピーは one-hot エンコードされたラベルを想定しています :

np.random.seed(0) # always use the same reordering, for reproducability
idx = np.random.permutation(len(X_train))
X_train, Y_train = X_train[idx], Y_train[idx]

X_train, X_cv = X_train[:54000], X_train[54000:]
Y_train, Y_cv = Y_train[:54000], Y_train[54000:]

Y_train, Y_cv, Y_test = (scipy.sparse.csr_matrix((np.ones(len(Y),np.float32), (range(len(Y)), Y)), shape=(len(Y), 10)) for Y in (Y_train, Y_cv, Y_test))
X_train, X_cv, X_test = (X.astype(np.float32) for X in (X_train, X_cv, X_test))

モデル関数を定義します。
モデル関数は入力データを予測にマップします (ここでは、(28, 28)-次元の入力 --> 10 スコア) :

with C.layers.default_options(activation=C.ops.relu, pad=False):
    model = C.layers.Sequential([
        C.layers.Convolution2D((5,5), num_filters=32, reduction_rank=0, pad=True), # reduction_rank=0 for B&W images
        C.layers.MaxPooling((2,2), strides=(2,2)),
        C.layers.Convolution2D((3,3), num_filters=48),
        C.layers.MaxPooling((2,2), strides=(2,2)),
        C.layers.Convolution2D((3,3), num_filters=64),
        C.layers.Dense(96),
        C.layers.Dropout(dropout_rate=0.5),
        C.layers.Dense(num_classes, activation=None) # no activation in final layer (softmax is done in criterion)
    ])

評価 (= criterion) 関数を定義します。評価関数は (入力ベクトル, ラベル) を損失関数とオプションのメトリクスにマップします。
損失関数はモデルパラメータをトレーニングするために使用され、損失関数として交差エントロピーを選択しています。
CNTK 交差エントロピーはラベルが one-hot 形式であることを想定しています。

与えられた入力型とともに宣言するために CNTK @Function.with_signature を使用します :

@C.Function.with_signature(C.layers.Tensor[input_shape], C.layers.SparseTensor[num_classes])
def criterion(data, label_one_hot):
    z = model(data)  # apply model. Computes a non-normalized log probability for every output class.
    loss   = C.cross_entropy_with_softmax(z, label_one_hot) # this applies softmax to z under the hood
    metric = C.classification_error(z, label_one_hot)
    return loss, metric

learner オブジェクトを作成します。learner は更新アルゴリズムを実装していて、ここでは momentum SGD を使用します。
このスクリプトはデータ並列トレーニングをサポートしているので、学習率は "サンプル毎" (UnitType.sample) に指定され、その値はミニバッチ・サイズで事前に既に除算されています。これはデータ並列トレーニングにおいてサンプル勾配毎の同じ寄与を維持しながら、データをサブセットに分割し、そしてまたミニバッチ・サイズを可能なところでは増大させることを可能にします :

epoch_size = len(X_train)
lr_per_sample    = 0.001
lr_schedule      = C.learning_rate_schedule(lr_per_sample, C.learners.UnitType.sample)
mm_time_constant = [0]*5 + [1024] # 5 epochs without momentum, then switch it on
mm_schedule      = C.learners.momentum_as_time_constant_schedule(mm_time_constant, epoch_size)

learner = C.learners.momentum_sgd(model.parameters, lr_schedule, mm_schedule)

次に trainer 用にコールバックを構成します。
本記事の主題ではないので細部は端折ります (必要であればコメントの翻訳を参照してください) が、これはこのサンプルが示す主要なポイントの一つです。
コールバックを通してロギング、チェックポインティング、学習率調整、早期停止、そして最終的なテストが利用できます :

# 各エポックの終わりに損失とメトリクスについて進捗ロギングするためのコールバック。
progress_writer = C.logging.ProgressPrinter()

# チェックポインティングのためのコールバック。これはモデルを 'epoch_size' サイズ・サンプル毎にセーブします。
# 利用可能な先行するチェックポイント・ファイルからトレーニングを開始するためには 'restore' を True に変更します。
checkpoint_callback_config = C.CheckpointConfig(model_path, epoch_size, restore=False)

# 交差検証のためのコールバック。
# 交差検証コールバックのメカニズムはユーザ自身の学習率調整と早期停止の実装を可能にします。
# 次は単純なコールバックを実装しています、
# これはメトリクスが少なくとも 5% relative 改善されない場合は学習率を半減します。
# 交差検証コールバックは 3*epoch_size サンプル毎に、i.e. 3rd epoch 毎だけにこれを呼び出すように configure されています。
prev_metric = 1 # metric from previous call to the callback. At very beginning, error rate is 100%.
def adjust_lr_callback(index, average_error, cv_num_samples, cv_num_minibatches):
    global prev_metric
    if (prev_metric - average_error) / prev_metric < 0.05: # relative gain must reduce metric by at least 5% rel
        learner.reset_learning_rate(C.learning_rate_schedule(learner.learning_rate() / 2, C.learners.UnitType.sample))
        if learner.learning_rate() < lr_per_sample / (2**7-0.1): # we are done after the 6-th LR cut
            print("Learning rate {} too small. Training complete.".format(learner.learning_rate()))
            return False # means we are done
        print("Improvement of metric from {:.3f} to {:.3f} insufficient. Halving learning rate to {}.".format(prev_metric, average_error, learner.learning_rate()))
    prev_metric = average_error
    return True # means continue
cv_callback_config = C.CrossValidationConfig((X_cv, Y_cv), 3*epoch_size, minibatch_size=256,
                                             callback=adjust_lr_callback, criterion=criterion)

# 最終的なモデルをテストするためのコールバック。
test_callback_config = C.TestConfig((X_test, Y_test), criterion=criterion)

分散トレーニングを構成します。これは 2 章で説明されたものです。
learner を distributed_learner オブジェクトでラップします :

learner = C.train.distributed.data_parallel_distributed_learner(learner)

分散トレーニングのためには、通信コストと GPU の未活用を最小化するためにミニバッチ・サイズを最大化しなければなりません。そのために、幾つかのエポックの後にミニバッチ数を増やす "スケジュール" を使用します。学習率を UnitType.sample として指定することにより、サンプル毎の寄与は学習率を整える必要なく同じスケールを維持します。

注意点として、この MNIST モデルについては、単純により大きなミニバッチ・サイズにすれば高速化します。何故ならば GPU をフルに活用するためにはモデルが小さ過ぎるからです。(従って、このモデルについては実はデータ並列トレーニングは必ずしも高速化に繋がることは期待できません。あくまで実装例の参考として考えるべきです) :

minibatch_size_schedule = C.minibatch_size_schedule([256]*6 + [512]*9 + [1024]*7 + [2048]*8 + [4096], epoch_size=epoch_size)

トレーニングとテストの実行です。コールバックにより、チェックポインティングや学習率調整等も併せて実行されます :

progress = criterion.train((X_train, Y_train), minibatch_size=minibatch_size_schedule,
                           max_epochs=50, parameter_learners=[learner],
                           callbacks=[progress_writer, checkpoint_callback_config, cv_callback_config, test_callback_config])

プロセスのスタッツを取得します :

final_loss    = progress.epoch_summaries[-1].loss
final_metric  = progress.epoch_summaries[-1].metric
final_samples = progress.epoch_summaries[-1].samples
test_metric   = progress.test_summary.metric

サンプルとして一つのミニバッチで予測を探求します。
評価のためには、ネットワーク出力を 0-1 の間にマップして確率に変換します。確率を得るためには softmax 関数を使用します :

@C.Function.with_signature(C.layers.Tensor[input_shape])
def get_probability(data):
    return C.softmax(model(data))

X_check, Y_check = X_test[0:10000:400].copy(), Y_test[0:10000:400] # a small subsample of 25 examples
result = get_probability(X_check)

print("Label    :", [label.todense().argmax() for label in Y_check])
print("Predicted:", [result[i,:].argmax() for i in range(len(result))])

例外なしに i..e 成功的にプロセスが終了したときは、MPI finalize を呼び出さなければなりません :

C.train.distributed.Communicator.finalize()

4. ベンチマーク

以下の２つのサンプルプログラムを利用して簡単なベンチーマーク・テストを実行してみます。
前者が基本的な畳み込み (ConvNet) モデルで、後者が ResNet-20 と ResNet-110 を実装しています :

手順としては、最初に Data-Parallel SGD を検証した後、Block-Momentum SGD を試してみます。

【注意点】
本章の検証結果はあくまで参考の一つとして考えてください。
本章で利用するモデルは CNN 系、データセットは CIFAR-10 のみで、分散処理を実行するにはやや軽めの題材です。
ベンチマークはモデルやデータセットに依存していることはもちろん、バッチサイズや (重みの) 初期値によっても大きく結果が違ってきます。

4-1. Data-Parallel SGD

(1) ノード数と 1-bit SGD の有効/無効による比較

最初にノード数 (1, 2, 4 ノード) と 1-bit SGD の有効/無効の違いによる、トレーニング (100 エポック) の実行時間と精度を比較してみます。特に ResNet-20 ではノード数の増加は顕著なパフォーマンス向上に繋がります。

ConvNet

サンプルの ConvNet では分散によるパフォーマンス向上は小さいです。
これはモデルが単純過ぎるために計算量の削減のメリットよりもオーバーヘッドの方が大きいためでしょう。
2 ノードの場合にはシングル・ノードの場合よりもパフォーマンスが落ちますが、4 ノードを使用すれば実行時間は短縮され、特に 1-bit SGD を有効にすれば 2 倍の速度が得られます。
4 ノードの場合、3 ポイント弱の精度の劣化が観測されます。この改善のためにはウォームスタートを利用してみます (後述)。

ノード数	1	2	2	4	4
GPU 総数	1	2	2	4	4
1-bit SGD	-	-	有効	-	有効
ウォームスタート	-	-	指定なし	-	指定なし
エポック数	100	100	100	100	100
実行時間	24m28.720s	44m49.391s	28m15.660s	20m47.812s	11m39.947s
速度比	1.0	0.55	0.87	1.18	2.10
エラー率	13.91%	14.20%	13.94%	16.70%	16.89%

ResNet-20

ResNet-20 の場合にはパフォーマンス向上は顕著です。
(ConvNet の場合とは逆に) 1-bit SGD は無効の方がパフォーマンスは良く、2 ノードで 1.8 倍、4 ノードで 3.8 倍もの速度向上が得られます。速度的には殆どオーバヘッドが見られません。
ウォームアップ指定なしでも精度の劣化も小さく、4 ノードでも 1.5 ポイント程度です。

ノード数	1	2	2	4	4
1-bit SGD	-	-	有効	-	有効
ウォームスタート	-	-	指定なし	-	指定なし
エポック数	100	100	100	100	100
実行時間	47m54.594s	26m5.013s	38m14.435s	12m37.295s	17m55.432s
速度比	1.0	1.84	1.25	3.80	2.67
エラー率	8.61%	8.53%	8.83%	10.03%	10.00%

(2) ウォームスタートのサンプル数による比較

次に、精度の劣化を改善する目的で、ウォームスタート時のサンプル数の違いで比較してみます。

ConvNet

ConvNet ではウォームスタートによる影響はほとんど見られません。
512 以上では実行時間が顕著に増大しますので、ウォームスタートは小さなセットにするべきでしょう。

ノード数	4	4	4	4	4	4	4
1-bit SGD	有効	有効	有効	有効	有効	有効	有効
ウォームスタート	指定なし	32	64	128	256	512	1024
エポック数	50	50	50	50	50	50	50
実行時間	5m13.812s	5m9.995s	5m9.849s	5m12.646s	5m9.278s	9m54.309s	9m6.252s
エラー率	18.45%	18.95%	17.05%	17.58%	18.52%	17.55%	19.04%

ResNet-20

ResNet-20 では最大で 3 ポイントの改善が見られました。
実行時間は 512 までは殆ど変わりませんが、1024 以上で増大します。

ノード数	4	4	4	4	4	4	4
1-bit SGD	有効	有効	有効	有効	有効	有効	有効
ウォームスタート	指定なし	32	64	128	256	512	1024
エポック数	50	50	50	50	50	50	50
実行時間	8m58.571s	8m57.460s	8m58.672s	8m56.593s	8m58.817s	8m56.567s	10m51.543s
エラー率	17.94%	15.21%	20.17%	14.96%	15.21%	16.49%	16.84%

(3) ResNet-110 (25 エポック)

これまでの検証結果を踏まえた上で、ResNet-110 モデルについて 25 エポックで検証してみました :

(これは予想がつきますが) ResNet-20 と似た傾向になり、2 ノードでも 4 ノードでも速度が向上します。
1-bit SGD が無効の場合の方が速度の向上が大きいです。
但し、精度は 1-bit SGD の方が良く、これはウォームスタートの効果でしょう。
ウォームスタートのサイズは 128 くらいが丁度良いかもしれません。1024 では時間の増大はともかくも精度も落ちました。

ノード数	1	2	2	4	4	4
1-bit SGD	-	-	有効	-	有効	有効
ウォームスタート	-	-	128	-	128	1024
実行時間	60m35.883s	31m41.753s	39m51.486s	16m36.695s	20m54.765s	27m9.541s
速度比	1.0	1.91	1.52	3.65	2.90	2.23
エラー率	18.14%	19.17%	16.36%	17.09%	15.96%	18.54%

(4) BN-Inception (25 エポック)

ついでに BN Inception モデルについても試しておきました :

4 ノードで大幅な速度向上が見込めます。このケースでも 1-bit SGD が無効の場合の方が速度の向上が大きいです。
しかしながら精度は 4 ノードでは大きく劣化します。(何度か試してみましたが、この傾向は変わりませんでした。)
(この表には掲載していませんが、) ウォームスタートの利用も精度的には芳しくはなく、モデルによっては分散処理による精度劣化は避けられないようです。
但し、次章で明らかになるように、速度を頼みとしてトレーニングするエポック数を増やせば十分な精度が得られました。

ノード数	1	2	2	4	4
1-bit SGD	-	-	有効	-	有効
実行時間	62m52.972s	32m54.443s	41m45.954s	17m32.630s	21m32.795s
速度比	1.0	1.91	1.51	3.58	2.92
エラー率	16.59%	15.80%	15.11%	21.32%	43.58%

4-2 Block-Momentum SGD

Block-Momentum SGD は速度は非常に上がるのですが、一方で精度の上がりは悪くなりますので、Data-Parallel SGD との比較は難しいです。
そのため、節を分けて記載しています。

(1) ブロックサイズ

ブロックサイズが小さいほど、i.e. ブロック数が大きいほど、精度はあがりますが実行時間がかかります。
逆に、ブロックサイズが大きいほど、精度は下がりますが実行時間は短縮できます。

ConvNet (batch-size : 256)

ノード数	4	4	4	4	4	4	4	4
block size	100	250	500	1000	2000	3000	5000	10000
エポック数	100	100	100	100	100	100	100	100
実行時間	10m6.895s	8m3.065s	8m4.348s	7m59.413s	6m46.328s	6m15.659s	5m56.688s	5m38.819s
エラー率	25.18%	26.80%	24.19%	27.78%	25.45%	25.35%	23.60%	24.14%

ConvNet (batch-size : 200)

(単なる思いつきですが、) バッチサイズをブロックサイズの約数にしてみたら精度が改善されました。

ノード数	4	4	4	4
block size	1000	2000	4000	10000
エポック数	100	100	100	100
実行時間	7m29.106s	6m55.156s	6m25.176s	5m56.229s
エラー率	22.61%	22.19%	21.22%	22.45%

ResNet-20

ノード数	4	4	4	4
block size	250	500	1000	2000
エポック数	100	100	100	100
実行時間	10m5.230s	10m4.798s	10m3.853s	10m4.792s
エラー率	25.67%	25.22%	31.40%	34.23%

(2) ウォームスタートのサンプル数による比較

次に、ブロックサイズを固定して、ウォームスタートのサイズを違えて比較してみましたが、これについては明確な傾向は出ませんでした。

ConvNet

ノード数	4	4	4	4
block size	2000	2000	2000	2000
ウォームスタート	指定なし	50	100	200
実行時間	6m55.156s	6m54.482s	6m48.213s	6m52.531s
エラー率	22.19%	21.50%	26.66%	21.14%

ResNet-20

ノード数	4	4	4	4
block size	500	500	500	500
ウォームスタート	指定なし	50	100	200
実行時間	10m4.798s	10m4.878s	10m5.846s	10m2.207s
エラー率	25.22%	26.77%	24.19%	25.13%

5. CIFAR-10 分散トレーニングの結果

前回の記事 :

CNTK 2.2 Python API 解説 (1) - CIFAR-10 CNN モデルの改良 / VGG, ResNet の実装

で、比較的簡単なモデルで CIFAR-10 をトレーニングして精度を確認してみました :

モデル	VGG-9	ResNet (簡易版)	基本モデル + BN
エポック数	200	250	150
実行時間	66min 21s	126min 22s	15min 48s
テスト精度	83.3 %	81.9 %	82.1 %

そして今回はより複雑なモデル: BN Inception や ResNet-110 を分散トレーニングすることによって以下のテスト精度を得ました :

|アルゴリズム|BN Inception|BN Inception|ResNet-110|ResNet-20|ResNet-20|ResNet-20|
|:--|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|分散アルゴリズム|Data-Parallel|Data-Parallel|Data-Parallel|Data-Parallel|Block-Momentum|Block-Momentum|
|ノード数|4|4|4|4|4|4|
|1-bit SGD|-|-|有効|有効|-|-|
|ブロックサイズ|-|-|-|-|500|500|
|ウォームスタート|-|-|128|128|100|100|
|エポック数|100|200|100|500|1000|500|
|バッチサイズ|64|128|128|default|default|default|
|実行時間|234m48.645s|137m44.898s|80m44.518s|87m30.971s|98m26.524s|49m14.955s|
|エラー率|5.96%|8.63%|8.47%|9.90%|14.12%|14.23%|
|テスト精度|94.04%|91.37%|91.53%|90.10%|85.88%|85.77%|

BN Inception ではテスト精度 94.04 % に達しており、これはなかなか良い数字です。ResNet-110, ResNet-20 も 90 % を超えました。

【補足】
今回は分散トレーニング自身の性能を見ることが主目的ですので、個々のモデルを同一の条件で十分な時間をかけてトレーニングしたわけではありません。例えば、ResNet-110 は明らかにトレーニング時間が不足しています。
従って、得られたテスト精度はモデルの優劣を示すものではありませんのでご注意ください。

以上

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up