【非専門家向け】BERT - chiVe / chiTra 利活用に向けて Part3.

本記事では後半にword2vecとBERTの分散表現の特徴の違いを見るためのコードがありますが、これらはこちらのGoogle Colabから実際に試すことができます。

chiVe, chiTra の利用を考えているが、そもそも単語分散表現や事前学習済みモデルとは？という方向けに、単語分散表現や事前学習モデルのイメージをつけていただくシリーズのPart3です。

Part1で、計算機で単語の "意味" を扱うイメージをつけるために、one-hotベクトル と 共起頻度行列 を取り上げました。
共起頻度行列によって単語の "意味" を捉えられそうだが、語彙数分の次元が必要になるなど実利用の上では課題がありそうだというお話をしました。

Part2では、word2vec を取り上げ、共起頻度行列において問題として挙げた次元数の問題や新語への対応の煩雑さの解決のお話や、学習方法や多義性を捉えられないなどの実用上の課題のお話をしました。

Part3では、chiTra のモデルのベースである BERT を取り上げます。

Part1：単語の "意味" を計算機で扱うイメージをつける
Part2：word2vec

BERT

BERTは2018年にDevlinらによって提案されました（元論文：BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding）。
理論の詳細に関してはより詳しい解説記事や元論文を追っていただくことにして、本記事ではイメージをつけていただくことを目標とします。

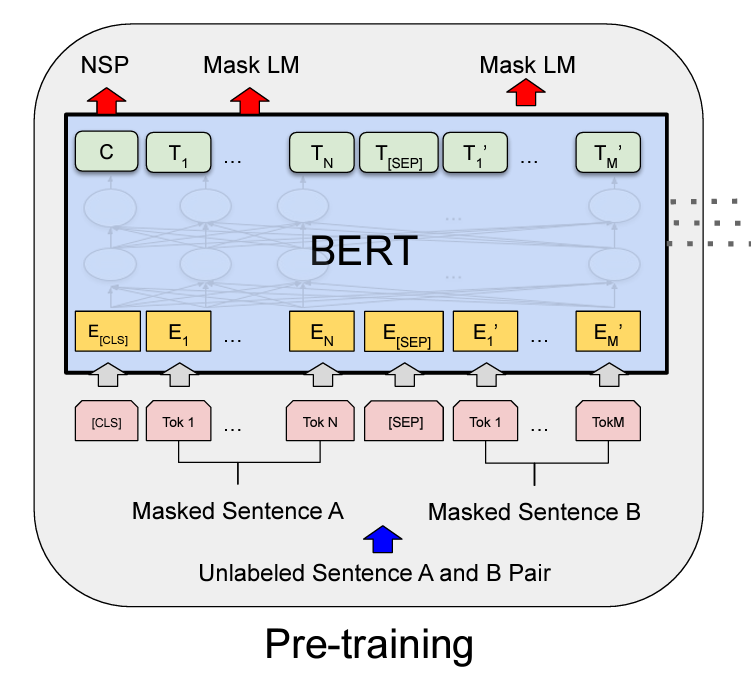
word2vecでは、学習において周辺語から対象語を推定する（CBOWの場合。skip-gramは対象語から周辺語を推定する）タスクを解く過程で単語のベクトルを獲得しますが、BERTでは、masked language model (Mask LM, MLM) と next sentence prediction (NSP) という2つのタスクを解く過程で学習を行います。（図は元論文から拝借）

• masked language model (Mask LM, MLM)
  BERTの入力には、2つの文を与えます（上図の Unlabeled Sentence A and B Pair）。その際、文中の一部のトークンを隠し（mask し）て（上図の Masked Sentence AとMasked Sentence B）、そのトークンが何かを予測するタスクを解かせます。
  これにより、その文脈における単語の意味を獲得することを期待します。
• next sentence prediction (NSP)
  入力された2文A, Bがコーパス上での連続した2文か否かを予測するタスクを解かせます。
  質問応答や含意関係認識など、2文間の関係を捉えることが重要な下流タスクが多く存在しますが、MLMだけではそのような文間の関係を捉えることはできません。NSPにより文間の関係を学習することを期待します。

BERTのすごさ

BERTは2018年に登場し、現在の深層学習の流れに大きな影響を与えました。
その大きな理由の一つとして挙げられるのが、上記2つの学習（これを事前学習; Pre-training と言います。）を行ったモデルに対し、下流タスクのデータで微調整（これをFine-Tuning と言います。）をするだけで、様々なタスクで当時の最高性能を達成したことです。

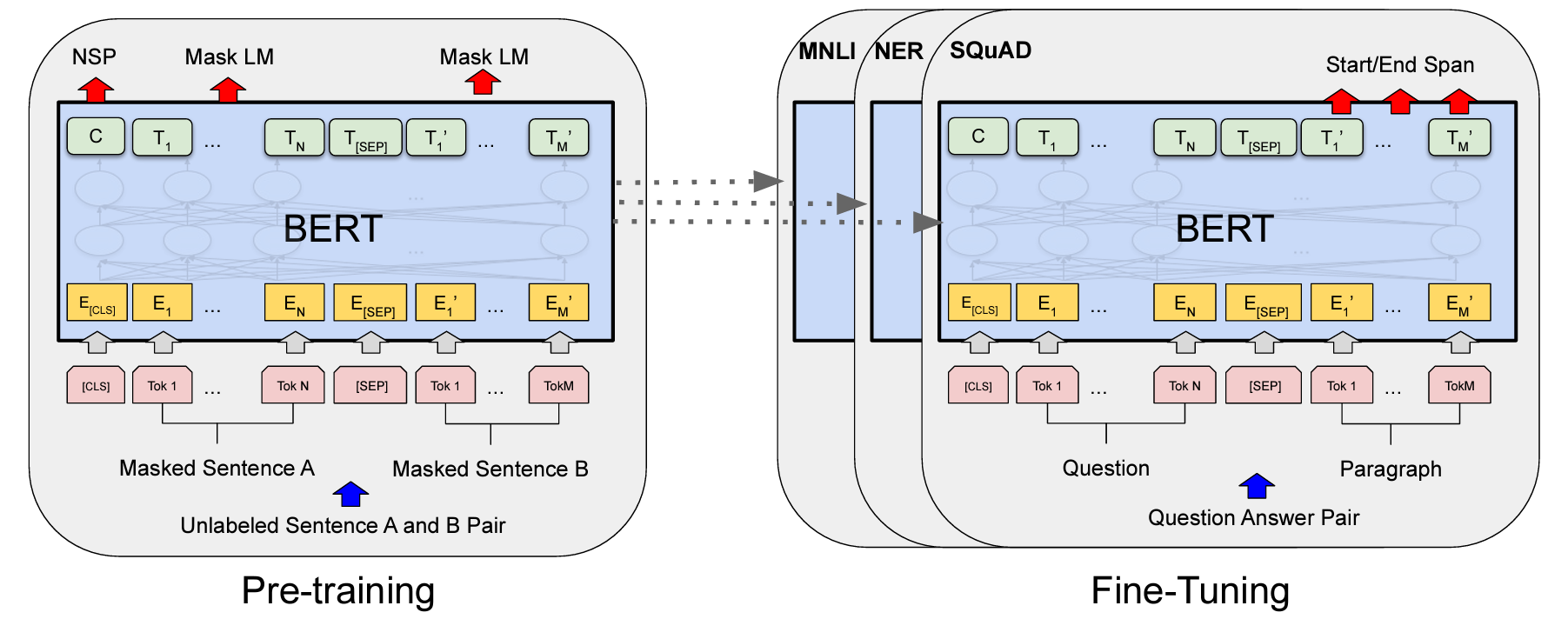
図の左側が事前学習（Pre-training）で、上記のMLMとNSPを行います。事前学習にはある程度大きな規模の言語リソースと計算機リソースが必要です。
具体的には、提案論文で構築されたモデル（BERT-base）は、BooksCorpusと英語wikipediaの合わせて33億語のコーパスを使い、当時のCloud-TPU 4つ（TPU 16チップ）で4日間の学習を行っています。
このような規模の事前学習を行うモデルを誰もが簡単に作れるものではありません。ただ、事前学習が済んでしまえば、Fine-Tuning（図の右側）はそれほど重い学習が必要なく（論文内では、Cloud-TPU 1個で1時間、GPU 1個で2~3時間程度と報告）、それでいて高い精度が出ることが広く受け入れられた要因かと思います。

事前学習済みモデルは、ある程度大きな計算機リソースを持つ研究機関や企業が公開していることが多く、現在では日本語でも様々なモデルが公開されています。利用者はその事前学習済みモデルに対し自前のデータと下流タスクを用意し、Fine-Tuningを行い利用するのが一般的です。

chiTra もそんな事前学習済みモデルの一つです。
chiTraを利用して実際にFine-Tuningをする方法は、こちら（chiTra事前学習モデルを使って評判分析を行う）などで解説されていますので、興味がある方はそちらも参考にしてください。

単語分散表現 ↔ 事前学習済みモデル

前回と今回で、単語分散表現と事前学習済みモデルそれぞれのイメージをつけることを目的とした解説を行ってきました。
では、それぞれの違いは何でしょうか？どのような局面でどちらを利用するとよいでしょうか？

静的 ↔ 動的

単語分散表現も事前学習済みモデルもそれぞれ単語（トークン）にベクトルが付与されますが、利用者目線での大きな違いは 単語分散表現のベクトルは静的、事前学習済みモデルのベクトルは動的と言うことができると思います。

単語分散表現は静的

前回、単語分散表現の課題として多義性を考慮できないというお話をしました。
具体例を以下に再掲します。学習コーパス内でよく出現する意味が強いベクトルとなり、多義性を捉えることはできません。

python

# モデルのロード
import gensim
vectors = gensim.models.KeyedVectors.load("path/to/chive-1.2-mc90_gensim/chive-1.2-mc90.kv")

# targetの語の近傍を検索
target = "マック"
vectors.most_similar(target)

# [('マクド', 0.7141627073287964),
# ('マクドナルド', 0.6885151863098145),
# ('モスバーガー', 0.6016820669174194),
# ('ロッテリア', 0.5896010994911194),
# ('MAC', 0.5882739424705505),
# ('ハンバーガー', 0.5843257308006287),
# ('バーガー', 0.5826560258865356),
# ('ミスド', 0.5790222883224487),
# ('フレッシュネス', 0.5472289323806763),
# ('デニーズ', 0.5406960844993591)]

事前学習済みモデルは動的

一方、事前学習済みモデルは出現する文脈により同じ表層でもベクトルが変化します。
これを垣間見える実験をしてみます。（以下は、BERT Word Embeddings Tutorial の内容を参考にchiTraに対して適用したものです。）

準備として、chiTraモデルをロードします。

from sudachitra.tokenization_bert_sudachipy import BertSudachipyTokenizer
from transformers import BertModel

tokenizer = BertSudachipyTokenizer.from_pretrained('path/to/chiTra-1.0')
model = BertModel.from_pretrained('path/to/chiTra-1.0', output_hidden_states=True)

3つの文を考えます。

text = "お腹が空いたのでマックでハンバーガーを食べた。" \
       "マックのポテトは揚げたてがおいしい。" \
       "Appleから発売された新型のマックPCを買った。"
marked_text = "[CLS] " + text + " [SEP]"
target = "マック"

3文それぞれに "マック" という文字列が含まれていますが、1文目と2文目の "マック" は "マクドナルド"、3文目の "マック" はApple製品という想定です。

この文をトークナイズし、各トークンの埋め込みを得ます。
（結果のみ知りたい方は、以下のコードはスキップして先に進んでOKです。）

import torch

# テキストをトークンに分割
tokenized_text = tokenizer.tokenize(marked_text)
# トークン文字列を語彙インデックスにマッピング
indexed_tokens = tokenizer.convert_tokens_to_ids(tokenized_text)
# トークン文字列にsegment ID: 1 を付与。
#（BERTではテキストをペアとして入力することを期待し、各トークンがどちらのテキスト（0, 1）
# に属するのかを指定する必要があります。1テキストの入力では 1 を指定します。）
segments_ids = [1] * len(tokenized_text)

# 入力を PyTorch テンソルに変換
tokens_tensor = torch.tensor([indexed_tokens])
segments_tensors = torch.tensor([segments_ids])

with torch.no_grad():
    # BERTモデルに入力
    outputs = model(tokens_tensor, segments_tensors)
    # 全レイヤーの隠れ状態を取得
    # (今回の設定では、outputs の3番目（index: 2）に全レイヤーの隠れ状態の情報が保存されています。)
    hidden_states = outputs[2]

# 今回の目的に合わせ、テンソルを操作
#（操作の意図は、今回参考にしているチュートリアル: 
# https://mccormickml.com/2019/05/14/BERT-word-embeddings-tutorial/#32-understanding-the-output 
# を参照してください。）
token_embeddings = torch.stack(hidden_states, dim=0)
token_embeddings = torch.squeeze(token_embeddings, dim=1)
token_embeddings = token_embeddings.permute(1,0,2)

token_vecs_sum = []
for token in token_embeddings:
    # 上（出力に近い側）4層のベクトルの和を取り、各トークンのembeddingとする。
    # 4層の意図は、今回参考にしているチュートリアル: 
    # https://mccormickml.com/2019/05/14/BERT-word-embeddings-tutorial/#35-pooling-strategy--layer-choice 
    # を参照してください（その他さまざまなパターンの検討がされたことが共有されています）。
    sum_vec = torch.sum(token[-4:], dim=0)
    token_vecs_sum.append(sum_vec)

まず、トークナイズした結果を見てみましょう。サブワートという単位で分割されています。

print(marked_text)
for i, token_str in enumerate(tokenized_text):
  print (i, token_str)

# [CLS] お腹が空いたのでマックでハンバーガーを食べた。マックのポテトは揚げたてがおいしい。Appleから発売された新型のマックPCを買った。 [SEP]
# 0 [CLS]
# 1 御
# 2 ##腹
# 3 が
# 4 空い
# 5 た
# 6 の
# 7 で
# 8 マック
# 9 で
# 10 ハン
# 11 ##バー
# 12 ##ガー
# 13 を
# 14 食べ
# 15 た
# 16 。
# 17 マック
# 18 の
# 19 ポ
# 20 ##テ
# 21 ##ト
# 22 は
# 23 揚げ
# 24 ##立て
# 25 が
# 26 おい
# 27 ##しい
# 28 。
# 29 アップル
# 30 から
# 31 発売
# 32 さ
# 33 れ
# 34 た
# 35 新型
# 36 の
# 37 マック
# 38 PC
# 39 を
# 40 買っ
# 41 た
# 42 。
# 43 [SEP]

では、このテキスト内の3つの "マック" のベクトルの中身を見てみましょう。
すると、それぞれの "マック" のベクトルが異なっていることがわかります。

target_indices = [n for n, v in enumerate(tokenized_text) if v == target]
print(f'text中での "{target}" のindex: {target_indices}')
print('-----')
print(f'それぞれの文における "{target}" ベクトルの先頭5次元.')
for index in target_indices:
  print(f'{index}番目のトークン "{target}": ', str(token_vecs_sum[index][:5]))

# text中での "マック" のindex: [8, 17, 37]
# -----
# それぞれの文における "マック" ベクトルの先頭5次元.
# 8番目のトークン "マック":  tensor([-0.9744, -1.8931, -0.1455, -1.6762,  8.5918])
# 17番目のトークン "マック":  tensor([-0.5120, -0.0783, -1.8962, -2.7612,  8.5514])
# 37番目のトークン "マック":  tensor([ 3.9718, -0.8314,  0.6743,  0.9934,  2.3082])

最後に、それぞれのベクトル間の類似度を測ってみましょう。
すると、8番目（1文目）と17番目（2文目）のトークン "マック" の間の類似度（0.80）の方が、8番目（1文目）と37番目（3文目）のトークン "マック" の間の類似度（0.63）よりも高いことが見てとれます。
このように、BERTでは同じ表層の文字列でも文脈により 動的 にベクトルが変化することがわかりました。

from scipy.spatial.distance import cosine

same_target = 1 - cosine(token_vecs_sum[target_indices[0]], token_vecs_sum[target_indices[1]])
diff_target = 1 - cosine(token_vecs_sum[target_indices[0]], token_vecs_sum[target_indices[2]])

print(f'{target_indices[0]}番目のトークン と {target_indices[1]}番目のトークン の "{target}" の間の類似度:  {same_target:.2f}')
print(f'{target_indices[0]}番目のトークン と {target_indices[2]}番目のトークン の "{target}" の間の類似度:  {diff_target:.2f}')

# 8番目のトークン と 17番目のトークン の "マック" の間の類似度:  0.80
# 8番目のトークン と 37番目のトークン の "マック" の間の類似度:  0.63

利用局面の違い

ビジネス利用の観点でのそれぞれのメリット、デメリットを大雑把にまとめると以下のようになると思います。

• 単語分散表現
  • メリット : 比較的低資源、短時間で動かせる
  • デメリット : BERTほどの精度は期待できないタスクが多い
• 事前学習済みモデル
  • メリット : 多くのタスクで精度面で圧倒的優位
  • デメリット : それなりの計算資源、実行時間が必要

精度と計算資源のトレードオフと言えると思います。
低コストで軽量に動かしたい場合は単語分散表現、計算資源が豊富で高精度を追い求めたい場合は事前学習済みモデルの利用を検討するとよいでしょう。

まとめ

「chiVe / chiTra 利活用に向けて」の Part3 として、BERTを紹介しました。
文脈に応じてベクトルが変化し、ファインチューニングによりさまざまなタスクで高精度が出せることがわかりました。

ワークスでは、単語分散表現として chiVe、事前学習済みモデルとして chiTra を公開しています。
今回のシリーズでなんとなくでもイメージがつきましたら、ぜひ触ってみてください！